Sistemas de equações diferenciais com atrasos fixos - SIRS: mudanças entre as edições
m (Jhordan moveu a página Sistemas de equações diferenciais com atrasos fixos - SARS para Sistemas de equações diferenciais com atrasos fixos - SIRS: Erro de digitação) |
Sem resumo de edição |
||
| (3 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[Análise de estabilidade de equações diferenciais lineares atrasadas | Equações diferenciais com atrasos]] |[[ | {{Ecologia| [[Análise de estabilidade de equações diferenciais lineares atrasadas | Exemplo: equação diferencial com retardo ]] |[[Simulação e modelo de campo médio]]}} | ||
=== O sistema === | |||
O exemplo a ser considerado é da biologia matemática, muitas ferramentas matemáticas utilizado na dinâmica de populações encontra-se também na dinâmica de epidemias. O objetivo deste tópico não é se aprofundar na modelagem em si, mas a utilizar como motivação para compreender melhor os sistemas de equações diferenciais com atraso baseado no artigo "''Oscillations in SIRS model with distributed delays''". | |||
Uma doença do tipo SIRS é caracterizada por um tempo de infecção <math display="inline">\tau_{i}</math> e um tempo de imunidade <math display="inline">\tau_{r}</math>. Isto é, um indivíduo que se infecte em um tempo <math display="inline">t</math> vai deterministicamente se recuperar em um tempo <math display="inline">t+\tau_{i}</math>, tornando-se temporariamente imune por um tempo <math display="inline">\tau_{r}</math>. Então no instante <math display="inline">t+\tau_{i}+\tau_{r}\equiv t+\tau_{0}</math> perde a imunidade tornando-se suscetível novamente. Este sistema pode ser representado por um conjunto de equações para a fração de população infecciosa (e infectada) <math display="inline">i\left(t\right)</math> e suscetível <math display="inline">s\left(t\right)</math>: | |||
<math display="block">\dot{s}\left(t\right)=-\beta s\left(t\right)i\left(t\right)+\beta s\left(t-\tau_{0}\right)i\left(t-\tau_{0}\right)</math> | |||
<math display="block">\dot{i}\left(t\right)=\beta s\left(t\right)i\left(t\right)-\beta s\left(t-\tau_{i}\right)i\left(t-\tau_{i}\right)</math> | |||
Onde <math display="inline">\beta</math> é a taxa de contágio por indivíduo. A fração da subpopulação em recuperação (imune) é dada por <math display="inline">r\left(t\right)=1-s\left(t\right)-i\left(t\right)</math>. O primeiro termos em ambas as equações representa o contágio dos suscetíveis pelos infecciosos, daqui em diante muitas vezes será referido como: <math display="inline">c\left(t\right)=\beta s\left(t\right)i\left(t\right)</math>. Os segundos termos representam a recuperação ou a perda de imunidade após <math display="inline">\tau_{i}</math> e <math display="inline">\tau_{0}</math> decorrido desde a infecção, respectivamente. Isto é: | |||
<math display="block">\dot{s}\left(t\right)=-c\left(t\right)+c\left(t-\tau_{0}\right)</math> | |||
<math display="block">\dot{i}\left(t\right)=c\left(t\right)-c\left(t-\tau_{i}\right)</math> | |||
Em outras palavras, uma fração <math display="inline">c\left(t\right)</math> se contagia no instante <math display="inline">t</math>, no instante <math display="inline">t+\tau_{i}</math> ela se recupera, diminuindo os infecciosos. No instante <math display="inline">t+\tau_{i}+\tau_{r}</math> ela perde a imunidade, aumentando a quantidade de suscetíveis. Estas equações exigem condições iniciais, matematicamente usualmente se fornece funções arbitrárias <math display="inline">s\left(t\right)</math> e <math display="inline">i\left(t\right)</math> no intervalo <math display="inline">\left[-\tau_{0},0\right]</math>. Porém de um ponto de vista epidemiológico, é razoável prover condições iniciais em <math display="inline">t=0</math> e dinâmicas complementares nos intervalos <math display="inline">\left[0,\tau_{i}\right)</math> e <math display="inline">\left[\tau_{i},\tau_{0}\right)</math> . | |||
*<math display="inline">\left[0,\tau_{i}\right)\rightarrow</math> somente contágio local. Utiliza-se as equações apenas com os primeiros termos, sem atraso. | |||
*<math display="inline">\left[\tau_{i},\tau_{0}\right)\rightarrow</math>Transição do estágio de infeccioso para em recuperação, ou seja, retira-se apenas o segundo termo na equação da dinâmica dos suscetíveis. | |||
E com as condições iniciais: | |||
<math display="block">s\left(0\right)=1-i_{0},i\left(0\right)=i_{0},r\left(0\right)=0</math> | |||
=== Ponto de equilíbrio === | |||
Para análise dos pontos de equilíbrio uma representação integral é uma forma melhor forma de representar o sistema, pois se fizermos algo análogo ao que foi feito em [[Análise de estabilidade de equações diferenciais lineares atrasadas | Equações diferenciais com atrasos]], não será possível obter nenhuma informação sobre o ponto de equilíbrio, pois aparentemente qualquer par de valores poderia representar um ponto de equilíbrio. Para a dinâmica dos infecciosos é proposto então: | |||
<math display="block">i\left(t\right)=c_{1}+\int_{t-\tau_{i}}^{t}c\left(u\right)du</math> | |||
A interpretação é direta, integra-se sobre sobre todos os indivíduos que se contagiaram entre o tempo <math display="inline">t-\tau_{i}</math> e <math display="inline">t</math>. Estes serão os infecciosos no instante <math display="inline">t</math>, uma vez que todos infectados anteriormente a este tempo já estarão recuperados. A constante de integração <math display="inline">c_{1}</math> a princípio é arbitrária, mas espera-se que <math display="inline">c_{1}=0</math> pois não deve haver outras fontes de infecções adicionais. Complementariamente: | |||
<math display="block">1-r\left(t\right)=c_{2}-\int_{t-\tau_{0}}^{t-\tau_{i}}c\left(u\right)du</math> | |||
Pelo lado esquerdo, pode-se perceber ver que isto se refere a população que não está se recuperando, isto é <math display="inline">1-r\left(t\right)=s\left(t\right)+i\left(t\right)</math>, ou seja, os infectados e suscetíveis. A integral cobre os contágios que ocorreram durante <math display="inline">\tau_{r}</math> anterior. Desta forma, esta integral fornece o número de pessoas que estão no período de recuperação, logo é razoável supor que <math display="inline">c_{2}=1</math> uma vez que também não há outras fontes de pessoas em recuperação. Para um estado de equilíbrio então que a fração de contagiados em um instante <math>t</math> qualquer é constante, pode-se escrever <math display="inline">c\left(u\right)=c_{0}</math> . Para <math display="inline">i\left(t_{0}\right)</math>: | |||
<math display="block">\begin{align} | |||
i\left(t_{0}\right) & =c_{0}\int_{t_{0}-\tau_{i}}^{t_{0}}du\\ | |||
& =c_{0}\left(t_{0}-t_{0}+\tau_{i}\right)\\ | |||
& =c_{0}\tau_{i}\end{align}</math> | |||
E para <math display="inline">s\left(t_0\right)</math>, de maneira análoga: | |||
<math display="block">\begin{align} | |||
s\left(t_{0}\right) & =1-\int_{t_{0}-\tau_{0}}^{t_{0}-\tau_{i}}c\left(u\right)du-i\left(t_{0}\right)\\ | |||
& =1-c_{0}\int_{t_{0}-\tau_{0}}^{t_{0}-\tau_{i}}du-c_{0}\tau_{i}\\ | |||
& =1-c_{0}\left(t_{0}-\tau_{i}-t_{0}+\tau_{0}\right)-c_{0}\tau_{i}\\ | |||
& =1-c_{0}\left(-\tau_{i}+\tau_{i}+\tau_{r}\right)-c_{0}\tau_{i}\\ | |||
& =1-c_{0}\tau_{r}-c_{0}\tau_{i}\\ | |||
& =1-c_{0}\left(\tau_{r}+\tau_{i}\right)\\ | |||
& =1-c_{0}\tau_{0}\end{align}</math> | |||
Uma vez que <math>s\left(t\right)=1-r\left(t\right)-i\left(t\right)</math>. Lembrando que <math display="inline">c\left(t\right)=\beta s\left(t\right)i\left(t\right)</math> , então no estado de equilíbrio <math display="inline">c_{0}=\beta s\left(t_{0}\right)i\left(t_{0}\right)</math>, denotando os pontos de equilíbrio apenas como <math display="inline">s\left(t_{0}\right)=s^{*}</math> e <math display="inline">i\left(t_{0}\right)=i^{*}</math>, obtém-se do primeiro resultado: | |||
<math display="block">\begin{align} | |||
i^{*} & =\beta s^{*}i^{*}\tau_{i}\\ | |||
s^{*} & =\frac{1}{\beta\tau_{i}}\end{align}</math> | |||
E do segundo: | |||
<math display="block">\begin{align} | |||
1 & =1-\beta s^{*}i^{*}\tau_{0}\\ | |||
1 & =\frac{1}{s^{*}}-\beta i^{*}\tau_{0}\\ | |||
\beta i^{*}\tau_{0} & =\beta\tau_{i}-1\\ | |||
i^{*} & =\frac{\beta\tau_{i}-1}{\beta\tau_{0}}\end{align}</math> | |||
Assim o ponto de equilíbrio é: <math display="inline">\left(s^{*},i^{*}\right)=\left(\frac{1}{\beta\tau_{i}},\frac{\beta\tau_{i}-1}{\beta\tau_{0}}\right)</math>. | |||
==== Validade da aproximação e sistema de equações sem atraso ==== | |||
Uma atenção especial deve ser dada a consideração de que <math display="inline">c_{1}=0</math> quando foi proposto a equação integral para <math display="inline">i\left(t\right)</math>. A formulação matemática do modelo sem atraso é usualmente escrito como: | |||
<math display="block">\begin{align} | |||
\frac{ds\left(t\right)}{dt}= & -\beta s\left(t\right)i\left(t\right)+\frac{r\left(r\right)}{\tau_{r}}\\ | |||
\frac{di\left(t\right)}{dt}= & \beta s\left(t\right)i\left(t\right)-\frac{i\left(r\right)}{\tau_{i}}\\ | |||
\frac{dr\left(t\right)}{dt}= & \frac{i\left(r\right)}{\tau_{i}}-\frac{r\left(r\right)}{\tau_{r}}\end{align}</math> | |||
Integrando a equação da dinâmica de <math display="inline">i\left(t\right)</math> do sistema sem atraso, de <math display="inline">t^{*}-\tau_{i}</math> a <math display="inline">t^{*}</math>, obtém-se: | |||
<math display="block">\begin{align} | |||
\frac{di\left(t\right)}{dt} & =\beta s\left(t\right)i\left(t\right)-\frac{i\left(t\right)}{\tau_{i}}\\ | |||
\int_{i\left(t^{*}-\tau_{i}\right)}^{i\left(t^{*}\right)}di & =\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-\frac{1}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}i\left(t\right)dt\\ | |||
i\left(t^{*}\right) & =\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau_{i}\right)-\frac{1}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}i\left(t\right)dt\right]{eq:tri}\end{align}</math> | |||
Considerando no equilíbrio que <math display="inline">i\left(t^{*}\right)=i\left(t^{*}-\tau_{i}\right)</math>: | |||
<math display="block">\begin{align} | |||
0 & =\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-\frac{i^{*}}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}i\left(t\right)dt\\ | |||
\frac{i^{*}}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}i\left(t\right)dt & =\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt\end{align}</math> | |||
Sendo que no equilíbrio os valores são constantes <math display="inline">i\left(t\right)=i^{*}</math> e <math display="inline">s\left(t\right)=s^{*}</math>: | |||
<math display="block">\begin{align} | |||
\frac{i^{*}}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}dt & =\beta s^{*}i^{*}\int_{t^{*}-\tau_{i}}^{t^{*}}dt\\ | |||
i^{*} & =\beta s^{*}i^{*}\tau_{i}{eq:siete}\end{align}</math> | |||
De onde é possível obter também o mesmo ponto de equilíbrio obtido anteriormente: | |||
<math display="block">\begin{align} | |||
s^{*} & =\frac{1}{\beta\tau_{i}}\end{align}</math> | |||
Outra formar de comparar as equações, é que para obter versão integral apresentada para <math display="inline">i\left(t\right)</math> a partir de:: | |||
<math display="block">i\left(t^{*}\right)=\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau_{i}\right)-\frac{1}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}i\left(t\right)dt\right]</math> | |||
É é necessário que o termo entre colchete seja zerado. Isto é, considerando que no equilíbrio <math display="inline">i\left(t^{*}-\tau_{i}\right)</math> e <math display="inline">i\left(t^{*}-\tau_{i}\right)</math> sejam constantes: | |||
<math display="block">\begin{align} | |||
i\left(t^{*}-\tau_{i}\right) & =\frac{1}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}i\left(t\right)dt\\ | |||
i\left(t^{*}-\tau_{i}\right) & =i\left(t^{*}\right)\end{align}</math> | |||
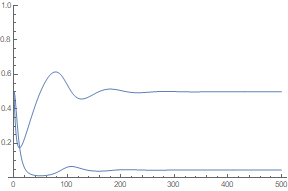
Desta forma a condição imposta anteriormente é recuperada. Agora percebe-se que o ponto de equilíbrio é independente das condições iniciais, depende apenas dos parâmetros escolhidos <math display="inline">\beta,\tau_{i}</math> e <math display="inline">\tau_{r}</math>. Por exemplo, resolvendo numericamente o sistema de equações diferenciais proposto, com os parâmetros <math display="inline">\beta=0.4</math>, <math display="inline">\tau_{i}=5</math> e <math display="inline">\tau_{r}=50</math>, e condições iniciais <math display="inline">\left(s_{0},i_{0}\right)=\left(0.5,0.5\right)</math>, o sistema atinge o equilíbrio precisamente nos pontos calculados. | |||
[[Ficheiro:sem_atraso.png|miniaturadaimagem|Solução numérica do sistema de equações diferenciais sem atraso obtido via Mathematica.]] | |||
Além disto, pode-se verificar que <math display="inline">i^{*}\approx0.45</math> e <math display="inline">c^{*}=\beta s^{*}i^{*}\tau_{i}\approx0.45</math>, concordando com nossos cálculos analíticos. Isto implica que no equilíbrio, a população total infecciosa em um instante <math display="inline">t</math> é sempre dada inteiramente pelos que foram infectados durante um período anterior <math display="inline">t-\tau_{i}</math>, ou seja, a área dada pelo retângulo de largura <math display="inline">\tau_{i}</math> e altura <math display="inline">\beta s^{*}i^{*}</math>, uma vez que no equilíbrio as frações <math display="inline">i\left(t\right)</math> e <math display="inline">s\left(t\right)</math> são constantes. Estes resultados concordam com a suposição de que <math display="inline">c_{1}=0</math>. | |||
Porém tentando o mesmo procedimento para a equação com atraso, obtém-se: | |||
<math display="block">\begin{align} | |||
\frac{di\left(t\right)}{dt}= & \beta s\left(t\right)i\left(t\right)-\beta s\left(t-\tau_{i}\right)i\left(t-\tau_{i}\right)\\ | |||
\int_{i\left(t^{*}-\tau_{i}\right)}^{i\left(t^{*}\right)}di= & \int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t-\tau_{i}\right)i\left(t-\tau_{i}\right)dt\\ | |||
i\left(t^{*}\right)= & \int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau_{i}\right)-\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t-\tau_{i}\right)i\left(t-\tau_{i}\right)dt\right]{eq:cat}\end{align}</math> | |||
Utilizando a consideração <math display="inline">i\left(t^{*}\right)=i\left(t^{*}-\tau_{i}\right)</math>, é possível obter apenas <math display="inline">i\left(t^{*}\right)=i\left(t^{*}\right)</math>. Para recuperar a equação original seria necessário que, de modo análogo a equação sem atraso, a seguinte igualdade fosse válida: | |||
<math display="block">i\left(t^{*}\right)=\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt</math> | |||
Isto é, de modo análogo ao caso anterior, que no equilíbrio a fração de infecciosos em um tempo <math display="inline">t</math> seja dado inteiramente pelos que foram contagiados em um tempo <math display="inline">t-\tau_{i}</math>. Porém neste caso qualquer par de pontos <math display="inline">\left(i^{*},s^{*}\right)</math> poderia consistir em um ponto de equilíbrio para um conjunto de parâmetros <math display="inline">\left\{ \beta,\tau_{i},\tau_{r}\right\}</math> qualquer. A dependência se torna das condições iniciais. Utilizando por exemplo condições iniciais constantes como frequentemente é utilizado na literatura de equações com atraso, a própria condição inicial se torna um ponto de equilíbrio <math display="inline">i_{0}=i^{*}</math>. Pode-se pensar que desta fração <math display="inline">i^{*}</math> de infecciosos , a cada instante <math display="inline">t</math>, uma quantidade de <math display="inline">c=\beta i_{0}s_{0}</math> de infecciosos são curados, porém outra quantidade igual <math display="inline">c</math> de suscetíveis são infectados, mantendo a taxa de variação zerada e a quantidade total de infecciosos constante. Assim sendo, pensando em situações reais, para um instante <math display="inline">t</math>, há quantidade <math display="inline">i_{c}=i_{0}-c</math> da fração que permanece infecciosa mesmo após <math>\tau_i</math>, que soma-se aos novos infectados, mantendo a fração constante. Isto é, para a equação: | |||
<math display="block">i\left(t\right)=c_{1}+\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt</math> | |||
Então <math display="inline">c_{1}\neq0</math>. Para retirar esta constante, pode-se pensar que é como se no equilíbrio precisasse de <math display="block">n=\frac{i_{0}}{c}=\frac{i_{0}}{\beta i_{0}s_{0}}=\frac{1}{\beta s_{0}}</math> tempo para que uma pessoa infecciosa se curasse, ao invés de <math display="inline">\tau_{i}</math>. Pois após <math display="inline">n</math> tempo toda a população <math display="inline">i_{0}</math> terá sido substituída por uma nova população infecciosa isto é <math display="inline">i_{0}-nc=0</math>, uma vez que a cada instante <math display="inline">t=n</math> tem-se que uma fração <math display="inline">c</math> da população suscetível sendo infectada, e outra fração <math>c</math> da população infecciosa que se recuperou pois foi infectada em um instante anterior <math display="inline">t-\tau_{i}</math>. . Reescrevendo a integral com este novo limite | |||
<math display="block">i\left(t\right)=\int_{t^{*}-n}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt=\beta s^{*}i^{*}n=\frac{\beta s^{*}i^{*}}{\beta s_{0}}=i^{*}</math> | |||
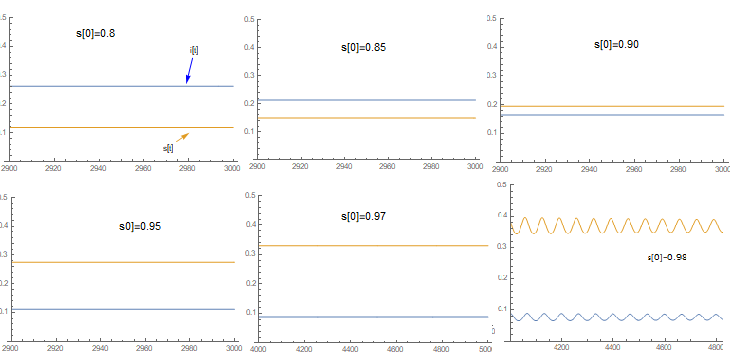
Uma vez que <math display="inline">s_{0}=s^{*}</math> para estas condições iniciais. Além disto, a expressão para <math>n</math> é análoga a equação encontrada para o ponto de equilíbrio do sistema sem atraso, isto é <math display="inline">\tau_{i}=1/ \beta s^{*}</math>. Toda discussão foi feita para condições iniciais constantes, quando se utiliza o método proposto, a análise torna-se mais complicada, mas ainda é notável que o ponto de equilíbrio depende das condições iniciais.Utilizando o conjunto de parâmetros <math display="inline">\beta=0.4</math>, <math display="inline">\tau_{i}=5</math> e <math display="inline">\tau_{r}=50</math>, para diferentes valores iniciais é possível obter: | |||
[[Ficheiro:Com_atraso.png|centro|miniaturadaimagem|730x357px|Solução em equilíbrio do sistema de equações diferenciais com atraso para diferentes valores iniciais de infecciosos.]] | |||
Pode-se notar que aproximadamente: | |||
<div class="center", align="center"> | |||
{| class="wikitable" | |||
! align="center" |<math display="inline">i_{0}=</math> | |||
! align="center" |<math display="inline">\tau_{i}c\approx</math> | |||
! align="center" |<math display="inline">i^{*}\approx</math> | |||
|- | |||
| align="center" |<math display="inline">0.20</math> | |||
| align="center" |<math display="inline">0.06</math> | |||
| align="center" |<math display="inline">0.26</math> | |||
|- | |||
| align="center" |<math display="inline">0.15</math> | |||
| align="center" |<math display="inline">0.06</math> | |||
| align="center" |<math display="inline">0.21</math> | |||
|- | |||
| align="center" |<math display="inline">0.10</math> | |||
| align="center" |<math display="inline">0.06</math> | |||
| align="center" |<math display="inline">0.16</math> | |||
|- | |||
| align="center" |<math display="inline">0.05</math> | |||
| align="center" |<math display="inline">0.06</math> | |||
| align="center" |<math display="inline">0.11</math> | |||
|} | |||
</div> | |||
Lembrando da integral proposta para a condição de equilíbrio condição de equilíbrio: | |||
<math display="block">\begin{align} | |||
i\left(t\right) & = c_1 +\int_{t^{*}-\tau_{i}}^{t^{*}}c\left(t\right)dt{eq:veinte}\end{align}</math> | |||
Novamente <math display="inline">c_{1}\neq0</math>, mais especificamente <math>i_0=c_1</math>. Este resultado faz sentido, pois de acordo com o procedimento proposto, não há momento em que os infecciosos iniciais <math display="inline">i_{0}</math> se recuperam. Durante o tempo <math display="inline">0\leq t<\tau_{i}</math> uma fração da população se infecta, e então esta mesma fração começa a se recuperar após <math display="inline">t>\tau_{i}</math>, mas os infecciosos iniciais, nunca se recuperam, funcionando como fontes permanentes de infecção. Outra forma de comparar, é que olhando o conjunto de equações diferenciais originais o termo responsável pela recuperação dos infecciosos no instante <math display="inline">t</math> depende da quantidade total de infecciosos no próprio instante <math display="inline">t</math>. No conjunto de equações com atraso, é a fração da população da população que foi contagiada em um instante anterior. Ou seja, uma fração da população que se infectou em um instante <math display="inline">t</math>, é a mesma que se recuperara em um instante posterior <math display="inline">t+\tau_{i}</math>, porém a quantidade inicial de infecciosos não se contagiou em nenhum momento desta ’linha do tempo', então também não se recuperam em nenhum momento. | |||
Porém ainda que <math display="inline">c_{1}\neq0</math>, quanto mais próximo a população inicial de infecciosos for de <math display="inline">0</math>, melhor será aproximação, Por isso a análise em torno do ponto de equilíbrio, e o próprio ponto de equilíbrio se torna uma aproximação válida apenas quando é adotado valores próximos de <math display="inline">0</math> para <math display="inline">i_{0}</math>. | |||
=== Análise do ponto de equilíbrio === | |||
==== Obtendo a equação transcendental ==== | |||
Aplicando então uma perturbação nos pontos de equilíbrios, isto é: <math display="inline">s\left(t\right)=s^{*}+x\left(t\right)</math> e <math display="inline">i</math><math display="inline">\left(t\right)=i^{*}+y\left(t\right)</math> pode-se obter uma aproximação linear em torno do ponto de equilíbrio (uma observação é que o teste utilizando os limites leva a uma indeterminação, uma vez que não há termo linear). Então analisando o termo que chamamos de contágios: | |||
<math display="block">\begin{align} | |||
c\left(t\right) & =\beta s\left(t\right)i\left(t\right)\\ | |||
\frac{c\left(t\right)}{\beta} & =\left(s^{*}+x\left(t\right)\right)\left(i^{*}+y\left(t\right)\right)\\ | |||
& =s^{*}i^{*}+i^{*}x\left(t\right)+s^{*}y\left(t\right)+x\left(t\right)y\left(t\right)\end{align}</math> | |||
Ignorando os termos não lineares e denotando <math display="inline">f\left(t\right)=f</math> e <math display="inline">f\left(t-\tau\right)=f_{\tau}</math>: | |||
<math display="block">\begin{align} | |||
\frac{c}{\beta} & =s^{*}i^{*}+i^{*}x+s^{*}y\end{align}</math> | |||
Tem-se então: | |||
<math display="block">\begin{align} | |||
\frac{\dot{x}}{\beta}= & -\left(s^{*}i^{*}+i^{*}x+s^{*}y\right)+\left(s^{*}i^{*}+i^{*}x_{\tau_{0}}+s^{*}y_{\tau_{0}}\right)\\ | |||
& =-\left(i^{*}x+s^{*}y\right)+\left(i^{*}x_{\tau_{0}}+s^{*}y_{\tau_{0}}\right)\end{align}</math> | |||
E: | |||
<math display="block">\begin{align} | |||
\frac{\dot{y}}{\beta}= & -\left(s^{*}i^{*}+i^{*}x_{\tau_{i}}+s^{*}y_{\tau_{i}}\right)+\left(s^{*}i^{*}+i^{*}x+s^{*}y\right)\\ | |||
& =\left(i^{*}x+s^{*}y\right)-\left(i^{*}x_{\tau_{i}}+s^{*}y_{\tau_{i}}\right)\end{align}</math> | |||
O sistema linearizado em torno do ponto de equilíbrio é então: | |||
<math display="block">\begin{align} | |||
\frac{\dot{x}}{\beta} & =-\left(i^{*}x+s^{*}y\right)+\left(i^{*}x_{\tau_{0}}+s^{*}y_{\tau_{0}}\right)\\ | |||
\frac{\dot{y}}{\beta} & =+\left(i^{*}x+s^{*}y\right)-\left(i^{*}x_{\tau_{i}}+s^{*}y_{\tau_{i}}\right)\end{align}</math>Reescrevendo matricialmente:<math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\beta\left(\begin{array}{cc} | |||
-i^{*} & -s^{*}\\ | |||
i^{*} & s^{*} | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)+\beta\left(\begin{array}{cc} | |||
i^{*} & s^{*}\\ | |||
0 & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x_{\tau_{0}}\\ | |||
y_{\tau_{0}} | |||
\end{array}\right)+\beta\left(\begin{array}{cc} | |||
0 & 0\\ | |||
-i^{*} & -s^{*} | |||
\end{array}\right)\left(\begin{array}{c} | |||
x_{\tau_{i}}\\ | |||
y_{\tau_{i}} | |||
\end{array}\right)</math>Ou ainda:<math display="block">\dot{\boldsymbol{x}}\left(t\right)=A_{0}\boldsymbol{x}+A_{1}\boldsymbol{x}\left(t-\tau_{0}\right)+A_{2}\boldsymbol{x}\left(t-\tau_{i}\right)</math> | |||
A equação característica para um sistema do tipo: | |||
<math display="block">\dot{\boldsymbol{x}}\left(t\right)=A_{0}\boldsymbol{x}\left(t\right)+\sum_{i=1}^{k}A_{i}\boldsymbol{x}\left(t-T_{i}\right)</math> É dado por: | |||
<math display="block">\det\left[\Delta\left(\lambda\right)\right]=\det\left[\lambda\mathbb{I}-A_{0}-\sum_{i=1}^{k}A_{i}e^{-\lambda T_{i}}\right]</math> | |||
A função <math display="inline">\Delta\left(\lambda\right)</math> é chamada de quase-polinômio característico. Como de costume, se para para todo <math display="inline">\lambda\in\mathbb{C}</math>, for <math display="inline">Re\left(\lambda\right)<0</math> o sistema é assintoticamente estável. | |||
Detalhes: | |||
* Se não houver atraso, a equação é reduzida a <math display="inline">\det\left[\lambda\mathbb{I}-A_{0}\right]</math>. Como para achar as raízes deve-se fazer <math display="inline">\det\left[\Delta\left(\lambda\right)\right]=0</math>, obtém-se o resultado tradicional. | |||
* Se houver apenas uma equação, e não um sistema, então os termos <math display="inline">A_{j}</math> serão constantes e não uma matrizes. Substituindo <math display="inline">x\left(t\right)=ce^{\lambda t}</math>: | |||
<math display="block">\begin{align} | |||
\lambda ce^{\lambda t} & =A_{0}ce^{\lambda t}+\sum_{i=1}^{k}A_{i}ce^{\lambda t}e^{-\lambda T_{i}}\\ | |||
\lambda & =A_{0}+\sum_{i=1}^{k}A_{i}e^{-\lambda T_{i}}\end{align}</math> | |||
Então: | |||
<math display="block">\lambda-A_{0}-\sum_{i=1}^{k}A_{i}e^{-\lambda T_{i}}=0</math> | |||
Obtém-se o quase-polinômio característico proposto pro sistema conforme. Dessa forma, a equação transcendental característica para o sistema que estamos interessados é: | |||
<math display="block">\begin{align} | |||
\det\left[\Delta\left(\lambda\right)\right]= & \det\left[\lambda\mathbb{I}-A_{0}-A_{1}e^{-\lambda\tau_{0}}-A_{2}e^{-\lambda\tau_{i}}\right]\\ | |||
= & \det\left[\left(\begin{array}{cc} | |||
\lambda & 0\\ | |||
0 & \lambda | |||
\end{array}\right)-\beta\left(\begin{array}{cc} | |||
-i^{*} & -s^{*}\\ | |||
i^{*} & s^{*} | |||
\end{array}\right)-\beta\left(\begin{array}{cc} | |||
i^{*} & s^{*}\\ | |||
0 & 0 | |||
\end{array}\right)e^{-\lambda\tau_{0}}+\beta\left(\begin{array}{cc} | |||
0 & 0\\ | |||
i^{*} & s^{*} | |||
\end{array}\right)e^{-\lambda\tau_{i}}\right]\\ | |||
= & \det\left[\left(\begin{array}{cc} | |||
\lambda+\beta i^{*}\left(1-e^{-\lambda\tau_{0}}\right) & \beta s^{*}\left(1-e^{-\lambda\tau_{0}}\right)\\ | |||
\beta i^{*}\left(e^{-\lambda\tau_{i}}-1\right) & \lambda+\beta\left(e^{-\lambda\tau_{i}}-1\right)s^{*} | |||
\end{array}\right)\right]\\ | |||
= & \left[\lambda+\beta i^{*}\left(1-e^{-\lambda\tau_{0}}\right)\right]\left[\lambda+\beta\left(e^{-\lambda\tau_{i}}-1\right)s^{*}\right]-i^{*}\beta\left(e^{-\lambda\tau_{i}}-1\right)s^{*}\beta\left(1-e^{-\lambda\tau_{0}}\right)\\ | |||
= & \lambda^{2}+\lambda\beta\left[s^{*}\left(e^{-\lambda\tau_{i}}-1\right)-i^{*}\left(e^{-\lambda\tau_{0}}-1\right)\right]+\beta^{2}s^{*}i^{*}\left(e^{-\lambda\tau_{i}}-1\right)\left(1-e^{-\lambda\tau_{0}}\right)-\beta^{2}s^{*}i^{*}\left(e^{-\lambda\tau_{i}}-1\right)\left(1-e^{-\lambda\tau_{0}}\right)\\ | |||
= & \lambda^{2}+\lambda\beta\left[s^{*}\left(e^{-\lambda\tau_{i}}-1\right)-i^{*}\left(e^{-\lambda\tau_{0}}-1\right)\right]\end{align}</math> | |||
Para encontrar as raízes | |||
<math display="block">\begin{align} | |||
\lambda^{2}+\lambda\beta\left[s^{*}\left(e^{-\lambda\tau_{i}}-1\right)-i^{*}\left(e^{-\lambda\tau_{0}}-1\right)\right] & =0\end{align}</math> | |||
Esta equação é chamada de equação característica transcendental. Uma raiz é <math display="inline">\lambda=0</math>, e a outra pode ser obtida a partir de: | |||
<math display="block">\begin{align} | |||
\lambda+\beta\left[s^{*}\left(e^{-\lambda\tau_{i}}-1\right)-i^{*}\left(e^{-\lambda\tau_{0}}-1\right)\right] & =0\end{align}</math> | |||
Como uma raiz é <math display="inline">\lambda_{1}=0</math>, se <math display="inline">\lambda_{2}>0</math> há um equilíbrio instável próximo ao ponto de equilíbrio. | |||
* Observações: | |||
** [https://en.wikipedia.org/wiki/Transcendental_equation Equação transcendental]: equação que contém uma função transcendental da variável que deve ser resolvida. | |||
** [https://en.wikipedia.org/wiki/Transcendental_function Função transcendental]: função que não satisfaz uma equação polinomial, em contraste com uma função algébrica, isto é, transcende a álgebra”. Um exemplo é a função exponencial. | |||
** [https://en.wikipedia.org/wiki/Algebraic_function Função algébrica]: função que pode ser definida como a raiz de uma equação polinomial. | |||
Soluções aproximadas são obtidas por métodos gráficos conforme feito anteriormente para soluções reais em [[Análise de estabilidade de equações diferenciais lineares atrasadas |Equações diferenciais com atrasos]], ou até simplesmente observando o gráfico. Mas neste caso será utilizado algoritmos. | |||
==== Obtendo as raízes da equação transcendental ==== | |||
===== Método de Newton ===== | |||
Também conhecido como método de Newton-Raphson, aproxima a função com uma linha. Esta linha atravessa o ponto <math display="inline">\left(x_{i},f\left(x_{i}\right)\right)</math> e tem inclinação igual a derivada da própria função. Matematicamente isto é: | |||
<math display="block">\begin{align} | |||
f'\left(x_{i}\right)= & \frac{y_{i+1}-f\left(x_{i}\right)}{x_{i+1}-x_{i}}\\ | |||
x_{i+1}= & x_{i}+\frac{\left(y_{i+1}-f\left(x_{i}\right)\right)}{f'\left(x_{i}\right)}\end{align}</math> | |||
Então encontra-se o <math display="inline">x</math> que atravessa o eixo e o utiliza como uma nova tentativa. Ou seja o segundo ponto sobre a reta é <math display="inline">\left(x_{i+1},0\right)</math>, então: | |||
<math display="block">\begin{align} | |||
x_{i+1}= & x_{i}-\frac{f\left(x_{i}\right)}{f'\left(x_{i}\right)}\end{align}</math> | |||
Para estender o método para o plano complexo, basta substituir variável real <math display="inline">x</math> por uma variável complexa <math display="inline">z=x+yi</math>. A partir disto, o loop é repetido. | |||
===== Aplicando o método ===== | |||
Então sendo: | |||
<math display="block">\begin{align} | |||
f\left(\lambda\right) & =\lambda+\beta\left[s^{*}\left(e^{-\lambda\tau_{i}}-1\right)-i^{*}\left(e^{-\lambda\tau_{0}}-1\right)\right]\\ | |||
f'\left(\lambda\right) & =1+\beta\left[\tau_{0}i^{*}e^{-\lambda\tau_{0}}-s^{*}\tau_{i}e^{-\lambda\tau_{i}}\right]\end{align}</math> | |||
Foi utilizado um algoritmo em Python para buscar as raízes complexas. O gráfico original é <math display="inline">R_{0}\times\frac{\tau_{r}}{\tau_{i}}</math>. Onde <math display="inline">R_{0}=\beta\tau_{i}</math> é chamado de taxa de reprodução básica. Para facilitar foi escolhido denotar <math display="inline">R_{1}=\frac{\tau_{r}}{\tau_{i}}</math>. Com poucas manipulações é possível mostrar que: | |||
<math display="block">\begin{align} | |||
\tau_{i}= & \frac{R_{0}}{\beta}\\ | |||
\tau_{r}= & \frac{R_{1}R_{0}}{\beta}\end{align}</math> | |||
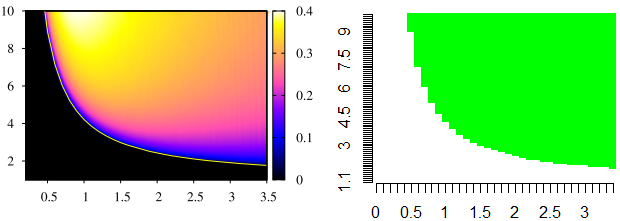
Assim para um <math display="inline">\beta</math> constante pode-se variar apenas <math display="inline">R_{0}</math> e <math display="inline">R_{1}</math>. Deste modo o algoritmo proposto busca a existência de raízes com parte real positiva, isto é, o conjunto de equações apresenta comportamento instável na proximidade do ponto de equilíbrio. Esta busca ocorre para cada par de valores <math display="inline">\left(R_{1},R_{0}\right)</math> na malha formada por <math display="inline">R_{0}\times R_{1}</math>, onde <math display="inline">1<R_{0}<10</math> e <math display="inline">0\leq R_{1}<3.5</math>, com intervalos de <math display="inline">\Delta=0.1</math>. Especificamente em cada par de valores é executado o algoritmo de Newton-Raphson com o chute inicial partindo de cada ponto possível do plano complexo dentro da região delimitada por <math display="inline">-1\leq\mathbb{R}\left(\lambda\right),\mathbb{I}\left(\lambda\right)<1</math> , com espaçamento entre os pontos de <math>\Delta=0.1</math>. Isto ocorre enquanto nenhuma raiz com parte real positiva seja encontrada, além disso, é realizada no máximo <math>N=10^7</math> tentativas de aproximação, e é considerado <math>f\left(x\right)=0</math> se <math>\left|f\left(x\right)\right|<10^{-12}</math>. | |||
[[Ficheiro:raizes.png|centro|miniaturadaimagem|620x221px|A esquerda a imagem original retirada do artigo. A região preta são soluções sem oscilação e a colorida onde há a presença de oscilações. A direita a imagem obtida através do algoritmo proposto onde a região verde indica que foi encontrado autovalores positivos.]] | |||
=== Algoritmos === | |||
O conjunto de equações diferenciais sem atraso pode ser solucionado via [https://www.wolfram.com/mathematica/index.html.pt-br?footer=lang Mathematica]: | |||
tmax = 400; b = 0.4; ti = 5; tr = 5; | |||
sol = NDSolve[{ | |||
s'[t] == -b*s[t]*i[t] + r[t]/tr, | |||
i'[t] == +b*s[t]*i[t] - i[t]/ti, | |||
r'[t] == i[t]/ti - r[t]/tr, | |||
s[0] == 0.5, i[0] == 0.5, r[0] == 0}, | |||
{s, i, r}, {t, 0, 500}]; | |||
Plot[{i[t] /. sol, s[t]} /. sol, {t, 0, 500}, PlotRange -> {0., 1.}] | |||
O sistema de equações diferenciais com atraso pode ser pode ser solucionado via [https://www.python.org/ Python] utilizando o método de Euler conforme proposto : | |||
import matplotlib.pyplot as plt | |||
import numpy as np | |||
#Função para resolver o sistema de equações diferenciais | |||
def sistema(R0,R1): | |||
#Parâmetro R0=b.ti | |||
#Parâmetro R1=tr/ti | |||
#Parâmetros da dinâmica | |||
b =4 | |||
ti=R0/b | |||
tr=R1*R0/b | |||
to=ti+tr | |||
# Listas para guardar a evolução do sistema | |||
s=[] | |||
i=[] | |||
d=0.001 #Passo para o método de Euler | |||
#Primeira parte: | |||
N1=int(ti/d) #Quantidade de passos | |||
i.append(1e-16) #Condição inicial de inectado i0 | |||
s.append(1-i[0]) #Condição inicial de suscetíveis s0=1-i0 | |||
#Resolve o sistema Usando o método de Euler | |||
for k in range(N1): | |||
s.append(s[k]+d*(-b*s[k]*i[k])) | |||
i.append(i[k]+d*(b*s[k]*i[k])) | |||
#Segunda parte | |||
N2=int(to/d) | |||
for k in range(N1,N2): | |||
s.append(s[k]+d*(-b*s[k]*i[k])) | |||
i.append(i[k]+d*(b*s[k]*i[k]-b*s[k-int(ti/d)]*i[k-int(ti/d)])) | |||
#Terceira parte | |||
N3=int(1800/d) | |||
for k in range(N2,N3): | |||
s.append(s[k]+d*(-b*s[k]*i[k]+b*s[k-int(to/d)]*i[k-int(to/d)])) | |||
i.append(i[k]+d*(+b*s[k]*i[k]-b*s[k-int(ti/d)]*i[k-int(ti/d)])) | |||
O sistema também pode ser resolvido via Mathematica: | |||
b = 0.8; ti = 5; to = 20; | |||
ci1 = NDSolve[{ | |||
s1'[t] == -b*s1[t]*i1[t], | |||
i1'[t] == +b*s1[t]*i1[t], | |||
s1[0] == 0.99, i1[0] == 0.01}, | |||
{s1, i1}, {t, 0, ti}]; | |||
ci2 = NDSolve[{ | |||
s2'[t] == -b*s2[t]*i2[t], | |||
i2'[t] == +b*s2[t]*i2[t] - b*s2[t - ti]*i2[t - ti], | |||
s2[t /; t <= ti] == s1[t] /. ci1, | |||
i2[t /; t <= ti] == i1[t] /. ci1}, | |||
{s2, i2}, {t, 0, to}]; | |||
sol = NDSolve[{ | |||
s'[t] == -b*s[t]*i[t] + b*s[t - to]*i[t - to], | |||
i'[t] == +b*s[t]*i[t] - b*s[t - ti]*i[t - ti], | |||
s[t /; t <= to] == s2[t] /. ci2, i[t /; t <= to] == i2[t] /. ci2}, | |||
{s, i}, {t, 0, 300}]; | |||
Plot[{i[t] /. sol, s[t] /. sol}, {t, 0, 300}, PlotRange -> {0., 1.}] | |||
O código abaixo foi escrito em Python e é responsável por buscas raízes complexas com a parte real positiva na equação transcendental discutida anteriormente. | |||
#Código para resolver a equação transcendental | |||
def raizes(): | |||
sol=np.zeros((35,90)) # Matriz para guardar as raízes | |||
err=1e-12 # Erro admitido | |||
sy=0 | |||
for R0 in np.arange(1,10,0.1): #Percorrer os valores RO=b. | |||
print(str(100*(sy+1)/90)+"%") | |||
sx=0 | |||
for R1 in np.arange(0,3.5,0.1): #Percorrer os valores R1=tr/ti | |||
#Parâmetros da dinâmica | |||
b =4 | |||
ti=R0/b | |||
tr=R1*R0/b | |||
to=ti+tr | |||
#Pontos de equilíbrio | |||
io=(b*ti-1)/(b*to) | |||
so=1/(b*ti) | |||
#Matriz das raízes para os parâmetros atuais | |||
r=np.zeros((20, 20)) | |||
#Os chutes iniciais serão pontos dentro da malha [-1,1] em 2D | |||
m=0 | |||
for a in np.arange(-1,1,0.1): | |||
n=0 | |||
for y in np.arange(-1,1,0.1): | |||
i=y*1j | |||
x=a+i # Ponto inicial | |||
N=10000000 # Quantidade máxima de aproximações | |||
#Valor da função para o chute inicial | |||
f=x+b*(so*(np.power(np.e,-x*ti)-1)-io*(np.power(np.e,-x*to)-1)) | |||
for k in range(N): | |||
if (k==N-2): | |||
print("!") #Indicando que chegou no último passo sem achar a raízs | |||
if (abs(f)<err): | |||
break # Se chou a raíz, do loop | |||
try: | |||
f =x+b*(so*(np.power(np.e,-x*ti)-1)-io*(np.power(np.e,-x*to)-1)) | |||
df=1+b*(to*io*np.power(np.e,-x*to)-ti*so*np.power(np.e,-x*ti)) | |||
nx=x-f/df # Próximo chute | |||
x=nx | |||
except: | |||
print(str(R0)+","+str(R1)) | |||
break | |||
if(abs(np.real(x))<err): # A raíz é zero | |||
r[m,n]=0 | |||
elif (np.real(x)>0): # Raíz positiva | |||
r[m,n]=1 | |||
break | |||
else: | |||
r[m,n]=-1 # Raíz negativa | |||
n=n+1 | |||
else: # Quando acabar o loop interno | |||
m=m+1 | |||
continue # Continua | |||
break # Se o loop interno foi encerrado antes da hora, encerra o externo | |||
res=[] | |||
for i in range(20): | |||
res.append(max(r[i])) | |||
sol[sx,sy]=max(res) # Se houve raíz positiva, obtém. | |||
sx=sx+1 | |||
sy=sy+1 | |||
#Registra | |||
f = open("raizes.dat", "w") | |||
for i in sol: | |||
for j in i: | |||
f.write(str(j)+" ") | |||
f.write("\n") | |||
f.close() | |||
raizes() | |||
A partir dos dados gerados com o código anterior, é possível visualizá-los em [https://www.r-project.org/ R] com o seguinte código: | |||
library('tseries') #Bibliotea pra ler matriz | |||
library('plot.matrix') #Biblioteca pra plotar matriz | |||
m <- read.matrix( "Raizes.dat") #Os dados são lidos no formato de matriz | |||
m<-t(m) # São feitas algumas correções devido à ordem que os dados são gravados | |||
m <-m[90:2, 1:35] | |||
rownames(m) <- (99:11)/10 #Ajusta-se os nomes das linhas e colunas | |||
colnames(m) <- (0:34)/10 | |||
#E plota-se | |||
plot(m, col=c('black', 'white', 'green'), breaks=c(-2, -0.25,0.25, 2), xlab='R1', ylab='R0',main='Raizes',border=NA) | |||
=== Principais materiais utilizados === | |||
# [https://arxiv.org/abs/0912.1250 Oscillations in SIRS model with distributed delays] (S. Gonçalves e outros, The European Physical Journal B) | |||
# [http://physics.wm.edu/~evmik/classes/matlab_book/ch_root_finding/ch_root_finding.pdf Root finding algorithms] (Eugeniy E. Mikhailov, Faculdade de William e Mary) | |||
# [https://www.research-collection.ethz.ch/bitstream/handle/20.500.11850/142209/eth-39927-02.pdf Stability and stabilization of time-delay systems] ( Gerhard Manfred Schoen ,Instituto Federal de Tecnologia de Zurique) | |||
{{Ecologia| [[Análise de estabilidade de equações diferenciais lineares atrasadas | Exemplo: equação diferencial com retardo ]] |[[Simulação e modelo de campo médio]]}} | |||
Edição atual tal como às 14h50min de 30 de junho de 2021
Anterior: Exemplo: equação diferencial com retardo | Índice: Ecologia | Próximo: Simulação e modelo de campo médio
O sistema
O exemplo a ser considerado é da biologia matemática, muitas ferramentas matemáticas utilizado na dinâmica de populações encontra-se também na dinâmica de epidemias. O objetivo deste tópico não é se aprofundar na modelagem em si, mas a utilizar como motivação para compreender melhor os sistemas de equações diferenciais com atraso baseado no artigo "Oscillations in SIRS model with distributed delays".
Uma doença do tipo SIRS é caracterizada por um tempo de infecção e um tempo de imunidade . Isto é, um indivíduo que se infecte em um tempo vai deterministicamente se recuperar em um tempo , tornando-se temporariamente imune por um tempo . Então no instante perde a imunidade tornando-se suscetível novamente. Este sistema pode ser representado por um conjunto de equações para a fração de população infecciosa (e infectada) e suscetível :
Onde é a taxa de contágio por indivíduo. A fração da subpopulação em recuperação (imune) é dada por . O primeiro termos em ambas as equações representa o contágio dos suscetíveis pelos infecciosos, daqui em diante muitas vezes será referido como: . Os segundos termos representam a recuperação ou a perda de imunidade após e decorrido desde a infecção, respectivamente. Isto é:
Em outras palavras, uma fração se contagia no instante , no instante ela se recupera, diminuindo os infecciosos. No instante ela perde a imunidade, aumentando a quantidade de suscetíveis. Estas equações exigem condições iniciais, matematicamente usualmente se fornece funções arbitrárias e no intervalo . Porém de um ponto de vista epidemiológico, é razoável prover condições iniciais em e dinâmicas complementares nos intervalos e .
- somente contágio local. Utiliza-se as equações apenas com os primeiros termos, sem atraso.
- Transição do estágio de infeccioso para em recuperação, ou seja, retira-se apenas o segundo termo na equação da dinâmica dos suscetíveis.
E com as condições iniciais:
Ponto de equilíbrio
Para análise dos pontos de equilíbrio uma representação integral é uma forma melhor forma de representar o sistema, pois se fizermos algo análogo ao que foi feito em Equações diferenciais com atrasos, não será possível obter nenhuma informação sobre o ponto de equilíbrio, pois aparentemente qualquer par de valores poderia representar um ponto de equilíbrio. Para a dinâmica dos infecciosos é proposto então:
A interpretação é direta, integra-se sobre sobre todos os indivíduos que se contagiaram entre o tempo e . Estes serão os infecciosos no instante , uma vez que todos infectados anteriormente a este tempo já estarão recuperados. A constante de integração a princípio é arbitrária, mas espera-se que pois não deve haver outras fontes de infecções adicionais. Complementariamente:
Pelo lado esquerdo, pode-se perceber ver que isto se refere a população que não está se recuperando, isto é , ou seja, os infectados e suscetíveis. A integral cobre os contágios que ocorreram durante anterior. Desta forma, esta integral fornece o número de pessoas que estão no período de recuperação, logo é razoável supor que uma vez que também não há outras fontes de pessoas em recuperação. Para um estado de equilíbrio então que a fração de contagiados em um instante qualquer é constante, pode-se escrever . Para :
E para , de maneira análoga:
Uma vez que . Lembrando que , então no estado de equilíbrio , denotando os pontos de equilíbrio apenas como e , obtém-se do primeiro resultado:
E do segundo:
Assim o ponto de equilíbrio é: .
Validade da aproximação e sistema de equações sem atraso
Uma atenção especial deve ser dada a consideração de que quando foi proposto a equação integral para . A formulação matemática do modelo sem atraso é usualmente escrito como:
Integrando a equação da dinâmica de do sistema sem atraso, de a , obtém-se:
Considerando no equilíbrio que :
Sendo que no equilíbrio os valores são constantes e :
De onde é possível obter também o mesmo ponto de equilíbrio obtido anteriormente:
Outra formar de comparar as equações, é que para obter versão integral apresentada para a partir de::
É é necessário que o termo entre colchete seja zerado. Isto é, considerando que no equilíbrio e sejam constantes:
Desta forma a condição imposta anteriormente é recuperada. Agora percebe-se que o ponto de equilíbrio é independente das condições iniciais, depende apenas dos parâmetros escolhidos e . Por exemplo, resolvendo numericamente o sistema de equações diferenciais proposto, com os parâmetros , e , e condições iniciais , o sistema atinge o equilíbrio precisamente nos pontos calculados.
Além disto, pode-se verificar que e , concordando com nossos cálculos analíticos. Isto implica que no equilíbrio, a população total infecciosa em um instante é sempre dada inteiramente pelos que foram infectados durante um período anterior , ou seja, a área dada pelo retângulo de largura e altura , uma vez que no equilíbrio as frações e são constantes. Estes resultados concordam com a suposição de que .
Porém tentando o mesmo procedimento para a equação com atraso, obtém-se:
Utilizando a consideração , é possível obter apenas . Para recuperar a equação original seria necessário que, de modo análogo a equação sem atraso, a seguinte igualdade fosse válida:
Isto é, de modo análogo ao caso anterior, que no equilíbrio a fração de infecciosos em um tempo seja dado inteiramente pelos que foram contagiados em um tempo . Porém neste caso qualquer par de pontos poderia consistir em um ponto de equilíbrio para um conjunto de parâmetros qualquer. A dependência se torna das condições iniciais. Utilizando por exemplo condições iniciais constantes como frequentemente é utilizado na literatura de equações com atraso, a própria condição inicial se torna um ponto de equilíbrio . Pode-se pensar que desta fração de infecciosos , a cada instante , uma quantidade de de infecciosos são curados, porém outra quantidade igual de suscetíveis são infectados, mantendo a taxa de variação zerada e a quantidade total de infecciosos constante. Assim sendo, pensando em situações reais, para um instante , há quantidade da fração que permanece infecciosa mesmo após , que soma-se aos novos infectados, mantendo a fração constante. Isto é, para a equação:
Então . Para retirar esta constante, pode-se pensar que é como se no equilíbrio precisasse de
Uma vez que para estas condições iniciais. Além disto, a expressão para é análoga a equação encontrada para o ponto de equilíbrio do sistema sem atraso, isto é . Toda discussão foi feita para condições iniciais constantes, quando se utiliza o método proposto, a análise torna-se mais complicada, mas ainda é notável que o ponto de equilíbrio depende das condições iniciais.Utilizando o conjunto de parâmetros , e , para diferentes valores iniciais é possível obter:
Pode-se notar que aproximadamente:
Lembrando da integral proposta para a condição de equilíbrio condição de equilíbrio:
Novamente , mais especificamente . Este resultado faz sentido, pois de acordo com o procedimento proposto, não há momento em que os infecciosos iniciais se recuperam. Durante o tempo uma fração da população se infecta, e então esta mesma fração começa a se recuperar após , mas os infecciosos iniciais, nunca se recuperam, funcionando como fontes permanentes de infecção. Outra forma de comparar, é que olhando o conjunto de equações diferenciais originais o termo responsável pela recuperação dos infecciosos no instante depende da quantidade total de infecciosos no próprio instante . No conjunto de equações com atraso, é a fração da população da população que foi contagiada em um instante anterior. Ou seja, uma fração da população que se infectou em um instante , é a mesma que se recuperara em um instante posterior , porém a quantidade inicial de infecciosos não se contagiou em nenhum momento desta ’linha do tempo', então também não se recuperam em nenhum momento.
Porém ainda que , quanto mais próximo a população inicial de infecciosos for de , melhor será aproximação, Por isso a análise em torno do ponto de equilíbrio, e o próprio ponto de equilíbrio se torna uma aproximação válida apenas quando é adotado valores próximos de para .
Análise do ponto de equilíbrio
Obtendo a equação transcendental
Aplicando então uma perturbação nos pontos de equilíbrios, isto é: e pode-se obter uma aproximação linear em torno do ponto de equilíbrio (uma observação é que o teste utilizando os limites leva a uma indeterminação, uma vez que não há termo linear). Então analisando o termo que chamamos de contágios:
Ignorando os termos não lineares e denotando e :
Tem-se então:
E:
O sistema linearizado em torno do ponto de equilíbrio é então:
A equação característica para um sistema do tipo:
A função é chamada de quase-polinômio característico. Como de costume, se para para todo , for o sistema é assintoticamente estável.
Detalhes:
- Se não houver atraso, a equação é reduzida a . Como para achar as raízes deve-se fazer , obtém-se o resultado tradicional.
- Se houver apenas uma equação, e não um sistema, então os termos serão constantes e não uma matrizes. Substituindo :
Então:
Obtém-se o quase-polinômio característico proposto pro sistema conforme. Dessa forma, a equação transcendental característica para o sistema que estamos interessados é:
Para encontrar as raízes
Esta equação é chamada de equação característica transcendental. Uma raiz é , e a outra pode ser obtida a partir de:
Como uma raiz é , se há um equilíbrio instável próximo ao ponto de equilíbrio.
- Observações:
- Equação transcendental: equação que contém uma função transcendental da variável que deve ser resolvida.
- Função transcendental: função que não satisfaz uma equação polinomial, em contraste com uma função algébrica, isto é, transcende a álgebra”. Um exemplo é a função exponencial.
- Função algébrica: função que pode ser definida como a raiz de uma equação polinomial.
Soluções aproximadas são obtidas por métodos gráficos conforme feito anteriormente para soluções reais em Equações diferenciais com atrasos, ou até simplesmente observando o gráfico. Mas neste caso será utilizado algoritmos.
Obtendo as raízes da equação transcendental
Método de Newton
Também conhecido como método de Newton-Raphson, aproxima a função com uma linha. Esta linha atravessa o ponto e tem inclinação igual a derivada da própria função. Matematicamente isto é:
Então encontra-se o que atravessa o eixo e o utiliza como uma nova tentativa. Ou seja o segundo ponto sobre a reta é , então:
Para estender o método para o plano complexo, basta substituir variável real por uma variável complexa . A partir disto, o loop é repetido.
Aplicando o método
Então sendo:
Foi utilizado um algoritmo em Python para buscar as raízes complexas. O gráfico original é . Onde é chamado de taxa de reprodução básica. Para facilitar foi escolhido denotar . Com poucas manipulações é possível mostrar que:
Assim para um constante pode-se variar apenas e . Deste modo o algoritmo proposto busca a existência de raízes com parte real positiva, isto é, o conjunto de equações apresenta comportamento instável na proximidade do ponto de equilíbrio. Esta busca ocorre para cada par de valores na malha formada por , onde e , com intervalos de . Especificamente em cada par de valores é executado o algoritmo de Newton-Raphson com o chute inicial partindo de cada ponto possível do plano complexo dentro da região delimitada por , com espaçamento entre os pontos de . Isto ocorre enquanto nenhuma raiz com parte real positiva seja encontrada, além disso, é realizada no máximo tentativas de aproximação, e é considerado se .
Algoritmos
O conjunto de equações diferenciais sem atraso pode ser solucionado via Mathematica:
tmax = 400; b = 0.4; ti = 5; tr = 5;
sol = NDSolve[{
s'[t] == -b*s[t]*i[t] + r[t]/tr,
i'[t] == +b*s[t]*i[t] - i[t]/ti,
r'[t] == i[t]/ti - r[t]/tr,
s[0] == 0.5, i[0] == 0.5, r[0] == 0},
{s, i, r}, {t, 0, 500}];
Plot[{i[t] /. sol, s[t]} /. sol, {t, 0, 500}, PlotRange -> {0., 1.}]
O sistema de equações diferenciais com atraso pode ser pode ser solucionado via Python utilizando o método de Euler conforme proposto :
import matplotlib.pyplot as plt
import numpy as np
#Função para resolver o sistema de equações diferenciais
def sistema(R0,R1):
#Parâmetro R0=b.ti
#Parâmetro R1=tr/ti
#Parâmetros da dinâmica
b =4
ti=R0/b
tr=R1*R0/b
to=ti+tr
# Listas para guardar a evolução do sistema
s=[]
i=[]
d=0.001 #Passo para o método de Euler
#Primeira parte:
N1=int(ti/d) #Quantidade de passos
i.append(1e-16) #Condição inicial de inectado i0
s.append(1-i[0]) #Condição inicial de suscetíveis s0=1-i0
#Resolve o sistema Usando o método de Euler
for k in range(N1):
s.append(s[k]+d*(-b*s[k]*i[k]))
i.append(i[k]+d*(b*s[k]*i[k]))
#Segunda parte
N2=int(to/d)
for k in range(N1,N2):
s.append(s[k]+d*(-b*s[k]*i[k]))
i.append(i[k]+d*(b*s[k]*i[k]-b*s[k-int(ti/d)]*i[k-int(ti/d)]))
#Terceira parte
N3=int(1800/d)
for k in range(N2,N3):
s.append(s[k]+d*(-b*s[k]*i[k]+b*s[k-int(to/d)]*i[k-int(to/d)]))
i.append(i[k]+d*(+b*s[k]*i[k]-b*s[k-int(ti/d)]*i[k-int(ti/d)]))
O sistema também pode ser resolvido via Mathematica:
b = 0.8; ti = 5; to = 20;
ci1 = NDSolve[{
s1'[t] == -b*s1[t]*i1[t],
i1'[t] == +b*s1[t]*i1[t],
s1[0] == 0.99, i1[0] == 0.01},
{s1, i1}, {t, 0, ti}];
ci2 = NDSolve[{
s2'[t] == -b*s2[t]*i2[t],
i2'[t] == +b*s2[t]*i2[t] - b*s2[t - ti]*i2[t - ti],
s2[t /; t <= ti] == s1[t] /. ci1,
i2[t /; t <= ti] == i1[t] /. ci1},
{s2, i2}, {t, 0, to}];
sol = NDSolve[{
s'[t] == -b*s[t]*i[t] + b*s[t - to]*i[t - to],
i'[t] == +b*s[t]*i[t] - b*s[t - ti]*i[t - ti],
s[t /; t <= to] == s2[t] /. ci2, i[t /; t <= to] == i2[t] /. ci2},
{s, i}, {t, 0, 300}];
Plot[{i[t] /. sol, s[t] /. sol}, {t, 0, 300}, PlotRange -> {0., 1.}]
O código abaixo foi escrito em Python e é responsável por buscas raízes complexas com a parte real positiva na equação transcendental discutida anteriormente.
#Código para resolver a equação transcendental
def raizes():
sol=np.zeros((35,90)) # Matriz para guardar as raízes
err=1e-12 # Erro admitido
sy=0
for R0 in np.arange(1,10,0.1): #Percorrer os valores RO=b.
print(str(100*(sy+1)/90)+"%")
sx=0
for R1 in np.arange(0,3.5,0.1): #Percorrer os valores R1=tr/ti
#Parâmetros da dinâmica
b =4
ti=R0/b
tr=R1*R0/b
to=ti+tr
#Pontos de equilíbrio
io=(b*ti-1)/(b*to)
so=1/(b*ti)
#Matriz das raízes para os parâmetros atuais
r=np.zeros((20, 20))
#Os chutes iniciais serão pontos dentro da malha [-1,1] em 2D
m=0
for a in np.arange(-1,1,0.1):
n=0
for y in np.arange(-1,1,0.1):
i=y*1j
x=a+i # Ponto inicial
N=10000000 # Quantidade máxima de aproximações
#Valor da função para o chute inicial
f=x+b*(so*(np.power(np.e,-x*ti)-1)-io*(np.power(np.e,-x*to)-1))
for k in range(N):
if (k==N-2):
print("!") #Indicando que chegou no último passo sem achar a raízs
if (abs(f)<err):
break # Se chou a raíz, do loop
try:
f =x+b*(so*(np.power(np.e,-x*ti)-1)-io*(np.power(np.e,-x*to)-1))
df=1+b*(to*io*np.power(np.e,-x*to)-ti*so*np.power(np.e,-x*ti))
nx=x-f/df # Próximo chute
x=nx
except:
print(str(R0)+","+str(R1))
break
if(abs(np.real(x))<err): # A raíz é zero
r[m,n]=0
elif (np.real(x)>0): # Raíz positiva
r[m,n]=1
break
else:
r[m,n]=-1 # Raíz negativa
n=n+1
else: # Quando acabar o loop interno
m=m+1
continue # Continua
break # Se o loop interno foi encerrado antes da hora, encerra o externo
res=[]
for i in range(20):
res.append(max(r[i]))
sol[sx,sy]=max(res) # Se houve raíz positiva, obtém.
sx=sx+1
sy=sy+1
#Registra
f = open("raizes.dat", "w")
for i in sol:
for j in i:
f.write(str(j)+" ")
f.write("\n")
f.close()
raizes()
A partir dos dados gerados com o código anterior, é possível visualizá-los em R com o seguinte código:
library('tseries') #Bibliotea pra ler matriz
library('plot.matrix') #Biblioteca pra plotar matriz
m <- read.matrix( "Raizes.dat") #Os dados são lidos no formato de matriz
m<-t(m) # São feitas algumas correções devido à ordem que os dados são gravados
m <-m[90:2, 1:35]
rownames(m) <- (99:11)/10 #Ajusta-se os nomes das linhas e colunas
colnames(m) <- (0:34)/10
#E plota-se
plot(m, col=c('black', 'white', 'green'), breaks=c(-2, -0.25,0.25, 2), xlab='R1', ylab='R0',main='Raizes',border=NA)
Principais materiais utilizados
- Oscillations in SIRS model with distributed delays (S. Gonçalves e outros, The European Physical Journal B)
- Root finding algorithms (Eugeniy E. Mikhailov, Faculdade de William e Mary)
- Stability and stabilization of time-delay systems ( Gerhard Manfred Schoen ,Instituto Federal de Tecnologia de Zurique)
Anterior: Exemplo: equação diferencial com retardo | Índice: Ecologia | Próximo: Simulação e modelo de campo médio

















![{\textstyle \left[-\tau _{0},0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78093fef9dbf06a6b990659bd088590201247bd7)





























![{\displaystyle {\begin{aligned}{\frac {di\left(t\right)}{dt}}&=\beta s\left(t\right)i\left(t\right)-{\frac {i\left(t\right)}{\tau _{i}}}\\\int _{i\left(t^{*}-\tau _{i}\right)}^{i\left(t^{*}\right)}di&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\\i\left(t^{*}\right)&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\right]{eq:tri}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a453641c87483dc6419ad8f45edce081a2d2c66)






![{\displaystyle i\left(t^{*}\right)=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c115219a9620bbe48ab9463e822f1d8324cfab7)










![{\displaystyle {\begin{aligned}{\frac {di\left(t\right)}{dt}}=&\beta s\left(t\right)i\left(t\right)-\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)\\\int _{i\left(t^{*}-\tau _{i}\right)}^{i\left(t^{*}\right)}di=&\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)dt\\i\left(t^{*}\right)=&\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t-\tau _{i}\right)i\left(t-\tau _{i}\right)dt\right]{eq:cat}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8a500d717706c37e14bf29bc0311f60d2da7ab)




















































![{\displaystyle \det \left[\Delta \left(\lambda \right)\right]=\det \left[\lambda \mathbb {I} -A_{0}-\sum _{i=1}^{k}A_{i}e^{-\lambda T_{i}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af165a4947325d8223f3e6bc9dbe57c2acfbe569)



![{\textstyle \det \left[\lambda \mathbb {I} -A_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/385c1cfaf89279b436eb62e91a64e45625af1385)
![{\textstyle \det \left[\Delta \left(\lambda \right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b6401e8e0b97bad294469d0bcb08e63a3cdd426)




![{\displaystyle {\begin{aligned}\det \left[\Delta \left(\lambda \right)\right]=&\det \left[\lambda \mathbb {I} -A_{0}-A_{1}e^{-\lambda \tau _{0}}-A_{2}e^{-\lambda \tau _{i}}\right]\\=&\det \left[\left({\begin{array}{cc}\lambda &0\\0&\lambda \end{array}}\right)-\beta \left({\begin{array}{cc}-i^{*}&-s^{*}\\i^{*}&s^{*}\end{array}}\right)-\beta \left({\begin{array}{cc}i^{*}&s^{*}\\0&0\end{array}}\right)e^{-\lambda \tau _{0}}+\beta \left({\begin{array}{cc}0&0\\i^{*}&s^{*}\end{array}}\right)e^{-\lambda \tau _{i}}\right]\\=&\det \left[\left({\begin{array}{cc}\lambda +\beta i^{*}\left(1-e^{-\lambda \tau _{0}}\right)&\beta s^{*}\left(1-e^{-\lambda \tau _{0}}\right)\\\beta i^{*}\left(e^{-\lambda \tau _{i}}-1\right)&\lambda +\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\end{array}}\right)\right]\\=&\left[\lambda +\beta i^{*}\left(1-e^{-\lambda \tau _{0}}\right)\right]\left[\lambda +\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\right]-i^{*}\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\beta \left(1-e^{-\lambda \tau _{0}}\right)\\=&\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]+\beta ^{2}s^{*}i^{*}\left(e^{-\lambda \tau _{i}}-1\right)\left(1-e^{-\lambda \tau _{0}}\right)-\beta ^{2}s^{*}i^{*}\left(e^{-\lambda \tau _{i}}-1\right)\left(1-e^{-\lambda \tau _{0}}\right)\\=&\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd8f17768c479c7e3a2cbc539ed13c67fdf6f38)
![{\displaystyle {\begin{aligned}\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/757b2f6a0a8648034d3949191c4098ae1acb152f)

![{\displaystyle {\begin{aligned}\lambda +\beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf78f7b306aa827762fa0b596e14ff81918e685)








![{\displaystyle {\begin{aligned}f\left(\lambda \right)&=\lambda +\beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]\\f'\left(\lambda \right)&=1+\beta \left[\tau _{0}i^{*}e^{-\lambda \tau _{0}}-s^{*}\tau _{i}e^{-\lambda \tau _{i}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/567b36fa7c40c26cc6255397872da4c824b38e63)