Sistemas de equações diferenciais com atrasos fixos - SIRS

Anterior: Exemplo: equação diferencial com retardo | Índice: Ecologia | Próximo: Simulação e modelo de campo médio

O sistema

O exemplo a ser considerado é da biologia matemática, muitas ferramentas matemáticas utilizado na dinâmica de populações encontra-se também na dinâmica de epidemias. O objetivo deste tópico não é se aprofundar na modelagem em si, mas a utilizar como motivação para compreender melhor os sistemas de equações diferenciais com atraso baseado no artigo "Oscillations in SIRS model with distributed delays".

Uma doença do tipo SIRS é caracterizada por um tempo de infecção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{i}} e um tempo de imunidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{r}} . Isto é, um indivíduo que se infecte em um tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} vai deterministicamente se recuperar em um tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t+\tau_{i}} , tornando-se temporariamente imune por um tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{r}} . Então no instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t+\tau_{i}+\tau_{r}\equiv t+\tau_{0}} perde a imunidade tornando-se suscetível novamente. Este sistema pode ser representado por um conjunto de equações para a fração de população infecciosa (e infectada) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t\right)} e suscetível Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle s\left(t\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{s}\left(t\right)=-\beta s\left(t\right)i\left(t\right)+\beta s\left(t-\tau_{0}\right)i\left(t-\tau_{0}\right)}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{i}\left(t\right)=\beta s\left(t\right)i\left(t\right)-\beta s\left(t-\tau_{i}\right)i\left(t-\tau_{i}\right)}

Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \beta} é a taxa de contágio por indivíduo. A fração da subpopulação em recuperação (imune) é dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r\left(t\right)=1-s\left(t\right)-i\left(t\right)} . O primeiro termos em ambas as equações representa o contágio dos suscetíveis pelos infecciosos, daqui em diante muitas vezes será referido como: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c\left(t\right)=\beta s\left(t\right)i\left(t\right)} . Os segundos termos representam a recuperação ou a perda de imunidade após Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{i}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{0}} decorrido desde a infecção, respectivamente. Isto é:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{s}\left(t\right)=-c\left(t\right)+c\left(t-\tau_{0}\right)}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{i}\left(t\right)=c\left(t\right)-c\left(t-\tau_{i}\right)}

Em outras palavras, uma fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c\left(t\right)} se contagia no instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} , no instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t+\tau_{i}} ela se recupera, diminuindo os infecciosos. No instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t+\tau_{i}+\tau_{r}} ela perde a imunidade, aumentando a quantidade de suscetíveis. Estas equações exigem condições iniciais, matematicamente usualmente se fornece funções arbitrárias Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle s\left(t\right)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t\right)} no intervalo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[-\tau_{0},0\right]} . Porém de um ponto de vista epidemiológico, é razoável prover condições iniciais em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t=0} e dinâmicas complementares nos intervalos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[0,\tau_{i}\right)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[\tau_{i},\tau_{0}\right)} .

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[0,\tau_{i}\right)\rightarrow} somente contágio local. Utiliza-se as equações apenas com os primeiros termos, sem atraso.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[\tau_{i},\tau_{0}\right)\rightarrow} Transição do estágio de infeccioso para em recuperação, ou seja, retira-se apenas o segundo termo na equação da dinâmica dos suscetíveis.

E com as condições iniciais:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s\left(0\right)=1-i_{0},i\left(0\right)=i_{0},r\left(0\right)=0}

Ponto de equilíbrio

Para análise dos pontos de equilíbrio uma representação integral é uma forma melhor forma de representar o sistema, pois se fizermos algo análogo ao que foi feito em Equações diferenciais com atrasos, não será possível obter nenhuma informação sobre o ponto de equilíbrio, pois aparentemente qualquer par de valores poderia representar um ponto de equilíbrio. Para a dinâmica dos infecciosos é proposto então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\left(t\right)=c_{1}+\int_{t-\tau_{i}}^{t}c\left(u\right)du}

A interpretação é direta, integra-se sobre sobre todos os indivíduos que se contagiaram entre o tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t-\tau_{i}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} . Estes serão os infecciosos no instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} , uma vez que todos infectados anteriormente a este tempo já estarão recuperados. A constante de integração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}} a princípio é arbitrária, mas espera-se que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}=0} pois não deve haver outras fontes de infecções adicionais. Complementariamente:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-r\left(t\right)=c_{2}-\int_{t-\tau_{0}}^{t-\tau_{i}}c\left(u\right)du}

Pelo lado esquerdo, pode-se perceber ver que isto se refere a população que não está se recuperando, isto é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 1-r\left(t\right)=s\left(t\right)+i\left(t\right)} , ou seja, os infectados e suscetíveis. A integral cobre os contágios que ocorreram durante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{r}} anterior. Desta forma, esta integral fornece o número de pessoas que estão no período de recuperação, logo é razoável supor que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{2}=1} uma vez que também não há outras fontes de pessoas em recuperação. Para um estado de equilíbrio então que a fração de contagiados em um instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} qualquer é constante, pode-se escrever Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c\left(u\right)=c_{0}} . Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t_{0}\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\left(t_{0}\right) & =c_{0}\int_{t_{0}-\tau_{i}}^{t_{0}}du\\ & =c_{0}\left(t_{0}-t_{0}+\tau_{i}\right)\\ & =c_{0}\tau_{i}\end{align}}

E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle s\left(t_0\right)} , de maneira análoga:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} s\left(t_{0}\right) & =1-\int_{t_{0}-\tau_{0}}^{t_{0}-\tau_{i}}c\left(u\right)du-i\left(t_{0}\right)\\ & =1-c_{0}\int_{t_{0}-\tau_{0}}^{t_{0}-\tau_{i}}du-c_{0}\tau_{i}\\ & =1-c_{0}\left(t_{0}-\tau_{i}-t_{0}+\tau_{0}\right)-c_{0}\tau_{i}\\ & =1-c_{0}\left(-\tau_{i}+\tau_{i}+\tau_{r}\right)-c_{0}\tau_{i}\\ & =1-c_{0}\tau_{r}-c_{0}\tau_{i}\\ & =1-c_{0}\left(\tau_{r}+\tau_{i}\right)\\ & =1-c_{0}\tau_{0}\end{align}}

Uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s\left(t\right)=1-r\left(t\right)-i\left(t\right)} . Lembrando que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c\left(t\right)=\beta s\left(t\right)i\left(t\right)} , então no estado de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{0}=\beta s\left(t_{0}\right)i\left(t_{0}\right)} , denotando os pontos de equilíbrio apenas como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle s\left(t_{0}\right)=s^{*}} e ${\textstyle i\left(t_{0}\right)=i^{*}}$ , obtém-se do primeiro resultado:

{\begin{aligned}i^{*}&=\beta s^{*}i^{*}\tau _{i}\\s^{*}&={\frac {1}{\beta \tau _{i}}}\end{aligned}}

E do segundo:

{\begin{aligned}1&=1-\beta s^{*}i^{*}\tau _{0}\\1&={\frac {1}{s^{*}}}-\beta i^{*}\tau _{0}\\\beta i^{*}\tau _{0}&=\beta \tau _{i}-1\\i^{*}&={\frac {\beta \tau _{i}-1}{\beta \tau _{0}}}\end{aligned}}

Assim o ponto de equilíbrio é: ${\textstyle \left(s^{*},i^{*}\right)=\left({\frac {1}{\beta \tau _{i}}},{\frac {\beta \tau _{i}-1}{\beta \tau _{0}}}\right)}$ .

Validade da aproximação e sistema de equações sem atraso

Uma atenção especial deve ser dada a consideração de que ${\textstyle c_{1}=0}$ quando foi proposto a equação integral para ${\textstyle i\left(t\right)}$ . A formulação matemática do modelo sem atraso é usualmente escrito como:

{\begin{aligned}{\frac {ds\left(t\right)}{dt}}=&-\beta s\left(t\right)i\left(t\right)+{\frac {r\left(r\right)}{\tau _{r}}}\\{\frac {di\left(t\right)}{dt}}=&\beta s\left(t\right)i\left(t\right)-{\frac {i\left(r\right)}{\tau _{i}}}\\{\frac {dr\left(t\right)}{dt}}=&{\frac {i\left(r\right)}{\tau _{i}}}-{\frac {r\left(r\right)}{\tau _{r}}}\end{aligned}}

Integrando a equação da dinâmica de ${\textstyle i\left(t\right)}$ do sistema sem atraso, de ${\textstyle t^{*}-\tau _{i}}$ a ${\textstyle t^{*}}$ , obtém-se:

{\begin{aligned}{\frac {di\left(t\right)}{dt}}&=\beta s\left(t\right)i\left(t\right)-{\frac {i\left(t\right)}{\tau _{i}}}\\\int _{i\left(t^{*}-\tau _{i}\right)}^{i\left(t^{*}\right)}di&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\\i\left(t^{*}\right)&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau _{i}\right)-{\frac {1}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\right]{eq:tri}\end{aligned}}

Considerando no equilíbrio que ${\textstyle i\left(t^{*}\right)=i\left(t^{*}-\tau _{i}\right)}$ :

{\begin{aligned}0&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-{\frac {i^{*}}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt\\{\frac {i^{*}}{\tau _{i}}}\int _{t^{*}-\tau _{i}}^{t^{*}}i\left(t\right)dt&=\int _{t^{*}-\tau _{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt\end{aligned}}

Sendo que no equilíbrio os valores são constantes ${\textstyle i\left(t\right)=i^{*}}$ e ${\textstyle s\left(t\right)=s^{*}}$ :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{i^{*}}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}dt & =\beta s^{*}i^{*}\int_{t^{*}-\tau_{i}}^{t^{*}}dt\\ i^{*} & =\beta s^{*}i^{*}\tau_{i}{eq:siete}\end{align}}

De onde é possível obter também o mesmo ponto de equilíbrio obtido anteriormente:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} s^{*} & =\frac{1}{\beta\tau_{i}}\end{align}}

Outra formar de comparar as equações, é que para obter versão integral apresentada para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t\right)} a partir de::

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\left(t^{*}\right)=\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau_{i}\right)-\frac{1}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}i\left(t\right)dt\right]}

É é necessário que o termo entre colchete seja zerado. Isto é, considerando que no equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t^{*}-\tau_{i}\right)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t^{*}-\tau_{i}\right)} sejam constantes:

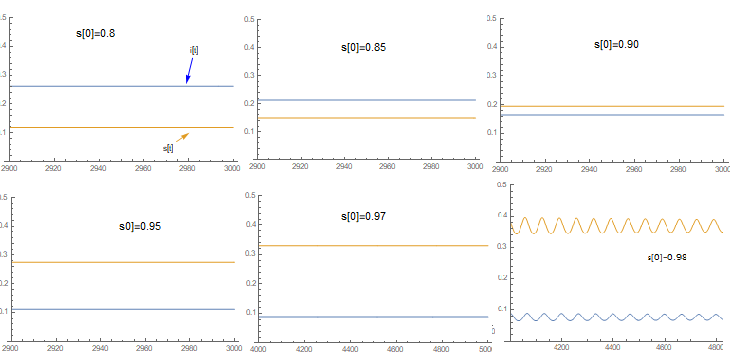
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\left(t^{*}-\tau_{i}\right) & =\frac{1}{\tau_{i}}\int_{t^{*}-\tau_{i}}^{t^{*}}i\left(t\right)dt\\ i\left(t^{*}-\tau_{i}\right) & =i\left(t^{*}\right)\end{align}}

Desta forma a condição imposta anteriormente é recuperada. Agora percebe-se que o ponto de equilíbrio é independente das condições iniciais, depende apenas dos parâmetros escolhidos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \beta,\tau_{i}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{r}} . Por exemplo, resolvendo numericamente o sistema de equações diferenciais proposto, com os parâmetros Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \beta=0.4} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{i}=5} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{r}=50} , e condições iniciais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(s_{0},i_{0}\right)=\left(0.5,0.5\right)} , o sistema atinge o equilíbrio precisamente nos pontos calculados.

Solução numérica do sistema de equações diferenciais sem atraso obtido via Mathematica.

Além disto, pode-se verificar que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i^{*}\approx0.45} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c^{*}=\beta s^{*}i^{*}\tau_{i}\approx0.45} , concordando com nossos cálculos analíticos. Isto implica que no equilíbrio, a população total infecciosa em um instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} é sempre dada inteiramente pelos que foram infectados durante um período anterior Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t-\tau_{i}} , ou seja, a área dada pelo retângulo de largura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{i}} e altura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \beta s^{*}i^{*}} , uma vez que no equilíbrio as frações Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t\right)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle s\left(t\right)} são constantes. Estes resultados concordam com a suposição de que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}=0} .

Porém tentando o mesmo procedimento para a equação com atraso, obtém-se:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{di\left(t\right)}{dt}= & \beta s\left(t\right)i\left(t\right)-\beta s\left(t-\tau_{i}\right)i\left(t-\tau_{i}\right)\\ \int_{i\left(t^{*}-\tau_{i}\right)}^{i\left(t^{*}\right)}di= & \int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt-\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t-\tau_{i}\right)i\left(t-\tau_{i}\right)dt\\ i\left(t^{*}\right)= & \int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt+\left[i\left(t^{*}-\tau_{i}\right)-\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t-\tau_{i}\right)i\left(t-\tau_{i}\right)dt\right]{eq:cat}\end{align}}

Utilizando a consideração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t^{*}\right)=i\left(t^{*}-\tau_{i}\right)} , é possível obter apenas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\left(t^{*}\right)=i\left(t^{*}\right)} . Para recuperar a equação original seria necessário que, de modo análogo a equação sem atraso, a seguinte igualdade fosse válida:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\left(t^{*}\right)=\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt}

Isto é, de modo análogo ao caso anterior, que no equilíbrio a fração de infecciosos em um tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} seja dado inteiramente pelos que foram contagiados em um tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t-\tau_{i}} . Porém neste caso qualquer par de pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(i^{*},s^{*}\right)} poderia consistir em um ponto de equilíbrio para um conjunto de parâmetros Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left\{ \beta,\tau_{i},\tau_{r}\right\}} qualquer. A dependência se torna das condições iniciais. Utilizando por exemplo condições iniciais constantes como frequentemente é utilizado na literatura de equações com atraso, a própria condição inicial se torna um ponto de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i_{0}=i^{*}} . Pode-se pensar que desta fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i^{*}} de infecciosos , a cada instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} , uma quantidade de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c=\beta i_{0}s_{0}} de infecciosos são curados, porém outra quantidade igual Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c} de suscetíveis são infectados, mantendo a taxa de variação zerada e a quantidade total de infecciosos constante. Assim sendo, pensando em situações reais, para um instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} , há quantidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i_{c}=i_{0}-c} da fração que permanece infecciosa mesmo após Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_i} , que soma-se aos novos infectados, mantendo a fração constante. Isto é, para a equação:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\left(t\right)=c_{1}+\int_{t^{*}-\tau_{i}}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt}

Então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}\neq0} . Para retirar esta constante, pode-se pensar que é como se no equilíbrio precisasse de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=\frac{i_{0}}{c}=\frac{i_{0}}{\beta i_{0}s_{0}}=\frac{1}{\beta s_{0}}} tempo para que uma pessoa infecciosa se curasse, ao invés de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{i}} . Pois após Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle n} tempo toda a população Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i_{0}} terá sido substituída por uma nova população infecciosa isto é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i_{0}-nc=0} , uma vez que a cada instante ${\textstyle t=n}$ tem-se que uma fração ${\textstyle c}$ da população suscetível sendo infectada, e outra fração $c$ da população infecciosa que se recuperou pois foi infectada em um instante anterior ${\textstyle t-\tau _{i}}$ . . Reescrevendo a integral com este novo limite

i\left(t\right)=\int _{t^{*}-n}^{t^{*}}\beta s\left(t\right)i\left(t\right)dt=\beta s^{*}i^{*}n={\frac {\beta s^{*}i^{*}}{\beta s_{0}}}=i^{*}

Uma vez que ${\textstyle s_{0}=s^{*}}$ para estas condições iniciais. Além disto, a expressão para $n$ é análoga a equação encontrada para o ponto de equilíbrio do sistema sem atraso, isto é ${\textstyle \tau _{i}=1/\beta s^{*}}$ . Toda discussão foi feita para condições iniciais constantes, quando se utiliza o método proposto, a análise torna-se mais complicada, mas ainda é notável que o ponto de equilíbrio depende das condições iniciais.Utilizando o conjunto de parâmetros ${\textstyle \beta =0.4}$ , ${\textstyle \tau _{i}=5}$ e ${\textstyle \tau _{r}=50}$ , para diferentes valores iniciais é possível obter:

Solução em equilíbrio do sistema de equações diferenciais com atraso para diferentes valores iniciais de infecciosos.

Pode-se notar que aproximadamente:

${\textstyle i_{0}=}$	${\textstyle \tau _{i}c\approx }$	${\textstyle i^{*}\approx }$
${\textstyle 0.20}$	${\textstyle 0.06}$	${\textstyle 0.26}$
${\textstyle 0.15}$	${\textstyle 0.06}$	${\textstyle 0.21}$
${\textstyle 0.10}$	${\textstyle 0.06}$	${\textstyle 0.16}$
${\textstyle 0.05}$	${\textstyle 0.06}$	${\textstyle 0.11}$

Lembrando da integral proposta para a condição de equilíbrio condição de equilíbrio:

{\begin{aligned}i\left(t\right)&=c_{1}+\int _{t^{*}-\tau _{i}}^{t^{*}}c\left(t\right)dt{eq:veinte}\end{aligned}}

Novamente ${\textstyle c_{1}\neq 0}$ , mais especificamente $i_{0}=c_{1}$ . Este resultado faz sentido, pois de acordo com o procedimento proposto, não há momento em que os infecciosos iniciais ${\textstyle i_{0}}$ se recuperam. Durante o tempo ${\textstyle 0\leq t<\tau _{i}}$ uma fração da população se infecta, e então esta mesma fração começa a se recuperar após ${\textstyle t>\tau _{i}}$ , mas os infecciosos iniciais, nunca se recuperam, funcionando como fontes permanentes de infecção. Outra forma de comparar, é que olhando o conjunto de equações diferenciais originais o termo responsável pela recuperação dos infecciosos no instante ${\textstyle t}$ depende da quantidade total de infecciosos no próprio instante ${\textstyle t}$ . No conjunto de equações com atraso, é a fração da população da população que foi contagiada em um instante anterior. Ou seja, uma fração da população que se infectou em um instante ${\textstyle t}$ , é a mesma que se recuperara em um instante posterior ${\textstyle t+\tau _{i}}$ , porém a quantidade inicial de infecciosos não se contagiou em nenhum momento desta ’linha do tempo', então também não se recuperam em nenhum momento.

Porém ainda que ${\textstyle c_{1}\neq 0}$ , quanto mais próximo a população inicial de infecciosos for de ${\textstyle 0}$ , melhor será aproximação, Por isso a análise em torno do ponto de equilíbrio, e o próprio ponto de equilíbrio se torna uma aproximação válida apenas quando é adotado valores próximos de ${\textstyle 0}$ para ${\textstyle i_{0}}$ .

Análise do ponto de equilíbrio

Obtendo a equação transcendental

Aplicando então uma perturbação nos pontos de equilíbrios, isto é: ${\textstyle s\left(t\right)=s^{*}+x\left(t\right)}$ e ${\textstyle i}$ ${\textstyle \left(t\right)=i^{*}+y\left(t\right)}$ pode-se obter uma aproximação linear em torno do ponto de equilíbrio (uma observação é que o teste utilizando os limites leva a uma indeterminação, uma vez que não há termo linear). Então analisando o termo que chamamos de contágios:

{\begin{aligned}c\left(t\right)&=\beta s\left(t\right)i\left(t\right)\\{\frac {c\left(t\right)}{\beta }}&=\left(s^{*}+x\left(t\right)\right)\left(i^{*}+y\left(t\right)\right)\\&=s^{*}i^{*}+i^{*}x\left(t\right)+s^{*}y\left(t\right)+x\left(t\right)y\left(t\right)\end{aligned}}

Ignorando os termos não lineares e denotando ${\textstyle f\left(t\right)=f}$ e ${\textstyle f\left(t-\tau \right)=f_{\tau }}$ :

{\begin{aligned}{\frac {c}{\beta }}&=s^{*}i^{*}+i^{*}x+s^{*}y\end{aligned}}

Tem-se então:

{\begin{aligned}{\frac {\dot {x}}{\beta }}=&-\left(s^{*}i^{*}+i^{*}x+s^{*}y\right)+\left(s^{*}i^{*}+i^{*}x_{\tau _{0}}+s^{*}y_{\tau _{0}}\right)\\&=-\left(i^{*}x+s^{*}y\right)+\left(i^{*}x_{\tau _{0}}+s^{*}y_{\tau _{0}}\right)\end{aligned}}

E:

{\begin{aligned}{\frac {\dot {y}}{\beta }}=&-\left(s^{*}i^{*}+i^{*}x_{\tau _{i}}+s^{*}y_{\tau _{i}}\right)+\left(s^{*}i^{*}+i^{*}x+s^{*}y\right)\\&=\left(i^{*}x+s^{*}y\right)-\left(i^{*}x_{\tau _{i}}+s^{*}y_{\tau _{i}}\right)\end{aligned}}

O sistema linearizado em torno do ponto de equilíbrio é então:

{\begin{aligned}{\frac {\dot {x}}{\beta }}&=-\left(i^{*}x+s^{*}y\right)+\left(i^{*}x_{\tau _{0}}+s^{*}y_{\tau _{0}}\right)\\{\frac {\dot {y}}{\beta }}&=+\left(i^{*}x+s^{*}y\right)-\left(i^{*}x_{\tau _{i}}+s^{*}y_{\tau _{i}}\right)\end{aligned}}

Reescrevendo matricialmente:

\left({\begin{array}{c}{\dot {x}}\\{\dot {y}}\end{array}}\right)=\beta \left({\begin{array}{cc}-i^{*}&-s^{*}\\i^{*}&s^{*}\end{array}}\right)\left({\begin{array}{c}x\\y\end{array}}\right)+\beta \left({\begin{array}{cc}i^{*}&s^{*}\\0&0\end{array}}\right)\left({\begin{array}{c}x_{\tau _{0}}\\y_{\tau _{0}}\end{array}}\right)+\beta \left({\begin{array}{cc}0&0\\-i^{*}&-s^{*}\end{array}}\right)\left({\begin{array}{c}x_{\tau _{i}}\\y_{\tau _{i}}\end{array}}\right)

Ou ainda:

{\dot {\boldsymbol {x}}}\left(t\right)=A_{0}{\boldsymbol {x}}+A_{1}{\boldsymbol {x}}\left(t-\tau _{0}\right)+A_{2}{\boldsymbol {x}}\left(t-\tau _{i}\right)

A equação característica para um sistema do tipo:

{\dot {\boldsymbol {x}}}\left(t\right)=A_{0}{\boldsymbol {x}}\left(t\right)+\sum _{i=1}^{k}A_{i}{\boldsymbol {x}}\left(t-T_{i}\right)

É dado por:

\det \left[\Delta \left(\lambda \right)\right]=\det \left[\lambda \mathbb {I} -A_{0}-\sum _{i=1}^{k}A_{i}e^{-\lambda T_{i}}\right]

A função ${\textstyle \Delta \left(\lambda \right)}$ é chamada de quase-polinômio característico. Como de costume, se para para todo ${\textstyle \lambda \in \mathbb {C} }$ , for ${\textstyle Re\left(\lambda \right)<0}$ o sistema é assintoticamente estável.

Detalhes:

Se não houver atraso, a equação é reduzida a ${\textstyle \det \left[\lambda \mathbb {I} -A_{0}\right]}$ . Como para achar as raízes deve-se fazer ${\textstyle \det \left[\Delta \left(\lambda \right)\right]=0}$ , obtém-se o resultado tradicional.
Se houver apenas uma equação, e não um sistema, então os termos ${\textstyle A_{j}}$ serão constantes e não uma matrizes. Substituindo ${\textstyle x\left(t\right)=ce^{\lambda t}}$ :

{\begin{aligned}\lambda ce^{\lambda t}&=A_{0}ce^{\lambda t}+\sum _{i=1}^{k}A_{i}ce^{\lambda t}e^{-\lambda T_{i}}\\\lambda &=A_{0}+\sum _{i=1}^{k}A_{i}e^{-\lambda T_{i}}\end{aligned}}

Então:

\lambda -A_{0}-\sum _{i=1}^{k}A_{i}e^{-\lambda T_{i}}=0

Obtém-se o quase-polinômio característico proposto pro sistema conforme. Dessa forma, a equação transcendental característica para o sistema que estamos interessados é:

{\begin{aligned}\det \left[\Delta \left(\lambda \right)\right]=&\det \left[\lambda \mathbb {I} -A_{0}-A_{1}e^{-\lambda \tau _{0}}-A_{2}e^{-\lambda \tau _{i}}\right]\\=&\det \left[\left({\begin{array}{cc}\lambda &0\\0&\lambda \end{array}}\right)-\beta \left({\begin{array}{cc}-i^{*}&-s^{*}\\i^{*}&s^{*}\end{array}}\right)-\beta \left({\begin{array}{cc}i^{*}&s^{*}\\0&0\end{array}}\right)e^{-\lambda \tau _{0}}+\beta \left({\begin{array}{cc}0&0\\i^{*}&s^{*}\end{array}}\right)e^{-\lambda \tau _{i}}\right]\\=&\det \left[\left({\begin{array}{cc}\lambda +\beta i^{*}\left(1-e^{-\lambda \tau _{0}}\right)&\beta s^{*}\left(1-e^{-\lambda \tau _{0}}\right)\\\beta i^{*}\left(e^{-\lambda \tau _{i}}-1\right)&\lambda +\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\end{array}}\right)\right]\\=&\left[\lambda +\beta i^{*}\left(1-e^{-\lambda \tau _{0}}\right)\right]\left[\lambda +\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\right]-i^{*}\beta \left(e^{-\lambda \tau _{i}}-1\right)s^{*}\beta \left(1-e^{-\lambda \tau _{0}}\right)\\=&\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]+\beta ^{2}s^{*}i^{*}\left(e^{-\lambda \tau _{i}}-1\right)\left(1-e^{-\lambda \tau _{0}}\right)-\beta ^{2}s^{*}i^{*}\left(e^{-\lambda \tau _{i}}-1\right)\left(1-e^{-\lambda \tau _{0}}\right)\\=&\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]\end{aligned}}

Para encontrar as raízes

{\begin{aligned}\lambda ^{2}+\lambda \beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]&=0\end{aligned}}

Esta equação é chamada de equação característica transcendental. Uma raiz é ${\textstyle \lambda =0}$ , e a outra pode ser obtida a partir de:

{\begin{aligned}\lambda +\beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]&=0\end{aligned}}

Como uma raiz é ${\textstyle \lambda _{1}=0}$ , se ${\textstyle \lambda _{2}>0}$ há um equilíbrio instável próximo ao ponto de equilíbrio.

Observações:
- Equação transcendental: equação que contém uma função transcendental da variável que deve ser resolvida.
- Função transcendental: função que não satisfaz uma equação polinomial, em contraste com uma função algébrica, isto é, transcende a álgebra”. Um exemplo é a função exponencial.
- Função algébrica: função que pode ser definida como a raiz de uma equação polinomial.

Soluções aproximadas são obtidas por métodos gráficos conforme feito anteriormente para soluções reais em Equações diferenciais com atrasos, ou até simplesmente observando o gráfico. Mas neste caso será utilizado algoritmos.

Obtendo as raízes da equação transcendental

Método de Newton

Também conhecido como método de Newton-Raphson, aproxima a função com uma linha. Esta linha atravessa o ponto ${\textstyle \left(x_{i},f\left(x_{i}\right)\right)}$ e tem inclinação igual a derivada da própria função. Matematicamente isto é:

{\begin{aligned}f'\left(x_{i}\right)=&{\frac {y_{i+1}-f\left(x_{i}\right)}{x_{i+1}-x_{i}}}\\x_{i+1}=&x_{i}+{\frac {\left(y_{i+1}-f\left(x_{i}\right)\right)}{f'\left(x_{i}\right)}}\end{aligned}}

Então encontra-se o ${\textstyle x}$ que atravessa o eixo e o utiliza como uma nova tentativa. Ou seja o segundo ponto sobre a reta é ${\textstyle \left(x_{i+1},0\right)}$ , então:

{\begin{aligned}x_{i+1}=&x_{i}-{\frac {f\left(x_{i}\right)}{f'\left(x_{i}\right)}}\end{aligned}}

Para estender o método para o plano complexo, basta substituir variável real ${\textstyle x}$ por uma variável complexa ${\textstyle z=x+yi}$ . A partir disto, o loop é repetido.

Aplicando o método

Então sendo:

{\begin{aligned}f\left(\lambda \right)&=\lambda +\beta \left[s^{*}\left(e^{-\lambda \tau _{i}}-1\right)-i^{*}\left(e^{-\lambda \tau _{0}}-1\right)\right]\\f'\left(\lambda \right)&=1+\beta \left[\tau _{0}i^{*}e^{-\lambda \tau _{0}}-s^{*}\tau _{i}e^{-\lambda \tau _{i}}\right]\end{aligned}}

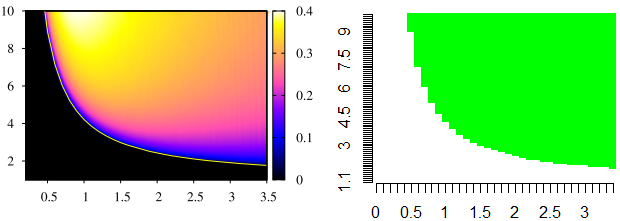
Foi utilizado um algoritmo em Python para buscar as raízes complexas. O gráfico original é ${\textstyle R_{0}\times {\frac {\tau _{r}}{\tau _{i}}}}$ . Onde ${\textstyle R_{0}=\beta \tau _{i}}$ é chamado de taxa de reprodução básica. Para facilitar foi escolhido denotar ${\textstyle R_{1}={\frac {\tau _{r}}{\tau _{i}}}}$ . Com poucas manipulações é possível mostrar que:

{\begin{aligned}\tau _{i}=&{\frac {R_{0}}{\beta }}\\\tau _{r}=&{\frac {R_{1}R_{0}}{\beta }}\end{aligned}}

Assim para um ${\textstyle \beta }$ constante pode-se variar apenas ${\textstyle R_{0}}$ e ${\textstyle R_{1}}$ . Deste modo o algoritmo proposto busca a existência de raízes com parte real positiva, isto é, o conjunto de equações apresenta comportamento instável na proximidade do ponto de equilíbrio. Esta busca ocorre para cada par de valores ${\textstyle \left(R_{1},R_{0}\right)}$ na malha formada por ${\textstyle R_{0}\times R_{1}}$ , onde ${\textstyle 1<R_{0}<10}$ e ${\textstyle 0\leq R_{1}<3.5}$ , com intervalos de ${\textstyle \Delta =0.1}$ . Especificamente em cada par de valores é executado o algoritmo de Newton-Raphson com o chute inicial partindo de cada ponto possível do plano complexo dentro da região delimitada por ${\textstyle -1\leq \mathbb {R} \left(\lambda \right),\mathbb {I} \left(\lambda \right)<1}$ , com espaçamento entre os pontos de $\Delta =0.1$ . Isto ocorre enquanto nenhuma raiz com parte real positiva seja encontrada, além disso, é realizada no máximo $N=10^{7}$ tentativas de aproximação, e é considerado $f\left(x\right)=0$ se $\left|f\left(x\right)\right|<10^{-12}$ .

A esquerda a imagem original retirada do artigo. A região preta são soluções sem oscilação e a colorida onde há a presença de oscilações. A direita a imagem obtida através do algoritmo proposto onde a região verde indica que foi encontrado autovalores positivos.

Algoritmos

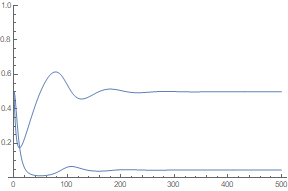
O conjunto de equações diferenciais sem atraso pode ser solucionado via Mathematica:

tmax = 400; b = 0.4; ti = 5; tr = 5;
sol = NDSolve[{
    s'[t] == -b*s[t]*i[t] + r[t]/tr,
    i'[t] == +b*s[t]*i[t] - i[t]/ti,
    r'[t] == i[t]/ti - r[t]/tr,
    s[0] == 0.5, i[0] == 0.5, r[0] == 0},
   {s, i, r}, {t, 0, 500}];
Plot[{i[t] /. sol, s[t]} /. sol, {t, 0, 500}, PlotRange -> {0., 1.}]

O sistema de equações diferenciais com atraso pode ser pode ser solucionado via Python utilizando o método de Euler conforme proposto :

import matplotlib.pyplot as plt
import numpy as np
#Função para resolver o sistema de equações diferenciais
def sistema(R0,R1):
    #Parâmetro R0=b.ti
    #Parâmetro R1=tr/ti
    #Parâmetros da dinâmica
    b =4
    ti=R0/b
    tr=R1*R0/b
    to=ti+tr
    # Listas para guardar a evolução do sistema
    s=[]
    i=[]
    d=0.001 #Passo para o método de Euler
    #Primeira parte:
    N1=int(ti/d)     #Quantidade de passos
    i.append(1e-16)  #Condição inicial de inectado i0
    s.append(1-i[0]) #Condição inicial de suscetíveis s0=1-i0
    #Resolve o sistema Usando o método de Euler
    for k in range(N1):
        s.append(s[k]+d*(-b*s[k]*i[k]))
        i.append(i[k]+d*(b*s[k]*i[k]))
    #Segunda parte
    N2=int(to/d)
    for k in range(N1,N2):
        s.append(s[k]+d*(-b*s[k]*i[k]))
        i.append(i[k]+d*(b*s[k]*i[k]-b*s[k-int(ti/d)]*i[k-int(ti/d)]))
    #Terceira parte
    N3=int(1800/d)
    for k in range(N2,N3):
        s.append(s[k]+d*(-b*s[k]*i[k]+b*s[k-int(to/d)]*i[k-int(to/d)]))
        i.append(i[k]+d*(+b*s[k]*i[k]-b*s[k-int(ti/d)]*i[k-int(ti/d)]))

O sistema também pode ser resolvido via Mathematica:

b = 0.8; ti = 5; to = 20;
ci1 = NDSolve[{
    s1'[t] == -b*s1[t]*i1[t],
    i1'[t] == +b*s1[t]*i1[t],
    s1[0] == 0.99, i1[0] == 0.01},
   {s1, i1}, {t, 0, ti}];
ci2 = NDSolve[{
    s2'[t] == -b*s2[t]*i2[t],
    i2'[t] == +b*s2[t]*i2[t] - b*s2[t - ti]*i2[t - ti],
    s2[t /; t <= ti] == s1[t] /. ci1, 
    i2[t /; t <= ti] == i1[t] /. ci1},
   {s2, i2}, {t, 0, to}];
sol = NDSolve[{
    s'[t] == -b*s[t]*i[t] + b*s[t - to]*i[t - to],
    i'[t] == +b*s[t]*i[t] - b*s[t - ti]*i[t - ti],
    s[t /; t <= to] == s2[t] /. ci2, i[t /; t <= to] == i2[t] /. ci2},
   {s, i}, {t, 0, 300}];
Plot[{i[t] /. sol, s[t] /. sol}, {t, 0, 300}, PlotRange -> {0., 1.}]

O código abaixo foi escrito em Python e é responsável por buscas raízes complexas com a parte real positiva na equação transcendental discutida anteriormente.

#Código para resolver a equação transcendental
def raizes():
    sol=np.zeros((35,90)) # Matriz para guardar as raízes
    err=1e-12             # Erro admitido   
    sy=0
    for R0 in np.arange(1,10,0.1):      #Percorrer os valores RO=b.
        print(str(100*(sy+1)/90)+"%")
        sx=0
        for R1 in np.arange(0,3.5,0.1): #Percorrer os valores R1=tr/ti
            #Parâmetros da dinâmica
            b =4
            ti=R0/b
            tr=R1*R0/b
            to=ti+tr
            #Pontos de equilíbrio
            io=(b*ti-1)/(b*to)
            so=1/(b*ti)
            #Matriz das raízes para os parâmetros atuais
            r=np.zeros((20, 20))
            #Os chutes iniciais serão pontos dentro da malha [-1,1] em 2D
            m=0
            for a in np.arange(-1,1,0.1):
                n=0
                for y in np.arange(-1,1,0.1):
                    i=y*1j
                    x=a+i  # Ponto inicial
                    N=10000000 # Quantidade máxima de aproximações
                    #Valor da função para o chute inicial
                    f=x+b*(so*(np.power(np.e,-x*ti)-1)-io*(np.power(np.e,-x*to)-1))
                    for k in range(N):
                        if (k==N-2):
                            print("!") #Indicando que chegou no último passo sem achar a raízs
                        if (abs(f)<err):
                            break        # Se chou a raíz, do loop
                        try:
                            f =x+b*(so*(np.power(np.e,-x*ti)-1)-io*(np.power(np.e,-x*to)-1))
                            df=1+b*(to*io*np.power(np.e,-x*to)-ti*so*np.power(np.e,-x*ti))
                            nx=x-f/df        # Próximo chute
                            x=nx
                        except:
                            print(str(R0)+","+str(R1))
                            break
                    if(abs(np.real(x))<err):   # A raíz é zero
                        r[m,n]=0
                    elif (np.real(x)>0):        # Raíz positiva
                        r[m,n]=1
                        break
                    else:
                        r[m,n]=-1               # Raíz negativa
                    n=n+1
                else:        # Quando acabar o loop interno
                    m=m+1
                    continue # Continua
                break        # Se o loop interno foi encerrado antes da hora, encerra o externo
            res=[]        
            for i in range(20):
                res.append(max(r[i]))
            sol[sx,sy]=max(res)                 # Se houve raíz positiva, obtém.
            sx=sx+1
        sy=sy+1
    #Registra
    f = open("raizes.dat", "w")
    for i in sol:
         for j in i:
             f.write(str(j)+"	")
         f.write("\n")
    f.close()
raizes()

A partir dos dados gerados com o código anterior, é possível visualizá-los em R com o seguinte código:

library('tseries')      #Bibliotea pra ler matriz
library('plot.matrix')  #Biblioteca pra plotar matriz

m <- read.matrix( "Raizes.dat") #Os dados são lidos no formato de matriz
m<-t(m)                         # São feitas algumas correções devido à ordem que os dados são gravados
m <-m[90:2, 1:35]
rownames(m) <- (99:11)/10       #Ajusta-se os nomes das linhas e colunas
colnames(m) <- (0:34)/10
#E plota-se
plot(m, col=c('black', 'white', 'green'), breaks=c(-2, -0.25,0.25, 2), xlab='R1', ylab='R0',main='Raizes',border=NA)

Principais materiais utilizados

Oscillations in SIRS model with distributed delays (S. Gonçalves e outros, The European Physical Journal B)
Root finding algorithms (Eugeniy E. Mikhailov, Faculdade de William e Mary)
Stability and stabilization of time-delay systems ( Gerhard Manfred Schoen ,Instituto Federal de Tecnologia de Zurique)