Análise de estabilidade de equações diferenciais lineares atrasadas

Anterior: Métodos de Lyapunov | Índice: Ecologia | Próximo: Sistemas de equações diferenciais com atrasos fixos - SIRS

Analisar a estabilidade local de equações diferenciais atrasadas é mais desafiador que realizar a mesma análise para equações diferenciais ordinárias. Isto ocorre devido a dimensionalidade infinita do sistema. Por exemplo considerando uma equação diferencial linear atrasada simples:

$${\frac {dy}{dt}}=\alpha y_{\tau }$$

Onde ${\textstyle y_{t}\equiv y\left(t-1\right)}$, só há um único ponto de equilíbrio em ${\textstyle y=0}$. Para equações diferenciais ordinárias do tipo:

$$a_{n}y^{\left(n\right)}+a_{n-1}y^{\left(n-1\right)}+\dots +a_{1}y^{'}+a_{0}y=0$$

Assumindo que as soluções vão ser da forma ${\textstyle y\left(t\right)=Ce^{\lambda t}}$, pode-se substituir:

$${\begin{aligned}Ce^{\lambda t}\left(a_{n}\lambda ^{n}+a_{n-1}\lambda ^{n-1}+\dots +a_{1}\lambda +a_{0}\right)&=0\\a_{n}\lambda ^{n}+a_{n-1}\lambda ^{n-1}+\dots +a_{1}\lambda +a_{0}\end{aligned}}$$

Então este é o polinômio característico. E sua solução nos dá a solução para a equação diferencial. Por exemplo:

$$y'-\alpha y=0\rightarrow \lambda =\alpha$$

Logo ${\textstyle y\left(t\right)=Ce^{\alpha t}}$. Esta solução pode ser conferida resolvendo diretamente esta EDO simples:

$$\int {\frac {dy}{y}}=\int \alpha dt\rightarrow y=Ce^{\alpha t}$$

Agora supondo uma solução análoga ${\textstyle y\left(t\right)=Ce^{\lambda t}}$ para a equação com atraso:

$${\frac {dy}{dt}}={\frac {d}{dt}}\left(Ce^{\lambda t}\right)=\lambda Ce^{\lambda t}$$

E

$$y\left(t-1\right)=Ce^{\lambda \left(t-1\right)}=Ce^{\lambda t}e^{-\lambda }$$

Então a equação característica é:

$${\begin{aligned}y'-\alpha y_{\tau }&=0\\\lambda Ce^{\lambda t}-\alpha Ce^{\lambda t}e^{-\lambda }&=0\\\lambda -\alpha e^{-\lambda }&=0\end{aligned}}$$

Para as equações diferenciais ordinárias havia um polinômio e o teorema fundamental da álgebra permitia dizer quantas raízes esperar. Porém para as equações diferenciais atrasadas, não há teorema algum sobre a quantidade de raízes, este número poderia inclusive ser infinito. Como exemplo, pode-se considerar soluções reais e complexas separadamente conforme será visto na sequência.

Solução real

Supondo que a solução é real, pode-se plotar ${\textstyle z_{1}=\lambda }$ e ${\textstyle z_{2}=\alpha e^{-\lambda }}$ separadamente, e então e procurar por intersecções. Isto é, quando os dois termos possuem o mesmo valor para um mesmo ${\textstyle \lambda }$, pois consequentemente então ${\textstyle \lambda -\alpha e^{-\lambda }=0}$. Se ${\textstyle \alpha >0}$, há uma única intersecção, onde ${\textstyle \lambda >0}$, então ${\textstyle y=Ce^{\lambda t}}$ aumenta exponencialmente ao infinito quando ${\textstyle t\rightarrow \infty }$. Desta forma, o ponto de equilíbrio é instável.

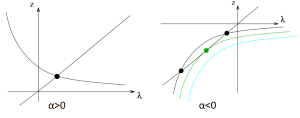
A esquerda o gráfico gerado para um valor qualquer em que $\alpha >0$, e a direita para três valores em que $\alpha <0$, especificamente $\alpha _{c}<\alpha <0$ em preto, $\alpha =\alpha _{c}$ em verde, e $\alpha <\alpha _{c}$ em azul.

Se ${\textstyle \alpha <0}$ pode haver 2 intersecções ${\textstyle \left(\alpha _{c}<\alpha \right)}$, 1 intersecção o ${\textstyle \left(\alpha _{c}=\alpha \right)}$ ou nenhuma intersecção ${\textstyle \left(\alpha <\alpha _{c}\right)}$. Para identificar qual é este ponto crítico $\alpha _{c}$, basta perceber que neste ponto a reta ${\textstyle z_{1}}$ é tangente à curva ${\textstyle z_{2}}$ no ponto ${\textstyle \left(\lambda _{c},z_{c}\right)}$. Logo, a inclinação de ambos deve ser a mesma, ${\textstyle m_{1}=m_{2}}$. A inclinação da reta ${\textstyle z_{1}}$ é simplesmente ${\textstyle m_{1}=1}$. Então a inclinação da curva também deve ser:

$$m_{2}={\frac {dz_{2}}{d\lambda }}|\lambda _{c}=-\alpha _{c}e^{-\lambda _{c}}=1$$

$$\alpha _{c}=-e^{\lambda _{c}}$$

Substituindo a constante $\alpha _{c}$ em ${\textstyle z_{2}}$:

$$z_{c}=-e^{\lambda _{c}}e^{-\lambda _{c}}=-1$$

Pode-se obter agora ${\textstyle \lambda _{c}}$ a partir da reta ${\textstyle z_{1}}$, ${\textstyle z_{c}=-1=\lambda _{c}}$. Dessa forma o valor crítico é então ${\textstyle \alpha _{c}=-e^{-1}}$. Logo, se ${\textstyle \alpha \in \left[\alpha _{c}0\right]}$, então as raízes da equação característica são reais e negativas e a solução exponencial associada decai para ${\textstyle 0}$ com o tempo. As raízes ${\textstyle \lambda }$ também são chamadas de autovalores, termo que será empregado daqui em diante.

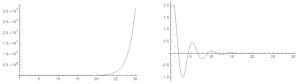
A esquerda a solução para ${\textstyle \alpha =1>0}$ e a direita para ${\textstyle \alpha _{c}\leq \alpha =-1<0}$, considerando como condição inicial ${\textstyle y_{0}=2}$.

Para ${\textstyle \alpha <\alpha _{c}}$, não há decaimento ou crescimento exponencial nos componentes da solução, para isto vamos analisar as soluções complexas. As soluções podem ser obtidas numericamente via Mathematica:

sol = NDSolve[{y'[t] == -2.0*y[t - 1], y[t /; t <= 1] == 2}, y, {t, 0, 30];
Plot[y[t] /. sol, {t, 0, 30}, PlotRange -> All]

Solução Complexa

Substituindo então ${\textstyle \lambda =\lambda _{r}+i\lambda _{i}}$, na equação característica, obtém-se:

$${\begin{aligned}\lambda -\alpha e^{-\lambda }&=0\\\lambda &=\alpha e^{-\lambda }\\\lambda _{r}+i\lambda _{i}&=\alpha e^{\left[-\lambda _{r}-i\lambda _{i}\right]}\\\lambda _{r}+i\lambda _{i}&=\alpha e^{-\lambda _{r}}e^{-i\lambda _{i}}\\\left[\lambda _{r}\right]+i\left[\lambda _{i}\right]&=\left[\alpha e^{-\lambda _{r}}\cos \lambda _{i}\right]+i\left[\alpha e^{-\lambda _{r}}\sin \left(-\lambda _{i}\right)\right]\end{aligned}}$$

Logo:

$${\begin{aligned}\lambda _{r}&=+\alpha e^{-\lambda _{r}}\cos \lambda _{i}\\\lambda _{i}&=-\alpha e^{-\lambda _{r}}\sin \lambda _{i}\end{aligned}}$$

Calculando a razão entre os termos:

$${\frac {\lambda _{r}}{\lambda _{i}}}={\frac {+\alpha e^{-\lambda _{r}}\cos \lambda _{i}}{-\alpha e^{-\lambda _{r}}\sin \lambda _{i}}}=-\cot \left(\lambda _{i}\right)$$

Então utilizando ${\textstyle \lambda _{i}}$ como parâmetro, pode-se obter equações paramétricas para ${\textstyle \lambda _{r}}$ e ${\textstyle \alpha }$:

$${\begin{aligned}\lambda _{r}&=-\cot \left(\lambda _{i}\right)\lambda _{i}\\\alpha &=-{\frac {\lambda _{i}}{\exp \left(\lambda _{i}\cot \left(\lambda _{i}\right)\right)\sin \lambda _{i}}}\end{aligned}}$$

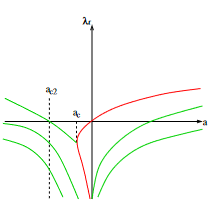
Soluções das equações paramétricas. Em vermelho o caso especial quando $\lambda _{i}=0$.

Por conta da periodicidade das funções trigonométricas, muitas curva são traçadas quando varía-se ${\textstyle \lambda _{i}}$ entre ${\textstyle -\infty }$ e ${\textstyle +\infty }$. Além, disto para ${\textstyle \lambda =\lambda _{r}}$ então ${\textstyle \lambda _{i}=0}$, desta forma pode-se plotar diretamente ${\textstyle \alpha \left(\lambda _{r}\right)}$:

$$\alpha =\lambda _{r}e^{\lambda _{r}}$$

Utilizando o Geogebra, isto pode ser feito realizando cada entrada manualmente:

-x cotg(x)
d(x) = (-x)/(e^(x cotg(x)) sen(x))
Curva(d(u), c(u), u, -60 , 60)
x = y e^y

A solução geral é ${\textstyle y\left(t;a\right)=\sum _{c}e^{\lambda _{n}t}}$, onde o somatório é sobre todos os valores de ${\textstyle \lambda _{n}}$ para um dado parâmetro ${\textstyle \alpha }$, então o estado de equilíbrio é estável para valores de ${\textstyle \alpha }$ em que todos os autovalores tem valores reais negativos. Ou seja, para valores entre ${\textstyle \alpha _{c2}}$ e o eixo ${\textstyle \alpha =0}$. pois para ${\textstyle \alpha >0}$, então ${\textstyle \lambda _{r}>0}$ quando ${\textstyle \lambda _{i}=0}$. Então o próximo passo é identificar segundo pronto crítico ${\textstyle a_{c2}}$.

Ele ocorre quando ${\textstyle \lambda _{r}=0}$ e ${\textstyle a\neq 0}$ e ${\textstyle \lambda _{i}\neq 0}$. Então substituindo:

$${\begin{aligned}\lambda _{r}'&=\alpha 'e^{-\lambda '_{r}}\cos \lambda _{i}'=0\end{aligned}}$$

Logo

$$\lambda _{i}'=\left(\pm {\frac {\pi }{2}}+n\pi \right),n\in \mathbb {Z}$$

E substituindo:

$${\begin{aligned}\lambda _{i}'&=-\alpha 'e^{-\lambda '_{r}}\sin \lambda _{i}'\\\left(\pm {\frac {\pi }{2}}+n\pi \right)&=-\alpha '\sin \left(\pm {\frac {\pi }{2}}+n\pi \right)\end{aligned}}$$

Usando a propriedade ${\textstyle \sin \left(a+b\right)=\sin a\cos b+\sin b\cos a}$ então:

$${\begin{aligned}\sin \left(\pm {\frac {\pi }{2}}+n\pi \right)&=\sin \left(\pm {\frac {\pi }{2}}\right)\cos \left(n\pi \right)+\sin \left(n\pi \right)\cos \left(\pm {\frac {\pi }{2}}\right)\\&=\pm \sin \left({\frac {\pi }{2}}\right)\cos \left(n\pi \right)\\&\pm \left(-1\right)^{n}\end{aligned}}$$

Então:

$${\begin{aligned}\left(\pm {\frac {\pi }{2}}+n\pi \right)&=\mp \left(-1\right)^{n}\alpha '\\\alpha '=&\left(-1\right)^{n}\left(\mp n\pi -{\frac {\pi }{2}}\right)\end{aligned}}$$

Então estes são os valores de ${\textstyle \alpha }$ em que temos ${\textstyle \lambda _{r}=0}$. Novamente pode ser visualizado via Geogebra:

((-1)^n (-n π - π / 2),0)
((-1)^n (+n π - π / 2),0)

Para ${\textstyle n=0}$, obtém-se então o ponto crítico desejado:

$$\alpha _{c2}=-{\frac {\pi }{2}}$$

O primeiro ponto no eixo negativo de ${\textstyle \alpha }$ em que tem-se ${\textstyle \lambda _{r}}$. Logo, o ponto de equilíbrio é estável se ${\textstyle \alpha \in \left(-{\frac {\pi }{2}},0\right)}$, se não, é instável. Pode-se observador que os resultados obtidos para o caso em que os autovalores eram apenas reais está contido neste resultado.

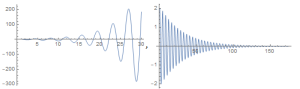
A esquerda a solução para ${\textstyle \alpha =-2<\alpha _{c2}}$ e a direita para ${\textstyle \alpha _{c2}<\alpha =-2<\alpha _{c}<0}$, considerando como condição inicial ${\textstyle y_{0}=2}$.

Antes de concluir, pode-se prestar uma atenção especial para o ponto em que as soluções complexas encontram a solução real, este é exatamente o primeiro ponto crítico. Lembrando que o primeiro ponto crítico era ${\textstyle \left(a_{c},\lambda \right)=\left({\frac {1}{e}},-1\right)}$, este resultado concorda com a equação obtida para $\lambda _{i}=0$:

$$\alpha =\lambda _{r}e^{\lambda _{r}}=-e^{-1}$$

E também no limite das equações paramétricas:

$${\begin{aligned}\lim _{\lambda _{i}\rightarrow 0}\lambda _{r}&=-\lim _{\lambda _{i}\rightarrow 0}\cot \left(\lambda _{i}\right)\lambda _{i}=-1\\\lim _{\lambda _{i}\rightarrow 0}\alpha &=\lim _{\lambda _{i}\rightarrow 0}-{\frac {\lambda _{i}}{\exp \left(\lambda _{i}\cot \left(\lambda _{i}\right)\right)\sin \lambda _{i}}}=-{\frac {1}{e}}\end{aligned}}$$

No Mathematica:

{Limit[-Cot[x]*x, x -> 0], Limit[-x/(Exp[x*Cot[x]]*Sin[x]), x -> 0]}

Principais materiais utilizados

1. Delay-Differential Equations (Richard Bertram, Universidade Estadual da Flórida)
2. Homogeneous Differential Equations (Paul Dawkins, Universidade de Lamar)

Anterior: Métodos de Lyapunov | Índice: Ecologia | Próximo: Sistemas de equações diferenciais com atrasos fixos - SIRS