Modelo de Levins aprimorado para 2 espécies
Anterior: Modelo de Lotka-Volterra amortecido | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies II
Comparação com outros modelos
Para duas espécies, vamos trabalhar com o seguinte sistema de equações:
Onde é a presa e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} o predador. Podemos comparar com outros modelos. Como um modelo inspirado no modelo de Levins, podemos ver semelhanças bastante fortes desde já. Lembrando do modelo de Levins rapidamente:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dp}{dt}=c\left(h-p\right)p-ep}
O termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(1-D-x\right)} na equação da presa é a quantidade de fragmentos disponíveis para a colonização da presa, uma vez que precisamos descontar os fragmentos destruídos, além dos ocupados. Como todos parâmetros são em termos de proporções, temos probabilidade de selecionarmos um fragmento disponível para a colonização da presa. E o termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(x_{1}-yx_{1}\right)} na equação do predador tem a mesma função, porém agora precisamos lembrar que os fragmentos que o predador pode ocupar são os que já estão ocupados pela presa, descontando os que já possuem predador. Então considerando propriedades de conjuntos, e olhando em termos de probabilidades esta equação, temos a probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P\left(x\right)} de selecionar um fragmento ocupada pela presa, mas precisamos descontar a probabilidade de selecionar um fragmento que também já esteja ocupada por um predador Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P\left(x\cap y\right)} . A maior diferença se dá porque a presa tem um termo a mais correspondendo ao decréscimo da população devido a predação, evento não considerado no modelo de Levins, mas considerado no modelo de Lotka-Volterra.
Por isso a próxima comparação que podemos fazer é com o modelo de Lotka-Volterra amortecido:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dx}{dt} = & x\left(a-\alpha y\right)-kx^{2} \\ \frac{dy}{dt} = & y\left(-c+\gamma x\right)\\ \end{align}}
Vamos reescrever nosso sistema de equações:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dx}{dt} = & x\left(c_{1}\left(1-D\right)-\mu y\right)-c_{1}x^{2}-e_{1}x \\ \frac{dy}{dt} = & y\left(-e_{y}+c_{y}x\right)-c_{y}xy^{2}\\ \end{align}}
Olhando agora primeiro para a equação da presa, a maior diferença que encontramos, e é que temos o termo de extinção local que não é devido a predação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_1x}
, algo já familiar do modelo de Levins. E já quando olhamos para a equação do predador, temos o termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(c_{y}x\right)y^{2}}
, podemos pensar também como um termo logístico, impondo um limite na população de predadores, da mesma forma que ocorre com as presas. Porém agora o termo logístico não é uma constante, mas depende também da população de presas.
Análises dos pontos de equilíbrio
Sendo todos o parâmetros como variáveis
Vamos tentar fazer análises parecidas agora. Primeiro buscar os pontos de equilíbrio pro sistema:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{cc} x\left[\left(c_{1}\left(1-D\right)-\mu y\right)-c_{1}x-e_{1}\right] & =0\\ y\left[\left(-e_{y}+c_{y}x\right)-c_{y}xy\right] & =0 \end{array}}
Temos então 4 pontos de equilíbrio:
- Primeiro: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)\rightarrow} extinção de ambas as espécies
- Segundo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\left(1-D\right)-\frac{e_{1}}{c_{1}},0\right)\rightarrow} extinção do predador
Os pontos de equilíbrio com ambas as espécies são extremamente mais complicados. Para o terceiro ponto temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{cc} x= & -\frac{\sqrt{c_{y}^{2}\mu^{2}+\left(4c_{1}c_{y}e_{y}+2c_{y}^{2}e_{1}+\left(2D-2\right)c_{1}c_{y}^{2}\right)\mu+c_{y}^{2}e_{1}^{2}+\left(2D-2\right)c_{1}c_{y}^{2}e_{1}+\left(D^{2}-2D+1\right)c_{1}^{2}c_{y}^{2}}+c_{y}\mu+c_{y}e_{1}+\left(D-1\right)c_{1}c_{y}}{2c_{1}c_{y}}\\ y= & \frac{\sqrt{c_{y}^{2}\mu^{2}+\left(4c_{1}c_{y}e_{y}+2c_{y}^{2}e_{1}+\left(2D-2\right)c_{1}c_{y}^{2}\right)\mu+c_{y}^{2}e_{1}^{2}+\left(2D-2\right)c_{1}c_{y}^{2}e_{1}+\left(D^{2}-2D+1\right)c_{1}^{2}c_{y}^{2}}+c_{y}\mu-c_{y}e_{1}+\left(1-D\right)c_{1}c_{y}}{2c_{y}\mu} \end{array}}
E o quarto e último ponto:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{cc} x= & \frac{\sqrt{c_{y}^{2}\mu^{2}+\left(4c_{1}c_{y}e_{y}+2c_{y}^{2}e_{1}+\left(2D-2\right)c_{1}c_{y}^{2}\right)\mu+c_{y}^{2}e_{1}^{2}+\left(2D-2\right)c_{1}c_{y}^{2}e_{1}+\left(D^{2}-2D+1\right)c_{1}^{2}c_{y}^{2}}-c_{y}\mu-c_{y}e_{1}-\left(D-1\right)c_{1}c_{y}}{2c_{1}c_{y}}\\ y=- & \frac{\sqrt{c_{y}^{2}\mu^{2}+\left(4c_{1}c_{y}e_{y}+2c_{y}^{2}e_{1}+\left(2D-2\right)c_{1}c_{y}^{2}\right)\mu+c_{y}^{2}e_{1}^{2}+\left(2D-2\right)c_{1}c_{y}^{2}e_{1}+\left(D^{2}-2D+1\right)c_{1}^{2}c_{y}^{2}}-c_{y}\mu+c_{y}e_{1}-\left(1-D\right)c_{1}c_{y}}{2c_{y}\mu} \end{array}} Estes últimos pontos (com o equilíbrio entre as espécies) são complicados demais para nos referirmos explicitamente daqui em diante quando necessário utilizamos alguma notação como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{j},y_{j}\right)} para denotar o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle j-\acute{e}simo} ponto de equilíbrio, sem escrevê-lo por inteiro. Vamos linearizar e analisar a estabilidade em torno dos pontos de equilíbrio. Para o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)} é muito simples:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=x\left(c_{1}\left(1-D\right)-\mu y\right)-c_{1}x^{2}-e_{1}x} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}=y\left(-e_{y}+c_{y}x\right)-c_{y}xy^{2}}
Separando os termos lineares dos não lineares:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=\left[x\left(c_{1}\left(1-D\right)-e_{1}\right)\right]-\left[\mu yx+c_{1}x^{2}\right]} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}=-\left[ye_{y}\right]+\left[c_{y}xy-c_{y}xy^{2}\right]}
Calculando então os limites:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\mu yx+c_{1}x^{2}}{x\left(c_{1}\left(1-D\right)-e_{1}\right)}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\mu y+c_{1}x}{c_{1}\left(1-D\right)-e_{1}}=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{c_{y}xy-c_{y}xy^{2}}{ye_{y}}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{c_{y}x-c_{y}xy}{e_{y}}=0}
Desprezando os termos não lineares:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} c_{1}\left(1-D\right)-e_{1} & 0\\ 0 & -e_{y} \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)}
Logo um dos autovalores é real, sempre negativo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(-e_{y}\right)} e o segundo é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(c_{1}\left(1-D\right)-e_{1}\right)} . Basicamente se o termo de colonização do guanaco for maior que o da extinção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(c_{1}\left(1-D\right)>e_{1}\right)} , temos dois autovalores de sinais opostos, ou seja, um ponto de instabilidade. Aumentando a taxa de extinção do guanaco (ou a destruição do habitat) passamos a ter Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}\left(1-D\right)<e_{1}} , e a extinção de ambas as espécies. Aqui podemos notar uma diferença dos modelos de Lotka-Volterra: a extinção de ambas as espécies pode ser um ponto de equilíbrio estável. Ou seja nos modelos anteriores o sistema nunca iria para o equilíbrio com extinção total, agora há essa possibilidade dependendo do nível de destruição do sistema.
Para o segundo ponto de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{2},y_{2}\right)=\left(x_{2},0\right)} precisamos fazer a translação: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=x-x_{2}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v=y} .
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left[\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)u+\left(-\mu x_{2}\right)v+\left(-c_{1}x_{2}^{2}-e_{1}x_{2}+\left(1-D\right)x_{2}c_{1}\right)\right]+\left[-\mu uv-c_{1}u^{2}\right]} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\left[\left({\it c_{y}}x_{2}-{\it e_{y}}\right)v\right]+\left[-{\it c_{y}}v^{2}x_{2}-{\it c_{y}}uv^{2}+{\it c_{y}}uv\right]}
Podemos ver facilmente que é semi linear para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{u}} uma vez que ao fazermos os:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}\frac{\text{parte não-linear}}{\text{parte linear}}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{-\mu uv-c_{1}u^{2}}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)u+\left(-\mu x_{2}\right)v}}
Fazendo a substituição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r^{2}=x^{2}+y^{2}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x,y\right)=\left(r\cos\theta,r\sin\theta\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r^{2}\left(-\mu\cos\theta\sin\theta-c_{1}\cos\theta^{2}\right)}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)r\cos\theta+\left(-\mu x_{2}\right)r\sin\theta}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r\left(-\mu\cos\theta\sin\theta-c_{1}\cos\theta^{2}\right)}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)\cos\theta+\left(-\mu x_{2}\right)\sin\theta}=0}
É interessante notar que a parte constante vai zerar. E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{v}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\left[-{\it c_{y}}v^{2}x_{2}-{\it c_{y}}uv^{2}+{\it c_{y}}uv\right]}{\left[\left({\it c_{y}}x_{2}-{\it e_{y}}\right)v\right]}=\frac{\left[-{\it c_{y}}vx_{2}-{\it c_{y}}uv+{\it c_{y}}u\right]}{\left[\left({\it c_{y}}x_{2}-{\it e_{y}}\right)\right]}=0}
Analisando o comportamento linear então na proximidade do ponto de equilíbrio:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1} & -\mu x_{2}\\ 0 & {\it c_{y}}x_{2}-{\it e_{y}} \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} E os autovalores são então:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1}=\left(1-D-\frac{e_{1}}{c_{1}}\right)c_{y}-e_{y}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{2}=e_{1}-\left(1-D\right)c_{1}}
Podemos ver que o segundo autovalor tem uma relação entre a extinção e a colonização dos guanacos, se tivermos um valor suficientemente alto de colonização então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(1-D\right)c_{1}>e_{1}\rightarrow\lambda_{2}<0} . E no primeiro autovalor temos uma relação entre a colonização e morte de predadores, se a morte de predadores for suficientemente alta Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}>\left(1-D-\frac{e_{1}}{c_{1}}\right)c_{y}} então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1}<0} . Com as duas condições satisfeitas, temos um ponto de equilíbrio onde os predadores são extintos, e só restam presas.
E por fim, temos dois pontos que suportam a coexistência entre duas espécies. Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{3},y_{3}\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\begin{array}{c} \left[\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)u+\left(-\mu x_{3}\right)v+\left(-\mu x_{3}y_{3}-c_{1}x_{3}^{2}-e_{1}x_{3}+\left(1-D\right)c_{1}x_{3}\right)\right]+\\ \left[-\mu uv-c_{1}u^{2}\right] \end{array}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\begin{array}{c} \left[\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)u+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)v+\left(c_{y}x_{3}y_{3}-y_{3}^{2}c_{y}x_{3}-e_{y}y_{3}\right)\right]+\\ \left[-2c_{y}uvy_{3}-c_{y}v^{2}x_{3}-c_{y}uv^{2}+c_{y}uv\right] \end{array}} Calculando os limites para verificar o comportamento semi linear:Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}\frac{\text{parte não-linear}}{\text{parte linear}}}
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{u}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{-\mu uv-c_{1}u^{2}}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)u+\left(-\mu x_{3}\right)v}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r^{2}\left(-\mu\cos\theta\sin\theta-c_{1}\cos^{2}\theta\right)}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)r\cos\theta+\left(-\mu x_{3}\right)r\sin\theta}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r\left(-\mu\cos\theta\sin\theta-c_{1}\cos^{2}\theta\right)}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)\cos\theta+\left(-\mu x_{3}\right)\sin\theta}=0}
E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{v}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{-2c_{y}uvy_{3}-c_{y}v^{2}x_{3}-c_{y}uv^{2}+c_{y}uv}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)u+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)v}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r^{2}\left(-2c_{y}\cos\theta\sin\theta y_{3}-c_{y}\sin^{2}\theta x_{3}-c_{y}\cos\theta\sin^{2}\theta+c_{y}\cos\theta\sin\theta\right)}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)r\cos\theta+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)r\sin\theta}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r\left(-2c_{y}\cos\theta\sin\theta y_{3}-c_{y}\sin^{2}\theta x_{3}-c_{y}\cos\theta\sin^{2}\theta+c_{y}\cos\theta\sin\theta\right)}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)\cos\theta+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)\sin\theta}=0}
Montando a matriz linearizada então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} \left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3} & -\mu x_{3}\\ c_{y}y_{3}-y_{3}^{2}c_{y} & c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3} \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Infelizmente o autovalor é extremamente complexo se vamos considerar todos os parâmetros como variáveis. A partir de agora, vamos trabalhar atribuindo valores numéricos aos parâmetros, exceto o fato de destruição do habitat, que é um parâmetro que estamos interessado em analisar como afeta a dinâmica.
Caso particular 1: Utilizando os parâmetros do artigo
Utilizando o seguinte conjunto de parâmetros
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}=0.1}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{1}=0.025}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}=0.015}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \mu=0.3}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{y}=0.015}
Temos os seguintes pontos de equilíbrio com os respectivos autovalores:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1,k}\in\left\{ -\frac{3}{200},\frac{\left(0.75-D\right)}{10}\right\}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{2},y_{2}\right)=\left(0.75-D,0\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{2,k}\in\left\{ -\frac{12D+3}{800},\frac{\left(D-0.75\right)}{10}\right\}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{3},y_{3}\right)=\left(\frac{-4D-9-\sqrt{16D^{2}+72D+273}}{8},\frac{-4D+\left(\sqrt{16D^{2}+72D+273}+15\right)}{24}\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{3,1}=\frac{23\sqrt{16D^{2}+72D+273}+92D+231-\sqrt{2}\sqrt{\left(1156D+1233\right)\sqrt{16D^{2}+72D+273}+4624D^{2}+23016D+33369}}{3200}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{3,2}=\frac{23\sqrt{16D^{2}+72D+273}+92D+231+\sqrt{2}\sqrt{\left(1156D+1233\right)\sqrt{16D^{2}+72D+273}+4624D^{2}+23016D+33369}}{3200}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{4},y_{4}\right)=\left(\frac{-4D-9+\sqrt{16D^{2}+72D+273}9}{8},\frac{-4D-\left(\sqrt{16D^{2}+72D+273}+15\right)}{24}\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{4,1}=\frac{-23\sqrt{16D^{2}+72D+273}+92D+231-\sqrt{2}\sqrt{\left(-1156D-1233\right)\sqrt{16D^{2}+72D+273}+4624D^{2}+23016D+33369}}{3200}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{4,2}=\frac{-23\sqrt{16D^{2}+72D+273}+92D+231+\sqrt{2}\sqrt{\left(-1156D-1233\right)\sqrt{16D^{2}+72D+273}+4624D^{2}+23016D+33369}}{3200}}
Para o primeiro ponto ele está fixo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} e podemos perceber que um autovalor é negativo e o outro depende se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} é maior ou menor que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.75} . Para fatores de destruição maior, ambos autovalores são negativos e temos um ponto de equilíbrio estável com a extinção de ambas espécies, para fatores de destruição menor, temo um ponto instável.
Para o segundo ponto de equilíbrio, temos novamente uma dependência da relação entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.75} . O próprio pronto vai se aproximando a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} conforme Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} cresce. Além disso para valores em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D<0.75} temos um ponto de equilíbrio estável e para acima deste valores se torna instável. Lembrando que para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D>0.75} o ponto já passa a ter uma população negativa de pumas, o que não faz sentido ecologicamente, enquanto o primeiro ponto de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} se torna estável. Então “recuperamos”o resultado do primeiro ponto de equilíbrio.
Os próximos como pode-se imaginar são mais complicados de se analisar, por isso vamos utilizar gráficos para trabalhar.
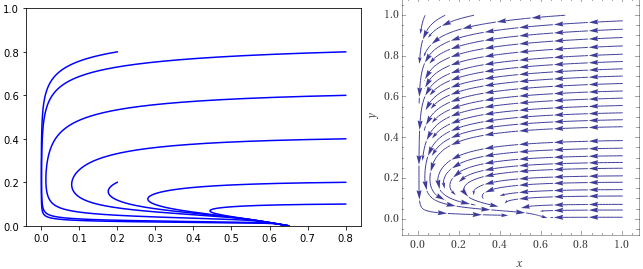
Os dois pontos de equilíbrio tem uma população negativa, e um auto valor positivo, portanto são pontos que não fazem sentido ecologicamente e matematicamente são pontos de equilíbrio instável. Desta forma, o sistema sempre evolui para a extinção de ambas as espécies, como podemos ver no espaço de fazes. Seja calculando a evolução do sistema para diferentes condições inciais, ou fazendo o rascunho do diagrama de fase.
Caso particular 2: Fatores de colonização aumentados
Análogo ao problema do modelo de Levins, este modelo ainda carrega a deficiência de não considerar a configuração espacial. Vamos analisar outro cenário que damos multiplicamos por 4 as taxas de colonização, com o objetivo de analisarmos um cenário em que há coexistência entre presas epredadores.
Repetindo os cálculos temos que o primeiro ponto de equilíbrio é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} , com os autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(-\frac{3}{200},\frac{16}{40}\left(0.9375-D\right)\right)} , então agora para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D<0.9375} , este é um ponto de equilíbrio instável. O segundo ponto de equilíbrio é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(D-0.9375,0\right)} com os autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{48}{800}\left(0.6875-D\right),\frac{16}{40}\left(D-0.9375\right)\right)} , então para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D<0.6875} temos temos o par de sinai dos autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(+,-\right)} , para valores maiores que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D>0.9375} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(-,+\right)} e para valores intermediários Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.6875<D<0.9375} temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(-,-\right)} . O que isso significa?
Bom, para valores maiores que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.9375}
então temos um ponto de equilíbrio instável,e nessa situação o ponto estável é em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)}
ou seja, esperamos o a extinção de de ambas as espécies. Para valores entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.6875<D<0.9375}
temos um ponto de equilíbrio estável, nessa situação, apenas a presa sobrevive. E para valores menores, temos um ponto de equilíbrio instável. E esperamos que os próximos dois pontos de equilíbrio nos ajude a responder o que acontece. Semelhante à discussão anterior, os próximos dois pontos são melhores analisados através de gráficos.
Para o terceiro ponto de equilíbrio, sempre temos população de presas negativas, o que não fez sentido ecologicamente. Esse resultadoé coerente matematicamente pois a parte real dos autovalores são sempre positivos, então é um ponto instável. E por fim, o mais interessante é o quarto ponto de equilíbrio. Para este ponto, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D=0.6875} é exatamente o valor no qual deixa de ser um ponto que ecologicamente faz sentido e também deixa de ser um ponto de equilíbrio estável, e para valores menores que este, tempos um ponto de equilíbrio estável. Então resumidamente, temos
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D<0.6875} : Coexistência de ambas espécies;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.6875<D<0.9375} : Sobrevivência da presa;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.9375<D} : Extinção de todas as espécies.
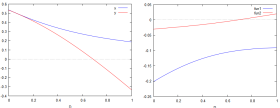
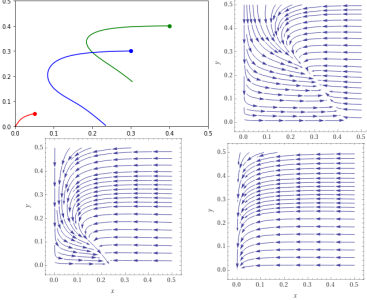
Plotando então a evolução e diagramas de fases para 3 valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.5,0.7,0.96} ), temos:
Códigos
Script para o WxMaxima utilizado para efetuar os cálculos simbólicos necessários para analisar os pontos de equilíbrio considerando todos parâmetros como variáveis:
Cálculos simbólico do modelo de Levins aprimorado para 2 espécies considerando todos parâmetros como variáveis Jhordan Silveira de Borba sbjhordan@gmail.com --> ratprint: false$ Declaração do sistema de equações: --> dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x); dy:(y*(-e_y+c_y*x)-c_y*x*y^2); Soluções e verificação das soluções --> sol:(algsys([dx, dy], [x,y])); N:1;radcan(dx),sol[N][1],sol[N][2]; radcan(dy),sol[N][1],sol[N][2]; Segundo ponto: - Deslocamento - Verificação que a solução linear tem o mesmo ponto de equilíbrio e autovalor - Aqui se a partir de A2 tivermos x_2=x, então x é a posição do ponto de equilíbrio, e não uma variável. --> radcan(dx),x=u+x_2,y=v;radcan(dy),x=u+x_2,y=v; --> B:matrix([u],[v]); A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x; C2:matrix([-c_1*x_2^2-e_1*x_2+(1-D)*x_2*c_1],[0]),x_2=x; radcan(A2.B),u=0,v=0,sol[2][1]; radcan(C2),u=0,v=0,sol[2][1]; radcan(eigenvalues(A2)),sol[2][1]; Terceiro e quarto ponto ponto: - Deslocamento - Verificação que a solução linear tem o mesmo ponto de equilíbrio e autovalor - Aqui se a partir de A3 tivermos x_3=x e y_3=y, então x e y são a posição do ponto de equilíbrio, e não uma variável. --> radcan(dx),x=u+x_3,y=v+y_3;radcan(dy),x=u+x_3,y=v+y_3; --> A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y; C3:matrix([-mu*x_3*y_3-c_1*x_3^2-e_1*x_3+(1-D)*c_1*x_3],[c_y*x_3*y_3-y_3^2*c_y*x_3-e_y*y_3]),x_3=x,y_3=y; radcan(A3.B),u=0,v=0,sol[3][1],sol[3][2]; radcan(C3),u=0,v=0,sol[3][1],sol[3][2]; radcan(C3),u=0,v=0,sol[4][1],sol[4][2]; radcan(eigenvalues(A3)),sol[3][1],sol[3][2];
Script para calcularmos os pontos de equilíbrio e autovalores do sistema tendo a fração de destruição do sistema como única variável:
Análise utilizando como variável apenas D Jhordan Silveira de Borba sbjhordan@gmail.com - Repetimos todos os cálculos substituindo as variáveis pelos valores - Plotamos os gráficos - Obs.: Para obtermos a parte real usamos realpart(%) e a imaginária imagpart(%) --> c_1:0.1;e_1:0.025;e_y:0.015;mu:0.3;c_y:0.015; dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x); dy:(y*(-e_y+c_y*x)-c_y*x*y^2); sol:(algsys([dx, dy], [x,y])); B:matrix([u],[v]); A1:matrix([c_1*(1-D)-e_1,0],[0,-e_y]); A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x; A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y; l1:radcan(eigenvalues(A1)); l2:radcan(eigenvalues(A2)),sol[2][1]; l3:radcan(eigenvalues(A3)),sol[3][1],sol[3][2]; l4:radcan(eigenvalues(A3)),sol[4][1],sol[4][2]; --> X:x,sol[3][1];Y:y,sol[3][2]; wxplot2d([X,Y], [D,0,1],[legend,"x","y"]); wxplot2d([l3[1][1],l3[1][2]], [D,0,1]); X:x,sol[4][1];Y:y,sol[4][2]; wxplot2d([X,Y], [D,0,1],[legend,"x","y"]); wxplot2d([l4[1][1],l4[1][2]], [D,0,1]);
Script para calcularmos os vetores em torno de cada ponto de equilíbrio, para que possamos fazer um rascunho do plano de fase.
Calculo de vetores para o rascunho do plano de fase com D=0.1: Jhordan Silveira de Borba --> D:0.1;c_1:0.1;e_1:0.025;e_y:0.015;mu:0.3;c_y:0.015; dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x); dy:(y*(-e_y+c_y*x)-c_y*x*y^2); sol:(algsys([dx, dy], [x,y])),numer; B:matrix([u],[v]); A1:matrix([c_1*(1-D)-e_1,0],[0,-e_y]); A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x; C2:matrix([-c_1*x_2^2-e_1*x_2+(1-D)*x_2*c_1],[0]),x_2=x; A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y; C3:matrix([-mu*x_3*y_3-c_1*x_3^2-e_1*x_3+(1-D)*c_1*x_3],[c_y*x_3*y_3-y_3^2*c_y*x_3-e_y*y_3]),x_3=x,y_3=y; l1:radcan(eigenvalues(A1)),numer; l2:radcan(eigenvalues(A2)),sol[2][1],numer; l3:radcan(eigenvalues(A3)),sol[3][1],sol[3][2],numer; l4:radcan(eigenvalues(A3)),sol[4][1],sol[4][2],numer; --> radcan((A1.B)); radcan((A2.B)),sol[2][1]; radcan((A3.B)),sol[3][1],sol[3][2]; radcan((A3.B)),sol[4][1],sol[4][2];
Script em Python para plotar o rascunho do diagrama de fases, pode ser editado para visualizarmos só a vizinhança de cada ponto.
# -*- coding: utf-8 -*-
# Modelo aprimorado de Levins para 2 espécies: Diagrama de fases
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
import matplotlib.pyplot as plt
import numpy as np
def phase_lot():
p1=[0.,0.] # Ponto de equilíbrio 1
p2=[0.65,0.] # Ponto de equilíbrio 2
p3=[-3.27,1.31] # Ponto de equilíbrio 3
p4=[0.92,-0.09] # Ponto de equilíbrio 4
X = np.arange(0,1, 0.1/2) # Eixo X
Y = np.arange(0,1, 0.1/2) # Eixo Y
U,V=np.meshgrid(X,Y)
c=0
for x in X:
l=0
for y in Y:
#Distâncias
d=[]
d.append(np.sqrt((x-p1[0])*(x-p1[0])+(y-p1[1])*(y-p1[1])))
d.append(np.sqrt((x-p2[0])*(x-p2[0])+(y-p2[1])*(y-p2[1])))
d.append(np.sqrt((x-p3[0])*(x-p3[0])+(y-p3[1])*(y-p3[1])))
d.append(np.sqrt((x-p4[0])*(x-p4[0])+(y-p4[1])*(y-p4[1])))
for i in range(len(d)):
if (min(d)==d[i]):
p=i
#Calculamos o vetor baseado no ponto mais próximo:
if(p==0):
u=x-p1[0]
v=y-p1[1]
a=(13*u)/200
b=-(3*v)/200
elif (p==1):
u=x-p2[0]
v=y-p2[1]
a=-(70*v+23*u+25)/36
b=-(21*v)/40
elif(p==2):
u=x-p3[0]
v=y-p3[1]
a=(285*v+80*u-5)/29
b=(11*v-10*u)/17
elif(p==3):
u=x-p4[0]
v=y-p4[1]
a=-(47*v+15*u+12)/17
b=(20*v-21*u-66)/18
else:
print("Algo deu errado")
m=np.sqrt(a*a+b*b) # Módulo do vetor
if(m==0):
m=1
# Normalizamos e salvamos o vetor: [dx/dt,dy/dt]=[a,b]
U[l,c]=a/m
V[l,c]=b/m
l=l+1
c=c+1
fig, ax = plt.subplots()
ax.quiver(X, Y, U, V)
plt.plot(p0[0],p0[1],'ko') #Plotamos o primeiro ponto de equilíbrio
plt.plot(p1[0],p1[1],'ko') #Plotamos o segundo ponto de equilíbrio
plt.plot(p3[0],p2[1],'ko') #Plotamos o terceiro ponto de equilíbrio
plt.plot(p4[0],p3[1],'ko') #Plotamos o quarto ponto de equilíbrio
plt.show()
Script em Python para analisar a evolução do sistema no espaço de fases, utilizando o método de Euler:
# -*- coding: utf-8 -*-
# Modelo aprimorado de Levins para 2 espécies: evolução do sistema no espaçode estados
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
def phase2():
#Parâmetros
c1=0.1 # Fator de colonização do guanaco
cy=0.015 # Fator de colonização do puma
e1=0.025 # Fator de extinção local do guanaco
ey=0.015 # Fator de extinção local do puma
u1=0.3 # Fator de predação do guanaco
N=int(200000) # Duração da simulação
d=0.01 # Tamanho do passo
D=0.5 # Destruição do habitat
p1=[0.,0.] # Ponto de equilíbrio 1
p2=[0.65,0.] # Ponto de equilíbrio 2
p3=[-3.26,1.30] # Ponto de equilíbrio 3
p4=[0.92,-0.09] # Ponto de equilíbrio 4
#Valores iniciais:
init=[(0.4,0.4),(0.3,0.3),(0.05,0.05)]
c=0
for it in init:
x=[]
y=[]
x.append(it[0])
y.append(it[1])
for i in range(N-1):
x.append(x[i]+d*(c1*x[i]*(1-D-x[i])-e1*x[i]-u1*x[i]*y[i]))
y.append(y[i]+d*(cy*y[i]*(x[i]-y[i]*(x[i]))-ey*y[i]))
if(c==0):
plt.plot(x,y,'g-')
plt.plot(it[0],it[1],'go')
D=0.7
elif (c==1):
plt.plot(x,y,'b-')
plt.plot(it[0],it[1],'bo')
D=0.95
else:
plt.plot(x,y,'r-')
plt.plot(it[0],it[1],'ro')
c=c+1
plt.plot(p1[0],p1[1],'ko')
plt.plot(p2[0],p2[1],'ko')
plt.plot(p3[0],p3[1],'ko')
plt.plot(p4[0],p4[1],'ko')
plt.xlim(0,0.5)
plt.ylim(0,0.5)
plt.show()
Principal material utilizado
- Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances (Fabiana Laguna e outros, Ecological Modelling)
Anterior: Modelo de Lotka-Volterra amortecido | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies II