Modelo de Lotka-Volterra amortecido

Anterior: Modelo de Lotka-Volterra | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies I

Uma versão do modelo de Lotka-Volterra aprimorada inclui um termo de saturação na população de presas, isto é, um termo logístico (que inibe o aumento exponencial) visando representar a finitude dos recursos disponíveis para uma espécie. Este modelo é chamado de modelo de Lotka-Volterra amortecido.

• ${\textstyle {\frac {dx}{dt}}=x\left(a-\alpha y\right)-kx^{2}}$
• ${\textstyle {\frac {dy}{dt}}=y\left(-c+\gamma x\right)}$

Onde ${\textstyle k}$ é uma constante positiva. Agora temos três pontos de equilíbrio, novamente temos ${\textstyle \left(0,0\right)}$. Mas temos outro ponto quando apenas ${\textstyle y=0}$:

$$a-\alpha y-kx=a-kx=0\rightarrow x={\frac {a}{k}}$$

Então ${\textstyle \left({\frac {a}{k}},0\right)}$ ou seja um ponto de equilíbrio com apenas a sobrevivência da presa. E ainda temos também um ponto de coexistência entre ambas as espécies:

$$a-\alpha y-kx=0$$

$$-c+\gamma x=0$$

Isolando então ${\textstyle x}$ na segunda equação ${\textstyle x={\frac {c}{\gamma }}}$ e substituindo na primeira:

$$a-\alpha y-k{\frac {c}{\gamma }}=0$$

Então:

$$y={\frac {a}{\alpha }}-{\frac {kc}{\alpha \gamma }}={\frac {\gamma a-kc}{\alpha \gamma }}$$

Então nosso outro ponto de equilíbrio é dado por${\textstyle \left({\frac {c}{\gamma }},{\frac {\gamma a-kc}{\alpha \gamma }}\right)}$. Infelizmente as equações não são separáveis como no caso anterior, portanto vamos analisar se a equação é semi-linear nas proximidades dos pontos de equilíbrio. Para ${\textstyle \left(0,0\right)}$:

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\alpha xy-kx^{2}}{xa}}=\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\alpha y-kx}{a}}=0$$

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\gamma xy}{cy}}=\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\gamma }{c}}x=0$$

Para ${\textstyle \left({\frac {a}{k}},0\right)}$ e fazendo a mudança de variáveis ${\textstyle u=x-{\frac {a}{k}}}$, e ${\textstyle v=y}$, temos:

$${\frac {du}{dt}}=\left(\left(u+{\frac {a}{k}}\right)a-k\left(u+{\frac {a}{k}}\right)^{2}\right)-\left(\alpha \left(u+{\frac {a}{k}}\right)v\right)$$

$${\frac {du}{dt}}=\left(ua+{\frac {a^{2}}{k}}-\left(u^{2}k+{\frac {a^{2}}{k}}+2ua\right)\right)-\left(\alpha uv+{\frac {\alpha a}{k}}v\right)$$

$${\frac {du}{dt}}=-\left(ua+{\frac {\alpha a}{k}}v\right)-\left(\alpha uv+u^{2}k\right)$$

E:

$${\frac {dv}{dt}}=\left(-vc\right)+\left(\gamma v\left(u+{\frac {a}{k}}\right)\right)=v\left(\gamma {\frac {a}{k}}-c\right)+\left(\gamma vu\right)$$

Então:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}\left({\frac {\alpha uv+u^{2}k}{ua+{\frac {\alpha a}{k}}v}}\right)=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}\left({\frac {\alpha uv+u^{2}k}{u\left(a+{\frac {\alpha a}{k}}{\frac {v}{u}}\right)}}\right)=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}\left({\frac {\alpha v+uk}{\left(a+{\frac {\alpha a}{k}}{\frac {v}{u}}\right)}}\right)$$

Podemos fazer uma substituição de variável novamente usando coordenadas polares ${\textstyle r^{2}=u^{2}+v^{2}}$ e ${\textstyle u=r\cos \theta }$, ${\textstyle v=r\sin \theta }$, então:

$$\lim _{r\rightarrow 0}\left({\frac {\alpha r\sin \theta +kr\cos \theta }{\left(a+{\frac {\alpha a}{k}}{\frac {r\sin \theta }{r\cos \theta }}\right)}}\right)=\lim _{r\rightarrow 0}\left({\frac {\alpha kr\sin \theta +k^{2}r\cos \theta }{\left(ka+\alpha a\tan \theta \right)}}\right)=0$$

E o limite:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma vu}{v\left(\gamma {\frac {a}{k}}-c\right)}}=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma u}{\left(\gamma {\frac {a}{k}}-c\right)}}=0$$

E por fim, vamos estudar os pontos de estabilidade em torno de ${\textstyle \left({\frac {c}{\gamma }},{\frac {\gamma a-kc}{\alpha \gamma }}\right)}$, tendo agora ${\textstyle u=x-{\frac {c}{\gamma }}}$ e ${\textstyle v={\frac {\gamma a-kc}{\alpha \gamma }}-y}$, então, manipulando novamente, primeiro trabalhando com ${\dot {x}}$:

$${\frac {dx}{dt}}=\left(xa-kx^{2}\right)-\left(\alpha xy\right)$$

$${\frac {du}{dt}}=\left(\left({\frac {c}{\gamma }}+u\right)a-k\left({\frac {c}{\gamma }}+u\right)^{2}\right)-\left(\alpha \left({\frac {c}{\gamma }}+u\right)\left(v+{\frac {\gamma a-kc}{\alpha \gamma }}\right)\right)$$

$${\frac {du}{dt}}=\left({\frac {ca}{\gamma }}+au-{\frac {kc^{2}}{\gamma ^{2}}}-ku^{2}-{\frac {2ck}{\gamma }}u\right)-\left({\frac {c\alpha }{\gamma }}v+{\frac {\gamma ac-kc^{2}}{\gamma ^{2}}}+\alpha uv+\left[{\frac {\gamma a-kc}{\gamma }}\right]u\right)$$

$${\frac {du}{dt}}=\left(\left({\frac {ca}{\gamma }}-{\frac {kc^{2}}{\gamma ^{2}}}-{\frac {\gamma ac-kc^{2}}{\gamma ^{2}}}\right)+\left(a-{\frac {2ck}{\gamma }}-\left[{\frac {\gamma a-kc}{\gamma }}\right]-ku\right)u-{\frac {c\alpha }{\gamma }}v\right)-\left(\alpha uv\right)$$

$${\frac {du}{dt}}=\left(\left(-{\frac {kc}{\gamma }}-ku\right)u-{\frac {c\alpha }{\gamma }}v\right)-\left(\alpha uv\right)$$

$${\frac {du}{dt}}=-\left({\frac {kc}{\gamma }}u+{\frac {c\alpha }{\gamma }}v\right)-\left(\alpha uv+ku^{2}\right)$$

E com ${\dot {y}}$:

$${\frac {dy}{dt}}=\left(-yc\right)+\left(\gamma yx\right)$$

$${\frac {dv}{dt}}=\left(-\left(v+{\frac {\gamma a-kc}{\alpha \gamma }}\right)c\right)+\left(\gamma \left(v+{\frac {\gamma a-kc}{\alpha \gamma }}\right)\left({\frac {c}{\gamma }}+u\right)\right)$$

$${\frac {dv}{dt}}=\left(-vc-{\frac {ac}{\alpha }}+{\frac {kc^{2}}{\alpha \gamma }}\right)+\left(vc+{\frac {\gamma ac-kc^{2}}{\alpha \gamma }}+\gamma uv+\left[{\frac {\gamma a-kc}{\alpha }}\right]u\right)$$

$${\frac {dv}{dt}}=\gamma uv+\left[{\frac {\gamma a-kc}{\alpha }}\right]u$$

Calculando então os limites, relacionado a $u$:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}\left({\frac {\alpha uv+ku^{2}}{{\frac {kc}{\gamma }}u+{\frac {c\alpha }{\gamma }}v}}\right)=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}\left({\frac {\alpha uv+ku^{2}}{u\left({\frac {kc}{\gamma }}+{\frac {c\alpha }{\gamma }}{\frac {v}{u}}\right)}}\right)=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}\left({\frac {\alpha v+ku}{{\frac {kc}{\gamma }}+{\frac {c\alpha }{\gamma }}{\frac {v}{u}}}}\right)$$

E novamente fazendo a substituição ${\textstyle r^{2}=u^{2}+v^{2}}$ e ${\textstyle u=r\cos \theta }$, ${\textstyle v=r\sin \theta }$, então:

$$\lim _{r\rightarrow 0}\left({\frac {\alpha r\sin \theta +kr\cos \theta }{{\frac {kc}{\gamma }}+{\frac {c\alpha }{\gamma }}{\frac {r\sin \theta }{r\cos \theta }}}}\right)=\lim _{r\rightarrow 0}\left({\frac {r\alpha \gamma \sin \theta +rk\gamma \cos \theta }{kc+c\alpha \tan \theta }}\right)=0$$

E a $v$:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma uv}{\left[{\frac {\gamma a-kc}{\alpha }}\right]u}}=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma v}{\left[{\frac {\gamma a-kc}{\alpha }}\right]}}=0$$

Então os três pontos são semi-lineares. A partir disto, podemos analisar os tipos de estabilidades. Para ${\textstyle \left(0,0\right)}$:

$$\left({\begin{array}{c}{\dot {x}}\\{\dot {y}}\end{array}}\right)=\left({\begin{array}{cc}a&0\\0&-c\end{array}}\right)\left({\begin{array}{c}x\\y\end{array}}\right)$$

Então:

$$\left(a-\lambda \right)\left(c+\lambda \right)=0$$

Novamente temos duas raízes reais de sinais opostos, então temos um ponto de sela, uma instabilidade. Para o segundo ponto:

$$\left({\begin{array}{c}{\dot {u}}\\{\dot {v}}\end{array}}\right)=\left({\begin{array}{cc}-a&-{\frac {\alpha a}{k}}\\0&\gamma {\frac {a}{k}}-c\end{array}}\right)\left({\begin{array}{c}u\\v\end{array}}\right)$$

Então:

$$\left(-a-\lambda \right)\left(\left({\frac {\gamma a}{k}}-c\right)-\lambda \right)=0$$

$$\left(a+\lambda \right)\left(\left({\frac {\gamma a}{k}}-c\right)-\lambda \right)=0$$

Temos duas raízes reais uma é negativa ${\textstyle \lambda _{1}=-a}$. Porém a classificação do ponto depende dos parâmetros escolhidos. Se ${\textstyle \left({\frac {\gamma a}{k}}-c\right)>0}$ ou seja ${\textstyle \gamma a>ck}$, temos uma instabilidade, uma sela, mas se ${\textstyle \gamma a<ck}$, então temos um nó hiperbólico, ou seja, estabilidade. E por último:

$$\left({\begin{array}{c}{\dot {u}}\\{\dot {v}}\end{array}}\right)=\left({\begin{array}{cc}-{\frac {kc}{\gamma }}&-{\frac {c\alpha }{\gamma }}\\{\frac {\gamma a-kc}{\alpha }}&0\end{array}}\right)\left({\begin{array}{c}u\\v\end{array}}\right)$$

Então:

$$\left({\frac {kc}{\gamma }}+\lambda \right)\lambda +{\frac {c\alpha }{\gamma }}\left({\frac {\gamma a-kc}{\alpha }}\right)=0$$

$$\gamma \lambda ^{2}+kc\lambda +c\left(\gamma a-kc\right)=0$$

Então:

$$\lambda =-\left({\frac {kc}{2\gamma }}\right)\pm {\frac {\sqrt {\left(kc\right)^{2}-4\gamma c\left(\gamma a-kc\right)}}{2\gamma }}$$

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=-\left(\frac{kc}{2\gamma}\right)\pm\frac{\sqrt{\left[\left(kc\right)^{2}+4\gamma c^{2}k\right]-4c\gamma^{2}a}}{2\gamma}}

Então o comportamento do sistema vai depender da escolha de parâmetros, porém como todas constantes são positivas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle -\left(\frac{kc}{2\gamma}\right)} vai ser sempre negativo, e a única forma de ser instável é se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(kc\right)^{2}+4\gamma c^{2}k>4c\gamma^{2}a} , para garantir que o número seja real, e ainda Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{\sqrt{\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a}}{2\gamma}>\frac{kc}{2\gamma}} para que o autovalor seja positivo. Analisando então essa última desigualdade:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sqrt{\left(kc\right)^{2}+4\gamma c^{2}kc-4c\gamma^{2}a}}{2\gamma}>\frac{kc}{2\gamma}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a}>kc}

Elevando ao quadrado:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a>\left(kc\right)^{2}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4\gamma c^{2}k-4c\gamma^{2}a>0}

Dividindo por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 4c\gamma}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ck-\gamma a>0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ck>\gamma a}

Então essa é a condição para que o autovalor seja positivo. E olhando pra primeira desigualdade:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(kc\right)^{2}+4\gamma c^{2}k>4c\gamma^{2}a} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{k^{2}c}{4\gamma}+ck>\gamma a}

Para garantir que o número seja real. Então temos duas desigualdades para satisfazer para que seja instável:

• Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ck>\gamma a}
• Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{k^{2}c}{4\gamma}+ck>\gamma a}

Como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{k^{2}c}{4\gamma}\right)} é necessariamente um termo positivo:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma a<ck<\frac{k^{2}c}{4\gamma}+ck}

Ou seja, podemos restringir a condição de instabilidade para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ck>\gamma a} pois Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ck<\frac{k^{2}c}{4\gamma}+ck} é uma desigualdade válida para qualquer escolha de parâmetros válidos. Mas lembrando que para o outro ponto é estável se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ck>\gamma a} , então sempre temos um ponto de equilíbrio estável e outro instável (além do a instabilidade na origem). Ou seja, por exemplo para valores mais baixos de de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c} (termo de crescimento dos predadores) ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k} (termo de amortecimento da presa) temos coexistência de ambas as espécies, se aumentar estes parâmetros, somente a presa sobrevive. Além disso, quando temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=0} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\pm\frac{\sqrt{-4c\gamma^{2}a}}{2\gamma}=\pm i\sqrt{ca}}

Ou seja, temos apenas a parte imaginária, e retornamos à estabilidade do centro. Dessa forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=0} ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k\neq0} determina se o sistema atinge equilíbrio ou permanece oscilatório, e depois o conjunto de parâmetros, caso atinja estabilidade, determina se ela é atingida com ou sem predadores.

Exemplo

Para estudarmos melhor uma situação, vamos escolher os parâmetros: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle a=1} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha=0.5} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=0.5} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c=0.75} ,Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \gamma=0.5} . Então os pontos de equilíbrio são:

• Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)\rightarrow\lambda=\left\{ 1,-0.75\right\}} , uma sela, instável;
• Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(2,0\right)\rightarrow\lambda=\left\{ -1,0.25\right\}} , outro ponto instável, outra sela;
• Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(1.5,0.5\right)\rightarrow\lambda=\left\{ -0.375+0.22i,-0.375-0.22i\right\}} , agora temos um nó assintoticamente estável, pois as parte reais são negativas e as imaginárias são os conjugados.

E fazendo um rascunho do plano de fases, próximo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} , desprezando então os termos não-lineares:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} a & 0\\ 0 & -c \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & -0.75 \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{c} x\\ -0.75y \end{array}\right)}

Próximo a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{a}{k},0\right)=\left(2,0\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -a & -\frac{\alpha a}{k}\\ & \gamma\frac{a}{k}-c \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -1 & -1\\ & 0.25 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)=\left(\begin{array}{cc} -1 & -1\\ & 0.25 \end{array}\right)\left(\begin{array}{c} x-2\\ y \end{array}\right)=\left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{c} \left(2-x\right)-y\\ 0.25y \end{array}\right)}

De Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)=\left(1.5,0.5\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -\frac{kc}{\gamma} & -\frac{c\alpha}{\gamma}\\ \frac{\gamma a-kc}{\alpha} & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -0.75 & -0.75\\ 0.25 & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)=\left(\begin{array}{cc} -0.75 & -0.75\\ 0.25 & 0 \end{array}\right)\left(\begin{array}{c} x-1.5\\ y-0.5 \end{array}\right)=\left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{c} 0.75\left[\left(1.5-x\right)+\left(0.5-y\right)\right]\\ 0.25\left(x-1.5\right) \end{array}\right)}

Plotando temos então:

A esquerda o rascunho do diagrama de fases, e a direita a evolução do sistema para as condições iniciais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{0},y_{0}\right)=\left(2,0.05\right)} .

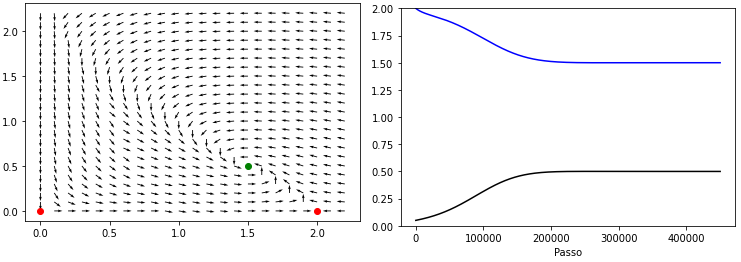
Por curiosidade, se fazemos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=0} : Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} a & 0\\ 0 & -c \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & -0.75 \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)}

E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{a}{\alpha}\right)=\left(1.5,2.0\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} 0 & -\frac{\alpha c}{\gamma}\\ \frac{\gamma a}{\alpha} & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} 0 & -0.75\\ 1 & 0 \end{array}\right)\left(\begin{array}{c} x-1.5\\ y-2 \end{array}\right)=\left(\begin{array}{c} -0.75(y-2)\\ x-1.5 \end{array}\right)} Plotando o resultado:

A direita o rascunho do diagrama de fase, e a esquerda a evolução para as condições iniciais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{0},y_{0}\right)=\left(1,0.5\right)} .

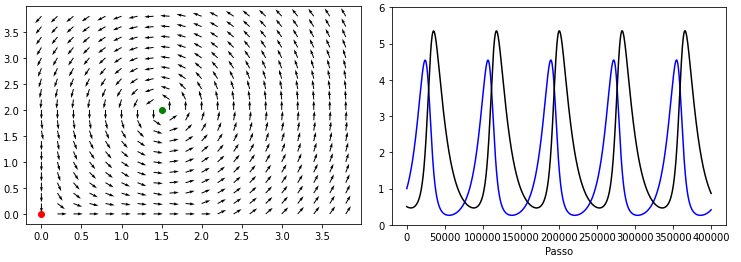
Códigos

Os seguintes códigos escritos em Python foram utilizados para obter a solução numérica e plotar o rascunho do diagrama de fases próximo aos pontos de equilíbrio.

import matplotlib.pyplot as plt
import numpy as np

# LOTKA-VOLTERRA: Solução numérica
# Jhordan Silveira de Borba
# sbjhordan@gmail.com

def sol_lot():
    x=[]
    y=[]
    x.append(1)      # População inicial de presas
    y.append(0.5)    # População inicial de predadores
    N=400000         # Quantidade de passos
    d=0.0001         # Tamanhodos passos
    a=0              # 1: Amortecido, 0: Sem amortecimento
    
    for i in range(N-1):
        x.append(x[i]+d*(x[i]*(1-0.5*y[i])-0.5*x[i]*x[i]*a))
        y.append(y[i]+d*(y[i]*(-0.75+0.5*x[i])))
    #Plotamos a evolução temporal das frações de população
    X=np.arange(len(x)) #Eixo x
    plt.plot(X,x,'b-')
    plt.plot(X,y,'k-')
    plt.xlabel('Passo')
    plt.ylim(0,6)
    plt.show()

A função abaixo tem como finalidade plotar um rascunho do plano de fase próximo ao pontos de equilíbrio do sistema:

import matplotlib.pyplot as plt
import numpy as np

# LOTKA-VOLTERRA: Plano de fase
# Jhordan Silveira de Borba
# sbjhordan@gmail.com

def phase_lot():
    X = np.arange(0, 4, 0.2)  # Eixo x
    Y = np.arange(0, 4, 0.2)  # Eixo Y
    U,V=np.meshgrid(X,Y)
    
    p1=[0.,0.]           # Ponto de equilíbrio 1
    p2=[1.5,2.0]         # Ponto de equilíbrio 2
    p3=[1.5*100,0.5*100] # Ponto de equilíbrio 3
    
    c=0
    for x in X:
        l=0
        for y in Y:
            #Distâncias
            d1=np.sqrt((x-p1[0])*(x-p1[0])+(y-p1[1])*(y-p1[1]))
            d2=np.sqrt((x-p2[0])*(x-p2[0])+(y-p2[1])*(y-p2[1]))
            d3=np.sqrt((x-p3[0])*(x-p3[0])+(y-p3[1])*(y-p3[1]))
            
            #encontrar o ponto de equilíbrio mais próximo
            p=1
            if(d2<d1):
                p=2
                if(d3<d2):
                    p=3
            elif(d3<d1):
                p=3
                
            # Calculamos o vetor de variação do estado baseado no ponto mais próximo:
            # [dx/dt,dy/dt]=[a,b]
            if(p==1):
                a=x  
                b=-0.75*y
            elif(p==2):
                a=-0.75*(y-2)
                b=x-1.5
            elif(p==3):
                a=0.75*((1.5-x)+(0.5-y))
                b=0.25*(x-1.5)
            else:
                print("Algo deu errado")
            m=np.sqrt(a*a+b*b) # Módulo do vetor para normalizar
            if(m==0):
                m=1
            U[l,c]=a/m
            V[l,c]=b/m
            l=l+1
        c=c+1
    
    # Plotamos o resultado
    fig, ax = plt.subplots()
    ax.quiver(X, Y, U, V)      # Os vetores
    plt.plot(p1[0],p1[1],'ro') # O ponto de equilíbrio 1
    plt.plot(p2[0],p2[1],'go') # O ponto de equilíbrio 2
    plt.plot(p3[0],p3[1],'go') # O ponto de equilíbrio 3
    plt.show()

Principais materiais utilizados

1. Numerical Methods (Instituto de Tecnologia de Massachusetts)
2. Numerical Solution of Ordinary Differential Equations (R. Sureshkumar,Instituto de Tecnologia de Massachusetts)
3. A estes materiais, somam-se os vistos em Modelo de Lotka-Volterra

Citações

Anterior: Modelo de Lotka-Volterra | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies I