Modelo de Levins aprimorado para 2 espécies
Anterior: Modelo de Lotka-Volterra amortecido | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies II
Comparação com outros modelos
Para duas espécies, vamos trabalhar com o seguinte sistema de equações:
Onde é a presa e o predador. Podemos comparar com outros modelos. Como um modelo inspirado no modelo de Levins, podemos ver semelhanças bastante fortes desde já. Lembrando do modelo de Levins rapidamente:
O termo na equação da presa é a quantidade de fragmentos disponíveis para a colonização da presa, uma vez que precisamos descontar os fragmentos destruídos, além dos ocupados. Como todos parâmetros são em termos de proporções, temos probabilidade de selecionarmos um fragmento disponível para a colonização da presa. E o termo na equação do predador tem a mesma função, porém agora precisamos lembrar que os fragmentos que o predador pode ocupar são os que já estão ocupados pela presa, descontando os que já possuem predador. Então considerando propriedades de conjuntos, e olhando em termos de probabilidades esta equação, temos a probabilidade de selecionar um fragmento ocupada pela presa, mas precisamos descontar a probabilidade de selecionar um fragmento que também já esteja ocupada por um predador . A maior diferença se dá porque a presa tem um termo a mais correspondendo ao decréscimo da população devido a predação, evento não considerado no modelo de Levins, mas considerado no modelo de Lotka-Volterra.
Por isso a próxima comparação que podemos fazer é com o modelo de Lotka-Volterra amortecido:
Vamos reescrever nosso sistema de equações:
Olhando agora primeiro para a equação da presa, a maior diferença que encontramos, e é que temos o termo de extinção local que não é devido a predação , algo já familiar do modelo de Levins. E já quando olhamos para a equação do predador, temos o termo , podemos pensar também como um termo logístico, impondo um limite na população de predadores, da mesma forma que ocorre com as presas. Porém agora o termo logístico não é uma constante, mas depende também da população de presas.
Análises dos pontos de equilíbrio
Sendo todos o parâmetros como variáveis
Vamos tentar fazer análises parecidas agora. Primeiro buscar os pontos de equilíbrio pro sistema:
Temos então 4 pontos de equilíbrio:
- Primeiro: extinção de ambas as espécies
- Segundo: extinção do predador
Os pontos de equilíbrio com ambas as espécies são extremamente mais complicados. Para o terceiro ponto temos:
E o quarto e último ponto:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=x\left(c_{1}\left(1-D\right)-\mu y\right)-c_{1}x^{2}-e_{1}x} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}=y\left(-e_{y}+c_{y}x\right)-c_{y}xy^{2}}
Separando os termos lineares dos não lineares:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=\left[x\left(c_{1}\left(1-D\right)-e_{1}\right)\right]-\left[\mu yx+c_{1}x^{2}\right]} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}=-\left[ye_{y}\right]+\left[c_{y}xy-c_{y}xy^{2}\right]}
Calculando então os limites:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\mu yx+c_{1}x^{2}}{x\left(c_{1}\left(1-D\right)-e_{1}\right)}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\mu y+c_{1}x}{c_{1}\left(1-D\right)-e_{1}}=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{c_{y}xy-c_{y}xy^{2}}{ye_{y}}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{c_{y}x-c_{y}xy}{e_{y}}=0}
Desprezando os termos não lineares:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} c_{1}\left(1-D\right)-e_{1} & 0\\ 0 & -e_{y} \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)}
Logo um dos autovalores é real, sempre negativo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(-e_{y}\right)} e o segundo é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(c_{1}\left(1-D\right)-e_{1}\right)} . Basicamente se o termo de colonização do guanaco for maior que o da extinção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(c_{1}\left(1-D\right)>e_{1}\right)} , temos dois autovalores de sinais opostos, ou seja, um ponto de instabilidade. Aumentando a taxa de extinção do guanaco (ou a destruição do habitat) passamos a ter Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}\left(1-D\right)<e_{1}} , e a extinção de ambas as espécies. Aqui podemos notar uma diferença dos modelos de Lotka-Volterra: a extinção de ambas as espécies pode ser um ponto de equilíbrio estável. Ou seja nos modelos anteriores o sistema nunca iria para o equilíbrio com extinção total, agora há essa possibilidade dependendo do nível de destruição do sistema.
Para o segundo ponto de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{2},y_{2}\right)=\left(x_{2},0\right)} precisamos fazer a translação: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=x-x_{2}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v=y} .
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left[\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)u+\left(-\mu x_{2}\right)v+\left(-c_{1}x_{2}^{2}-e_{1}x_{2}+\left(1-D\right)x_{2}c_{1}\right)\right]+\left[-\mu uv-c_{1}u^{2}\right]} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\left[\left({\it c_{y}}x_{2}-{\it e_{y}}\right)v\right]+\left[-{\it c_{y}}v^{2}x_{2}-{\it c_{y}}uv^{2}+{\it c_{y}}uv\right]}
Podemos ver facilmente que é semi linear para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{u}} uma vez que ao fazermos os:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}\frac{\text{parte não-linear}}{\text{parte linear}}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{-\mu uv-c_{1}u^{2}}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)u+\left(-\mu x_{2}\right)v}}
Fazendo a substituição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r^{2}=x^{2}+y^{2}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x,y\right)=\left(r\cos\theta,r\sin\theta\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r^{2}\left(-\mu\cos\theta\sin\theta-c_{1}\cos\theta^{2}\right)}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)r\cos\theta+\left(-\mu x_{2}\right)r\sin\theta}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r\left(-\mu\cos\theta\sin\theta-c_{1}\cos\theta^{2}\right)}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)\cos\theta+\left(-\mu x_{2}\right)\sin\theta}=0}
É interessante notar que a parte constante vai zerar. E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{v}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\left[-{\it c_{y}}v^{2}x_{2}-{\it c_{y}}uv^{2}+{\it c_{y}}uv\right]}{\left[\left({\it c_{y}}x_{2}-{\it e_{y}}\right)v\right]}=\frac{\left[-{\it c_{y}}vx_{2}-{\it c_{y}}uv+{\it c_{y}}u\right]}{\left[\left({\it c_{y}}x_{2}-{\it e_{y}}\right)\right]}=0}
Analisando o comportamento linear então na proximidade do ponto de equilíbrio:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1} & -\mu x_{2}\\ 0 & {\it c_{y}}x_{2}-{\it e_{y}} \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} E os autovalores são então:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1}=\left(1-D-\frac{e_{1}}{c_{1}}\right)c_{y}-e_{y}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{2}=e_{1}-\left(1-D\right)c_{1}}
Podemos ver que o segundo autovalor tem uma relação entre a extinção e a colonização dos guanacos, se tivermos um valor suficientemente alto de colonização então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(1-D\right)c_{1}>e_{1}\rightarrow\lambda_{2}<0} . E no primeiro autovalor temos uma relação entre a colonização e morte de predadores, se a morte de predadores for suficientemente alta Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}>\left(1-D-\frac{e_{1}}{c_{1}}\right)c_{y}} então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1}<0} . Com as duas condições satisfeitas, temos um ponto de equilíbrio onde os predadores são extintos, e só restam presas.
E por fim, temos dois pontos que suportam a coexistência entre duas espécies. Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{3},y_{3}\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\begin{array}{c} \left[\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)u+\left(-\mu x_{3}\right)v+\left(-\mu x_{3}y_{3}-c_{1}x_{3}^{2}-e_{1}x_{3}+\left(1-D\right)c_{1}x_{3}\right)\right]+\\ \left[-\mu uv-c_{1}u^{2}\right] \end{array}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\begin{array}{c} \left[\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)u+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)v+\left(c_{y}x_{3}y_{3}-y_{3}^{2}c_{y}x_{3}-e_{y}y_{3}\right)\right]+\\ \left[-2c_{y}uvy_{3}-c_{y}v^{2}x_{3}-c_{y}uv^{2}+c_{y}uv\right] \end{array}} Calculando os limites para verificar o comportamento semi linear:Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}\frac{\text{parte não-linear}}{\text{parte linear}}}
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{u}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{-\mu uv-c_{1}u^{2}}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)u+\left(-\mu x_{3}\right)v}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r^{2}\left(-\mu\cos\theta\sin\theta-c_{1}\cos^{2}\theta\right)}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)r\cos\theta+\left(-\mu x_{3}\right)r\sin\theta}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r\left(-\mu\cos\theta\sin\theta-c_{1}\cos^{2}\theta\right)}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)\cos\theta+\left(-\mu x_{3}\right)\sin\theta}=0}
E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{v}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{-2c_{y}uvy_{3}-c_{y}v^{2}x_{3}-c_{y}uv^{2}+c_{y}uv}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)u+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)v}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r^{2}\left(-2c_{y}\cos\theta\sin\theta y_{3}-c_{y}\sin^{2}\theta x_{3}-c_{y}\cos\theta\sin^{2}\theta+c_{y}\cos\theta\sin\theta\right)}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)r\cos\theta+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)r\sin\theta}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\frac{r\left(-2c_{y}\cos\theta\sin\theta y_{3}-c_{y}\sin^{2}\theta x_{3}-c_{y}\cos\theta\sin^{2}\theta+c_{y}\cos\theta\sin\theta\right)}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)\cos\theta+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)\sin\theta}=0}
Montando a matriz linearizada então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} \left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3} & -\mu x_{3}\\ c_{y}y_{3}-y_{3}^{2}c_{y} & c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3} \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Infelizmente o autovalor é extremamente complexo se vamos considerar todos os parâmetros como variáveis. A partir de agora, vamos trabalhar atribuindo valores numéricos aos parâmetros, exceto o fato de destruição do habitat, que é um parâmetro que estamos interessado em analisar como afeta a dinâmica.
Caso particular 1: Utilizando os parâmetros do artigo
Utilizando o seguinte conjunto de parâmetros
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}=0.1}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{1}=0.025}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}=0.015}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \mu=0.3}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{y}=0.015}
Temos os seguintes pontos de equilíbrio com os respectivos autovalores:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1,k}\in\left\{ -\frac{3}{200},\frac{\left(0.75-D\right)}{10}\right\}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{2},y_{2}\right)=\left(0.75-D,0\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{2,k}\in\left\{ -\frac{12D+3}{800},\frac{\left(D-0.75\right)}{10}\right\}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{3},y_{3}\right)=\left(\frac{-4D-9-\sqrt{16D^{2}+72D+273}}{8},\frac{-4D+\left(\sqrt{16D^{2}+72D+273}+15\right)}{24}\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{3,1}=\frac{23\sqrt{16D^{2}+72D+273}+92D+231-\sqrt{2}\sqrt{\left(1156D+1233\right)\sqrt{16D^{2}+72D+273}+4624D^{2}+23016D+33369}}{3200}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{3,2}=\frac{23\sqrt{16D^{2}+72D+273}+92D+231+\sqrt{2}\sqrt{\left(1156D+1233\right)\sqrt{16D^{2}+72D+273}+4624D^{2}+23016D+33369}}{3200}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{4},y_{4}\right)=\left(\frac{-4D-9+\sqrt{16D^{2}+72D+273}9}{8},\frac{-4D-\left(\sqrt{16D^{2}+72D+273}+15\right)}{24}\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{4,1}=\frac{-23\sqrt{16D^{2}+72D+273}+92D+231-\sqrt{2}\sqrt{\left(-1156D-1233\right)\sqrt{16D^{2}+72D+273}+4624D^{2}+23016D+33369}}{3200}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{4,2}=\frac{-23\sqrt{16D^{2}+72D+273}+92D+231+\sqrt{2}\sqrt{\left(-1156D-1233\right)\sqrt{16D^{2}+72D+273}+4624D^{2}+23016D+33369}}{3200}}
Para o primeiro ponto ele está fixo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} e podemos perceber que um autovalor é negativo e o outro depende se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} é maior ou menor que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.75} . Para fatores de destruição maior, ambos autovalores são negativos e temos um ponto de equilíbrio estável com a extinção de ambas espécies, para fatores de destruição menor, temo um ponto instável.
Para o segundo ponto de equilíbrio, temos novamente uma dependência da relação entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.75} . O próprio pronto vai se aproximando a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} conforme Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} cresce. Além disso para valores em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D<0.75} temos um ponto de equilíbrio estável e para acima deste valores se torna instável. Lembrando que para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D>0.75} o ponto já passa a ter uma população negativa de pumas, o que não faz sentido ecologicamente, enquanto o primeiro ponto de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} se torna estável. Então “recuperamos”o resultado do primeiro ponto de equilíbrio.
Os próximos como pode-se imaginar são mais complicados de se analisar, por isso vamos utilizar gráficos para trabalhar.
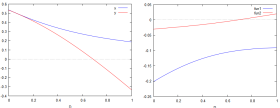
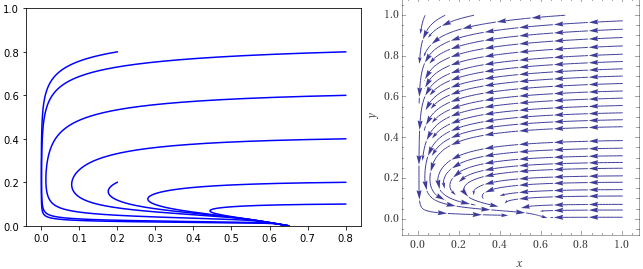
Os dois pontos de equilíbrio tem uma população negativa, e um auto valor positivo, portanto são pontos que não fazem sentido ecologicamente e matematicamente são pontos de equilíbrio instável. Desta forma, o sistema sempre evolui para a extinção de ambas as espécies, como podemos ver no espaço de fazes. Seja calculando a evolução do sistema para diferentes condições inciais, ou fazendo o rascunho do diagrama de fase.
Caso particular 2: Fatores de colonização aumentados
Análogo ao problema do modelo de Levins, este modelo ainda carrega a deficiência de não considerar a configuração espacial. Vamos analisar outro cenário que damos multiplicamos por 4 as taxas de colonização, com o objetivo de analisarmos um cenário em que há coexistência entre presas epredadores.
Repetindo os cálculos temos que o primeiro ponto de equilíbrio é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} , com os autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(-\frac{3}{200},\frac{16}{40}\left(0.9375-D\right)\right)} , então agora para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D<0.9375} , este é um ponto de equilíbrio instável. O segundo ponto de equilíbrio é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(D-0.9375,0\right)} com os autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{48}{800}\left(0.6875-D\right),\frac{16}{40}\left(D-0.9375\right)\right)} , então para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D<0.6875} temos temos o par de sinai dos autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(+,-\right)} , para valores maiores que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D>0.9375} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(-,+\right)} e para valores intermediários Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.6875<D<0.9375} temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(-,-\right)} . O que isso significa?
Bom, para valores maiores que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.9375}
então temos um ponto de equilíbrio instável,e nessa situação o ponto estável é em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)}
ou seja, esperamos o a extinção de de ambas as espécies. Para valores entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.6875<D<0.9375}
temos um ponto de equilíbrio estável, nessa situação, apenas a presa sobrevive. E para valores menores, temos um ponto de equilíbrio instável. E esperamos que os próximos dois pontos de equilíbrio nos ajude a responder o que acontece. Semelhante à discussão anterior, os próximos dois pontos são melhores analisados através de gráficos.
Para o terceiro ponto de equilíbrio, sempre temos população de presas negativas, o que não fez sentido ecologicamente. Esse resultadoé coerente matematicamente pois a parte real dos autovalores são sempre positivos, então é um ponto instável. E por fim, o mais interessante é o quarto ponto de equilíbrio. Para este ponto, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D=0.6875} é exatamente o valor no qual deixa de ser um ponto que ecologicamente faz sentido e também deixa de ser um ponto de equilíbrio estável, e para valores menores que este, tempos um ponto de equilíbrio estável. Então resumidamente, temos
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D<0.6875} : Coexistência de ambas espécies;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.6875<D<0.9375} : Sobrevivência da presa;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.9375<D} : Extinção de todas as espécies.
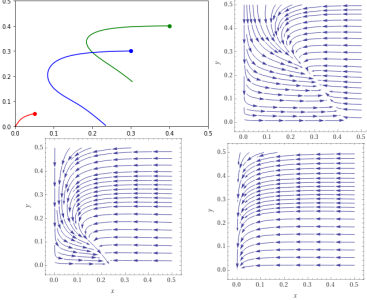
Plotando então a evolução e diagramas de fases para 3 valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.5,0.7,0.96} ), temos:
Códigos
Script para o WxMaxima utilizado para efetuar os cálculos simbólicos necessários para analisar os pontos de equilíbrio considerando todos parâmetros como variáveis:
Cálculos simbólico do modelo de Levins aprimorado para 2 espécies considerando todos parâmetros como variáveis Jhordan Silveira de Borba sbjhordan@gmail.com --> ratprint: false$ Declaração do sistema de equações: --> dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x); dy:(y*(-e_y+c_y*x)-c_y*x*y^2); Soluções e verificação das soluções --> sol:(algsys([dx, dy], [x,y])); N:1;radcan(dx),sol[N][1],sol[N][2]; radcan(dy),sol[N][1],sol[N][2]; Segundo ponto: - Deslocamento - Verificação que a solução linear tem o mesmo ponto de equilíbrio e autovalor - Aqui se a partir de A2 tivermos x_2=x, então x é a posição do ponto de equilíbrio, e não uma variável. --> radcan(dx),x=u+x_2,y=v;radcan(dy),x=u+x_2,y=v; --> B:matrix([u],[v]); A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x; C2:matrix([-c_1*x_2^2-e_1*x_2+(1-D)*x_2*c_1],[0]),x_2=x; radcan(A2.B),u=0,v=0,sol[2][1]; radcan(C2),u=0,v=0,sol[2][1]; radcan(eigenvalues(A2)),sol[2][1]; Terceiro e quarto ponto ponto: - Deslocamento - Verificação que a solução linear tem o mesmo ponto de equilíbrio e autovalor - Aqui se a partir de A3 tivermos x_3=x e y_3=y, então x e y são a posição do ponto de equilíbrio, e não uma variável. --> radcan(dx),x=u+x_3,y=v+y_3;radcan(dy),x=u+x_3,y=v+y_3; --> A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y; C3:matrix([-mu*x_3*y_3-c_1*x_3^2-e_1*x_3+(1-D)*c_1*x_3],[c_y*x_3*y_3-y_3^2*c_y*x_3-e_y*y_3]),x_3=x,y_3=y; radcan(A3.B),u=0,v=0,sol[3][1],sol[3][2]; radcan(C3),u=0,v=0,sol[3][1],sol[3][2]; radcan(C3),u=0,v=0,sol[4][1],sol[4][2]; radcan(eigenvalues(A3)),sol[3][1],sol[3][2];
Script para calcularmos os pontos de equilíbrio e autovalores do sistema tendo a fração de destruição do sistema como única variável:
Análise utilizando como variável apenas D Jhordan Silveira de Borba sbjhordan@gmail.com - Repetimos todos os cálculos substituindo as variáveis pelos valores - Plotamos os gráficos - Obs.: Para obtermos a parte real usamos realpart(%) e a imaginária imagpart(%) --> c_1:0.1;e_1:0.025;e_y:0.015;mu:0.3;c_y:0.015; dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x); dy:(y*(-e_y+c_y*x)-c_y*x*y^2); sol:(algsys([dx, dy], [x,y])); B:matrix([u],[v]); A1:matrix([c_1*(1-D)-e_1,0],[0,-e_y]); A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x; A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y; l1:radcan(eigenvalues(A1)); l2:radcan(eigenvalues(A2)),sol[2][1]; l3:radcan(eigenvalues(A3)),sol[3][1],sol[3][2]; l4:radcan(eigenvalues(A3)),sol[4][1],sol[4][2]; --> X:x,sol[3][1];Y:y,sol[3][2]; wxplot2d([X,Y], [D,0,1],[legend,"x","y"]); wxplot2d([l3[1][1],l3[1][2]], [D,0,1]); X:x,sol[4][1];Y:y,sol[4][2]; wxplot2d([X,Y], [D,0,1],[legend,"x","y"]); wxplot2d([l4[1][1],l4[1][2]], [D,0,1]);
Script para calcularmos os vetores em torno de cada ponto de equilíbrio, para que possamos fazer um rascunho do plano de fase.
Calculo de vetores para o rascunho do plano de fase com D=0.1: Jhordan Silveira de Borba --> D:0.1;c_1:0.1;e_1:0.025;e_y:0.015;mu:0.3;c_y:0.015; dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x); dy:(y*(-e_y+c_y*x)-c_y*x*y^2); sol:(algsys([dx, dy], [x,y])),numer; B:matrix([u],[v]); A1:matrix([c_1*(1-D)-e_1,0],[0,-e_y]); A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x; C2:matrix([-c_1*x_2^2-e_1*x_2+(1-D)*x_2*c_1],[0]),x_2=x; A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y; C3:matrix([-mu*x_3*y_3-c_1*x_3^2-e_1*x_3+(1-D)*c_1*x_3],[c_y*x_3*y_3-y_3^2*c_y*x_3-e_y*y_3]),x_3=x,y_3=y; l1:radcan(eigenvalues(A1)),numer; l2:radcan(eigenvalues(A2)),sol[2][1],numer; l3:radcan(eigenvalues(A3)),sol[3][1],sol[3][2],numer; l4:radcan(eigenvalues(A3)),sol[4][1],sol[4][2],numer; --> radcan((A1.B)); radcan((A2.B)),sol[2][1]; radcan((A3.B)),sol[3][1],sol[3][2]; radcan((A3.B)),sol[4][1],sol[4][2];
Script em Python para plotar o rascunho do diagrama de fases, pode ser editado para visualizarmos só a vizinhança de cada ponto.
# -*- coding: utf-8 -*-
# Modelo aprimorado de Levins para 2 espécies: Diagrama de fases
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
import matplotlib.pyplot as plt
import numpy as np
def phase_lot():
p1=[0.,0.] # Ponto de equilíbrio 1
p2=[0.65,0.] # Ponto de equilíbrio 2
p3=[-3.27,1.31] # Ponto de equilíbrio 3
p4=[0.92,-0.09] # Ponto de equilíbrio 4
X = np.arange(0,1, 0.1/2) # Eixo X
Y = np.arange(0,1, 0.1/2) # Eixo Y
U,V=np.meshgrid(X,Y)
c=0
for x in X:
l=0
for y in Y:
#Distâncias
d=[]
d.append(np.sqrt((x-p1[0])*(x-p1[0])+(y-p1[1])*(y-p1[1])))
d.append(np.sqrt((x-p2[0])*(x-p2[0])+(y-p2[1])*(y-p2[1])))
d.append(np.sqrt((x-p3[0])*(x-p3[0])+(y-p3[1])*(y-p3[1])))
d.append(np.sqrt((x-p4[0])*(x-p4[0])+(y-p4[1])*(y-p4[1])))
for i in range(len(d)):
if (min(d)==d[i]):
p=i
#Calculamos o vetor baseado no ponto mais próximo:
if(p==0):
u=x-p1[0]
v=y-p1[1]
a=(13*u)/200
b=-(3*v)/200
elif (p==1):
u=x-p2[0]
v=y-p2[1]
a=-(70*v+23*u+25)/36
b=-(21*v)/40
elif(p==2):
u=x-p3[0]
v=y-p3[1]
a=(285*v+80*u-5)/29
b=(11*v-10*u)/17
elif(p==3):
u=x-p4[0]
v=y-p4[1]
a=-(47*v+15*u+12)/17
b=(20*v-21*u-66)/18
else:
print("Algo deu errado")
m=np.sqrt(a*a+b*b) # Módulo do vetor
if(m==0):
m=1
# Normalizamos e salvamos o vetor: [dx/dt,dy/dt]=[a,b]
U[l,c]=a/m
V[l,c]=b/m
l=l+1
c=c+1
fig, ax = plt.subplots()
ax.quiver(X, Y, U, V)
plt.plot(p0[0],p0[1],'ko') #Plotamos o primeiro ponto de equilíbrio
plt.plot(p1[0],p1[1],'ko') #Plotamos o segundo ponto de equilíbrio
plt.plot(p3[0],p2[1],'ko') #Plotamos o terceiro ponto de equilíbrio
plt.plot(p4[0],p3[1],'ko') #Plotamos o quarto ponto de equilíbrio
plt.show()
Script em Python para analisar a evolução do sistema no espaço de fases, utilizando o método de Euler:
# -*- coding: utf-8 -*-
# Modelo aprimorado de Levins para 2 espécies: evolução do sistema no espaçode estados
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
def phase2():
#Parâmetros
c1=0.1 # Fator de colonização do guanaco
cy=0.015 # Fator de colonização do puma
e1=0.025 # Fator de extinção local do guanaco
ey=0.015 # Fator de extinção local do puma
u1=0.3 # Fator de predação do guanaco
N=int(200000) # Duração da simulação
d=0.01 # Tamanho do passo
D=0.5 # Destruição do habitat
p1=[0.,0.] # Ponto de equilíbrio 1
p2=[0.65,0.] # Ponto de equilíbrio 2
p3=[-3.26,1.30] # Ponto de equilíbrio 3
p4=[0.92,-0.09] # Ponto de equilíbrio 4
#Valores iniciais:
init=[(0.4,0.4),(0.3,0.3),(0.05,0.05)]
c=0
for it in init:
x=[]
y=[]
x.append(it[0])
y.append(it[1])
for i in range(N-1):
x.append(x[i]+d*(c1*x[i]*(1-D-x[i])-e1*x[i]-u1*x[i]*y[i]))
y.append(y[i]+d*(cy*y[i]*(x[i]-y[i]*(x[i]))-ey*y[i]))
if(c==0):
plt.plot(x,y,'g-')
plt.plot(it[0],it[1],'go')
D=0.7
elif (c==1):
plt.plot(x,y,'b-')
plt.plot(it[0],it[1],'bo')
D=0.95
else:
plt.plot(x,y,'r-')
plt.plot(it[0],it[1],'ro')
c=c+1
plt.plot(p1[0],p1[1],'ko')
plt.plot(p2[0],p2[1],'ko')
plt.plot(p3[0],p3[1],'ko')
plt.plot(p4[0],p4[1],'ko')
plt.xlim(0,0.5)
plt.ylim(0,0.5)
plt.show()
Principal material utilizado
- Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances (Fabiana Laguna e outros, Ecological Modelling)
Anterior: Modelo de Lotka-Volterra amortecido | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies II












![{\displaystyle {\begin{array}{cc}x\left[\left(c_{1}\left(1-D\right)-\mu y\right)-c_{1}x-e_{1}\right]&=0\\y\left[\left(-e_{y}+c_{y}x\right)-c_{y}xy\right]&=0\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3347106e5a4f0c4a7b12713f9d73b8c2cc4654)