Simulação e modelo de campo médio: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[Sistemas de equações diferenciais com atrasos fixos - SIRS | Exemplo: sistema de equações diferenciais com retardo (SIRS) ]] |[[Contexto | Contexto ecológico]]}} | |||
Uma teoria de campo médio em redes complexas pode ser definida como como uma teoria em que se assume que os elementos da rede interagem com igual força com qualquer outro elemento da rede. Olhando para o [[Modelo espacialmente explícito|modelo de 2 presas e 1 predador]], supondo uma grade <math display="inline">3\times3</math> tendo <math display="inline">D=3/9</math> dos fragmento destruídos, um estado possível da rede, em uma representação de grafos, poderia ser: | Uma teoria de campo médio em redes complexas pode ser definida como como uma teoria em que se assume que os elementos da rede interagem com igual força com qualquer outro elemento da rede. Olhando para o [[Modelo espacialmente explícito|modelo de 2 presas e 1 predador]], supondo uma grade <math display="inline">3\times3</math> tendo <math display="inline">D=3/9</math> dos fragmento destruídos, um estado possível da rede, em uma representação de grafos, poderia ser: | ||
| Linha 336: | Linha 339: | ||
* [https://youtu.be/Kt4DUq9mgKQ?t=2476 Minicurso de Redes complexas] (Silvio Ferreira, ENMM-Covid19) | * [https://youtu.be/Kt4DUq9mgKQ?t=2476 Minicurso de Redes complexas] (Silvio Ferreira, ENMM-Covid19) | ||
{{Ecologia| [[Sistemas de equações diferenciais com atrasos fixos - SIRS | Exemplo: sistema de equações diferenciais com retardo (SIRS) ]] |[[Contexto | Contexto ecológico]]}} | |||
Edição das 18h32min de 16 de junho de 2021
Anterior: Exemplo: sistema de equações diferenciais com retardo (SIRS) | Índice: Ecologia | Próximo: Contexto ecológico
Uma teoria de campo médio em redes complexas pode ser definida como como uma teoria em que se assume que os elementos da rede interagem com igual força com qualquer outro elemento da rede. Olhando para o modelo de 2 presas e 1 predador, supondo uma grade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 3\times3}
tendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D=3/9}
dos fragmento destruídos, um estado possível da rede, em uma representação de grafos, poderia ser:

Onde cada elemento representa um fragmento da grade que não está destruído. Por questões de representação foi omitido, mas é importante lembrar que cada elemento da rede pode interagir também consigo mesmo. Então cada fragmento da grade, ou elemento desta rede, pode estar livre ou ocupado pelas espécies, com qualquer uma das combinações possíveis de ocupação. Podemos perceber que não é um modelo de campo médio. Para compreender melhor os modelos de campo médio que são propostos, vamos tentar construir um modelo de rede que se aproxime melhor do que é proposto no campo campo médio, isto é, utilizar as considerações do mesmo na construção da rede. O principal componente é ignorar a distribuição espacial das espécies. Uma representação em grafo deste nova rede poderia por exemplo:
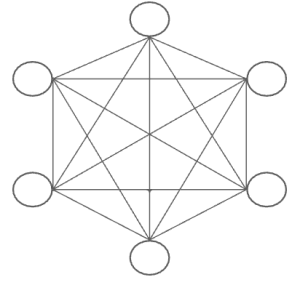
Ou seja, qualquer elemento pode interagir com qualquer outro, não há mais a restrição de distância como no modelo original. Na prática, durante a implementação então será considerado que cada agente pode colonizar qualquer outro agente da rede, assim como o predador pode predar qualquer presa na rede, de forma análoga o competidor superior também pode deslocar qualquer competidor inferior. Basicamente os eventos síncronos serão os seguintes:
- Colonização: para cada elemento ocupado pela espécie Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} , sorteia-se um outro elemento aleatoriamente, se este for disponível para colonização, a probabilidade desta ocorrer é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{\alpha}} .
- Extinção local: se o elemento estiver colonizado pela espécie Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} ,há uma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{\alpha}} de ocorrer extinção local desta espécie.
- Predação: para cada elemento ocupado pelo predador sorteia-se outros dois elementos aleatoriamente, cada um dos elementos sorteados tem como alvo uma espécie Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} diferente. Em ambos os casos então, se o elemento sorteado este estiver ocupado pela presa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} , a predação pode ocorrer com uma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \mu_{\alpha}} .
- Deslocamento competitivo: para cada elemento ocupado pelo competidor superior sorteia-se outro elemento aleatoriamente, se este estiver ocupado pelo competidor inferior então há uma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{1}} de ocorrer a remoção do competidor inferior..
A proposta acima consiste de que em cada passo seja percorrido cada elemento da rede. Então para cada elemento realiza-se as 4 etapas anteriores de maneira síncrona de acordo com a ocupação da mesma. Outra proposta seria para cada passo, realizar apenas uma vez cada uma das etapas. Então nesta proposta quando envolver a interação entre duas espécies sorteia-se os dois elementos aleatoriamente, e quando envolver apenas uma espécie apenas um elemento é sorteado.
Um detalhe importante é a quantidade de conexões que cada agente pode ter. Por exemplo, na simulação original uma espécie Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} ocupando um fragmento, poderia colonizar os 4 fragmentos primeiro-vizinhos (desde que estivessem disponível). Nesta proposta, cada vez que estamos avaliando a dinâmica de um elemento com uma espécie, avaliamos se ocorreu ou não a colonização em um único outro elemento. Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k_{i}} quantidade de conexões possíveis em um elemento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i} , poderíamos considerar que a probabilidade de um agente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i} se conectar com um agente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle j} seja dado por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle A_{ij}=\frac{k_{i}k_{j}}{N_{k}}} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N} é a quantidade total de conexões que existem na rede.
Comparando este modelo proposto, com o seguinte modelo de campo médio:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dx_{1}}{dt}= & c_{1}x_{1}\left(1-D-x_{1}\right)-e_{1}x_{1}-\mu_{1}x_{1}y\\ \frac{dx_{2}}{dt}= & x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu_{2}y+c_{1}x_{1}\right)\right]\\ \frac{dy}{dt}= & y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right]\end{align}}
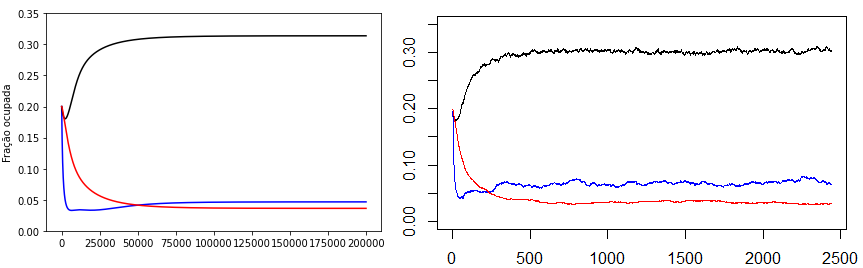
Tem-se então, para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D=0.4} :
Observa-se um comportamento bastante semelhante. A mesma ideia foi trabalhada com o modelo de 2 herbívoros com dinâmica de fragmentos . Neste caso o modelo de campo médio é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{x}_{1}= & c_{1}\left(h-x_{1}\right)x_{1}-e_{1}x_{1}\\ \dot{x}_{2}= & c_{2}\left(h-x_{1}-x_{2}+x_{1}x_{2}\right)x_{2}-e_{2}x_{2}\\ \dot{h}= & -\gamma x_{2}\left(t-\tau_{0}\right)h\left(t-\tau_{0}\right)+\gamma x_{2}\left(t-\tau_{0}-\tau_{r}\right)h\left(t-\tau_{0}-\tau_{r}\right)\end{align}}
A dinâmica de colonização e deslocamento é essencialmente a mesma do modelo interior, a novidade concentra-se na dinâmica dos fragmentos. Após o instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{0}} , quando percorre-se a rede no passo atual Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle n} para avaliar a dinâmica de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{1}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{2}} , ao mesmo tempo explora-se a rede no passo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle n-\tau_{0}} (no passado), onde caso o elemento esteja ocupado por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{2}} , então seleciona-se outro elemento aleatoriamente e uma vez que este represente um fragmento não destruído, há uma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \gamma} de que seja destruído. De modo análogo após o instante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau} avalia-se a rede atrasada no passo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle n-\tau} , e novamente caso o elemento esteja ocupado pela espécie Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{2}} , seleciona-se outro elemento aleatoriamente, porém agora caso este esteja destruído, então há a probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} de ser recuperado. O resultado desta etapa da dinâmica de fragmentos, seja a destruição ou a recuperação do fragmento, é aplicado na rede atual em algum elemento aleatório.
Quando foi implementado este modelo proposto, pode-se perceber um comportamento qualitativo próximo, mas menos semelhante que o caso anterior. A principal diferença parece ser pelo comportamento das ovelhas. Um dos motivos que pode ser, é que quando olhamos o termo de colonização das ovelhas no modelo de campo médio, a componente referente à quantidade de fragmento disponíveis para colonização éFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(h-x_{1}-x_{2}+x_{1}x_{2}\right)} . Isto decorre porque precisamos descontar não só o fragmento disponívis, mas também os fragmentos que estão ocupados por ovelhas ou guanacos. A a probabilidade de selecionar um fragmento ocupado por um ou outro é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle P\left(x_{1}\cup x_{2}\right)=P\left(x_{1}\right)+P\left(x_{2}\right)-P\left(x_{1}\cap x_{2}\right)} , como foi considerado eventos independentes, então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle P\left(x_{1}\cap x_{2}\right)=x_{1}x_{2}} . Porém conforme a dinâmica evolui, a distribuição das ovelhas e dos guanacos não é mais completamente aleatório e independente, pois as ovelhas não podem ocupar fragmentos já ocupados por guanacos. Isto é, a quantidade de fragmentos ocupados por ovelhas e guanacos na simulação é menor do que o previsto considerando que sejam eventos aleatórios. Conforme a ocupação dos fragmentos se aproxima de 100% e a população de guanaco cresce, as ovelhas encontram menos fragmento disponíveis para colonizar do que o previsto pelo campo médio.
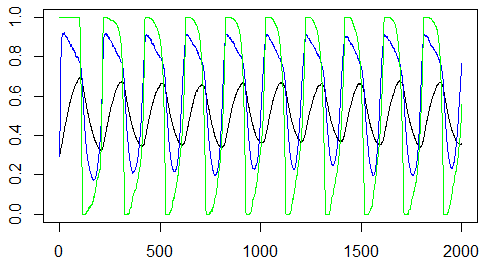
Por isto foi adicionado uma etapa de ’espalhamento’ no começo de cada passo, ou seja todos os indivíduos são aleatoriamente redistribuídos ao longo da rede, inclusive os fragmentos destruídos também são redistribuídos. Desta forma obteve-se os eguinte resultado:
Pode-se observar que o resultado se aproxima melhor do modelo de campo médio que o resultado anterior. Caso houvesse interesse em aproximar ainda mais os modelos, uma sugestão seria explorar a quantidade de conexões entre os fragmentos de uma forma mais elaborada ou ainda a relação entre a passagem do tempo nas equações diferenciais e na simulação. Mas acredito que neste momento já foi demonstrado semelhanças suficientes entre os modelos. Para esta simulação foi adotado o equivalente a 2 passos no modelo de agentes como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 1t} , por exemplo, no sistema de equações foi utilizado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{0}=50\left[\text{tempo}\right]} e no modelo de agentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau_{0}=100\left[\text{passos}\right]} , mas manteve-se a mesma razão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{\tau_{0}}{\tau_{r}}} .
Códigos
Os códigos referente à solução dos sistemas de equações diferenciais estão disponíveis nas respectivas páginas. Sobre as redes, ambos os códigos foram desenvolvidos em Python, e para a primeira rede discutida o código utilizado foi:
# -*- coding: UTF-8 -*-
# "Rede média" para o modelo de 2 herbívoros e um carnívoro
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
#Bibliotecas
import numpy as np # Biblioteca de funções matemáticas
import copy # Biblioteca com funções para copiar
import random # Biblioteca para gerar números aleatórios
#CONDIÇÕES INICIAIS ------------------------------------------------------
maxt = 5000 #tiempo total de cada realizacion
Lx = 200 #tamaño del sustrato
Ly = 200
#Fracciones iniciales
D = 0.4 #fraccion inicial de sitios destruidos
x10 = 0.2 #fraccion inicial de sitios libres ocupados por x1
x20 = 0.2 #fraccion inicial de sitios libres ocupados por x2
y0 = 0.2 #fraccion inicial de sitios ocupdos por guanacos e ovelhas ocupados por y
#Tasas
M=4
cx1 = M*0.05 #colonizaciones
cx2 = M*0.1
cy = M*0.015
ex1 = 0.05 #extinciones
ex2 = 0.01
ey = 0.02
mx1y = 0.2 #depredaciones
mx2y = 0.8
con=1 #controle de registro
#Inicializaciones
s = np.full((Lx, Ly), [1]) #matriz de habitat (1=sitio disponible, 0=destruido)
x1 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
x2 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
y = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
#Colonização inicial
for i in range(1,Lx-1):
for j in range (1,Ly-1):
if (np.random.rand() < D): s[i,j]=0
if (np.random.rand() < x10/(1-D) and s[i,j]==1): x1[i,j]=1
if (np.random.rand() < x20/(1-D) and s[i,j]==1): x2[i,j]=1
if (np.random.rand() < y0/(1-D) and s[i,j]==1): y[i,j]=1
for i in range(Lx): #destruimos los bordes del habitat
s[i,0]=0
s[i,Ly-1]=0
for j in range(Ly):
s[0,j]=0
s[Lx-1,j]=0
#Lazo temporal
fx1=sum(sum(x1))/((Lx)*(Ly))
fx2=sum(sum(x2))/((Lx)*(Ly))
fy =sum(sum(y)) /((Lx)*(Ly))
f = open("redemedia2015.dat", "w")
f.write(" "+str(0)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n")
for it in range(maxt):
if (float(it)%(float(maxt)/100)==0.):
print("Porcentagem: "+str(it*100/maxt)) # Exibe o passo atual
x1old=copy.copy(x1) #poblaciones del paso anterior
x2old=copy.copy(x2)
yold=copy.copy(y)
for i in range (1,Lx-1):
for j in range (1,Ly-1):
# COLONIZAÇÃO+++++++++++++++++++++++++++++++++++++++++++++++++++++
if (s[i,j]==0):
for c in range(1):
m=random.randint(1,Lx-1)
n=random.randint(1,Ly-1)
if (s[m,n]==1 and x1old[m,n]==0):
if (np.random.rand()<= cx1):
x1[m,n]=1
# Ovelha
if (x2old[i,j]==1):
for c in range(1):
m=random.randint(1,Lx-1)
n=random.randint(1,Ly-1)
if (s[m,n]==1 and (x1old[m,n]==0 and x2old[m,n]==0)):
if (np.random.rand()<= cx2):
x2[m,n]=1
# Puma
if (yold[i,j]==1):
for c in range(1):
m=random.randint(1,Lx-1)
n=random.randint(1,Ly-1)
if (x1old[m,n]==1 or x2old[m,n]==1):
if (np.random.rand()<= cy):
y[m,n]=1
#EXTINÇÃO LOCAL++++++++++++++++++++++++++++++++++++++++++++++++++++
#Guanaco
if (x1old[i,j]==1):
if (np.random.rand()<= ex1):
x1[i,j]=0
#Ovelha
if (x2old[i,j]==1):
if (np.random.rand()<= ex2):
x2[i,j]=0
#Puma
if (yold[i,j]==1):
if (np.random.rand()<= ey):
y[i,j]=0
#PREDAÇÃO++++++++++++++++++++++++++++++++++++++++++++++++++++++++
if (x1old[i,j]==1):
m=random.randint(1,Lx-1)
n=random.randint(1,Ly-1)
if (yold[m,n]==1):
if (np.random.rand()<= mx1y):
x1[i,j]=0
if(x2old[i,j]==1):
m=random.randint(1,Lx-1)
n=random.randint(1,Ly-1)
if (yold[m,n]==1):
if (np.random.rand()<= mx2y):
x2[i,j]=0
#DESLOCAMENTO+++++++++++++++++++++++++++++++++++++++++++++++++++
if (x2old[i,j]==1):
m=random.randint(1,Lx-1)
n=random.randint(1,Ly-1)
if ( x1old[m,n]==1):
if (np.random.rand()<= cx1):
x2[i,j]=0
if(con==1):
fx1=sum(sum(x1))/((Lx)*(Ly))
fx2=sum(sum(x2))/((Lx)*(Ly))
fy =sum(sum(y)) /((Lx)*(Ly))
f.write(" "+str(it+1)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n")
con=0
con=con+1
# CÁLCULOS FINAIS -----------------------------------------------------
f.close()
E para a segunda rede, tivemos as duas tentativas foram:
# -*- coding: UTF-8 -*-
# "Rede média" para o modelo de 2 herbívoros com dinâmica dos fragmentos
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
#Bibliotecas
import numpy as np # Biblioteca de funções matemáticas
import copy # Biblioteca com funções para copiar
import random # Biblioteca para gerar números aleatórios
#CONDIÇÕES INICIAIS ------------------------------------------------------
maxt = 500 #tiempo total de cada realizacion
Lx = 100 #tamaño del sustrato en la coordenada x
Ly = 100
#Fracciones iniciales
x10 = 0.3 #fraccion inicial de sitios ocupados por x1
x20 = 0.3 #fraccion inicial de sitios ocupados por x2
h0 = 1. #fraccion inicial de sitios disponibles
#Tasas
cx1 = 0.04 #colonizaciones
cx2 = 0.7
ex1 = 0.01 #extinciones
ex2 = 0.01
to = 100 #Tempo de ocupação
tr = 20 #Tempo de recuperação
g = 0.1 #Taxa de variação dos fragmentos
t = tr+to
con1=1 #Controle do registro
#Inicializaciones
sh =[] # Histórico da matriz de habitat
x2h=[] # Histórico da matriz de ovelhas
s = np.full((Lx, Ly), [1]) # matriz de habitat (1=sitio disponible, 0=destruido)
x1 = np.full((Lx, Ly), [0]) # 1 = sitio ocupado, 0 sitio vazio
x2 = np.full((Lx, Ly), [0]) # 1 = sitio ocupado, 0 sitio vazio
sh.append(s)
x2h.append(x2)
for i in range(Lx): # Distribuição inicial
for j in range (Ly):
if (np.random.rand() < (1-h0) ): s[i,j]=0
if (np.random.rand() < x10/h0 and s[i,j]==1): x1[i,j]=1
if (np.random.rand() < x20/h0 and s[i,j]==1): x2[i,j]=1
#Lazo temporal
fx1=sum(sum(x1))/((Lx)*(Ly))
fx2=sum(sum(x2))/((Lx)*(Ly))
fs =sum(sum(s)) /((Lx)*(Ly))
f = open("temporal2019.dat", "w")
f.write(" "+str(0)+" "+str(fx1)+" "+str(fx2)+" "+str(fs)+"\n")
for it in range(maxt):
if (float(it)%(float(maxt)/100)==0.):
print("Porcentagem: "+str(it*100/maxt)) # Exibe o passo atual
#ESPALHAMENTO
nx1=sum(sum(x1))
nx2=sum(sum(x2))
ns =sum(sum( s))
s = np.full((Lx, Ly), [0]) # matriz de habitat (1=sitio disponible, 0=destruido)
x1 = np.full((Lx, Ly), [0]) # 1 = sitio ocupado, 0 sitio vazio
x2 = np.full((Lx, Ly), [0]) # 1 = sitio ocupado, 0 sitio vazio
for i in range (max(nx1,nx2,ns)): #Quantidade máxima de animais que vamos espalhar
if(i<ns): #Esoalhando os fragmentos
(a,b)=(random.randint(0,Lx-1),random.randint(0,Ly-1))
while(True):
if(s[a,b]==0): #Se escolhemos um fragmento destruído
s[a,b]=1 #Revitalizamos
break #E saímos do loop
else: #Se não repetimos
(a,b)=(random.randint(0,Lx-1),random.randint(0,Ly-1))
if(i<nx1): #Competidor superior
(a,b)=(random.randint(0,Lx-1),random.randint(0,Ly-1))
while(True):
if(x1[a,b]==0):
x1[a,b]=1
break
else:
(a,b)=(random.randint(0,Lx-1),random.randint(0,Ly-1))
if(i<nx2): #Competidor inferior
(a,b)=(random.randint(0,Lx-1),random.randint(0,Ly-1))
while(True):
if(x2[a,b]==0):
x2[a,b]=1
break
else:
(a,b)=(random.randint(0,Lx-1),random.randint(0,Ly-1))
sold =copy.copy(s )
x1old=copy.copy(x1) #poblaciones del paso anterior
x2old=copy.copy(x2)
for i in range (0,Lx-1):
for j in range (0,Ly-1):
#COLONIZAÇÃO+++++++++++++++++++++++++++++++++++
#Guanaco
if (x1old[i,j]==1):
for a in range(1):
m=random.randint(0,Lx-1)
n=random.randint(0,Ly-1)
if (sold[m,n]==1 and x1old[m,n]==0):
if (np.random.rand()<= cx1):
x1[m,n]=1
#Ovelha
if (x2old[i,j]==1):
for a in range(1):
m=random.randint(0,Lx-1)
n=random.randint(0,Ly-1)
if (sold[m,n]==1 and (x1old[m,n]==0 and x2old[m,n]==0)):
if (np.random.rand()<= cx2):
x2[m,n]=1
#EXTINÇÃO
#Guanaco
if (x1old[i,j]==1):
if (np.random.rand()<= ex1):
x1[i,j]=0
#Ovelha
if (x2old[i,j]==1):
if (np.random.rand()<= ex2):
x2[i,j]=0
#DESLOCAMENTO+++++++++++++++++++++++++++++++++++++++++++++++++++
if (x2old[i,j]==1):
m=random.randint(0,Lx-1)
n=random.randint(0,Ly-1)
if ( x1old[m,n]==1):
if (np.random.rand()<= cx1):
x2[i,j]=0
#Dinâmica dos patches+++++++++++++++++++++++++++++++++++++++++++
if(it+2>to): #Se passou o primeiro período de ocupação
if (x2h[to-1][i,j]==1): #Então há destruição de fragmentos
m=random.randint(0,Lx-1)
n=random.randint(0,Ly-1)
if (sh[to-1][m,n]==1):
if(np.random.rand()<=g):
li=np.where(s==1) #Elementos que são 1
if(len(li[0])==1):
k=0
elif(len(li[0])>1):
k=random.randint(0,len(li[0])-1) #Sorteio do elemento
s[li[0][k],li[1][k]]=0
if(it+2>t): #Se passou do período de oucpação e recuperação
if (x2h[t-1][i,j]==1): #Há recuperação do habitat
m=random.randint(0,Lx-1)
n=random.randint(0,Ly-1)
if (sh[t-1][m,n]==1):
if(np.random.rand()<=g):
li=np.where(s==0)
if (len(li[0])==1):
k=0
elif(len(li[0])>1):
k=random.randint(0,len(li[0])-1)
s[li[0][k],li[1][k]]=1
sh.insert(0,copy.copy(s)) #Adiciona o estado atual no histórico
x2h.insert(0,copy.copy(x2))
if (it>=t): #Exclui estados que não serão mais utilizados
sh.pop()
x2h.pop()
if (con1==1):
fx1=sum(sum(x1))/((Lx)*(Ly))
fx2=sum(sum(x2))/((Lx)*(Ly))
fs =sum(sum(s ))/((Lx)*(Ly))
f.write(" "+str(it+1)+" "+str(fx1)+" "+str(fx2)+" "+str(fs)+"\n")
con1=0
con1=con1+1
f.close()
Principais materiais utilizados
- Minicurso de Redes complexas (Silvio Ferreira, ENMM-Covid19)
Anterior: Exemplo: sistema de equações diferenciais com retardo (SIRS) | Índice: Ecologia | Próximo: Contexto ecológico