Modelo espacialmente explícito para 2 espécies
Anterior: Modelo de Levins aprimorado para 2 espécies II | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 3 espécies
Em um primeiro momento, é importante lembrar que este modelo foi construído para ser coerente com o contexto ecológico da região norte da Patagônia. Neste modelo, busca-se modelar a interação entre dois herbívoros que competem de forma hierárquica entre si, considerando também a dinâmica de degradação e recuperação do ambiente. Esta dinâmica do ambiente é fruto da interação surgida da competição entre as espécies.
A degradação de um fragmento diz especificamente sobre a quantidade de recursos naturais disponíveis pra a sobrevivência de herbívoros. Os guanacos e as ovelhas são responsáveis por impactar no ambiente, porém como o guanaco evoluiu com a flora, e seu consumo sobre condições naturais permite um consumo sustentável, vamos considerar seu impacto como negligenciável. Assim temos as ovelhas (devido a atividade pecuária humana) sendo responsável pelo impacto ambiental.
Dessa forma temos como principais características do modelo:
- Guanaco, o competir superior:
- Qualquer fragmento que não esteja destruído nem já ocupado por guanacos, está disponível para ocupação pelos primeiros vizinhos ocupados por guanacos com uma probabilidade ;
- Podem ser extinto localmente em cada fragmento ocupado com uma probabilidade ;
- Ovelha, o competidor inferior:
- Qualquer fragmento que não esteja destruído e nem ocupado por nenhuma espécie está disponível para colonização de ovelhas que ocupam fragmentos primeiros vizinhos com uma probabilidade
- Pode ser extinta localmente por deslocamento competitivo quando em um mesmo fragmento coexistem com guanacos com uma probabilidade ;
- Podem ser extinto localmente em cada fragmento ocupado com uma probabilidade .
E por fim, a dinâmica dos fragmentos :
- Quando um fragmento é ocupado por uma ovelha, dispara um relógio interno, após passos o fragmento é considerado destruído, e todas as populações ocupando o fragmento são extintas localmente;
- Se a ovelha for extinta localmente antes de atingir , o relógio interno é zerado.
- Após ser considerado destruído, é disparado novamente o relógio interno, e então após passos o fragmento é considerado disponível novamente
A simulação ocorre em uma grade , onde um fragmento na posição é considerado ocupado pela espécie se , de modo análogo, o fragmento é considerado disponível se . Ao final de cada passo calculamos a fração ocupada por cada espécie:
Pois as bordas são consideradas permanentemente destruídas. Para o cálculo é análogo.
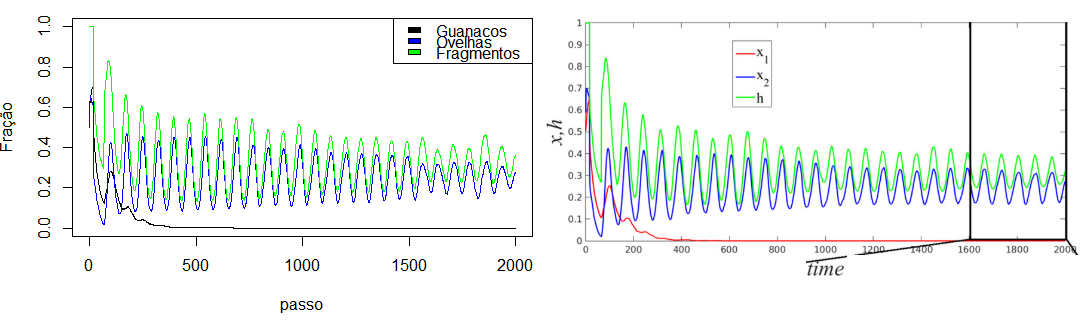
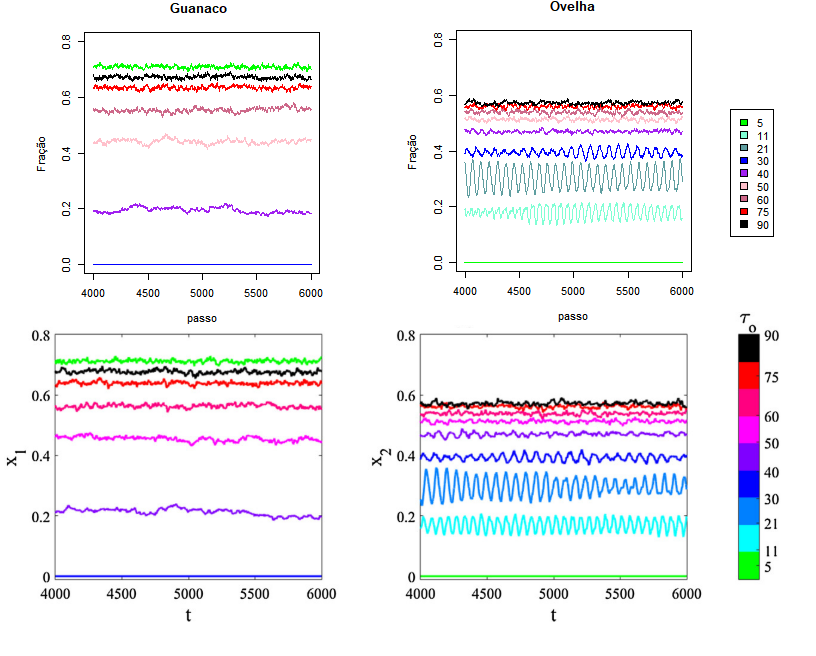
Resultados
Comparando o resultado obtido pelo código abaixo com os resultados apresentados originalmente no artigo utilizado como material principal, temos:
Código
# -*- coding: UTF-8 -*-
# Modelo espacialmente explícito para 2 espécies
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
#Bibliotecas
import numpy as np # Biblioteca de funções matemáticas
import copy # Biblioteca com funções para copiar
#CONDIÇÕES INICIAIS ------------------------------------------------------
maxt = 6000 #tiempo total de cada realizacion
Lx = 100 #tamaño del sustrato en la coordenada x
Ly = 100
#Fracciones iniciales
x10 = 0.6 #fraccion inicial de sitios ocupados por x1
x20 = 0.5 #fraccion inicial de sitios ocupados por x2
#Tasas
cx1 = 0.05 #colonizaciones
cx2 = 0.5
ex1 = 0.05 #extinciones
ex2 = 0.01
to = 50 #Período de ocupação
tr = 17 #Período de recuperação
#Inicializaciones
c = np.full((Lx, Ly), [0]) # Relógio interno
s = np.full((Lx, Ly), [1]) # matriz de habitat (1=sitio disponible, 0=destruido)
x1 = np.full((Lx, Ly), [0]) # 1 = sitio ocupado, 0 sitio vazio
x2 = np.full((Lx, Ly), [0]) # 1 = sitio ocupado, 0 sitio vazio
# Destruimos los bordes del habitat
for i in range(Lx):
s[i,0]=0
s[i,Ly-1]=0
for j in range(Ly):
s[0,j]=0
s[Lx-1,j]=0
# Distribui a população inicial de herbívoros
for i in range(1,Lx-1):
for j in range (1,Ly-1):
rnd=np.random.rand()
if (rnd < x10 and s[i,j]==1): x1[i,j]=1
rnd=np.random.rand()
if (rnd < x20 and s[i,j]==1): x2[i,j]=1
#-------------------------------------------------------
#Lazo temporal
fx1=sum(sum(x1))/((Lx-2)*(Ly-2))
fx2=sum(sum(x2))/((Lx-2)*(Ly-2))
fs =sum(sum(s)) /((Lx-2)*(Ly-2))
f = open("temporal2019.dat", "w")
f.write(" "+str(0)+" "+str(fx1)+" "+str(fx2)+" "+str(fs)+"\n")
for it in range(maxt):
if (float(it)%(float(maxt)/100)==0.):
print("Porcentagem: "+str(it*100/maxt)) # Exibe o passo atual
sold=copy.copy(s) # Distribuição de fragmentos do passo anterior
x1old=copy.copy(x1) # Poblaciones del paso anterior
x2old=copy.copy(x2)
#Recorro la malla
for i in range (1,Lx-1):
for j in range (1,Ly-1):
#Colonizaciones
if (x1old[i,j]==0 and s[i,j]==1): #colonizacion de x1 si el sitio esta libre de x1 y no destruido:
nvec=x1old[i-1,j]+x1old[i+1,j]+x1old[i,j-1]++x1old[i,j+1] #cantidad de vecinos ocupados
p=1.0-(1.0-cx1)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre
rnd=np.random.rand()
if (rnd < p):x1[i,j]=1
if (x2old[i,j]==0 and s[i,j]==1 and x1old[i,j]==0): #colonizacion de x2 si el sitio esta libre de x1 y x2, y no destruido:
nvec=x2old[i-1,j]+x2old[i+1,j]+x2old[i,j-1]+x2old[i,j+1] #cantidad de vecinos ocupados
p=1.0-(1.0-cx2)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre
rnd=np.random.rand()
if (rnd < p): x2[i,j]=1
#extinciones
if (x1old[i,j]==1): #extincion de x1 si el sitio esta ocupado
rnd=np.random.rand()
if (rnd < ex1): x1[i,j]=0
if (x2old[i,j]==1): #extincion de x2 si el sitio esta ocupado
rnd=np.random.rand()
if (rnd < ex2):
x2[i,j]=0
c[i,j]=0
#desplazamiento por competencia (jerarquia)
if (x1old[i,j]==1 and x2old[i,j]==1):
rnd=np.random.rand()
if (rnd < cx1):
x2[i,j]=0
c[i,j]=0
#Atualização dos relógios internos
if (x2old[i,j]==1): # Se está ocupado por ovelhas
c[i,j]=c[i,j]+1 # Avança o relógio interno
if (c[i,j]==to): # Se agintiu o período máximo de ocupação
c[i,j]=0 # Exingue todas espécies e reseta o relógio, e torna o fragmento indisponível
s[i,j]=0
x1[i,j]=0
x2[i,j]=0
elif (sold[i,j]==0): # Se está destruído
c[i,j]=c[i,j]+1 # Avança o relógio intenro
if (c[i,j]==tr): # Se atingiu o período de recuperação
c[i,j]=0 # REseta o relógio e torna o fragmento disponível
s[i,j]=1
fx1=sum(sum(x1))/((Lx-2)*(Ly-2))
fx2=sum(sum(x2))/((Lx-2)*(Ly-2))
fs =sum(sum(s)) /((Lx-2)*(Ly-2))
f.write(" "+str(it+1)+" "+str(fx1)+" "+str(fx2)+" "+str(fs)+"\n")
f.close
Principal material utilizado
- Waves of desertification in a competitive ecosystem (Y. C. Daza C. e outros, Ecological Modelling)
Anterior: Modelo de Levins aprimorado para 2 espécies II | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 3 espécies