Modelo de Lotka-Volterra

Anterior: Métodos de Lyapunov | Índice: Ecologia | Próximo: Modelo de Lotka-Volterra amortecido

No modelo de Lotka-Volterra temos as seguintes considerações:

• Na ausência de predadores, a população de presas aumenta a uma taxa proporcional à população atual;
• Na ausência de presas, os predadores irão à extinção;
• O número de encontro entre presas e predadores é proporcional a produto das duas populações.
  • Estes encontros beneficiam os predadores em detrimento das presas.

Dessa forma, as equações são:

• ${\textstyle {\frac {dx}{dt}}=x\left(a-\alpha y\right)}$
• ${\textstyle {\frac {dy}{dt}}=y\left(-c+\gamma x\right)}$

Onde:

• ${\textstyle a:}$ taxa de crescimento de presas sem predadores;
• ${\textstyle \alpha :}$taxa de decréscimo da população de presas devido a predação;
• ${\textstyle c:}$ taxa de mortalidade da população de predadores sem presas;
• ${\textstyle \gamma }$: taxa de crescimento de predadores devido a predação.

Separação de variáveis

Utilizando a separação de variáveis, temos:

$${\frac {dy}{dt}}{\frac {dt}{dx}}={\frac {y\left(-c+\gamma x\right)}{x\left(a-\alpha y\right)}}$$

Logo:

$${\frac {dy}{dx}}={\frac {y\left(-c+\gamma x\right)}{x\left(a-\alpha y\right)}}$$

$${\frac {\left(a-\alpha y\right)}{y}}dy={\frac {\left(-c+\gamma x\right)}{x}}dx$$

$$\left({\frac {a}{y}}-\alpha \right)dy=\left(-{\frac {c}{x}}+\gamma \right)dx$$

Integrando ambos os lados:

$$a\ln y-\alpha y=-c\ln x+\gamma x+C$$

$$a\ln y-\alpha y+c\ln x-\gamma x=C$$

Onde ${\textstyle C}$ é uma constante de integração. Para plotarmos um gráfico, considerando apenas ${\textstyle a=\alpha =\gamma =c=1}$ Temos então:

$$\ln y+\ln x-\left(x+y\right)=C$$

Um ponto de equilíbrio fora da origem é obtido quando:

$${\frac {dx}{dt}}=x\left(a-\alpha y\right)=0\rightarrow y={\frac {a}{\alpha }}=1$$

$${\frac {dy}{dt}}=y\left(-c+\gamma x\right)=0\rightarrow x={\frac {c}{\gamma }}=1$$

Então neste caso, o sistema oscila em torno de ${\textstyle \left(1,1\right)}$ e a constante ${\textstyle C}$ é definida pelas condições iniciais ${\textstyle \left(x_{0},y_{0}\right)}$. Para a condição em que ${\textstyle x_{0}=y_{0}=1}$, então:

$$\ln 1+\ln 1-\left(1+1\right)=C$$

$$-2=C$$

Então para este conjunto de parâmetros e condições iniciais:

$$\ln y+\ln x-\left(x+y\right)+2=0$$

Neste caso o sistema vai permanecer no ponto de equilíbrio. Para outras condições iniciais, o sistema vai oscilar em torno do ponto de equilíbrio. Obviamente além do ponto ${\textstyle \left(1,1\right)}$, temos um ponto de equilíbrio em ${\textstyle \left(0,0\right)}$. Vamos analisar a dinâmica na vizinhança dos pontos através de um processo simples de linearização.

$f\left(x,y\right)=\ln y+\ln x-\left(x+y\right)-C$ com as condições $a=\alpha =c=\gamma =1$ e condição inicial arbitrária, plotado no GeoGebra.

Linearização em torno do ponto de equilíbrio

Primeiro podemos perceber que o sistema é quase-linear em torno de ${\textstyle \left(0,0\right)}$, verificando que satisfaz:

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}\left[{\frac {\text{parte não linear}}{\text{parte linear}}}\right]=0$$

Então lembrando as equações:

• ${\textstyle {\frac {dx}{dt}}=\left[xa\right]-\left(\alpha xy\right)=\left[{\text{linear}}\right]-\left({\text{não linear}}\right)}$
• ${\textstyle {\frac {dy}{dt}}=-\left[yc\right]+\left(\gamma yx\right)=-\left[{\text{linear}}\right]+\left({\text{não linear}}\right)}$

Logo:

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\alpha xy}{xa}}=\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\alpha }{a}}y=0$$

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\gamma xy}{cy}}=\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\gamma }{c}}x=0$$

Desprezando então os termos não lineares podemos escrever o seguinte sistema linearizado em torno da origem:

$$\left({\begin{array}{c}{\dot {x}}\\{\dot {y}}\end{array}}\right)=\left({\begin{array}{cc}a&0\\0&-c\end{array}}\right)\left({\begin{array}{c}x\\y\end{array}}\right)$$

Calculando os autovalores da matriz, obtemos então:

$$-\left(a-\lambda \right)\left(-c-\lambda \right)=0$$

$$\left(a-\lambda \right)\left(c+\lambda \right)=0$$

os seguintes autovalores ${\textstyle \lambda =\left\{a,-c\right\}}$. Como um dos valores tem parte real positiva, então é um ponto instável, especificamente devido aos sinais opostos é um ponto de sela. Como é instável significa que se a condição inicial for próxima de ${\textstyle \left(0,0\right)}$, a evolução do sistema vai se afastar do ponto de equilíbrio. Essa aproximação também indica que próximo do ponto de equilíbrio, a dinâmica pode ser descrita tanto pelo conjunto de equações não lineares, como pelo sistema linear.

Agora o segundo ponto de equilíbrio, de maneira geral é ${\textstyle \left({\frac {c}{\gamma }},{\frac {a}{\alpha }}\right)}$. Primeiro reescrevemos o sistema em torno do ponto de equilíbrio, isto é, fazemos um deslocamento ${\textstyle u=x-{\frac {c}{\gamma }}}$ e ${\textstyle v=y-{\frac {a}{\alpha }}}$. Então temos ${\textstyle dx=du}$ e ${\textstyle dv=dy}$ e substituindo, para ${\textstyle {\dot {x}}}$:

$${\frac {du}{dt}}=\left(u+{\frac {c}{\gamma }}\right)a-\alpha \left(u+{\frac {c}{\gamma }}\right)\left(v+{\frac {a}{\alpha }}\right)$$

$${\frac {du}{dt}}=ua+{\frac {c}{\gamma }}a-\alpha uv-{\frac {\alpha c}{\gamma }}v-ua-{\frac {ca}{\gamma }}$$

$${\frac {du}{dt}}=-\alpha uv-{\frac {\alpha c}{\gamma }}v$$

E para ${\textstyle {\dot {y}}}$:

$${\frac {dv}{dt}}=-\left(v+{\frac {a}{\alpha }}\right)c+\gamma \left(v+{\frac {a}{\alpha }}\right)\left(u+{\frac {c}{\gamma }}\right)$$

$${\frac {dv}{dt}}=-cv-{\frac {ca}{\alpha }}+\gamma vu+{\frac {\gamma a}{\alpha }}u+cv+{\frac {ca}{\alpha }}$$

$${\frac {dv}{dt}}=\gamma vu+{\frac {\gamma a}{\alpha }}u$$

Podemos analisar o comportamento em torno do ponto de equilíbrio:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}-{\frac {\alpha uv}{\frac {\alpha vc}{\gamma }}}=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}-{\frac {\gamma }{c}}u=0$$

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma vu}{\frac {\gamma au}{\alpha }}}=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\alpha }{a}}v=0$$

Desprezando os termos não lineares então:

$$\left({\begin{array}{c}{\dot {u}}\\{\dot {v}}\end{array}}\right)=\left({\begin{array}{cc}0&-{\frac {\alpha c}{\gamma }}\\{\frac {\gamma a}{\alpha }}&0\end{array}}\right)\left({\begin{array}{c}u\\v\end{array}}\right)$$

Então os autovalores correspondentes:

$$-\lambda ^{2}-{\frac {\gamma a}{\alpha }}{\frac {\alpha c}{\gamma }}=0$$

$$\lambda =\pm {\sqrt {-ac}}=\pm {\sqrt {ac}}i$$

Como temos raízes puramente imaginárias e ${\textstyle \lambda _{1}=\lambda _{2}^{*}}$, temos um centro, ponto de estabilidade. Isto é, se a condição inicial for próxima de ${\textstyle \left({\frac {c}{\gamma }},{\frac {a}{\alpha }}\right)}$ o sistema evoluirá de forma que o estado do sistema permanecerá próximo do ponto de equilíbrio.

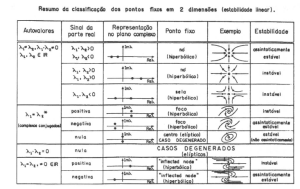
Classificação dos pontos de estabilidade de acordo com os autovalores.alt=

Segundo método de Lyapunov

Para avaliar o ponto ${\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}$, podemos usar de maneira análoga ao exemplo do segundo critério de Lyapunov:

$$V\left({\boldsymbol {x}}\right)={\frac {x^{2}}{\alpha }}-{\frac {y^{2}}{\gamma }}$$

Como já discutimos ${\textstyle V\left({\boldsymbol {x}}_{0}\right)=0}$ e a região ${\textstyle W^{+}\left\{\left(x,y\right)|\left|x\right|>\left|y\right|\right\}}$ onde ${\textstyle V\left({\boldsymbol {x}}\right)>0}$ para ${\textstyle {\boldsymbol {x}}\neq {\boldsymbol {x}}_{0}}$ , sendo ${\textstyle {\boldsymbol {x}}_{0}}$ um ponto de acumulação em ${\textstyle W^{+}}$. Então:

$${\begin{aligned}{\dot {V}}\left({\boldsymbol {x}}\right)&=\left[\nabla V\right]\cdot \left[{\boldsymbol {f}}\left({\boldsymbol {x}}\right)\right]\\&=\left({\frac {2x}{\alpha }},-{\frac {2y}{\gamma }}\right)\left({\dot {x}},{\dot {y}}\right)\\&=2x^{2}{\frac {a}{\alpha }}-2x^{2}y+2y^{2}{\frac {c}{\gamma }}-2y^{2}x\\&=2x^{2}\left({\frac {a}{\alpha }}-y\right)+2y^{2}\left({\frac {c}{\gamma }}-x\right)\end{aligned}}$$

Lembrando do nosso segundo ponto de equilíbrio ${\textstyle \left(x_{2},y_{2}\right)=\left({\frac {c}{\gamma }},{\frac {a}{\alpha }}\right)}$:

$${\dot {V}}\left({\boldsymbol {x}}\right)=2x^{2}\left(y_{2}-y\right)+2y^{2}\left(x_{2}-x\right)$$

Então se estamos próximos suficiente do ponto de equilíbrio em análise ${\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}$, temos então uma instabilidade local pois ${\textstyle {\dot {V}}\left({\boldsymbol {x}}\right)>0}$ é positivo definido em ${\textstyle W^{+}}$, uma vez que ${\textstyle \left|y\right|<\left|y_{2}\right|}$ , ${\textstyle \left|x\right|<\left|x_{2}\right|}$. Olhando o segundo ponto de equilíbrio, ${\textstyle \left(x_{2},y_{2}\right)=\left({\frac {c}{\gamma }},{\frac {a}{\alpha }}\right)}$, podemos manipular as equações da seguinte forma:

• ${\textstyle {\frac {dx}{dt}}=x\left(a-\alpha y\right)=x\alpha \left({\frac {a}{\alpha }}-y\right)=x\alpha \left(y_{2}-y\right)}$
• ${\textstyle {\frac {dy}{dt}}=y\left(-c+\gamma x\right)=y\gamma \left(-{\frac {c}{\gamma }}+x\right)=y\gamma \left(-x_{2}+x\right)}$

Definindo então a seguinte função de Lyapunov:

$$V\left(x,y\right)=x-x_{2}\left[1+\ln \left({\frac {x}{x_{2}}}\right)\right]+{\frac {\alpha }{\gamma }}\left(y-y_{2}\left[1+\ln \left({\frac {y}{y_{2}}}\right)\right]\right)$$

Analisando no ponto de e equilíbrio, temos:

$${\begin{aligned}V\left(x_{2},y_{2}\right)&=x_{2}-x_{2}\left[1+\ln \left({\frac {x_{2}}{x_{2}}}\right)\right]+{\frac {\alpha }{\gamma }}\left(y_{2}-y_{2}\left[1+\ln \left({\frac {y_{2}}{y_{2}}}\right)\right]\right)\\&=x_{2}-x_{2}+{\frac {\alpha }{\gamma }}\left(y_{2}-y_{2}\right)\\&=0\end{aligned}}$$

Agora precisamos que para ${\textstyle \left(x,y\right)\neq 0}$ tenhamos ${\textstyle V>0}$, na região próxima ao ponto de equilíbrio. Separando em dois termos:

$${\begin{aligned}V\left(x,y\right)&=\left[x-x_{2}\left(1+\ln \left({\frac {x}{x_{2}}}\right)\right)\right]+{\frac {\alpha }{\gamma }}\left[y-y_{2}\left(1+\ln \left({\frac {y}{y_{2}}}\right)\right)\right]\\&=V\left(x\right)+{\frac {\alpha }{\gamma }}V\left(y\right)\end{aligned}}$$

De forma geral temos ${\textstyle V\left(z\right)=z-z_{2}\left(1+\ln \left({\frac {z}{z_{2}}}\right)\right)}$, e precisamos que ${\textstyle V\left(z\right)>0}$ quando ${\textstyle z\neq z_{2}}$. Além de ser facilmente visto via gráfico para todos os valores aceitáveis ${\textstyle z,z_{2}\in \left[0,1\right]}$, também podemos analisar a seguinte desigualdade:

$${\begin{aligned}z-z_{2}\left(1+\ln \left({\frac {z}{z_{2}}}\right)\right)&>0\\z&>z_{2}\left(1+\ln \left({\frac {z}{z_{2}}}\right)\right)\\{\frac {z}{z_{2}}}&>1+\ln \left({\frac {z}{z_{2}}}\right)\\e^{\frac {z}{z_{2}}}&>e{\frac {z}{z_{2}}}\\e^{u}&>eu\end{aligned}}$$

Podemos ver quer a desigualdade desigualdade é válida exceto se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x=1} . Mas como fizemos a seguinte substituição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=\frac{z}{z_{2}}} então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=1\rightarrow z=z_{2}} , e de fato que queremos que seja positiva definida fora do ponto de equilíbrio. Uma vez que sabemos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(x,y\right)} é positivo definido, calculamos então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{V}\left(\boldsymbol{x}\right) & =\left[\nabla V\right]\cdot\left[\boldsymbol{f}\left(\boldsymbol{x}\right)\right]\\ & =\left[\frac{\partial V\left(x\right)}{\partial x},\frac{\alpha}{\gamma}\frac{\partial V\left(y\right)}{\partial y}\right]\cdot\left[x\alpha\left(y_{2}-y\right),y\gamma\left(-x_{2}+x\right)\right] \\ & =\left[1-\frac{x_{2}}{x},\frac{\alpha}{\gamma}\left(1-\frac{y_{2}}{y}\right)\right]\cdot\left[x\alpha\left(y_{2}-y\right),y\gamma\left(-x_{2}+x\right)\right]\\ & =\left(\frac{x-x_{2}}{x}\right)\left(x\alpha\left(y_{2}-y\right)\right)+\frac{\alpha}{\gamma}\left(\frac{y-y_{2}}{y}\right)\left(y\gamma\left(-x_{2}+x\right)\right)\end{align}}

Então:Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{V}\left(\boldsymbol{x}\right)=\alpha\left(x-x_{2}\right)\left(y_{2}-y\right)-\alpha\left(y_{2}-y\right)\left(x-x_{2}\right)=0} Temos então a condição de estabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\leq0} concordando como que já havíamos obtidos anteriormente.

Principais materiais utilizados

1. A survey of constructing Lyapunov functions for mathematical models in population biology (Sze-Bi, Revista Taiwanesa de Matemática )
2. Estabilidade de pontos de equilíbrio e existência de soluções periódicas em alguns modelos bidimensionais (Salvador Tavares de Oliveira, UNESP)
3. Modelagem Matemática e estabilidade de sistemas predador-presa (Paulo Laerte Natti e outros, UEL)
4. Modelo de Lotka-Volterra: a dinâmica predador-presa (Rafael Biasi Pata e Elisa Regina Cara, UNIPAMPA)

Citações

Anterior: Métodos de Lyapunov | Índice: Ecologia | Próximo: Modelo de Lotka-Volterra amortecido