Modelo de Lotka-Volterra

De Física Computacional
Ir para navegação Ir para pesquisar

Anterior: Jogo da Vida | Índice: Ecologia | Próximo: Modelo de Lotka-Volterra amortecido

Versão tradicional

No modelo de Lotka-Volterra temos as seguintes considerações:

  • Na ausência de predadores, a população de presas aumenta a uma taxa proporcional à população atual;
  • Na ausência de presas, os predadores irão à extinção;
  • O número de encontro entre presas e predadores é proporcional a produto das duas populações.
    • Estes encontros beneficiam os predadores em detrimento das presas.

Dessa forma, as equações são:

  • Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dx}{dt}=x\left(a-\alpha y\right)}
  • Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dy}{dt}=y\left(-c+\gamma x\right)}

Onde:

  • taxa de crescimento de presas sem predadores;
  • taxa de decréscimo da população de presas devido a predação;
  • taxa de mortalidade da população de predadores sem presas;
  • : taxa de crescimento de predadores devido a predação.

Separação de variáveis

Utilizando a separação de variáveis, temos:

Logo:

Integrando ambos os lados:

Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle C} é uma constante de integração. Para plotarmos um gráfico, considerando apenas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle a=\alpha=\gamma=c=1} Temos então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln y+\ln x-\left(x+y\right)=C}

Um ponto de equilíbrio fora da origem é obtido quando:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=x\left(a-\alpha y\right)=0\rightarrow y=\frac{a}{\alpha}=1} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}=y\left(-c+\gamma x\right)=0\rightarrow x=\frac{c}{\gamma}=1}

Então neste caso, o sistema oscila em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(1,1\right)} e a constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle C} é definida pelas condições iniciais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{0},y_{0}\right)} . Para a condição em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{0}=y_{0}=1} , então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln1+\ln1-\left(1+1\right)=C} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2=C}

Então para este conjunto de parâmetros e condições iniciais: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln y+\ln x-\left(x+y\right)+2=0}

Neste caso o sistema vai permanecer no ponto de equilíbrio. Para outras condições iniciais, o sistema vai oscilar em torno do ponto de equilíbrio. Obviamente além do ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(1,1\right)} , temos um ponto de equilíbrio em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} . Vamos analisar a dinâmica na vizinhança dos pontos através de um processo simples de linearização.

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f\left(x,y\right)=\ln y+\ln x-\left(x+y\right)-C} com as condições Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=\alpha=c=\gamma=1} e condição inicial arbitrária, plotado no GeoGebra.

Linearização em torno do ponto de equilíbrio

Primeiro podemos perceber que o sistema é quase-linear em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} , verificando que satisfaz:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}\left[\frac{\text{parte não linear}}{\text{parte linear}}\right]=0}

Então lembrando as equações:

  • Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dx}{dt}=\left[xa\right]-\left(\alpha xy\right)=\left[\text{linear}\right]-\left(\text{não linear}\right)}
  • Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dy}{dt}=-\left[yc\right]+\left(\gamma yx\right)=-\left[\text{linear}\right]+\left(\text{não linear}\right)}

Logo:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha xy}{xa}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha}{a}y=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma xy}{cy}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}x=0}

Desprezando então os termos não lineares podemos escrever o seguinte sistema linearizado em torno da origem:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} a & 0\\ 0 & -c \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)} Calculando os autovalores da matriz, obtemos então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\left(a-\lambda\right)\left(-c-\lambda\right)=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(a-\lambda\right)\left(c+\lambda\right)=0}


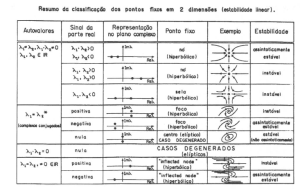
os seguintes autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda=\left\{ a,-c\right\}} . Como um dos valores tem parte real positiva, então é um ponto instável, especificamente devido aos sinais opostos é um ponto de sela. Como é instável significa que se a condição inicial for próxima de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} , a evolução do sistema vai se afastar do ponto de equilíbrio. Essa aproximação também indica que próximo do ponto de equilíbrio, a dinâmica pode ser descrita tanto pelo conjunto de equações não lineares, como pelo sistema linear.

Agora o segundo ponto de equilíbrio, de maneira geral é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{a}{\alpha}\right)} . Primeiro reescrevemos o sistema em torno do ponto de equilíbrio, isto é, fazemos um deslocamento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=x-\frac{c}{\gamma}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v=y-\frac{a}{\alpha}} . Então temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle dx=du} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle dv=dy} e substituindo, para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{x}} :Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left(u+\frac{c}{\gamma}\right)a-\alpha\left(u+\frac{c}{\gamma}\right)\left(v+\frac{a}{\alpha}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=ua+\frac{c}{\gamma}a-\alpha uv-\frac{\alpha c}{\gamma}v-ua-\frac{ca}{\gamma}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=-\alpha uv-\frac{\alpha c}{\gamma}v} E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{y}} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=-\left(v+\frac{a}{\alpha}\right)c+\gamma\left(v+\frac{a}{\alpha}\right)\left(u+\frac{c}{\gamma}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=-cv-\frac{ca}{\alpha}+\gamma vu+\frac{\gamma a}{\alpha}u+cv+\frac{ca}{\alpha}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\gamma vu+\frac{\gamma a}{\alpha}u} Podemos analisar o comportamento em torno do ponto de equilíbrio:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}-\frac{\alpha uv}{\frac{\alpha vc}{\gamma}}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}u=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma vu}{\frac{\gamma au}{\alpha}}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\alpha}{a}v=0} Desprezando os termos não lineares então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} 0 & -\frac{\alpha c}{\gamma}\\ \frac{\gamma a}{\alpha} & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Então os autovalores correspondentes:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\lambda^{2}-\frac{\gamma a}{\alpha}\frac{\alpha c}{\gamma}=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\pm\sqrt{-ac}=\pm\sqrt{ac}i}

Como temos raízes puramente imaginárias e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1}=\lambda_{2}^{*}} , temos um centro, ponto de estabilidade. Isto é, se a condição inicial for próxima de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{a}{\alpha}\right)} o sistema evoluirá de forma que o estado do sistema permanecerá próximo do ponto de equilíbrio.

Classificação dos pontos de estabilidade de acordo com os autovalores[1].

Segundo método de Lyapunov

Para avaliar o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)} , podemos usar de maneira análoga ao exemplo do segundo critério de Lyapunov:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(\boldsymbol{x}\right)=\frac{x^{2}}{\alpha}-\frac{y^{2}}{\gamma}}

Como já discutimos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}_{0}\right)=0} e a região Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}\left\{ \left(x,y\right)|\left|x\right|>\left|y\right|\right\}} onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)>0} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}\neq\boldsymbol{x}_{0}} , sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}_{0}} um ponto de acumulação em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} [2]. Então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{V}\left(\boldsymbol{x}\right) & =\left[\nabla V\right]\cdot\left[\boldsymbol{f}\left(\boldsymbol{x}\right)\right]\\ & =\left(\frac{2x}{\alpha},-\frac{2y}{\gamma}\right)\left(\dot{x},\dot{y}\right)\\ & =2x^{2}\frac{a}{\alpha}-2x^{2}y+2y^{2}\frac{c}{\gamma}-2y^{2}x\\ & =2x^{2}\left(\frac{a}{\alpha}-y\right)+2y^{2}\left(\frac{c}{\gamma}-x\right)\end{align}} Lembrando do nosso segundo ponto de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{2},y_{2}\right)=\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{V}\left(\boldsymbol{x}\right)=2x^{2}\left(y_{2}-y\right)+2y^{2}\left(x_{2}-x\right)}


Então se estamos próximos suficiente do ponto de equilíbrio em análise Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)} , temos então uma instabilidade local pois Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\left(\boldsymbol{x}\right)>0} é positivo definido em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} , uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|y\right|<\left|y_{2}\right|} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|x\right|<\left|x_{2}\right|} . Olhando o segundo ponto de equilíbrio, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{2},y_{2}\right)=\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)} , podemos manipular as equações da seguinte forma:

  • Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dx}{dt}=x\left(a-\alpha y\right)=x\alpha\left(\frac{a}{\alpha}-y\right)=x\alpha\left(y_{2}-y\right)}
  • Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dy}{dt}=y\left(-c+\gamma x\right)=y\gamma\left(-\frac{c}{\gamma}+x\right)=y\gamma\left(-x_{2}+x\right)}

Definindo então a seguinte função de Lyapunov:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(x,y\right)=x-x_{2}\left[1+\ln\left(\frac{x}{x_{2}}\right)\right]+\frac{\alpha}{\gamma}\left(y-y_{2}\left[1+\ln\left(\frac{y}{y_{2}}\right)\right]\right)}

Analisando no ponto de e equilíbrio, temos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} V\left(x_{2},y_{2}\right) & =x_{2}-x_{2}\left[1+\ln\left(\frac{x_{2}}{x_{2}}\right)\right]+\frac{\alpha}{\gamma}\left(y_{2}-y_{2}\left[1+\ln\left(\frac{y_{2}}{y_{2}}\right)\right]\right)\\ & =x_{2}-x_{2}+\frac{\alpha}{\gamma}\left(y_{2}-y_{2}\right)\\ & =0\end{align}}

Agora precisamos que para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x,y\right)\neq0} tenhamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V>0} , na região próxima ao ponto de equilíbrio. Separando em dois termos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} V\left(x,y\right) & =\left[x-x_{2}\left(1+\ln\left(\frac{x}{x_{2}}\right)\right)\right]+\frac{\alpha}{\gamma}\left[y-y_{2}\left(1+\ln\left(\frac{y}{y_{2}}\right)\right)\right]\\ & =V\left(x\right)+\frac{\alpha}{\gamma}V\left(y\right)\end{align}}

De forma geral temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(z\right)=z-z_{2}\left(1+\ln\left(\frac{z}{z_{2}}\right)\right)} , e precisamos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(z\right)>0} quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle z\neq z_{2}} . Além de ser facilmente visto via gráfico para todos os valores aceitáveis Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle z,z_{2}\in\left[0,1\right]} , também podemos analisar a seguinte desigualdade:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} z-z_{2}\left(1+\ln\left(\frac{z}{z_{2}}\right)\right) & >0\\ z & >z_{2}\left(1+\ln\left(\frac{z}{z_{2}}\right)\right)\\ \frac{z}{z_{2}} & >1+\ln\left(\frac{z}{z_{2}}\right)\\ e^{\frac{z}{z_{2}}} & >e\frac{z}{z_{2}}\\ e^{u} & >eu\end{align}} Podemos ver quer a desigualdade desigualdade é válida exceto se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x=1} . Mas como fizemos a seguinte substituição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=\frac{z}{z_{2}}} então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=1\rightarrow z=z_{2}} , e de fato que queremos que seja positiva definida fora do ponto de equilíbrio. Uma vez que sabemos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(x,y\right)} é positivo definido, calculamos então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{V}\left(\boldsymbol{x}\right) & =\left[\nabla V\right]\cdot\left[\boldsymbol{f}\left(\boldsymbol{x}\right)\right]\\ & =\left[\frac{\partial V\left(x\right)}{\partial x},\frac{\alpha}{\gamma}\frac{\partial V\left(y\right)}{\partial y}\right]\cdot\left[x\alpha\left(y_{2}-y\right),y\gamma\left(-x_{2}+x\right)\right] \\ & =\left[1-\frac{x_{2}}{x},\frac{\alpha}{\gamma}\left(1-\frac{y_{2}}{y}\right)\right]\cdot\left[x\alpha\left(y_{2}-y\right),y\gamma\left(-x_{2}+x\right)\right]\\ & =\left(\frac{x-x_{2}}{x}\right)\left(x\alpha\left(y_{2}-y\right)\right)+\frac{\alpha}{\gamma}\left(\frac{y-y_{2}}{y}\right)\left(y\gamma\left(-x_{2}+x\right)\right)\end{align}}

Então:Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{V}\left(\boldsymbol{x}\right)=\alpha\left(x-x_{2}\right)\left(y_{2}-y\right)-\alpha\left(y_{2}-y\right)\left(x-x_{2}\right)=0} Temos então a condição de estabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\leq0} concordando como que já havíamos obtidos anteriormente.

Solução numérica

Um exemplo resolvido numericamente pode ser visto em Modelo de Lotka-Volterra amortecido, onde foi aproveitado os códigos desenvolvidos para este mesmo.

Versão adimensional

Originalmente temos 4 parâmetros, mas podemos realizar uma série de manipulações visando uma redução da quantidade de parâmetros. Escrevendo o sistema como:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dN}{dt} & =aN-bNP\\ \frac{dP}{dt} & =cPN-dP \end{align}}

Podemos definir então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \widehat{t}=at} . Multiplicando ambas equações por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 1/a} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{a}\frac{dN}{dt} & =N-\frac{b}{a}NP\\ \frac{1}{a}\frac{dP}{dt} & =\frac{c}{a}PN-\frac{d}{a}P \end{align}}

Se definimos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle p=\left(b/a\right)P} e multiplicamos a segunda equação por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle b/a} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dN}{d\widehat{t}} & =N-Np\\ \frac{d}{d\widehat{t}}\left(\frac{bP}{a}\right) & =\frac{c}{a}\left(\frac{b}{a}P\right)N-\frac{d}{a}\left(\frac{b}{a}P\right) \end{align}}

Agora se multiplicamos a primeira linha e definimos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle n=\left(c/d\right)N} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{d}{d\widehat{t}}\left(\frac{c}{d}N\right) & =\frac{c}{d}N-\left(\frac{c}{d}N\right)p\\ \frac{dp}{d\widehat{t}} & =\frac{c}{a}pN-\frac{d}{a}p \end{align}}

Definindo então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha=\frac{d}{a}} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{d n}{d\widehat{t}} & =n-np\\ \frac{dp}{d\widehat{t}} & =\frac{c}{a}\frac{d}{c}pn-\alpha p \end{align}}

Ou então, ficamos apenas com um único parâmetro.

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dn}{d\widehat{t}} & =n\left(1-p\right)\\ \frac{dp}{d\widehat{t}} & =\alpha p\left(n-1\right) \end{align}}

Separação de variáveis

Aplicando a separação de variáveis, temos então: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dp}{dn} & =\frac{\alpha p\left(n-1\right)}{n\left(1-p\right)}\\ \frac{\left(1-p\right)}{p}dp & =\alpha\frac{\left(n-1\right)}{n}dn\\ \left(\frac{1}{p}-1\right)dp & =\alpha\left(1-\frac{1}{n}\right)dn\\ \ln p-p+K & =\alpha\left(n-\ln\left(n\right)\right)\\ K & =\alpha n+p-\alpha\ln\left(n\right)-\ln p \end{align}}

Ou ainda, apenas:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=\alpha n+p+\ln\left(n^{\alpha}p\right)}

Referências

Principais materiais utilizados

  1. A survey of constructing Lyapunov functions for mathematical models in population biology (Sze-Bi, Revista Taiwanesa de Matemática )
  2. Estabilidade de pontos de equilíbrio e existência de soluções periódicas em alguns modelos bidimensionais (Salvador Tavares de Oliveira, UNESP)
  3. Modelagem Matemática e estabilidade de sistemas predador-presa (Paulo Laerte Natti e outros, UEL)
  4. Modelo de Lotka-Volterra: a dinâmica predador-presa (Rafael Biasi Pata e Elisa Regina Cara, UNIPAMPA)

Citações

  1. ↑ Análise de sistemas não-lineares (Vilma A. Oliveira e José Ricardo Rosolen, USP)
  2. ↑ Stability Analysis of Nonlinear Systems (Roberto Zanasi, Universidade de Módena e Reggio Emília)

Anterior: Jogo da Vida | Índice: Ecologia | Próximo: Modelo de Lotka-Volterra amortecido

Disponível em “http://fiscomp.if.ufrgs.br/index.php?title=Modelo_de_Lotka-Volterra&oldid=9183”