Grupo3 - Ondas2: mudanças entre as edições
| (137 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo: Lucas Dória, Caetano Pires e Ânderson Rosa.''' | |||
O objetivo deste trabalho é analisar três métodos diferentes de integração numérica para resolução de equações diferenciais parciais (EDP's). A equação aqui abordada é a equação da onda, a qual consiste em uma EDP hiperbólica de segunda ordem. Uma pequena noção dos métodos numéricos é dada, após a explicação do problema físico abordado. Os dados encontrados são comentados e comparados com os resultados esperados. Simulações também foram feitas para melhor visualização dos fenômenos. Por último, foi feita uma análise de erros e estabilidade para cada um dos métodos, assim como algumas conclusões foram inferidas. | |||
== Introdução == | == Introdução == | ||
Equações diferenciais parciais | Equações diferenciais parciais hiperbólicas geralmente podem ser formuladas a partir de teoremas de conservação. Um exemplo é a equação do tipo: | ||
<math>\frac{\partial \vec{U}}{\partial t} + \nabla \cdot \vec{F}(U) = \vec{S}(U)</math> | <math>\frac{\partial \vec{U}}{\partial t} + \nabla \cdot \vec{F}(U) = \vec{S}(U),</math> | ||
onde <math>\vec{U}</math> é o vetor de densidades da quantidade conservada, i.e., <math>\vec{U} = (U_1,...,U_n)</math> | onde <math>\vec{U}</math> é o vetor de densidades da quantidade conservada, i.e., <math>\vec{U} = (U_1,...,U_n),</math> <math>\vec{F}</math> é o fluxo de densidade e <math>\vec{S}</math> é um termo genérico representando fontes e/ou sumidouros. | ||
Uma classe especial de equações hiperbólicas são as chamadas equações de adveção, na qual a derivada temporal da quantidade conservada <math>\vec{U}(\vec{x},t)</math> é proporcional à sua derivada espacial. Nesses casos, <math>\vec{F}(U)</math> é diagonal e dada por: | Uma classe especial de equações hiperbólicas são as chamadas equações de adveção, na qual a derivada temporal da quantidade conservada <math>\vec{U}(\vec{x},t)</math> é proporcional à sua derivada espacial. Nesses casos, <math>\vec{F}(U)</math> é diagonal e dada por: | ||
<math>\vec{F}(U) = v | <math>\vec{F}(U) = v I \cdot \vec{U},</math> | ||
onde <math> | onde <math>I</math> é a matriz identidade. | ||
Considerando apenas uma dimensão e com <math>\vec{U} \equiv u</math>, temos a equação de adveção: | Considerando apenas uma dimensão e com <math>\vec{U} \equiv u</math>, temos a equação de adveção: | ||
<math>\frac{\partial u}{\partial t} + v \frac{\partial u}{\partial x} = 0</math> | <math>\frac{\partial u}{\partial t} + v \frac{\partial u}{\partial x} = 0,</math> | ||
onde <math>v</math> é a velocidade de propagação do pulso gerado. A equação admite uma solução analítica da forma <math>u = f(x - vt)</math> | onde <math>v</math> é a velocidade de propagação do pulso gerado. A equação admite uma solução analítica da forma <math>u = f(x - vt),</math> representando um pulso se movendo na direção positiva de <math>x.</math> | ||
A equação da onda em uma dimensão é uma EDP hiperbólica de segunda ordem dada por | A equação da onda em uma dimensão é uma EDP hiperbólica de segunda ordem dada por | ||
<math> | <math> | ||
\frac{\ | \frac{\partial^2 u}{\partial t^2} = v^2 \frac{\partial^2 u}{\partial x^2}, | ||
</math> | </math> | ||
onde <math>u = u(x,t)</math> é o deslocamento transversal à direção de propagação de uma posição <math>x</math> no instante <math>t</math> e admite duas soluções, representadas por pulsos, na forma <math>f_1(x + vt)</math> e <math>f_2(x - vt).</math> | |||
Assumindo que <math>v | Assumindo que <math>v</math> não depende da posição na equação da onda, nos restringimos a problemas lineares. Além disso, se escrevermos | ||
<math> | <math> | ||
k = v \frac{\partial u}{\partial x} | k = v \frac{\partial u}{\partial x},\qquad s = \frac{\partial u}{\partial t}, | ||
</math> | </math> | ||
| Linha 36: | Linha 40: | ||
<math> | <math> | ||
\begin{cases}\frac{\partial k}{\partial t} = v\frac{\partial s}{\partial x} \\ | \begin{cases}\displaystyle \frac{\partial k}{\partial t} = v\frac{\partial s}{\partial x} \\\\ | ||
\frac{\partial s}{\partial t} = v\frac{\partial k}{\partial x} \\ | \displaystyle \frac{\partial s}{\partial t} = v\frac{\partial k}{\partial x} \\\\ | ||
\frac{\partial u}{\partial t} = s | \displaystyle \frac{\partial u}{\partial t} = s | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
Em notação vetorial, o sistema acima pode ser reescrito na forma conservativa como: <math>\frac{\partial U}{\partial t}+ \frac{\partial F(U)}{\partial x} = 0 </math> | Em notação vetorial, o sistema acima pode ser reescrito na forma conservativa como: <math>\frac{\partial U}{\partial t}+ \frac{\partial F(U)}{\partial x} = 0, </math> | ||
onde <math>U = \begin{pmatrix}k\\s\end{pmatrix},\quad \textrm{e}\quad F(U) =\begin{pmatrix}0 & -v\\-v & 0\end{pmatrix}</math> | onde <math>U = \begin{pmatrix}k\\s\end{pmatrix},\quad \textrm{e}\quad F(U) =\begin{pmatrix}0 & -v\\-v & 0\end{pmatrix}</math> | ||
== | ==Condição CFL== | ||
Uma condição necessária mas nem sempre suficiente para a convergência de equações diferenciais parciais resolvidas a partir de métodos de diferença, conhecida como condição CFL <ref>Luciano Rezzolla, "Numerical Methods for the Solution of Partial Differential Equations". Albert Einstein Institute, Max-Planck-Institute for Gravitational Physics, Potsdam, Germany.</ref>, é formulada a partir do termo de “domínio de dependência”. | |||
Considerando, por exemplo, a equação da advecção [https://en.wikipedia.org/wiki/Advection] em uma aproximação a partir de métodos de diferença em sua forma explícita | |||
<math>\frac{U^{n+1}_i-U^n_i}{\Delta t} + v\frac{U^n_{i}-U^n_{i-1}}{\Delta x}=0,</math> | |||
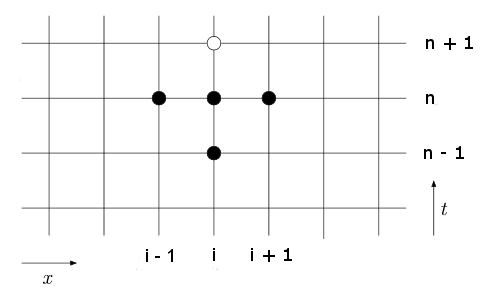
diz-se que o valor de <math>U^{n+1}_i</math> depende dos valores anteriores de <math>U^n_i</math> e <math>U^n_{i-1}</math>, e esses dois pontos dependem, novamente, de outros dois pontos em tempos anteriores. Todos esses pontos dependentes formam o domínio de dependência do valor <math>U^{n+1}_i</math>, representado abaixo (botar figura do domínio de dependência). | |||
A condição CFL enuncia que a condição mínima para que haja estabilidade em métodos de diferenças o domínio de dependência da equação diferencia parcial, dado por sua equação característica, deve estar situado dentro do domínio de dependência do esquema numérico. | |||
A partir dessa condição, define-se o número CFL como | |||
<math>u(i,n+1 | <math>r\equiv v\frac{\Delta t}{\Delta x}</math> | ||
onde <math>\Delta t</math> é um passo na malha temporal e <math>\Delta x</math> é um passo na malha espacial. Para casos unidimensionais, como o que será tratado aqui, a condição CFL é satisfeita se r | |||
<math> \left|r\right| \le 1 </math> | |||
Um uso da condição CFL é determinar o tamanho do passo temporal, sabendo-se <math>v</math> e <math>\Delta x</math>: | |||
<math>\Delta t = c_{cfl}\frac{\Delta x}{\left|v\right|}</math> | |||
onde o fator <math>c_{cfl}<1</math>. | |||
O número CFL pode ser entendido como um fluxo numérico advectivo adimensionalisado pelas malhas espacial e temporal do problema. De um ponto de vista matemático, ele garante que o domínio numérico de dependência é sempre maior que o domínio físico. De um ponto de vista físico, é garantido que a velocidade de propagação de qualquer perturbação, como uma onda, seja menor ou ao menos igual que a velocidade de propagação numérica, fazendo com que a distância propagada pela perturbação não seja maior do que a divisão da malha espacial: | |||
<math>\left|v\right|\Delta t \le \Delta x </math> | |||
== O Problema Físico == | |||
===O Modelo de Corda Ideal=== | |||
Para uma primeira abordagem da equação da onda, consideramos uma corda com suas extremidades fixas. Podemos dividir o comprimento <math>L</math> dessa corda em <math>K</math> intervalos de comprimentos iguais, dessa forma <math>\Delta x = \frac{L}{K}</math>. Cada intervalo é discretizado, representado por <math>x_i</math>, <math>i=0,1,...,K</math>. Também podemos dividir o tempo em intervalos iguais <math>\Delta t</math> e denotá-los como <math>t_n</math>, <math>n =0,1,...,t_{max}</math>. Abaixo temos uma esquematização das informações que precisamos para cada ponto da corda: | |||
[[Arquivo:grid.png]] | |||
Tendo feita a discretização das variáveis, podemos aproximar a equação da onda por diferenciação finita, utilizando derivadas centradas da seguinte forma: | |||
<math>\frac{\partial^2u}{\partial t^2}=\frac{U^{n+1}_{i}-2U^n_i+U^{n-1}_i}{\Delta t^2}</math> | |||
<math>\frac{\partial^2u}{\partial x^2}=\frac{U^{n}_{i+1}-2U^n_i+U^{n}_{i-1}}{\Delta x^2}</math> | |||
onde <math>U_i^n</math> representa o valor discretizado de <math>u(x_i,t_n)</math>. | |||
Assim, chegamos em uma equação discretizada: | |||
<math>\frac{U_i^{n+1}-2U_i^n+U_i^{n-1}}{(\Delta t)^2} = v^2 \frac{U_{i+1}^n-2U_i^n+U_{i-1}^n}{(\Delta x)^2}</math>. | |||
Sabendo que essa discretização da equação da onda pode ser verificada como sendo o método Leapfrog (ver seção do método de Leapfrog [https://fiscomp.if.ufrgs.br/index.php/Grupo3_-_Ondas2#O_M.C3.A9todo_de_Leapfrog método de Leapfrog]), podemos resolver a equação para <math>U_i^{n+1}</math> para sabermos o deslocamento vertical de uma partição da corda no momento de tempo seguinte, assim obtendo | |||
<math>U_i^{n+1} = 2(1-r^2)U_i^n + r^2[U_{i+1}^n+U_{i-1}^n]-U_i^{n-1}</math>, | |||
onde <math>r = v \frac{\Delta t}{\Delta x}.</math> | onde <math>r = v \frac{\Delta t}{\Delta x}.</math> | ||
===Um Quadro Mais Realístico=== | ===Um Quadro Mais Realístico - O Modelo de Corda Rígida === | ||
Para nos aproximarmos de um modelo mais real, podemos adicionar um termo à equação original da onda que corresponde ao efeito de fricção em uma corda. | Para nos aproximarmos de um modelo mais real, podemos adicionar um termo à equação original da onda que corresponde ao efeito de fricção em uma corda. A equação da onda mais geral com efeito de fricção pode ser escrita como: <ref name=giordano>N. J. Giordano, "Computational Physics". Department of Physics, Purdue University. Upper Saddle River, New Jersey. Prentice-Hall, 1997.</ref> | ||
<math>\frac{\ | <math>\frac{\partial^2 u}{\partial t^2} = v^2 \left( \frac{\partial^2 u}{\partial x^2} - \epsilon L^2 \frac{\partial^4 u}{\partial x^4} \right),</math> | ||
onde <math>v</math> é a velocidade transversal de propagação do pulso na corda, dada pela relação <math>v = \sqrt[]{\frac{T}{\rho}}</math> (sendo <math>T</math> a tensão na corda e <math>\rho</math> a densidade linear da mesma), <math>\epsilon</math> é um parâmetro adimensional de fricção que representa a rigidez da corda e <math>L</math> o comprimento da corda. | onde <math>v</math> é a velocidade transversal de propagação do pulso na corda, dada pela relação <math>v = \sqrt[]{\frac{T}{\rho}}</math> (sendo <math>T</math> a tensão na corda e <math>\rho</math> a densidade linear da mesma), <math>\epsilon</math> é um parâmetro adimensional de fricção que representa a rigidez da corda e <math>L</math> o comprimento da corda. | ||
| Linha 72: | Linha 116: | ||
O parâmetro <math>\epsilon</math> é dado por | O parâmetro <math>\epsilon</math> é dado por | ||
<math>\epsilon = \kappa² \frac{E S}{T | <math>\epsilon = \kappa² \frac{E S}{T L^2}</math>, | ||
onde <math>\kappa</math> é o raio da corda, <math>E</math> é o Módulo de Young e <math>S</math> a área da secção da corda. | onde <math>\kappa</math> é o [https://en.wikipedia.org/wiki/Radius_of_gyration raio de giro] da corda, <math>E</math> é o [https://en.wikipedia.org/wiki/Young%27s_modulus Módulo de Young] e <math>S</math> a área da secção da corda. | ||
Discretizamos a equação da seguinte maneira: | |||
<math> | <math> | ||
\frac{\partial^2u}{\partial t^2}=\frac{U^{n+1}_{i}-2U^n_i+U^{n-1}_i}{\Delta t^2}</math> | |||
O fato de essa discretização depender do deslocamento da corda em posições <math>i-2</math> e <math>i+2</math> implica em precisarmos simular "pontos fantasmas" quando integramos os extremos das cordas. Para fazermos isso, podemos ou utilizar a aproximação <math> | <math> \frac{\partial^2u}{\partial x^2}=\frac{U^{n}_{i+1}-2U^n_i+U^{n}_{i-1}}{\Delta x^2}</math> | ||
<math> \frac{\partial^4u}{\partial x^4}=\frac{U^n_{i+2}-4U^n_{i+1}+6U^n_i-4U^n_{i-1}+U^n_{i-2}}{\Delta x^4} | |||
</math> | |||
e resolvemos para <math>U_i^{n+1}</math>, obtendo: | |||
<math> U_i^{n+1}=[2-2r^2-6\epsilon r^2K^2]U_i^n - U_i^{n-1} +r^2[1+4\epsilon K^2][U_{i+1}^n+U_{i-1}^n]-\epsilon r^2K^2[U_{i+2}^n + U_{i-2}^n].</math> | |||
O fato de essa discretização depender do deslocamento da corda em posições <math>i-2</math> e <math>i+2</math> implica em precisarmos simular "pontos fantasmas" quando integramos os extremos das cordas. Para fazermos isso, podemos ou utilizar a aproximação <math>U_{-1}^n = -U_{+1}^n</math> ou podemos considerar esses "pontos fantasmas" como pontos presos e, portanto, sempre iguais a zero. | |||
== Os Métodos Utilizados == | == Os Métodos Utilizados == | ||
Foi realizada uma abordagem ao problema da corda real a partir de três métodos diferentes de integração numérica | Foi realizada uma abordagem ao problema da corda real a partir de três métodos diferentes de integração numérica. | ||
O método mais básico é chamado de FTCS (Forward-Time-Centered-Space) e consiste em duas expansões de Taylor ao redor do ponto <math>x_j</math>: | O método mais básico é chamado de FTCS (Forward-Time-Centered-Space) e consiste em duas expansões de Taylor ao redor do ponto <math>x_j</math>: | ||
<math>u( | <math>u(x_i + \Delta x,t^n) = u(x_i,t^n) + \frac{\partial u}{\partial x}(x_i,t^n)\Delta x + \frac{1}{2} \frac{\partial^2 u}{\partial x^2}(x_i,t^n)\Delta x^2 + \mathcal{O}(\Delta x^3),</math> | ||
<math>u( | <math>u(x_i - \Delta x,t^n) = u(x_i,t^n) - \frac{\partial u}{\partial x}(x_i,t^n)\Delta x + \frac{1}{2} \frac{\partial^2 u}{\partial x^2}(x_i,t^n)\Delta x^2 + \mathcal{O}(\Delta x^3).</math> | ||
Subtraindo as duas expressões, encontramos a expressão | Subtraindo as duas expressões, encontramos a expressão | ||
<math>\frac{\partial u}{\partial x} | | <math>\left.\frac{\partial u}{\partial x}\right|_i^n = \frac{u^n_{i+1} - u^n_{i-1}}{2 \Delta x} + \mathcal{O}(\Delta x^2)</math>, | ||
A qual podemos substituir na equação da onda, juntamente com a discretização da derivada parcial temporal. Temos então que, para um sistema linear de equações hiperbólicas: | A qual podemos substituir na equação da onda, juntamente com a discretização da derivada parcial temporal. Temos então que, para um sistema linear de equações hiperbólicas: | ||
<math>\textbf{U}^{n+1} | <math>\textbf{U}^{n+1}_i = \textbf{U}^n_i - \frac{\Delta t}{2 \Delta x} [\textbf{F}^n_{i+1} - \textbf{F}^n_{i-1}] + \mathcal{O}(\Delta t^2, \Delta x^2 \Delta t)</math> | ||
Visto que essa última notação é mais genérica, ela será utilizada para a explicação dos métodos posteriores. | Visto que essa última notação é mais genérica, ela será utilizada para a explicação dos métodos posteriores. | ||
| Linha 104: | Linha 158: | ||
=== O Método de Lax-Friedrichs === | === O Método de Lax-Friedrichs === | ||
O método de Lax-Friedrichs consiste em substituir o termo <math>\textbf{U}^ | O método de Lax-Friedrichs consiste em substituir o termo <math>\textbf{U}^n_i</math> com sua respectiva média espacial, i.e., <math>U^n_i = (U^n_{i+1} + U^n_{i-1})/2</math>. Logo, temos a seguinte equação de recorrência: | ||
<math>\textbf{U}^{n+1} | <math>\textbf{U}^{n+1}_i = \frac{1}{2}(\textbf{U}^n_{i+1} + \textbf{U}^n_{i-1}) - \frac{\Delta t}{2 \Delta x} [\textbf{F}^n_{i+1} - \textbf{F}^n_{i-1}] + \mathcal{O}(\Delta x^2)</math> | ||
=== O Método de Leapfrog === | === O Método de Leapfrog === | ||
Tanto o método FTCS quanto o método de Lax-Friedrichs são métodos de primeira ordem para a derivada temporal. Nessas circunstâncias, <math>v \Delta t</math> deve ser significantemente menor do que <math>\Delta x</math>, muito abaixo do limite imposto pela condição de Courant. | |||
Uma nova expressão para a derivada temporal, com precisão de segunda ordem é dada por | |||
<math>\left.\frac{\partial u}{\partial t}\right|^n_i = \frac{U^{n+1}_i - U^{n-1}_i}{2 \Delta t} + \mathcal{O}(\Delta t^2).</math> | |||
Substituindo a nova expressão acima no método de FTCS discutido anteriormente, encontramos o método de Leapfrog: | |||
<math>\textbf{U}^{n+1}_i = \textbf{U}^{n-1}_i - \frac{\Delta t}{\Delta x} [\textbf{F}^n_{i+1} - \textbf{F}^n_{i-1}] + \mathcal{O}(\Delta x^2).</math> | |||
Como o método de Leapfrog será o mais aplicado na resolução do problema da onda, é interessante um aprofundamento maior do método. Podemos adaptar o método de Leapfrog para o sistema de equações definido para a equação da onda ao fazermos a discretização ao redor de um ponto qualquer <math>i</math> no instante de tempo <math>n</math>: | |||
<math> | |||
k_{i+\frac{1}{2}}^n \equiv v \left.\frac{\partial U}{\partial x}\right|_{i+\frac{1}{2}}^{n} = v \frac{U_{i+1}^n-U_i^n}{\Delta x} + \mathcal{O}(\Delta x) \qquad (1) | |||
</math> | |||
<math> | |||
s_{i}^{n+\frac{1}{2}} \equiv \left.\frac{\partial U}{\partial t}\right|_{i}^{n+\frac{1}{2}} = \frac{U_{i}^{n+1}-U_i^n}{\Delta t} + \mathcal{O}(\Delta t) \qquad (2) | |||
</math> | |||
Com essas discretizações, podemos utilizar as equações (1) e (2) para resolvermos para <math>k^{n+1}_{i+\frac{1}{2}}</math> apenas em termos de <math>s</math>, <math>k</math> e <math>r</math>. Fazendo as substituições dessas duas equações uma na outra (ver passo a passo: [[Dedução Leapfrog]]), obtemos: | |||
<math>\frac{\Delta x}{v}k^{n+1}_{i+\frac{1}{2}} = s^{n+\frac{1}{2}}_{i+1}\Delta t + \frac{\Delta x}{v}k^{n}_{i+\frac{1}{2}} + U^n_i - (s^{n+\frac{1}{2}}_i \Delta t + U^n_i)</math> | |||
Dessa equação, chegamos a | |||
<math> | |||
k_{i+\frac{1}{2}}^{n+1} = k_{i+\frac{1}{2}}^n+r(s_{i+1}^{n+\frac{1}{2}}-s_{i}^{n+\frac{1}{2}}) \qquad (3) | |||
</math> | |||
Utilizando o mesmo raciocínio, podemos também resolver para <math>s^{n+\frac{1}{2}}_i</math> e obter | |||
<math> | |||
s_i^{n+\frac{1}{2}} = s_{i}^{n-\frac{1}{2}}+r(k_{i+\frac{1}{2}}^{n}-k_{i-\frac{1}{2}}^{n}) \qquad (4) | |||
</math> | |||
Com essas duas equações, podemos fazer uma integração utilizando o método de Euler para obter <math>U_i^{n+1}</math>, ou seja, o deslocamento de um determinado ponto <math>i</math> da corda no próximo instante de tempo: | |||
<math>U_i^{n+1} = U_i^n + \frac{\Delta t}{2}s_i^{n+\frac{1}{2}}+\mathcal{O}(\Delta x^2).</math> | |||
Contudo, podemos fazer uma simples substituição das equações <math>(1)</math> e <math>(2)</math> nas equações <math>(3)</math> e <math>(4)</math> e, assim, obtemos que a representação de Leapfrog da equação da onda é dada pela discretização de segunda ordem da própria equação da onda, com <math>\mathcal{O}(\Delta t^2, \Delta x^2)</math> (ver passo a passo da comparação [[Discretização x Leapfrog]]. Isso nos dá uma solução de "um passo", onde só precisamos efetuar o cálculo da equação discretizada pelo método da derivação finita, ou seja, para o caso da corda ideal, a equação | |||
<math>U_i^{n+1} = 2(1-r^2)U_i^n + r^2[U_{i+1}^n+U_{i-1}^n]-U_i^{n-1}.</math> | |||
=== O Método de Lax-Wendroff === | === O Método de Lax-Wendroff === | ||
| Linha 114: | Linha 212: | ||
O método de Lax-Wendroff é a extensão do método de Lax-Friedrichs de segunda ordem. Calculamos o vetor <math>U</math> a partir de um passo médio de Lax-Friedrichs: | O método de Lax-Wendroff é a extensão do método de Lax-Friedrichs de segunda ordem. Calculamos o vetor <math>U</math> a partir de um passo médio de Lax-Friedrichs: | ||
<math>\textbf{U}^{n+\frac{1}{2}}_{ | <math>\textbf{U}^{n+\frac{1}{2}}_{i + \frac{1}{2}} = \frac{1}{2} [\textbf{U}^n_{i+1} + \textbf{U}^n_i] - \frac{\Delta t}{2 \Delta x} [\textbf{F}^n_{i+1} - \textbf{F}^n_i] + \mathcal{O}(\Delta x^2)</math>, | ||
<math>\textbf{U}^{n+\frac{1}{2}}_{ | <math>\textbf{U}^{n+\frac{1}{2}}_{i - \frac{1}{2}} = \frac{1}{2} [\textbf{U}^n_{i} + \textbf{U}^n_{i-1}] - \frac{\Delta t}{2 \Delta x} [\textbf{F}^n_{i} - \textbf{F}^n_{i-1}] + \mathcal{O}(\Delta x^2)</math>, | ||
E encontramos os fluxos <math>\textbf{F}^{n+\frac{1}{2}}_{ | E encontramos os fluxos <math>\textbf{F}^{n+\frac{1}{2}}_{i \pm \frac{1}{2}}</math> a partir dos valores de <math>\textbf{U}^{n+\frac{1}{2}}_{i \pm \frac{1}{2}}.</math> | ||
Logo, com um meio passo de Leapfrog, temos a expressão final do método: | Logo, com um meio passo de Leapfrog, temos a expressão final do método: | ||
<math>\textbf{U}^{n+1} | <math>\textbf{U}^{n+1}_i = \textbf{U}^n_i - \frac{\Delta t}{\Delta x} \left[\textbf{F}^{n + \frac{1}{2}}_{i + \frac{1}{2}} - \textbf{F}^{n + \frac{1}{2}}_{i - \frac{1}{2}}\right] + \mathcal{O}(\Delta x^2)</math> | ||
== Análise e Discussão dos Resultados == | |||
Escolhemos para simular quatro diferentes cordas: as cordas C2, C4 e C7, que são cordas dó de um piano <ref>Antoine Chaign, Anders Askenfelt, "Numerical simulations of piano strings. I. A physical model for a struck string using finite difference methods". Signal Department, Paris, France. Department of Speech Communication and Music Acoustics; Royal Institute of Technology, Stockholm, Sweden.</ref> e uma corda qualquer baseada nos dados encontrados no livro "''Computational Physics''" <ref name=giordano/>. Os dados das cordas C2, C4 e C7 estão na tabela abaixo, onde iremos definir para cada corda o comprimento, a massa, a tensão aplicada elas, o número de divisões existentes, amostragem de sinal (que é um parâmetro obtido experimentalmente)e o parâmetro de fricção. | |||
{| class="wikitable" | |||
|- | |||
! | |||
! '''C2''' | |||
! '''C4''' | |||
! '''C7''' | |||
|- | |||
| '''Comprimento''' (<math>m</math>) | |||
| <math>1.90</math> | |||
| <math>0.62</math> | |||
| <math>0.09</math> | |||
|- | |||
| '''Massa'''(<math>g</math>) | |||
| <math>35</math> | |||
| <math>3.93 </math> | |||
| <math>0.467</math> | |||
|- | |||
| '''Tensão''' (<math>N</math>) | |||
| <math>750</math> | |||
| <math>670</math> | |||
| <math>750</math> | |||
|- | |||
| '''Divisões''' | |||
| <math>100</math> | |||
| <math>50</math> | |||
| <math>16</math> | |||
|- | |||
| '''Amostragem de sinal''' | |||
| <math>16\times10^{3}</math> | |||
| <math>32\times10^{3}</math> | |||
| <math>96\times10^{3}</math> | |||
|- | |||
|'''Parâmetro de fricção''' | |||
| <math>7.5\times10^{-6}</math> | |||
| <math>3.82\times10^{-5}</math> | |||
| <math>8.67\times10^{-4}</math> | |||
|} | |||
Desses dados, temos que a densidade linear de massa das cordas é dada por | |||
<math>\rho = \frac{M}{L},</math> | |||
onde <math>M</math> é a massa e <math>L</math> o comprimento da corda, | |||
<math>v = \sqrt{\frac{T}{\rho}},</math> | |||
onde <math>T</math> é a tensão na corda, | |||
<math>\Delta x = \frac{L}{K},</math> | |||
<math>\Delta t = \frac{1}{f_e},</math> | |||
e | |||
<math>r = v\frac{\Delta t}{\Delta x}.</math> | |||
Os dados obtidos a partir de todas essas equações são calculados pelo programa com base dos dados da tabela. | |||
Para a simulação baseada nos dados retirados do livro ''"Computational Physics"''<ref name=giordano/>, utilizamos uma corda com 2 metros de comprimento, com velocidade de propagação transversal da onda sendo 300<math>m/s</math>, <math>\Delta x</math> de 0.01<math>m</math>, <math>\Delta t = \frac{\Delta x }{4v}</math> e parâmetro de fricção de <math>7.5\times10^{-6}</math>. | |||
Supondo uma corda inicialmente em repouso, temos que em <math>t = 0</math> a corda irá receber em seu centro o equivalente à batida do martelo de um piano. Supomos que esse estímulo da batida do martelo possuía o formato aproximado de uma Gaussiana com amplitude de <math>\frac{1}{4}</math> do comprimento de cada corda. | |||
Então, com o estado inicial da simulação sendo um pulso com o formato de um pacote gaussiano, utilizando condições de contorno fixas, ou seja, mantendo as extremidades da corda paradas e utilizando os dados da tabela para simularmos cada uma das cordas, começamos a simular a propagação de ondas. | |||
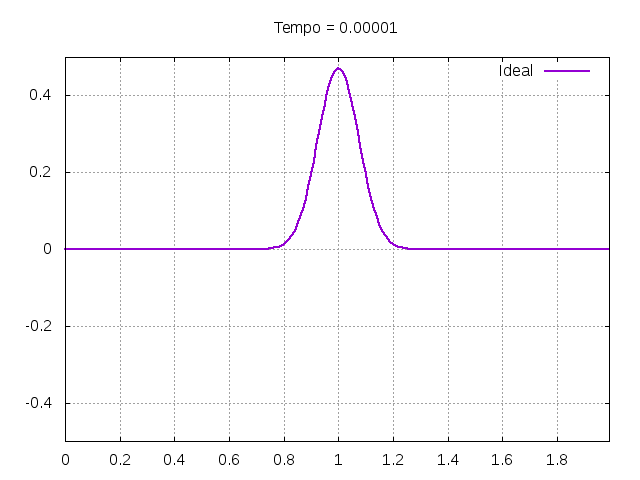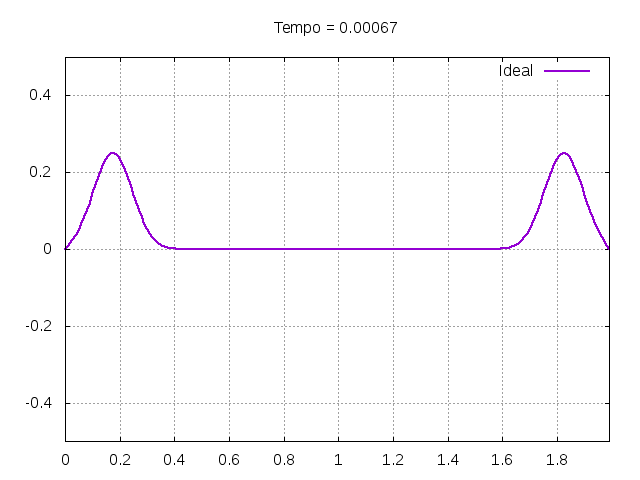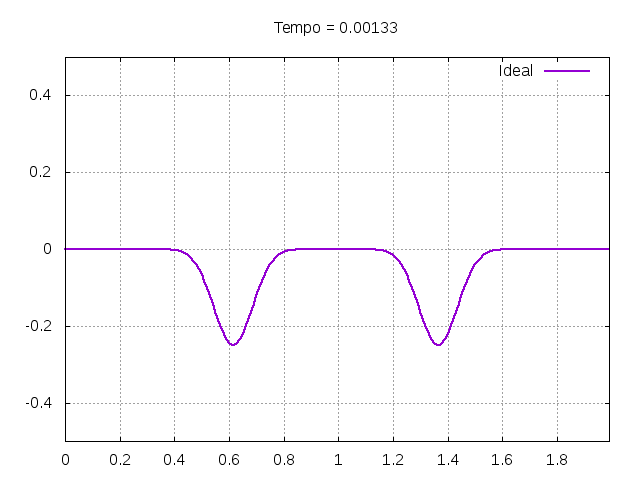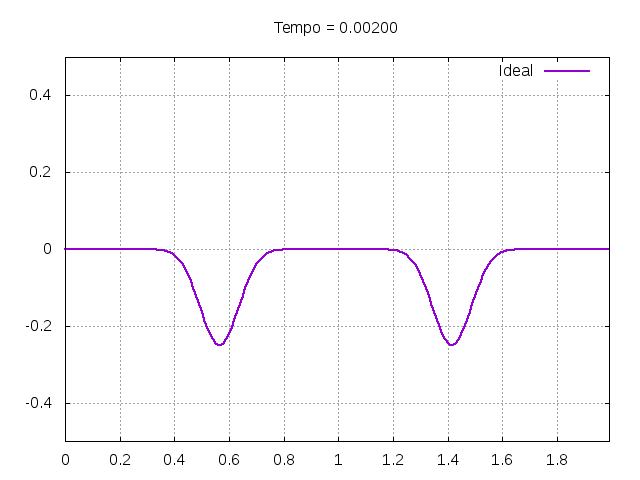
Utilizando o método de Leapfrog, foi realizada uma primeira simulação para uma onda ideal em uma corda: | |||
[[File:ideal.gif|frame|none|alt=Alt text|Simulação de uma onda em uma corda ideal com condições de contorno u(0,t) = 0 e u(L,t) = 0. A corda simulada possuía comprimento de 2 metros e a amplitude inicial do pulso gaussiano tinha amplitude de 0.5 metros. Foi utilizado uma velocidade de propagação de 300 m/s, <math>\Delta x = 0.01</math> e <math>\Delta t = \frac{\Delta x }{4v}</math>.]] | |||
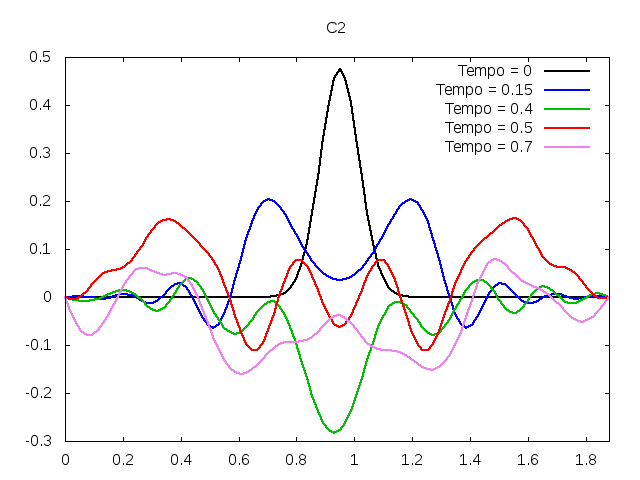
'''Corda C2:''' | |||
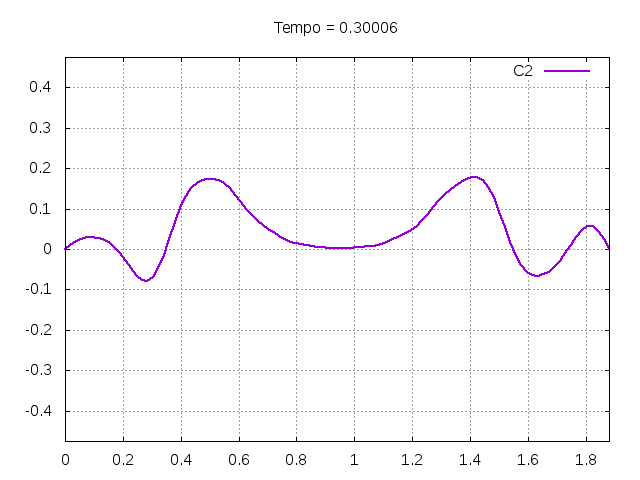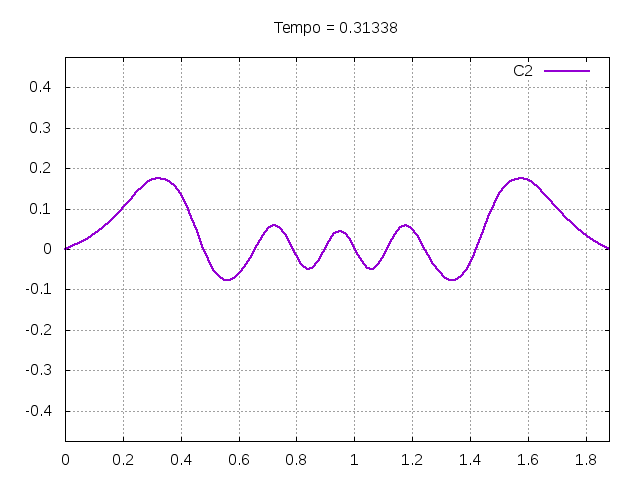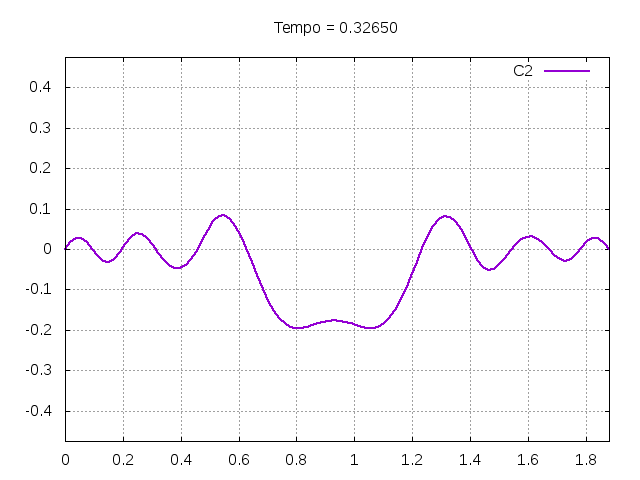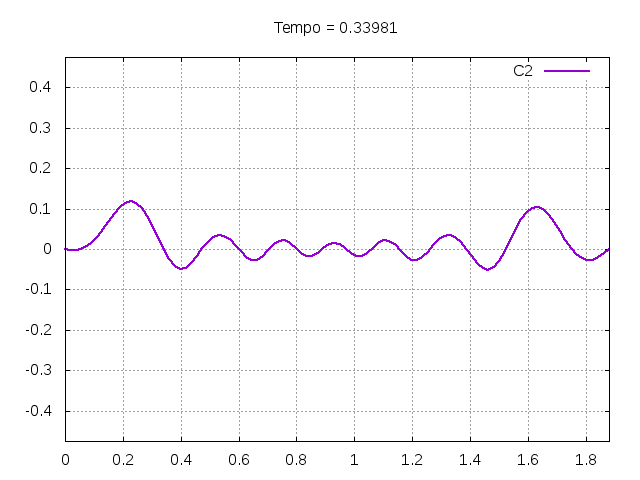
[[Arquivo:C2.gif|frame|none|alt=Alt text|Simulação de uma corda C2 de um piano com os parâmetros da tabela acima.]][[Arquivo:C2foto.png|frame|none|alt=Alt text|Estado da corda C2 em diferentes instantes de tempo.]] | |||
'''Corda C4:''' | |||
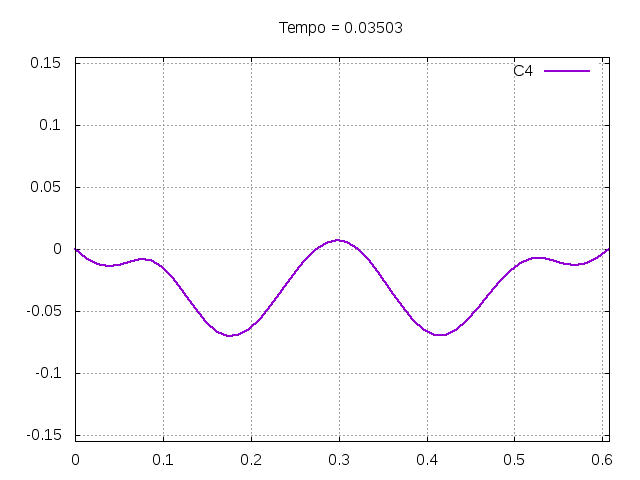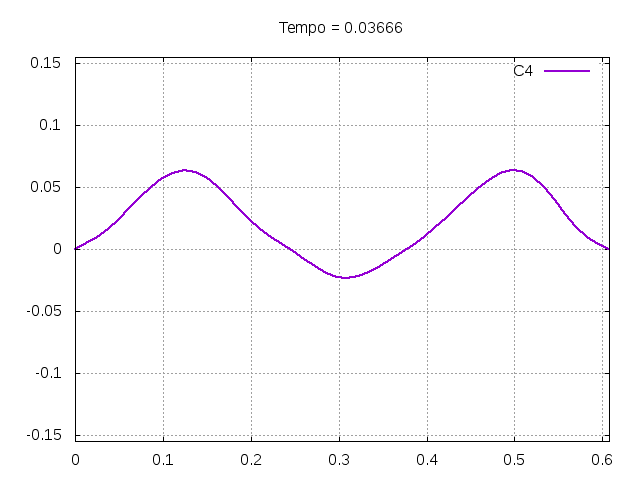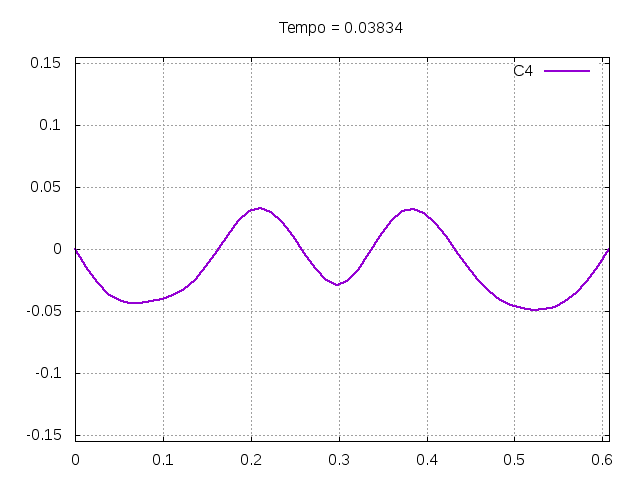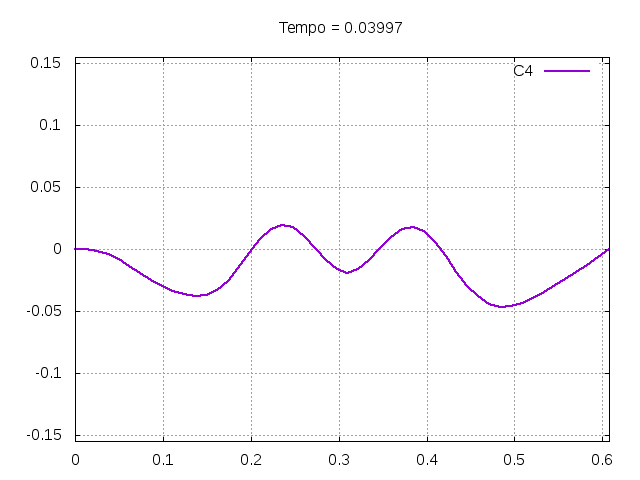
[[Arquivo:C4.gif|frame|none|alt=Alt text|Simulação de uma corda C4 de um piano com os parâmetros da tabela acima.]] | |||
[[Arquivo:C4foto.png|frame|none|alt=Alt text|Estado da corda C4 em diferentes instantes de tempo.]] | |||
'''Corda C7:''' | |||
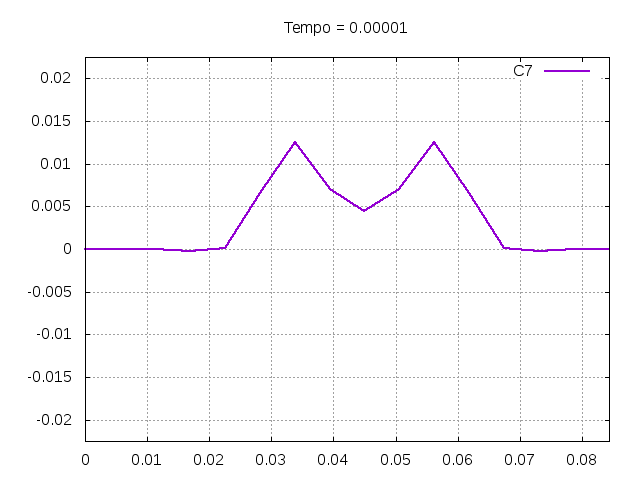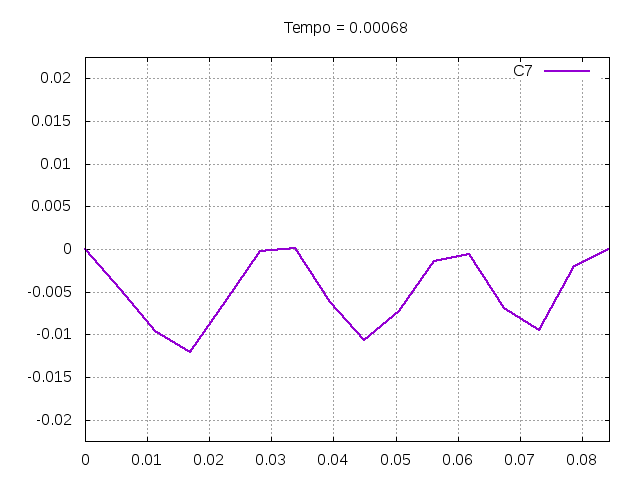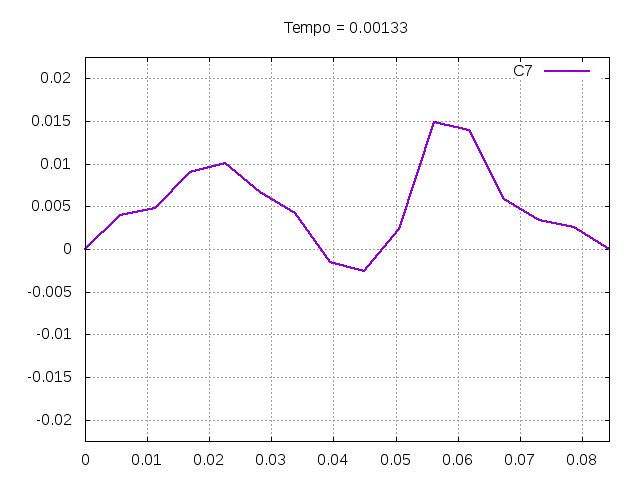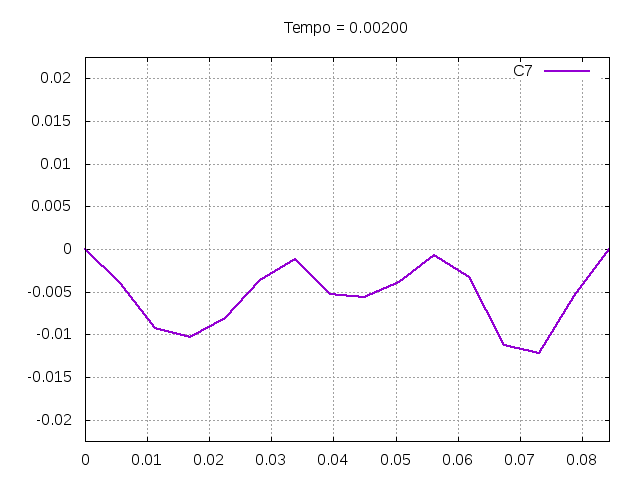
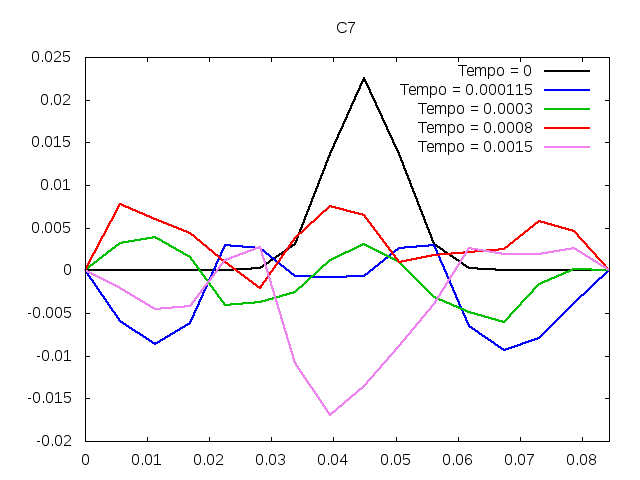
[[Arquivo:C7.gif|frame|none|alt=Alt text|Simulação de uma corda C7 de um piano com os parâmetros da tabela acima.]] | |||
[[Arquivo:C7foto.png|frame|none|alt=Alt text|Estado da corda C7 em diferentes instantes de tempo.]] | |||
'''Corda com as definições do livro "''Computational Physics''"<ref name=giordano/>:''' | |||
[[Arquivo:Giordano.gif|frame|none|alt=Alt text|Simulação da corda exemplificada no livro ''Computational Physics'' <ref name=giordano/>. Os parâmetros utilizados estão descritos no texto.]] | |||
[[Arquivo:Giordanofoto.png|frame|none|alt=Alt text|Estado da corda usada como exemplo pelo autor Giordano <ref name=giordano/> em diferentes instantes de tempo.]] | |||
É possível observar que o tempo necessário para que, devido a fricção, os movimentos na corda diferenciem-se cada vez mais da solução para a corda ideal é menor para um tamanho de corda menor, ou seja, a fricção acaba sendo mais relevante mais rapidamente em cordas mais curtas. Isso significa que deixamos de ter apenas dois pulsos propagando-se em sentidos opostos para termos ou mais pulsos de amplitudes menores, ou a soma de pulsos de diferentes amplitudes. | |||
=== Scripts para a simulação dos resultados apresentados: === | |||
[[Programa baseado no método de Leapfrog para a simulação de uma corda ideal]] | |||
[[Programa baseado no método de Leapfrog para a simulação de uma corda real]] | |||
== Análise de Erro e Estabilidade dos Métodos == | |||
=== Estabilidade do método Leapfrog === | |||
Pela estabilidade de Von Neumann, podemos escrever que | |||
<math> | |||
r \leq 1. | |||
</math> | |||
Para <math>r = 1</math>, a equação da discretização da onda pode ser reescrita como | |||
<math>U_i^{n+1} = U_{i+1}^n+U_{i-1}^n-U_i^{n-1}.</math> | |||
Essa escolha com | |||
<math>\frac{\Delta x}{\Delta t} = v</math> | |||
nos dá a solução exata sem dispersão numérica, como pode ser verificado pela condição CFL. Contudo, <math>r=1</math> é válido somente no caso de uma corda ideal. | |||
É conveniente escrever a condição acima em termos da amostragem de sinal <math>f_e = \frac{1}{\Delta t}</math> e a frequência fundamental da corda <math>f_1 = \frac{v}{2L}</math>, o que nos leva a | |||
<math> | |||
Kf_1 \leq \frac{f_e}{2} | |||
</math> | |||
O[https://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem Teorema de Nyquist-Shannon] diz que a frequência superior no espectro deve ser menor do que <math>\frac{f_e}{2}</math> para evitar serrilhamento e para garantir uma reconstrução única e contínua. Logo, no caso ideal quando as autofrequências da corda são igualmente espaçadas (<math>\Delta f = f_1</math>), a condição de Nyquist indica que o número máximo de frequências no espectro é <math>K</math>. Isso significa que essa condição pode ser usada para selecionar o número apropriado de pontos espaciais <math>K</math> para a corda. Entretanto, como <math>K</math> é um inteiro, apenas valores discretos da frequência natural podem ser obtidos sem erros de trucamento, ou seja, usando <math>r = 1</math>. Como séries discretas não costumam ser utilizadas, precisamos aceitar pequenos erros de truncamento para ajustar <math>f_1</math>, ou seja, utilizando <math>r < 1</math>. No caso de uma onda com fricção, temos que <math>r=\frac{1}{4}</math> é um valor de boa estabilidade. | |||
== Referências Bibliográficas== | |||
<references/> | |||
Edição atual tal como às 16h30min de 26 de janeiro de 2018
Grupo: Lucas Dória, Caetano Pires e Ânderson Rosa.
O objetivo deste trabalho é analisar três métodos diferentes de integração numérica para resolução de equações diferenciais parciais (EDP's). A equação aqui abordada é a equação da onda, a qual consiste em uma EDP hiperbólica de segunda ordem. Uma pequena noção dos métodos numéricos é dada, após a explicação do problema físico abordado. Os dados encontrados são comentados e comparados com os resultados esperados. Simulações também foram feitas para melhor visualização dos fenômenos. Por último, foi feita uma análise de erros e estabilidade para cada um dos métodos, assim como algumas conclusões foram inferidas.
Introdução
Equações diferenciais parciais hiperbólicas geralmente podem ser formuladas a partir de teoremas de conservação. Um exemplo é a equação do tipo:
onde é o vetor de densidades da quantidade conservada, i.e., é o fluxo de densidade e é um termo genérico representando fontes e/ou sumidouros.
Uma classe especial de equações hiperbólicas são as chamadas equações de adveção, na qual a derivada temporal da quantidade conservada é proporcional à sua derivada espacial. Nesses casos, é diagonal e dada por:
onde é a matriz identidade.
Considerando apenas uma dimensão e com , temos a equação de adveção:
onde é a velocidade de propagação do pulso gerado. A equação admite uma solução analítica da forma representando um pulso se movendo na direção positiva de
A equação da onda em uma dimensão é uma EDP hiperbólica de segunda ordem dada por
onde é o deslocamento transversal à direção de propagação de uma posição no instante e admite duas soluções, representadas por pulsos, na forma e
Assumindo que não depende da posição na equação da onda, nos restringimos a problemas lineares. Além disso, se escrevermos
então a equação da onda pode ser escrita como um sistema de três equações diferenciais de primeira ordem:
Em notação vetorial, o sistema acima pode ser reescrito na forma conservativa como:
onde
Condição CFL
Uma condição necessária mas nem sempre suficiente para a convergência de equações diferenciais parciais resolvidas a partir de métodos de diferença, conhecida como condição CFL [1], é formulada a partir do termo de “domínio de dependência”.
Considerando, por exemplo, a equação da advecção [1] em uma aproximação a partir de métodos de diferença em sua forma explícita
diz-se que o valor de depende dos valores anteriores de e , e esses dois pontos dependem, novamente, de outros dois pontos em tempos anteriores. Todos esses pontos dependentes formam o domínio de dependência do valor , representado abaixo (botar figura do domínio de dependência).
A condição CFL enuncia que a condição mínima para que haja estabilidade em métodos de diferenças o domínio de dependência da equação diferencia parcial, dado por sua equação característica, deve estar situado dentro do domínio de dependência do esquema numérico.
A partir dessa condição, define-se o número CFL como
onde é um passo na malha temporal e é um passo na malha espacial. Para casos unidimensionais, como o que será tratado aqui, a condição CFL é satisfeita se r
Um uso da condição CFL é determinar o tamanho do passo temporal, sabendo-se e :
onde o fator .
O número CFL pode ser entendido como um fluxo numérico advectivo adimensionalisado pelas malhas espacial e temporal do problema. De um ponto de vista matemático, ele garante que o domínio numérico de dependência é sempre maior que o domínio físico. De um ponto de vista físico, é garantido que a velocidade de propagação de qualquer perturbação, como uma onda, seja menor ou ao menos igual que a velocidade de propagação numérica, fazendo com que a distância propagada pela perturbação não seja maior do que a divisão da malha espacial:
O Problema Físico
O Modelo de Corda Ideal
Para uma primeira abordagem da equação da onda, consideramos uma corda com suas extremidades fixas. Podemos dividir o comprimento dessa corda em intervalos de comprimentos iguais, dessa forma . Cada intervalo é discretizado, representado por , . Também podemos dividir o tempo em intervalos iguais e denotá-los como , . Abaixo temos uma esquematização das informações que precisamos para cada ponto da corda:
Tendo feita a discretização das variáveis, podemos aproximar a equação da onda por diferenciação finita, utilizando derivadas centradas da seguinte forma:
onde representa o valor discretizado de .
Assim, chegamos em uma equação discretizada:
.
Sabendo que essa discretização da equação da onda pode ser verificada como sendo o método Leapfrog (ver seção do método de Leapfrog método de Leapfrog), podemos resolver a equação para para sabermos o deslocamento vertical de uma partição da corda no momento de tempo seguinte, assim obtendo
,
onde
Um Quadro Mais Realístico - O Modelo de Corda Rígida
Para nos aproximarmos de um modelo mais real, podemos adicionar um termo à equação original da onda que corresponde ao efeito de fricção em uma corda. A equação da onda mais geral com efeito de fricção pode ser escrita como: [2]
onde é a velocidade transversal de propagação do pulso na corda, dada pela relação (sendo a tensão na corda e a densidade linear da mesma), é um parâmetro adimensional de fricção que representa a rigidez da corda e o comprimento da corda.
O parâmetro é dado por
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \kappa² \frac{E S}{T L^2}} ,
onde é o raio de giro da corda, é o Módulo de Young e a área da secção da corda.
Discretizamos a equação da seguinte maneira:
e resolvemos para , obtendo:
O fato de essa discretização depender do deslocamento da corda em posições e implica em precisarmos simular "pontos fantasmas" quando integramos os extremos das cordas. Para fazermos isso, podemos ou utilizar a aproximação ou podemos considerar esses "pontos fantasmas" como pontos presos e, portanto, sempre iguais a zero.
Os Métodos Utilizados
Foi realizada uma abordagem ao problema da corda real a partir de três métodos diferentes de integração numérica.
O método mais básico é chamado de FTCS (Forward-Time-Centered-Space) e consiste em duas expansões de Taylor ao redor do ponto :
Subtraindo as duas expressões, encontramos a expressão
,
A qual podemos substituir na equação da onda, juntamente com a discretização da derivada parcial temporal. Temos então que, para um sistema linear de equações hiperbólicas:
Visto que essa última notação é mais genérica, ela será utilizada para a explicação dos métodos posteriores.
O Método de Lax-Friedrichs
O método de Lax-Friedrichs consiste em substituir o termo com sua respectiva média espacial, i.e., . Logo, temos a seguinte equação de recorrência:
O Método de Leapfrog
Tanto o método FTCS quanto o método de Lax-Friedrichs são métodos de primeira ordem para a derivada temporal. Nessas circunstâncias, deve ser significantemente menor do que , muito abaixo do limite imposto pela condição de Courant.
Uma nova expressão para a derivada temporal, com precisão de segunda ordem é dada por
Substituindo a nova expressão acima no método de FTCS discutido anteriormente, encontramos o método de Leapfrog:
Como o método de Leapfrog será o mais aplicado na resolução do problema da onda, é interessante um aprofundamento maior do método. Podemos adaptar o método de Leapfrog para o sistema de equações definido para a equação da onda ao fazermos a discretização ao redor de um ponto qualquer no instante de tempo :
Com essas discretizações, podemos utilizar as equações (1) e (2) para resolvermos para apenas em termos de , e . Fazendo as substituições dessas duas equações uma na outra (ver passo a passo: Dedução Leapfrog), obtemos:
Dessa equação, chegamos a
Utilizando o mesmo raciocínio, podemos também resolver para e obter
Com essas duas equações, podemos fazer uma integração utilizando o método de Euler para obter , ou seja, o deslocamento de um determinado ponto da corda no próximo instante de tempo:
Contudo, podemos fazer uma simples substituição das equações e nas equações e e, assim, obtemos que a representação de Leapfrog da equação da onda é dada pela discretização de segunda ordem da própria equação da onda, com (ver passo a passo da comparação Discretização x Leapfrog. Isso nos dá uma solução de "um passo", onde só precisamos efetuar o cálculo da equação discretizada pelo método da derivação finita, ou seja, para o caso da corda ideal, a equação
O Método de Lax-Wendroff
O método de Lax-Wendroff é a extensão do método de Lax-Friedrichs de segunda ordem. Calculamos o vetor a partir de um passo médio de Lax-Friedrichs:
,
,
E encontramos os fluxos a partir dos valores de
Logo, com um meio passo de Leapfrog, temos a expressão final do método:
Análise e Discussão dos Resultados
Escolhemos para simular quatro diferentes cordas: as cordas C2, C4 e C7, que são cordas dó de um piano [3] e uma corda qualquer baseada nos dados encontrados no livro "Computational Physics" [2]. Os dados das cordas C2, C4 e C7 estão na tabela abaixo, onde iremos definir para cada corda o comprimento, a massa, a tensão aplicada elas, o número de divisões existentes, amostragem de sinal (que é um parâmetro obtido experimentalmente)e o parâmetro de fricção.
| C2 | C4 | C7 | |
|---|---|---|---|
| Comprimento () | |||
| Massa() | |||
| Tensão () | |||
| Divisões | |||
| Amostragem de sinal | |||
| Parâmetro de fricção |
Desses dados, temos que a densidade linear de massa das cordas é dada por
onde é a massa e o comprimento da corda,
onde é a tensão na corda,
e
Os dados obtidos a partir de todas essas equações são calculados pelo programa com base dos dados da tabela.
Para a simulação baseada nos dados retirados do livro "Computational Physics"[2], utilizamos uma corda com 2 metros de comprimento, com velocidade de propagação transversal da onda sendo 300, de 0.01, e parâmetro de fricção de .
Supondo uma corda inicialmente em repouso, temos que em a corda irá receber em seu centro o equivalente à batida do martelo de um piano. Supomos que esse estímulo da batida do martelo possuía o formato aproximado de uma Gaussiana com amplitude de do comprimento de cada corda.
Então, com o estado inicial da simulação sendo um pulso com o formato de um pacote gaussiano, utilizando condições de contorno fixas, ou seja, mantendo as extremidades da corda paradas e utilizando os dados da tabela para simularmos cada uma das cordas, começamos a simular a propagação de ondas.
Utilizando o método de Leapfrog, foi realizada uma primeira simulação para uma onda ideal em uma corda:
Corda C2:
Corda C4:
Corda C7:
Corda com as definições do livro "Computational Physics"[2]:
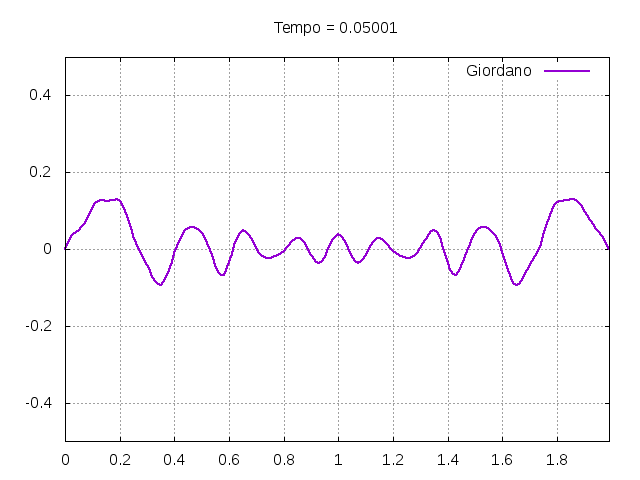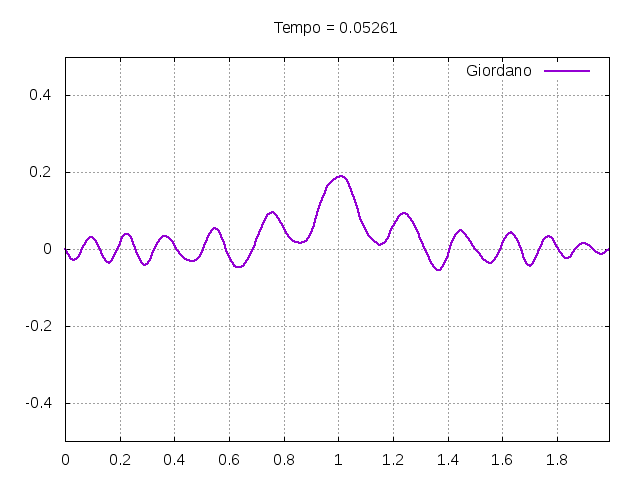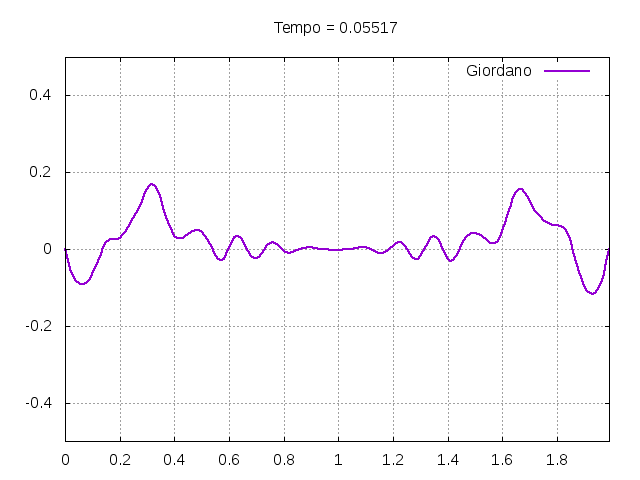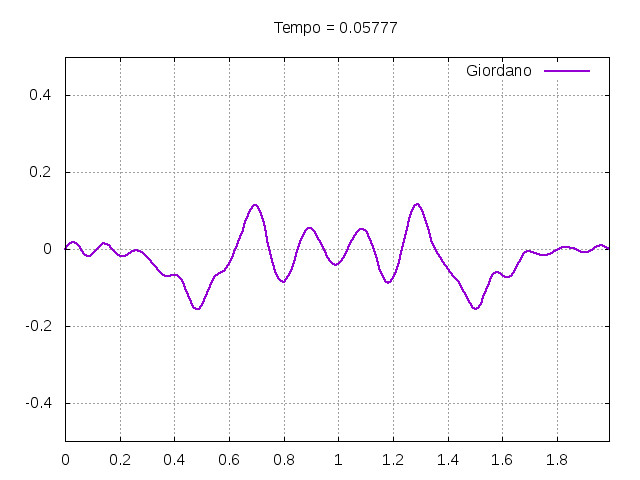

É possível observar que o tempo necessário para que, devido a fricção, os movimentos na corda diferenciem-se cada vez mais da solução para a corda ideal é menor para um tamanho de corda menor, ou seja, a fricção acaba sendo mais relevante mais rapidamente em cordas mais curtas. Isso significa que deixamos de ter apenas dois pulsos propagando-se em sentidos opostos para termos ou mais pulsos de amplitudes menores, ou a soma de pulsos de diferentes amplitudes.
Scripts para a simulação dos resultados apresentados:
Programa baseado no método de Leapfrog para a simulação de uma corda ideal
Programa baseado no método de Leapfrog para a simulação de uma corda real
Análise de Erro e Estabilidade dos Métodos
Estabilidade do método Leapfrog
Pela estabilidade de Von Neumann, podemos escrever que
Para , a equação da discretização da onda pode ser reescrita como
Essa escolha com
nos dá a solução exata sem dispersão numérica, como pode ser verificado pela condição CFL. Contudo, é válido somente no caso de uma corda ideal. É conveniente escrever a condição acima em termos da amostragem de sinal e a frequência fundamental da corda , o que nos leva a
OTeorema de Nyquist-Shannon diz que a frequência superior no espectro deve ser menor do que para evitar serrilhamento e para garantir uma reconstrução única e contínua. Logo, no caso ideal quando as autofrequências da corda são igualmente espaçadas (), a condição de Nyquist indica que o número máximo de frequências no espectro é . Isso significa que essa condição pode ser usada para selecionar o número apropriado de pontos espaciais para a corda. Entretanto, como é um inteiro, apenas valores discretos da frequência natural podem ser obtidos sem erros de trucamento, ou seja, usando . Como séries discretas não costumam ser utilizadas, precisamos aceitar pequenos erros de truncamento para ajustar , ou seja, utilizando . No caso de uma onda com fricção, temos que é um valor de boa estabilidade.
Referências Bibliográficas
- ↑ Luciano Rezzolla, "Numerical Methods for the Solution of Partial Differential Equations". Albert Einstein Institute, Max-Planck-Institute for Gravitational Physics, Potsdam, Germany.
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 N. J. Giordano, "Computational Physics". Department of Physics, Purdue University. Upper Saddle River, New Jersey. Prentice-Hall, 1997.
- ↑ Antoine Chaign, Anders Askenfelt, "Numerical simulations of piano strings. I. A physical model for a struck string using finite difference methods". Signal Department, Paris, France. Department of Speech Communication and Music Acoustics; Royal Institute of Technology, Stockholm, Sweden.














































![{\displaystyle U_{i}^{n+1}=2(1-r^{2})U_{i}^{n}+r^{2}[U_{i+1}^{n}+U_{i-1}^{n}]-U_{i}^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ffc557229be16dc91d5c8d5f1b185c80634fdc6)


![{\displaystyle v={\sqrt[{}]{\frac {T}{\rho }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d9f8b0e2989b05536891f8e25fda20ccbb73526)







![{\displaystyle U_{i}^{n+1}=[2-2r^{2}-6\epsilon r^{2}K^{2}]U_{i}^{n}-U_{i}^{n-1}+r^{2}[1+4\epsilon K^{2}][U_{i+1}^{n}+U_{i-1}^{n}]-\epsilon r^{2}K^{2}[U_{i+2}^{n}+U_{i-2}^{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/211aa432ea15c7e195cc58bbdd0ad03b2536e306)







![{\displaystyle {\textbf {U}}_{i}^{n+1}={\textbf {U}}_{i}^{n}-{\frac {\Delta t}{2\Delta x}}[{\textbf {F}}_{i+1}^{n}-{\textbf {F}}_{i-1}^{n}]+{\mathcal {O}}(\Delta t^{2},\Delta x^{2}\Delta t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51ac12307e68a12c8ab66c9312f54684d89846d5)


![{\displaystyle {\textbf {U}}_{i}^{n+1}={\frac {1}{2}}({\textbf {U}}_{i+1}^{n}+{\textbf {U}}_{i-1}^{n})-{\frac {\Delta t}{2\Delta x}}[{\textbf {F}}_{i+1}^{n}-{\textbf {F}}_{i-1}^{n}]+{\mathcal {O}}(\Delta x^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cadf13cfb2bac2263a9998aeaaae5652bc93890)


![{\displaystyle {\textbf {U}}_{i}^{n+1}={\textbf {U}}_{i}^{n-1}-{\frac {\Delta t}{\Delta x}}[{\textbf {F}}_{i+1}^{n}-{\textbf {F}}_{i-1}^{n}]+{\mathcal {O}}(\Delta x^{2}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/143a9dffff0e2f8819d6e4986ee0b01d8c244c90)


















![{\displaystyle U_{i}^{n+1}=2(1-r^{2})U_{i}^{n}+r^{2}[U_{i+1}^{n}+U_{i-1}^{n}]-U_{i}^{n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4559fc34448f3e3c8207bab9e3da829caa195d2a)

![{\displaystyle {\textbf {U}}_{i+{\frac {1}{2}}}^{n+{\frac {1}{2}}}={\frac {1}{2}}[{\textbf {U}}_{i+1}^{n}+{\textbf {U}}_{i}^{n}]-{\frac {\Delta t}{2\Delta x}}[{\textbf {F}}_{i+1}^{n}-{\textbf {F}}_{i}^{n}]+{\mathcal {O}}(\Delta x^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/287437c2bdd37c022e3ac7027d372cdb630e49ca)
![{\displaystyle {\textbf {U}}_{i-{\frac {1}{2}}}^{n+{\frac {1}{2}}}={\frac {1}{2}}[{\textbf {U}}_{i}^{n}+{\textbf {U}}_{i-1}^{n}]-{\frac {\Delta t}{2\Delta x}}[{\textbf {F}}_{i}^{n}-{\textbf {F}}_{i-1}^{n}]+{\mathcal {O}}(\Delta x^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a6138d7da4c4f0d90cbbf6a9adb1de606489ee8)


![{\displaystyle {\textbf {U}}_{i}^{n+1}={\textbf {U}}_{i}^{n}-{\frac {\Delta t}{\Delta x}}\left[{\textbf {F}}_{i+{\frac {1}{2}}}^{n+{\frac {1}{2}}}-{\textbf {F}}_{i-{\frac {1}{2}}}^{n+{\frac {1}{2}}}\right]+{\mathcal {O}}(\Delta x^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42b9230c78f4be4096d5c5f0301ec35296fcdfe4)