Modelo de Lotka-Volterra amortecido: mudanças entre as edições
(Criou página com '{{Ecologia| [Modelo de Lotka-Volterra amortecido |Modelo de Levins}} {{Ecologia| [Modelo de Lotka-Volterra amortecido |Modelo de Levins}}') |
Sem resumo de edição |
||
| (6 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| | __NOTOC__ | ||
{{Ecologia| | {{Ecologia| [[Modelo de Lotka-Volterra]] |[[Modelo de Levins aprimorado para 2 espécies | Modelo de Levins aprimorado para 2 espécies I]]}} | ||
Uma versão do modelo de Lotka-Volterra aprimorada inclui um termo de saturação na população de presas, isto é, um termo logístico (que inibe o aumento exponencial) visando representar a finitude dos recursos disponíveis para uma espécie. Este modelo é chamado de modelo de Lotka-Volterra amortecido. | |||
* <math display="inline">\frac{dx}{dt}=x\left(a-\alpha y\right)-kx^{2}</math> | |||
* <math display="inline">\frac{dy}{dt}=y\left(-c+\gamma x\right)</math> | |||
Onde <math display="inline">k</math> é uma constante positiva. Agora temos três pontos de equilíbrio, novamente temos <math display="inline">\left(0,0\right)</math>. Mas temos outro ponto quando apenas <math display="inline">y=0</math>: | |||
<math display="block">a-\alpha y-kx=a-kx=0\rightarrow x=\frac{a}{k}</math> | |||
Então <math display="inline">\left(\frac{a}{k},0\right)</math> ou seja um ponto de equilíbrio com apenas a sobrevivência da presa. E ainda temos também um ponto de coexistência entre ambas as espécies: | |||
<math display="block">a-\alpha y-kx=0</math><math display="block">-c+\gamma x=0</math> | |||
Isolando então <math display="inline">x</math> na segunda equação <math display="inline">x=\frac{c}{\gamma}</math> e substituindo na primeira: | |||
<math display="block">a-\alpha y-k\frac{c}{\gamma}=0</math>Então:<math display="block">y=\frac{a}{\alpha}-\frac{kc}{\alpha\gamma}=\frac{\gamma a-kc}{\alpha\gamma}</math> | |||
Então nosso outro ponto de equilíbrio é dado por<math display="inline">\left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)</math>. Infelizmente as equações não são separáveis como no caso anterior, portanto vamos analisar se a equação é semi-linear nas proximidades dos pontos de equilíbrio. Para <math display="inline">\left(0,0\right)</math>: | |||
<math display="block">\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha xy-kx^{2}}{xa}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha y-kx}{a}=0</math><math display="block">\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma xy}{cy}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}x=0</math> | |||
Para <math display="inline">\left(\frac{a}{k},0\right)</math> e fazendo a mudança de variáveis <math display="inline">u=x-\frac{a}{k}</math>, e <math display="inline">v=y</math>, temos: | |||
<math display="block">\frac{du}{dt}=\left(\left(u+\frac{a}{k}\right)a-k\left(u+\frac{a}{k}\right)^{2}\right)-\left(\alpha\left(u+\frac{a}{k}\right)v\right)</math><math display="block">\frac{du}{dt}=\left(ua+\frac{a^{2}}{k}-\left(u^{2}k+\frac{a^{2}}{k}+2ua\right)\right)-\left(\alpha uv+\frac{\alpha a}{k}v\right)</math><math display="block">\frac{du}{dt}=-\left(ua+\frac{\alpha a}{k}v\right)-\left(\alpha uv+u^{2}k\right)</math> | |||
E: | |||
<math display="block">\frac{dv}{dt}=\left(-vc\right)+\left(\gamma v\left(u+\frac{a}{k}\right)\right)=v\left(\gamma\frac{a}{k}-c\right)+\left(\gamma vu\right)</math> | |||
Então: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+u^{2}k}{ua+\frac{\alpha a}{k}v}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+u^{2}k}{u\left(a+\frac{\alpha a}{k}\frac{v}{u}\right)}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha v+uk}{\left(a+\frac{\alpha a}{k}\frac{v}{u}\right)}\right)</math> | |||
Podemos fazer uma substituição de variável novamente usando coordenadas polares<ref>[https://www.math.utah.edu/lectures/math2210/12PostNotes.pdf Limits and Continuity] (Rebecca Noonan-Heale ,Universidade de Utah)</ref> <math display="inline">r^{2}=u^{2}+v^{2}</math> e <math display="inline">u=r\cos\theta</math>, <math display="inline">v=r\sin\theta</math>, então: | |||
<math display="block">\lim_{r\rightarrow0}\left(\frac{\alpha r\sin\theta+kr\cos\theta}{\left(a+\frac{\alpha a}{k}\frac{r\sin\theta}{r\cos\theta}\right)}\right)=\lim_{r\rightarrow0}\left(\frac{\alpha kr\sin\theta+k^{2}r\cos\theta}{\left(ka+\alpha a\tan\theta\right)}\right)=0</math> | |||
E o limite: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma vu}{v\left(\gamma\frac{a}{k}-c\right)}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma u}{\left(\gamma\frac{a}{k}-c\right)}=0</math> | |||
E por fim, vamos estudar os pontos de estabilidade em torno de <math display="inline">\left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)</math>, tendo agora <math display="inline">u=x-\frac{c}{\gamma}</math> e <math display="inline">v=\frac{\gamma a-kc}{\alpha\gamma}-y</math>, então, manipulando novamente, primeiro trabalhando com <math>\dot{x}</math>: | |||
<math display="block">\frac{dx}{dt}=\left(xa-kx^{2}\right)-\left(\alpha xy\right)</math><math display="block">\frac{du}{dt}=\left(\left(\frac{c}{\gamma}+u\right)a-k\left(\frac{c}{\gamma}+u\right)^{2}\right)-\left(\alpha\left(\frac{c}{\gamma}+u\right)\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)\right)</math><math display="block">\frac{du}{dt}=\left(\frac{ca}{\gamma}+au-\frac{kc^{2}}{\gamma^{2}}-ku^{2}-\frac{2ck}{\gamma}u\right)-\left(\frac{c\alpha}{\gamma}v+\frac{\gamma ac-kc^{2}}{\gamma^{2}}+\alpha uv+\left[\frac{\gamma a-kc}{\gamma}\right]u\right)</math><math display="block">\frac{du}{dt}=\left(\left(\frac{ca}{\gamma}-\frac{kc^{2}}{\gamma^{2}}-\frac{\gamma ac-kc^{2}}{\gamma^{2}}\right)+\left(a-\frac{2ck}{\gamma}-\left[\frac{\gamma a-kc}{\gamma}\right]-ku\right)u-\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv\right)</math><math display="block">\frac{du}{dt}=\left(\left(-\frac{kc}{\gamma}-ku\right)u-\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv\right)</math><math display="block">\frac{du}{dt}=-\left(\frac{kc}{\gamma}u+\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv+ku^{2}\right)</math> | |||
E com <math>\dot{y}</math>: | |||
<math display="block">\frac{dy}{dt}=\left(-yc\right)+\left(\gamma yx\right)</math><math display="block">\frac{dv}{dt}=\left(-\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)c\right)+\left(\gamma\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)\left(\frac{c}{\gamma}+u\right)\right)</math><math display="block">\frac{dv}{dt}=\left(-vc-\frac{ac}{\alpha}+\frac{kc^{2}}{\alpha\gamma}\right)+\left(vc+\frac{\gamma ac-kc^{2}}{\alpha\gamma}+\gamma uv+\left[\frac{\gamma a-kc}{\alpha}\right]u\right)</math><math display="block">\frac{dv}{dt}=\gamma uv+\left[\frac{\gamma a-kc}{\alpha}\right]u</math> | |||
Calculando então os limites, relacionado a <math>u</math>: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+ku^{2}}{\frac{kc}{\gamma}u+\frac{c\alpha}{\gamma}v}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+ku^{2}}{u\left(\frac{kc}{\gamma}+\frac{c\alpha}{\gamma}\frac{v}{u}\right)}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha v+ku}{\frac{kc}{\gamma}+\frac{c\alpha}{\gamma}\frac{v}{u}}\right)</math> | |||
E novamente fazendo a substituição <math display="inline">r^{2}=u^{2}+v^{2}</math> e <math display="inline">u=r\cos\theta</math>, <math display="inline">v=r\sin\theta</math>, então: | |||
<math display="block">\lim_{r\rightarrow0}\left(\frac{\alpha r\sin\theta+kr\cos\theta}{\frac{kc}{\gamma}+\frac{c\alpha}{\gamma}\frac{r\sin\theta}{r\cos\theta}}\right)=\lim_{r\rightarrow0}\left(\frac{r\alpha\gamma\sin\theta+rk\gamma\cos\theta}{kc+c\alpha\tan\theta}\right)=0</math> | |||
E a <math>v</math>: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma uv}{\left[\frac{\gamma a-kc}{\alpha}\right]u}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma v}{\left[\frac{\gamma a-kc}{\alpha}\right]}=0</math> | |||
Então os três pontos são semi-lineares. A partir disto, podemos analisar os tipos de estabilidades. Para <math display="inline">\left(0,0\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
a & 0\\ | |||
0 & -c | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)</math> | |||
Então: | |||
<math display="block">\left(a-\lambda\right)\left(c+\lambda\right)=0</math> Novamente temos duas raízes reais de sinais opostos, então temos um ponto de sela, uma instabilidade. Para o segundo ponto: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-a & -\frac{\alpha a}{k}\\ | |||
0 & \gamma\frac{a}{k}-c | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math> | |||
Então: | |||
<math display="block">\left(-a-\lambda\right)\left(\left(\frac{\gamma a}{k}-c\right)-\lambda\right)=0</math><math display="block">\left(a+\lambda\right)\left(\left(\frac{\gamma a}{k}-c\right)-\lambda\right)=0</math> | |||
Temos duas raízes reais uma é negativa <math display="inline">\lambda_{1}=-a</math>. Porém a classificação do ponto depende dos parâmetros escolhidos. Se <math display="inline">\left(\frac{\gamma a}{k}-c\right)>0</math> ou seja <math display="inline">\gamma a>ck</math>, temos uma instabilidade, uma sela, mas se <math display="inline">\gamma a<ck</math>, então temos um nó hiperbólico, ou seja, estabilidade. E por último: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-\frac{kc}{\gamma} & -\frac{c\alpha}{\gamma}\\ | |||
\frac{\gamma a-kc}{\alpha} & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math> | |||
Então: | |||
<math display="block">\left(\frac{kc}{\gamma}+\lambda\right)\lambda+\frac{c\alpha}{\gamma}\left(\frac{\gamma a-kc}{\alpha}\right)=0</math><math display="block">\gamma\lambda^{2}+kc\lambda+c\left(\gamma a-kc\right)=0</math> | |||
Então: | |||
<math display="block">\lambda=-\left(\frac{kc}{2\gamma}\right)\pm\frac{\sqrt{\left(kc\right)^{2}-4\gamma c\left(\gamma a-kc\right)}}{2\gamma}</math><math display="block">\lambda=-\left(\frac{kc}{2\gamma}\right)\pm\frac{\sqrt{\left[\left(kc\right)^{2}+4\gamma c^{2}k\right]-4c\gamma^{2}a}}{2\gamma}</math> | |||
Então o comportamento do sistema vai depender da escolha de parâmetros, porém como todas constantes são positivas <math display="inline">-\left(\frac{kc}{2\gamma}\right)</math> vai ser sempre negativo, e a única forma de ser instável é se <math display="inline">\left(kc\right)^{2}+4\gamma c^{2}k>4c\gamma^{2}a</math>, para garantir que o número seja real, e ainda <math display="inline">\frac{\sqrt{\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a}}{2\gamma}>\frac{kc}{2\gamma}</math> para que o autovalor seja positivo. Analisando então essa última desigualdade: | |||
<math display="block">\frac{\sqrt{\left(kc\right)^{2}+4\gamma c^{2}kc-4c\gamma^{2}a}}{2\gamma}>\frac{kc}{2\gamma}</math><math display="block">\sqrt{\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a}>kc</math> | |||
Elevando ao quadrado: | |||
<math display="block">\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a>\left(kc\right)^{2}</math><math display="block">4\gamma c^{2}k-4c\gamma^{2}a>0</math> | |||
Dividindo por <math display="inline">4c\gamma</math> | |||
<math display="block">ck-\gamma a>0</math><math display="block">ck>\gamma a</math> | |||
Então essa é a condição para que o autovalor seja positivo. E olhando pra primeira desigualdade: | |||
<math display="block">\left(kc\right)^{2}+4\gamma c^{2}k>4c\gamma^{2}a</math><math display="block">\frac{k^{2}c}{4\gamma}+ck>\gamma a</math> | |||
Para garantir que o número seja real. Então temos duas desigualdades para satisfazer para que seja instável: | |||
* <math display="inline">ck>\gamma a</math> | |||
* <math display="inline">\frac{k^{2}c}{4\gamma}+ck>\gamma a</math> | |||
Como <math display="inline">\left(\frac{k^{2}c}{4\gamma}\right)</math> é necessariamente um termo positivo: | |||
<math display="block">\gamma a<ck<\frac{k^{2}c}{4\gamma}+ck</math> | |||
Ou seja, podemos restringir a condição de instabilidade para <math display="inline">ck>\gamma a</math> pois <math display="inline">ck<\frac{k^{2}c}{4\gamma}+ck</math> é uma desigualdade válida para qualquer escolha de parâmetros válidos. Mas lembrando que para o outro ponto é estável se <math display="inline">ck>\gamma a</math> , então sempre temos um ponto de equilíbrio estável e outro instável (além do a instabilidade na origem). Ou seja, por exemplo para valores mais baixos de de <math display="inline">c</math> (termo de crescimento dos predadores) ou <math display="inline">k</math> (termo de amortecimento da presa) temos coexistência de ambas as espécies, se aumentar estes parâmetros, somente a presa sobrevive. Além disso, quando temos <math display="inline">k=0</math>: | |||
<math display="block">\lambda=\pm\frac{\sqrt{-4c\gamma^{2}a}}{2\gamma}=\pm i\sqrt{ca}</math> | |||
Ou seja, temos apenas a parte imaginária, e retornamos à estabilidade do centro. Dessa forma <math display="inline">k=0</math> ou <math display="inline">k\neq0</math> determina se o sistema atinge equilíbrio ou permanece oscilatório, e depois o conjunto de parâmetros, caso atinja estabilidade, determina se ela é atingida com ou sem predadores. | |||
== Exemplo == | |||
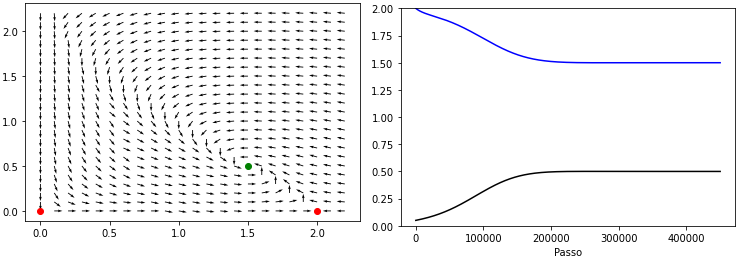
Para estudarmos melhor uma situação, vamos escolher os parâmetros: <math display="inline">a=1</math>, <math display="inline">\alpha=0.5</math>, <math display="inline">k=0.5</math>, <math display="inline">c=0.75</math>,<math display="inline">\gamma=0.5</math>. Então os pontos de equilíbrio são: | |||
*<math display="inline">\left(0,0\right)\rightarrow\lambda=\left\{ 1,-0.75\right\}</math>, uma sela, instável; | |||
*<math display="inline">\left(2,0\right)\rightarrow\lambda=\left\{ -1,0.25\right\}</math>, outro ponto instável, outra sela; | |||
*<math display="inline">\left(1.5,0.5\right)\rightarrow\lambda=\left\{ -0.375+0.22i,-0.375-0.22i\right\}</math>, agora temos um nó assintoticamente estável, pois as parte reais são negativas e as imaginárias são os conjugados. | |||
E fazendo um rascunho do plano de fases, próximo de <math display="inline">\left(0,0\right)</math>, desprezando então os termos não-lineares: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
a & 0\\ | |||
0 & -c | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
1 & 0\\ | |||
0 & -0.75 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{c} | |||
x\\ | |||
-0.75y | |||
\end{array}\right)</math> | |||
Próximo a <math display="inline">\left(\frac{a}{k},0\right)=\left(2,0\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-a & -\frac{\alpha a}{k}\\ | |||
& \gamma\frac{a}{k}-c | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-1 & -1\\ | |||
& 0.25 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-1 & -1\\ | |||
& 0.25 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x-2\\ | |||
y | |||
\end{array}\right)=\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{c} | |||
\left(2-x\right)-y\\ | |||
0.25y | |||
\end{array}\right)</math> | |||
De <math display="inline">\left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)=\left(1.5,0.5\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-\frac{kc}{\gamma} & -\frac{c\alpha}{\gamma}\\ | |||
\frac{\gamma a-kc}{\alpha} & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-0.75 & -0.75\\ | |||
0.25 & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-0.75 & -0.75\\ | |||
0.25 & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x-1.5\\ | |||
y-0.5 | |||
\end{array}\right)=\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{c} | |||
0.75\left[\left(1.5-x\right)+\left(0.5-y\right)\right]\\ | |||
0.25\left(x-1.5\right) | |||
\end{array}\right)</math> | |||
Plotando temos então: | |||
[[Ficheiro:LVA.png|centro|miniaturadaimagem|A esquerda o rascunho do diagrama de fases, e a direita a evolução do sistema para as condições iniciais <math display="inline">\left(x_{0},y_{0}\right)=\left(2,0.05\right)</math>.|741x262px]] | |||
Por curiosidade, se fazemos <math display="inline">k=0</math>: Para <math display="inline">\left(0,0\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
a & 0\\ | |||
0 & -c | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
1 & 0\\ | |||
0 & -0.75 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)</math> | |||
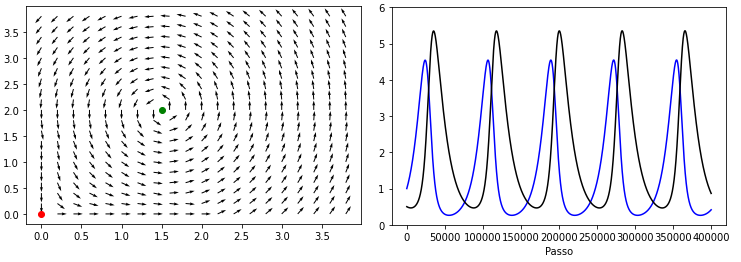
E para <math display="inline">\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)=\left(1.5,2.0\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
0 & -\frac{\alpha c}{\gamma}\\ | |||
\frac{\gamma a}{\alpha} & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
0 & -0.75\\ | |||
1 & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x-1.5\\ | |||
y-2 | |||
\end{array}\right)=\left(\begin{array}{c} | |||
-0.75(y-2)\\ | |||
x-1.5 | |||
\end{array}\right)</math>Plotando o resultado: | |||
[[Ficheiro:LV.png|centro|miniaturadaimagem|A direita o rascunho do diagrama de fase, e a esquerda a evolução para as condições iniciais <math display="inline">\left(x_{0},y_{0}\right)=\left(1,0.5\right)</math>.|741x262px]] | |||
====== Códigos ====== | |||
Os seguintes códigos escritos em Python foram utilizados para obter a solução numérica e plotar o rascunho do diagrama de fases próximo aos pontos de equilíbrio. | |||
<pre> | |||
import matplotlib.pyplot as plt | |||
import numpy as np | |||
# LOTKA-VOLTERRA: Solução numérica | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
def sol_lot(): | |||
x=[] | |||
y=[] | |||
x.append(1) # População inicial de presas | |||
y.append(0.5) # População inicial de predadores | |||
N=400000 # Quantidade de passos | |||
d=0.0001 # Tamanhodos passos | |||
a=0 # 1: Amortecido, 0: Sem amortecimento | |||
for i in range(N-1): | |||
x.append(x[i]+d*(x[i]*(1-0.5*y[i])-0.5*x[i]*x[i]*a)) | |||
y.append(y[i]+d*(y[i]*(-0.75+0.5*x[i]))) | |||
#Plotamos a evolução temporal das frações de população | |||
X=np.arange(len(x)) #Eixo x | |||
plt.plot(X,x,'b-') | |||
plt.plot(X,y,'k-') | |||
plt.xlabel('Passo') | |||
plt.ylim(0,6) | |||
plt.show() | |||
</pre> | |||
A função abaixo tem como finalidade plotar um rascunho do plano de fase próximo ao pontos de equilíbrio do sistema: | |||
<pre> | |||
import matplotlib.pyplot as plt | |||
import numpy as np | |||
# LOTKA-VOLTERRA: Plano de fase | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
def phase_lot(): | |||
X = np.arange(0, 4, 0.2) # Eixo x | |||
Y = np.arange(0, 4, 0.2) # Eixo Y | |||
U,V=np.meshgrid(X,Y) | |||
p1=[0.,0.] # Ponto de equilíbrio 1 | |||
p2=[1.5,2.0] # Ponto de equilíbrio 2 | |||
p3=[1.5*100,0.5*100] # Ponto de equilíbrio 3 | |||
c=0 | |||
for x in X: | |||
l=0 | |||
for y in Y: | |||
#Distâncias | |||
d1=np.sqrt((x-p1[0])*(x-p1[0])+(y-p1[1])*(y-p1[1])) | |||
d2=np.sqrt((x-p2[0])*(x-p2[0])+(y-p2[1])*(y-p2[1])) | |||
d3=np.sqrt((x-p3[0])*(x-p3[0])+(y-p3[1])*(y-p3[1])) | |||
#encontrar o ponto de equilíbrio mais próximo | |||
p=1 | |||
if(d2<d1): | |||
p=2 | |||
if(d3<d2): | |||
p=3 | |||
elif(d3<d1): | |||
p=3 | |||
# Calculamos o vetor de variação do estado baseado no ponto mais próximo: | |||
# [dx/dt,dy/dt]=[a,b] | |||
if(p==1): | |||
a=x | |||
b=-0.75*y | |||
elif(p==2): | |||
a=-0.75*(y-2) | |||
b=x-1.5 | |||
elif(p==3): | |||
a=0.75*((1.5-x)+(0.5-y)) | |||
b=0.25*(x-1.5) | |||
else: | |||
print("Algo deu errado") | |||
m=np.sqrt(a*a+b*b) # Módulo do vetor para normalizar | |||
if(m==0): | |||
m=1 | |||
U[l,c]=a/m | |||
V[l,c]=b/m | |||
l=l+1 | |||
c=c+1 | |||
# Plotamos o resultado | |||
fig, ax = plt.subplots() | |||
ax.quiver(X, Y, U, V) # Os vetores | |||
plt.plot(p1[0],p1[1],'ro') # O ponto de equilíbrio 1 | |||
plt.plot(p2[0],p2[1],'go') # O ponto de equilíbrio 2 | |||
plt.plot(p3[0],p3[1],'go') # O ponto de equilíbrio 3 | |||
plt.show() | |||
</pre> | |||
====== Principais materiais utilizados ====== | |||
# [https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-i-first-order-differential-equations/numerical-methods/ Numerical Methods] (Instituto de Tecnologia de Massachusetts) | |||
# [https://web.mit.edu/10.001/Web/Course_Notes/Differential_Equations_Notes/lec24.html Numerical Solution of Ordinary Differential Equations] (R. Sureshkumar,Instituto de Tecnologia de Massachusetts) | |||
# A estes materiais, somam-se os vistos em [[Modelo de Lotka-Volterra]] | |||
====== Citações ====== | |||
<references /> | |||
{{Ecologia| [[Modelo de Lotka-Volterra]] |[[Modelo de Levins aprimorado para 2 espécies | Modelo de Levins aprimorado para 2 espécies I]]}} | |||
Edição atual tal como às 17h44min de 2 de maio de 2021
Anterior: Modelo de Lotka-Volterra | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies I
Uma versão do modelo de Lotka-Volterra aprimorada inclui um termo de saturação na população de presas, isto é, um termo logístico (que inibe o aumento exponencial) visando representar a finitude dos recursos disponíveis para uma espécie. Este modelo é chamado de modelo de Lotka-Volterra amortecido.
Onde é uma constante positiva. Agora temos três pontos de equilíbrio, novamente temos . Mas temos outro ponto quando apenas :
Então ou seja um ponto de equilíbrio com apenas a sobrevivência da presa. E ainda temos também um ponto de coexistência entre ambas as espécies:
Isolando então na segunda equação e substituindo na primeira:
Então nosso outro ponto de equilíbrio é dado por. Infelizmente as equações não são separáveis como no caso anterior, portanto vamos analisar se a equação é semi-linear nas proximidades dos pontos de equilíbrio. Para :
Para e fazendo a mudança de variáveis , e , temos:
E:
Então:
Podemos fazer uma substituição de variável novamente usando coordenadas polares[1] e , , então:
E o limite:
E por fim, vamos estudar os pontos de estabilidade em torno de , tendo agora e , então, manipulando novamente, primeiro trabalhando com :
E com :
Calculando então os limites, relacionado a :
E novamente fazendo a substituição e , , então:
E a :
Então os três pontos são semi-lineares. A partir disto, podemos analisar os tipos de estabilidades. Para :
Então:
Então:
Temos duas raízes reais uma é negativa . Porém a classificação do ponto depende dos parâmetros escolhidos. Se ou seja , temos uma instabilidade, uma sela, mas se , então temos um nó hiperbólico, ou seja, estabilidade. E por último:
Então:
Então:
Então o comportamento do sistema vai depender da escolha de parâmetros, porém como todas constantes são positivas vai ser sempre negativo, e a única forma de ser instável é se , para garantir que o número seja real, e ainda para que o autovalor seja positivo. Analisando então essa última desigualdade:
Elevando ao quadrado:
Dividindo por
Então essa é a condição para que o autovalor seja positivo. E olhando pra primeira desigualdade:
Para garantir que o número seja real. Então temos duas desigualdades para satisfazer para que seja instável:
Como é necessariamente um termo positivo:
Ou seja, podemos restringir a condição de instabilidade para pois é uma desigualdade válida para qualquer escolha de parâmetros válidos. Mas lembrando que para o outro ponto é estável se , então sempre temos um ponto de equilíbrio estável e outro instável (além do a instabilidade na origem). Ou seja, por exemplo para valores mais baixos de de (termo de crescimento dos predadores) ou (termo de amortecimento da presa) temos coexistência de ambas as espécies, se aumentar estes parâmetros, somente a presa sobrevive. Além disso, quando temos :
Ou seja, temos apenas a parte imaginária, e retornamos à estabilidade do centro. Dessa forma ou determina se o sistema atinge equilíbrio ou permanece oscilatório, e depois o conjunto de parâmetros, caso atinja estabilidade, determina se ela é atingida com ou sem predadores.
Exemplo
Para estudarmos melhor uma situação, vamos escolher os parâmetros: , , , ,. Então os pontos de equilíbrio são:
- , uma sela, instável;
- , outro ponto instável, outra sela;
- , agora temos um nó assintoticamente estável, pois as parte reais são negativas e as imaginárias são os conjugados.
E fazendo um rascunho do plano de fases, próximo de , desprezando então os termos não-lineares:
Próximo a :
De :
Plotando temos então:
Por curiosidade, se fazemos : Para :
E para :
Códigos
Os seguintes códigos escritos em Python foram utilizados para obter a solução numérica e plotar o rascunho do diagrama de fases próximo aos pontos de equilíbrio.
import matplotlib.pyplot as plt
import numpy as np
# LOTKA-VOLTERRA: Solução numérica
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
def sol_lot():
x=[]
y=[]
x.append(1) # População inicial de presas
y.append(0.5) # População inicial de predadores
N=400000 # Quantidade de passos
d=0.0001 # Tamanhodos passos
a=0 # 1: Amortecido, 0: Sem amortecimento
for i in range(N-1):
x.append(x[i]+d*(x[i]*(1-0.5*y[i])-0.5*x[i]*x[i]*a))
y.append(y[i]+d*(y[i]*(-0.75+0.5*x[i])))
#Plotamos a evolução temporal das frações de população
X=np.arange(len(x)) #Eixo x
plt.plot(X,x,'b-')
plt.plot(X,y,'k-')
plt.xlabel('Passo')
plt.ylim(0,6)
plt.show()
A função abaixo tem como finalidade plotar um rascunho do plano de fase próximo ao pontos de equilíbrio do sistema:
import matplotlib.pyplot as plt
import numpy as np
# LOTKA-VOLTERRA: Plano de fase
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
def phase_lot():
X = np.arange(0, 4, 0.2) # Eixo x
Y = np.arange(0, 4, 0.2) # Eixo Y
U,V=np.meshgrid(X,Y)
p1=[0.,0.] # Ponto de equilíbrio 1
p2=[1.5,2.0] # Ponto de equilíbrio 2
p3=[1.5*100,0.5*100] # Ponto de equilíbrio 3
c=0
for x in X:
l=0
for y in Y:
#Distâncias
d1=np.sqrt((x-p1[0])*(x-p1[0])+(y-p1[1])*(y-p1[1]))
d2=np.sqrt((x-p2[0])*(x-p2[0])+(y-p2[1])*(y-p2[1]))
d3=np.sqrt((x-p3[0])*(x-p3[0])+(y-p3[1])*(y-p3[1]))
#encontrar o ponto de equilíbrio mais próximo
p=1
if(d2<d1):
p=2
if(d3<d2):
p=3
elif(d3<d1):
p=3
# Calculamos o vetor de variação do estado baseado no ponto mais próximo:
# [dx/dt,dy/dt]=[a,b]
if(p==1):
a=x
b=-0.75*y
elif(p==2):
a=-0.75*(y-2)
b=x-1.5
elif(p==3):
a=0.75*((1.5-x)+(0.5-y))
b=0.25*(x-1.5)
else:
print("Algo deu errado")
m=np.sqrt(a*a+b*b) # Módulo do vetor para normalizar
if(m==0):
m=1
U[l,c]=a/m
V[l,c]=b/m
l=l+1
c=c+1
# Plotamos o resultado
fig, ax = plt.subplots()
ax.quiver(X, Y, U, V) # Os vetores
plt.plot(p1[0],p1[1],'ro') # O ponto de equilíbrio 1
plt.plot(p2[0],p2[1],'go') # O ponto de equilíbrio 2
plt.plot(p3[0],p3[1],'go') # O ponto de equilíbrio 3
plt.show()
Principais materiais utilizados
- Numerical Methods (Instituto de Tecnologia de Massachusetts)
- Numerical Solution of Ordinary Differential Equations (R. Sureshkumar,Instituto de Tecnologia de Massachusetts)
- A estes materiais, somam-se os vistos em Modelo de Lotka-Volterra
Citações
- ↑ Limits and Continuity (Rebecca Noonan-Heale ,Universidade de Utah)
Anterior: Modelo de Lotka-Volterra | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies I

































![{\displaystyle {\frac {du}{dt}}=\left({\frac {ca}{\gamma }}+au-{\frac {kc^{2}}{\gamma ^{2}}}-ku^{2}-{\frac {2ck}{\gamma }}u\right)-\left({\frac {c\alpha }{\gamma }}v+{\frac {\gamma ac-kc^{2}}{\gamma ^{2}}}+\alpha uv+\left[{\frac {\gamma a-kc}{\gamma }}\right]u\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1420f662c6a6ee776530039c25a882218132a23)
![{\displaystyle {\frac {du}{dt}}=\left(\left({\frac {ca}{\gamma }}-{\frac {kc^{2}}{\gamma ^{2}}}-{\frac {\gamma ac-kc^{2}}{\gamma ^{2}}}\right)+\left(a-{\frac {2ck}{\gamma }}-\left[{\frac {\gamma a-kc}{\gamma }}\right]-ku\right)u-{\frac {c\alpha }{\gamma }}v\right)-\left(\alpha uv\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1ae4d7cdf9852db3ffe06e2abceee2145cc6581)





![{\displaystyle {\frac {dv}{dt}}=\left(-vc-{\frac {ac}{\alpha }}+{\frac {kc^{2}}{\alpha \gamma }}\right)+\left(vc+{\frac {\gamma ac-kc^{2}}{\alpha \gamma }}+\gamma uv+\left[{\frac {\gamma a-kc}{\alpha }}\right]u\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d677c67a4874a279b2d3f38cb24ffe0a77dd536)
![{\displaystyle {\frac {dv}{dt}}=\gamma uv+\left[{\frac {\gamma a-kc}{\alpha }}\right]u}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73c5d6a722a8e4fd4afe1bb2536b92cb8f6b345f)




![{\displaystyle \lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma uv}{\left[{\frac {\gamma a-kc}{\alpha }}\right]u}}=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma v}{\left[{\frac {\gamma a-kc}{\alpha }}\right]}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96e69b5a4e9cb6d6848f846bd70accd7415d9d92)













![{\displaystyle \lambda =-\left({\frac {kc}{2\gamma }}\right)\pm {\frac {\sqrt {\left[\left(kc\right)^{2}+4\gamma c^{2}k\right]-4c\gamma ^{2}a}}{2\gamma }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f8472edff452cee5ba5c30e982c5f418ab9bef)





































![{\displaystyle \left({\begin{array}{c}{\dot {x}}\\{\dot {y}}\end{array}}\right)=\left({\begin{array}{c}0.75\left[\left(1.5-x\right)+\left(0.5-y\right)\right]\\0.25\left(x-1.5\right)\end{array}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a0b0d8fa8ca91b22327eab2aac0153fd471d1d8)