Modelo de Lotka-Volterra: mudanças entre as edições
(Limpou toda a página) |
|||
| (9 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[AC: Jogo da Vida | Jogo da Vida]]|[[Modelo de Lotka-Volterra amortecido]]}} | |||
== Versão tradicional == | |||
No modelo de Lotka-Volterra temos as seguintes considerações: | |||
*Na ausência de predadores, a população de presas aumenta a uma taxa proporcional à população atual; | |||
*Na ausência de presas, os predadores irão à extinção; | |||
*O número de encontro entre presas e predadores é proporcional a produto das duas populações. | |||
**Estes encontros beneficiam os predadores em detrimento das presas. | |||
Dessa forma, as equações são: | |||
*<math display="inline">\frac{dx}{dt}=x\left(a-\alpha y\right)</math> | |||
*<math display="inline">\frac{dy}{dt}=y\left(-c+\gamma x\right)</math> | |||
Onde: | |||
*<math display="inline">a:</math> taxa de crescimento de presas sem predadores; | |||
*<math display="inline">\alpha:</math>taxa de decréscimo da população de presas devido a predação; | |||
*<math display="inline">c:</math> taxa de mortalidade da população de predadores sem presas; | |||
*'''<math display="inline">\gamma</math>''': taxa de crescimento de predadores devido a predação. | |||
=== Separação de variáveis === | |||
Utilizando a separação de variáveis, temos: | |||
<math display="block">\frac{dy}{dt}\frac{dt}{dx}=\frac{y\left(-c+\gamma x\right)}{x\left(a-\alpha y\right)}</math> | |||
Logo: | |||
<math display="block">\frac{dy}{dx}=\frac{y\left(-c+\gamma x\right)}{x\left(a-\alpha y\right)}</math><math display="block">\frac{\left(a-\alpha y\right)}{y}dy=\frac{\left(-c+\gamma x\right)}{x}dx</math><math display="block">\left(\frac{a}{y}-\alpha\right)dy=\left(-\frac{c}{x}+\gamma\right)dx</math>Integrando ambos os lados: | |||
<math display="block">a\ln y-\alpha y=-c\ln x+\gamma x+C</math><math display="block">a\ln y-\alpha y+c\ln x-\gamma x=C</math> | |||
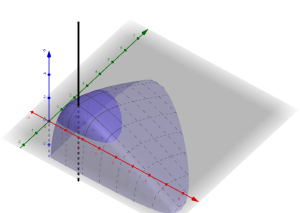
Onde <math display="inline">C</math> é uma constante de integração. Para plotarmos um gráfico, considerando apenas <math display="inline">a=\alpha=\gamma=c=1</math> Temos então: | |||
<math display="block">\ln y+\ln x-\left(x+y\right)=C</math> | |||
Um ponto de equilíbrio fora da origem é obtido quando: | |||
<math display="block">\frac{dx}{dt}=x\left(a-\alpha y\right)=0\rightarrow y=\frac{a}{\alpha}=1</math><math display="block">\frac{dy}{dt}=y\left(-c+\gamma x\right)=0\rightarrow x=\frac{c}{\gamma}=1</math> | |||
Então neste caso, o sistema oscila em torno de <math display="inline">\left(1,1\right)</math> e a constante <math display="inline">C</math> é definida pelas condições iniciais <math display="inline">\left(x_{0},y_{0}\right)</math>. Para a condição em que <math display="inline">x_{0}=y_{0}=1</math>, então: | |||
<math display="block">\ln1+\ln1-\left(1+1\right)=C</math><math display="block">-2=C</math> | |||
Então para este conjunto de parâmetros e condições iniciais: <math display="block">\ln y+\ln x-\left(x+y\right)+2=0</math> | |||
Neste caso o sistema vai permanecer no ponto de equilíbrio. Para outras condições iniciais, o sistema vai oscilar em torno do ponto de equilíbrio. Obviamente além do ponto <math display="inline">\left(1,1\right)</math>, temos um ponto de equilíbrio em <math display="inline">\left(0,0\right)</math>. Vamos analisar a dinâmica na vizinhança dos pontos através de um processo simples de linearização. | |||
[[Ficheiro:Plot Lotka-Volterra.png|borda|miniaturadaimagem|<math>f\left(x,y\right)=\ln y+\ln x-\left(x+y\right)-C</math> com as condições <math>a=\alpha=c=\gamma=1</math> e condição inicial arbitrária, plotado no [https://www.geogebra.org/ GeoGebra].|alt=]] | |||
=== Linearização em torno do ponto de equilíbrio === | |||
Primeiro podemos perceber que o sistema é quase-linear em torno de <math display="inline">\left(0,0\right)</math>, verificando que satisfaz: | |||
<math display="block">\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}\left[\frac{\text{parte não linear}}{\text{parte linear}}\right]=0</math> | |||
Então lembrando as equações: | |||
*<math display="inline">\frac{dx}{dt}=\left[xa\right]-\left(\alpha xy\right)=\left[\text{linear}\right]-\left(\text{não linear}\right)</math> | |||
*<math display="inline">\frac{dy}{dt}=-\left[yc\right]+\left(\gamma yx\right)=-\left[\text{linear}\right]+\left(\text{não linear}\right)</math> | |||
Logo: | |||
<math display="block">\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha xy}{xa}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha}{a}y=0</math><math display="block">\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma xy}{cy}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}x=0</math> | |||
Desprezando então os termos não lineares podemos escrever o seguinte sistema linearizado em torno da origem: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
a & 0\\ | |||
0 & -c | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)</math>Calculando os autovalores da matriz, obtemos então: | |||
<math display="block">-\left(a-\lambda\right)\left(-c-\lambda\right)=0</math><math display="block">\left(a-\lambda\right)\left(c+\lambda\right)=0</math> | |||
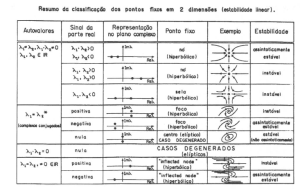
os seguintes autovalores <math display="inline">\lambda=\left\{ a,-c\right\}</math>. Como um dos valores tem parte real positiva, então é um ponto instável, especificamente devido aos sinais opostos é um ponto de sela. Como é instável significa que se a condição inicial for próxima de <math display="inline">\left(0,0\right)</math>, a evolução do sistema vai se afastar do ponto de equilíbrio. Essa aproximação também indica que próximo do ponto de equilíbrio, a dinâmica pode ser descrita tanto pelo conjunto de equações não lineares, como pelo sistema linear. | |||
Agora o segundo ponto de equilíbrio, de maneira geral é <math display="inline">\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)</math>. Primeiro reescrevemos o sistema em torno do ponto de equilíbrio, isto é, fazemos um deslocamento <math display="inline">u=x-\frac{c}{\gamma}</math> e <math display="inline">v=y-\frac{a}{\alpha}</math>. Então temos <math display="inline">dx=du</math> e <math display="inline">dv=dy</math> e substituindo, para <math display="inline">\dot{x}</math>:<math display="block">\frac{du}{dt}=\left(u+\frac{c}{\gamma}\right)a-\alpha\left(u+\frac{c}{\gamma}\right)\left(v+\frac{a}{\alpha}\right)</math><math display="block">\frac{du}{dt}=ua+\frac{c}{\gamma}a-\alpha uv-\frac{\alpha c}{\gamma}v-ua-\frac{ca}{\gamma}</math><math display="block">\frac{du}{dt}=-\alpha uv-\frac{\alpha c}{\gamma}v</math>E para <math display="inline">\dot{y}</math>: | |||
<math display="block">\frac{dv}{dt}=-\left(v+\frac{a}{\alpha}\right)c+\gamma\left(v+\frac{a}{\alpha}\right)\left(u+\frac{c}{\gamma}\right)</math><math display="block">\frac{dv}{dt}=-cv-\frac{ca}{\alpha}+\gamma vu+\frac{\gamma a}{\alpha}u+cv+\frac{ca}{\alpha}</math><math display="block">\frac{dv}{dt}=\gamma vu+\frac{\gamma a}{\alpha}u</math>Podemos analisar o comportamento em torno do ponto de equilíbrio: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}-\frac{\alpha uv}{\frac{\alpha vc}{\gamma}}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}u=0</math><math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma vu}{\frac{\gamma au}{\alpha}}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\alpha}{a}v=0</math>Desprezando os termos não lineares então: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
0 & -\frac{\alpha c}{\gamma}\\ | |||
\frac{\gamma a}{\alpha} & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math>Então os autovalores correspondentes: | |||
<math display="block">-\lambda^{2}-\frac{\gamma a}{\alpha}\frac{\alpha c}{\gamma}=0</math><math display="block">\lambda=\pm\sqrt{-ac}=\pm\sqrt{ac}i</math> | |||
Como temos raízes puramente imaginárias e <math display="inline">\lambda_{1}=\lambda_{2}^{*}</math>, temos um centro, ponto de estabilidade. Isto é, se a condição inicial for próxima de <math display="inline">\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)</math> o sistema evoluirá de forma que o estado do sistema permanecerá próximo do ponto de equilíbrio. | |||
<div class="center">[[Ficheiro:Tabela de autovaloes.png|miniaturadaimagem|Classificação dos pontos de estabilidade de acordo com os autovalores<ref>[http://www.sel.eesc.usp.br/lac/disciplinas/sels/arquivos/sel364/private/aula1a2cnl.pdf Análise de sistemas não-lineares] (Vilma A. Oliveira e José Ricardo Rosolen, USP)</ref>.|300x300px]]</div> | |||
=== Segundo método de Lyapunov === | |||
Para avaliar o ponto <math display="inline">\left(x_{1},y_{1}\right)=\left(0,0\right)</math>, podemos usar de maneira análoga ao [[Métodos de Lyapunov|exemplo do segundo critério de Lyapunov]]: | |||
<math display="block">V\left(\boldsymbol{x}\right)=\frac{x^{2}}{\alpha}-\frac{y^{2}}{\gamma}</math> | |||
Como já discutimos <math display="inline">V\left(\boldsymbol{x}_{0}\right)=0</math> e a região <math display="inline">W^{+}\left\{ \left(x,y\right)|\left|x\right|>\left|y\right|\right\}</math> onde <math display="inline">V\left(\boldsymbol{x}\right)>0</math> para <math display="inline">\boldsymbol{x}\neq\boldsymbol{x}_{0}</math> , sendo <math display="inline">\boldsymbol{x}_{0}</math> um ponto de acumulação em <math display="inline">W^{+}</math><ref>[http://www.dii.unimo.it/~zanasi/didattica/Teoria_dei_Sistemi/Luc_TDS_ING_2016_Stability_Analysis_of_Nonlinear_Systems.pdf Stability Analysis of Nonlinear Systems] (Roberto Zanasi, Universidade de Módena e Reggio Emília)</ref>. Então: | |||
<math display="block">\begin{align} | |||
\dot{V}\left(\boldsymbol{x}\right) & =\left[\nabla V\right]\cdot\left[\boldsymbol{f}\left(\boldsymbol{x}\right)\right]\\ | |||
& =\left(\frac{2x}{\alpha},-\frac{2y}{\gamma}\right)\left(\dot{x},\dot{y}\right)\\ | |||
& =2x^{2}\frac{a}{\alpha}-2x^{2}y+2y^{2}\frac{c}{\gamma}-2y^{2}x\\ | |||
& =2x^{2}\left(\frac{a}{\alpha}-y\right)+2y^{2}\left(\frac{c}{\gamma}-x\right)\end{align}</math>Lembrando do nosso segundo ponto de equilíbrio <math display="inline">\left(x_{2},y_{2}\right)=\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)</math>: | |||
<math display="block">\dot{V}\left(\boldsymbol{x}\right)=2x^{2}\left(y_{2}-y\right)+2y^{2}\left(x_{2}-x\right)</math> | |||
Então se estamos próximos suficiente do ponto de equilíbrio em análise <math display="inline">\left(x_{1},y_{1}\right)=\left(0,0\right)</math>, temos então uma instabilidade local pois <math display="inline">\dot{V}\left(\boldsymbol{x}\right)>0</math> é positivo definido em <math display="inline">W^{+}</math>, uma vez que <math display="inline">\left|y\right|<\left|y_{2}\right|</math> , <math display="inline">\left|x\right|<\left|x_{2}\right|</math>. Olhando o segundo ponto de equilíbrio, <math display="inline">\left(x_{2},y_{2}\right)=\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)</math>, podemos manipular as equações da seguinte forma: | |||
*<math display="inline">\frac{dx}{dt}=x\left(a-\alpha y\right)=x\alpha\left(\frac{a}{\alpha}-y\right)=x\alpha\left(y_{2}-y\right)</math> | |||
*<math display="inline">\frac{dy}{dt}=y\left(-c+\gamma x\right)=y\gamma\left(-\frac{c}{\gamma}+x\right)=y\gamma\left(-x_{2}+x\right)</math> | |||
Definindo então a seguinte função de Lyapunov: | |||
<math display="block">V\left(x,y\right)=x-x_{2}\left[1+\ln\left(\frac{x}{x_{2}}\right)\right]+\frac{\alpha}{\gamma}\left(y-y_{2}\left[1+\ln\left(\frac{y}{y_{2}}\right)\right]\right)</math> | |||
Analisando no ponto de e equilíbrio, temos: | |||
<math display="block">\begin{align} | |||
V\left(x_{2},y_{2}\right) & =x_{2}-x_{2}\left[1+\ln\left(\frac{x_{2}}{x_{2}}\right)\right]+\frac{\alpha}{\gamma}\left(y_{2}-y_{2}\left[1+\ln\left(\frac{y_{2}}{y_{2}}\right)\right]\right)\\ | |||
& =x_{2}-x_{2}+\frac{\alpha}{\gamma}\left(y_{2}-y_{2}\right)\\ | |||
& =0\end{align}</math> | |||
Agora precisamos que para <math display="inline">\left(x,y\right)\neq0</math> tenhamos <math display="inline">V>0</math>, na região próxima ao ponto de equilíbrio. Separando em dois termos: | |||
<math display="block">\begin{align} | |||
V\left(x,y\right) & =\left[x-x_{2}\left(1+\ln\left(\frac{x}{x_{2}}\right)\right)\right]+\frac{\alpha}{\gamma}\left[y-y_{2}\left(1+\ln\left(\frac{y}{y_{2}}\right)\right)\right]\\ | |||
& =V\left(x\right)+\frac{\alpha}{\gamma}V\left(y\right)\end{align}</math> | |||
De forma geral temos <math display="inline">V\left(z\right)=z-z_{2}\left(1+\ln\left(\frac{z}{z_{2}}\right)\right)</math>, e precisamos que <math display="inline">V\left(z\right)>0</math> quando <math display="inline">z\neq z_{2}</math>. Além de ser facilmente visto via gráfico para todos os valores aceitáveis <math display="inline">z,z_{2}\in\left[0,1\right]</math>, também podemos analisar a seguinte desigualdade: | |||
<math display="block">\begin{align} | |||
z-z_{2}\left(1+\ln\left(\frac{z}{z_{2}}\right)\right) & >0\\ | |||
z & >z_{2}\left(1+\ln\left(\frac{z}{z_{2}}\right)\right)\\ | |||
\frac{z}{z_{2}} & >1+\ln\left(\frac{z}{z_{2}}\right)\\ | |||
e^{\frac{z}{z_{2}}} & >e\frac{z}{z_{2}}\\ | |||
e^{u} & >eu\end{align}</math>Podemos ver quer a desigualdade desigualdade é válida exceto se <math display="inline">x=1</math>. Mas como fizemos a seguinte substituição <math display="inline">u=\frac{z}{z_{2}}</math> então <math display="inline">u=1\rightarrow z=z_{2}</math>, e de fato que queremos que seja positiva definida fora do ponto de equilíbrio. Uma vez que sabemos que <math display="inline">V\left(x,y\right)</math> é positivo definido, calculamos então: | |||
<math display="block">\begin{align} | |||
\dot{V}\left(\boldsymbol{x}\right) & =\left[\nabla V\right]\cdot\left[\boldsymbol{f}\left(\boldsymbol{x}\right)\right]\\ | |||
& =\left[\frac{\partial V\left(x\right)}{\partial x},\frac{\alpha}{\gamma}\frac{\partial V\left(y\right)}{\partial y}\right]\cdot\left[x\alpha\left(y_{2}-y\right),y\gamma\left(-x_{2}+x\right)\right] \\ | |||
& =\left[1-\frac{x_{2}}{x},\frac{\alpha}{\gamma}\left(1-\frac{y_{2}}{y}\right)\right]\cdot\left[x\alpha\left(y_{2}-y\right),y\gamma\left(-x_{2}+x\right)\right]\\ | |||
& =\left(\frac{x-x_{2}}{x}\right)\left(x\alpha\left(y_{2}-y\right)\right)+\frac{\alpha}{\gamma}\left(\frac{y-y_{2}}{y}\right)\left(y\gamma\left(-x_{2}+x\right)\right)\end{align}</math> | |||
Então:<math display="block">\dot{V}\left(\boldsymbol{x}\right)=\alpha\left(x-x_{2}\right)\left(y_{2}-y\right)-\alpha\left(y_{2}-y\right)\left(x-x_{2}\right)=0</math>Temos então a condição de estabilidade <math display="inline">\dot{V}\leq0</math> concordando como que já havíamos obtidos anteriormente. | |||
=== Solução numérica === | |||
Um exemplo resolvido numericamente pode ser visto em [[Modelo de Lotka-Volterra amortecido]], onde foi aproveitado os códigos desenvolvidos para este mesmo. | |||
== Versão adimensional == | |||
Originalmente temos 4 parâmetros, mas podemos realizar uma série de manipulações visando uma redução da quantidade de parâmetros. Escrevendo o sistema como: | |||
<math display="block">\begin{align} | |||
\frac{dN}{dt} & =aN-bNP\\ | |||
\frac{dP}{dt} & =cPN-dP | |||
\end{align}</math> | |||
Podemos definir então <math display="inline">\widehat{t}=at</math>. Multiplicando ambas equações por <math display="inline">1/a</math>: | |||
<math display="block">\begin{align} | |||
\frac{1}{a}\frac{dN}{dt} & =N-\frac{b}{a}NP\\ | |||
\frac{1}{a}\frac{dP}{dt} & =\frac{c}{a}PN-\frac{d}{a}P | |||
\end{align}</math> | |||
Se definimos <math display="inline">p=\left(b/a\right)P</math> e multiplicamos a segunda equação por <math display="inline">b/a</math>: | |||
<math display="block">\begin{align} | |||
\frac{dN}{d\widehat{t}} & =N-Np\\ | |||
\frac{d}{d\widehat{t}}\left(\frac{bP}{a}\right) & =\frac{c}{a}\left(\frac{b}{a}P\right)N-\frac{d}{a}\left(\frac{b}{a}P\right) | |||
\end{align}</math> | |||
Agora se multiplicamos a primeira linha e definimos <math display="inline">n=\left(c/d\right)N</math>: | |||
<math display="block">\begin{align} | |||
\frac{d}{d\widehat{t}}\left(\frac{c}{d}N\right) & =\frac{c}{d}N-\left(\frac{c}{d}N\right)p\\ | |||
\frac{dp}{d\widehat{t}} & =\frac{c}{a}pN-\frac{d}{a}p | |||
\end{align}</math> | |||
Definindo então <math display="inline">\alpha=\frac{d}{a}</math>: | |||
<math display="block">\begin{align} | |||
\frac{d n}{d\widehat{t}} & =n-np\\ | |||
\frac{dp}{d\widehat{t}} & =\frac{c}{a}\frac{d}{c}pn-\alpha p | |||
\end{align}</math> | |||
Ou então, ficamos apenas com um único parâmetro. | |||
<math display="block">\begin{align} | |||
\frac{dn}{d\widehat{t}} & =n\left(1-p\right)\\ | |||
\frac{dp}{d\widehat{t}} & =\alpha p\left(n-1\right) | |||
\end{align}</math> | |||
=== Separação de variáveis === | |||
Aplicando a separação de variáveis, temos então: <math display="block">\begin{align} | |||
\frac{dp}{dn} & =\frac{\alpha p\left(n-1\right)}{n\left(1-p\right)}\\ | |||
\frac{\left(1-p\right)}{p}dp & =\alpha\frac{\left(n-1\right)}{n}dn\\ | |||
\left(\frac{1}{p}-1\right)dp & =\alpha\left(1-\frac{1}{n}\right)dn\\ | |||
\ln p-p+K & =\alpha\left(n-\ln\left(n\right)\right)\\ | |||
K & =\alpha n+p-\alpha\ln\left(n\right)-\ln p | |||
\end{align}</math> | |||
Ou ainda, apenas: | |||
<math display="block">K=\alpha n+p+\ln\left(n^{\alpha}p\right)</math> | |||
== Referências == | |||
=== Principais materiais utilizados === | |||
# [http://www.math.nthu.edu.tw/~sbhsu/0416.pdf A survey of constructing Lyapunov functions for mathematical models in population biology] (Sze-Bi, Revista Taiwanesa de Matemática ) | |||
# [https://repositorio.unesp.br/bitstream/handle/11449/134026/000856864.pdf?sequence=1||Estabilidade Estabilidade de pontos de equilíbrio e existência de soluções periódicas em alguns modelos bidimensionais] (Salvador Tavares de Oliveira, UNESP) | |||
# [https://arxiv.org/ftp/arxiv/papers/1504/1504.06244.pdf||Modelagem Modelagem Matemática e estabilidade de sistemas predador-presa] (Paulo Laerte Natti e outros, UEL) | |||
# [https://guri.unipampa.edu.br/uploads/evt/arq_trabalhos/12356/seer_12356.pdf||Modelo Modelo de Lotka-Volterra: a dinâmica predador-presa] (Rafael Biasi Pata e Elisa Regina Cara, UNIPAMPA) | |||
=== Citações === | |||
<references /> | |||
{{Ecologia| [[AC: Jogo da Vida | Jogo da Vida]]|[[Modelo de Lotka-Volterra amortecido]]}} | |||
Edição atual tal como às 00h42min de 10 de novembro de 2022
Anterior: Jogo da Vida | Índice: Ecologia | Próximo: Modelo de Lotka-Volterra amortecido
Versão tradicional
No modelo de Lotka-Volterra temos as seguintes considerações:
- Na ausência de predadores, a população de presas aumenta a uma taxa proporcional à população atual;
- Na ausência de presas, os predadores irão à extinção;
- O número de encontro entre presas e predadores é proporcional a produto das duas populações.
- Estes encontros beneficiam os predadores em detrimento das presas.
Dessa forma, as equações são:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dx}{dt}=x\left(a-\alpha y\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dy}{dt}=y\left(-c+\gamma x\right)}
Onde:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle a:} taxa de crescimento de presas sem predadores;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha:} taxa de decréscimo da população de presas devido a predação;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c:} taxa de mortalidade da população de predadores sem presas;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \gamma} : taxa de crescimento de predadores devido a predação.
Separação de variáveis
Utilizando a separação de variáveis, temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}\frac{dt}{dx}=\frac{y\left(-c+\gamma x\right)}{x\left(a-\alpha y\right)}}
Logo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dx}=\frac{y\left(-c+\gamma x\right)}{x\left(a-\alpha y\right)}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\left(a-\alpha y\right)}{y}dy=\frac{\left(-c+\gamma x\right)}{x}dx} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{a}{y}-\alpha\right)dy=\left(-\frac{c}{x}+\gamma\right)dx} Integrando ambos os lados:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\ln y-\alpha y=-c\ln x+\gamma x+C} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\ln y-\alpha y+c\ln x-\gamma x=C}
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle C} é uma constante de integração. Para plotarmos um gráfico, considerando apenas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle a=\alpha=\gamma=c=1} Temos então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln y+\ln x-\left(x+y\right)=C}
Um ponto de equilíbrio fora da origem é obtido quando:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=x\left(a-\alpha y\right)=0\rightarrow y=\frac{a}{\alpha}=1} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}=y\left(-c+\gamma x\right)=0\rightarrow x=\frac{c}{\gamma}=1}
Então neste caso, o sistema oscila em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(1,1\right)} e a constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle C} é definida pelas condições iniciais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{0},y_{0}\right)} . Para a condição em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{0}=y_{0}=1} , então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln1+\ln1-\left(1+1\right)=C} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2=C}
Então para este conjunto de parâmetros e condições iniciais: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln y+\ln x-\left(x+y\right)+2=0}
Neste caso o sistema vai permanecer no ponto de equilíbrio. Para outras condições iniciais, o sistema vai oscilar em torno do ponto de equilíbrio. Obviamente além do ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(1,1\right)} , temos um ponto de equilíbrio em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} . Vamos analisar a dinâmica na vizinhança dos pontos através de um processo simples de linearização.
Linearização em torno do ponto de equilíbrio
Primeiro podemos perceber que o sistema é quase-linear em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} , verificando que satisfaz:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}\left[\frac{\text{parte não linear}}{\text{parte linear}}\right]=0}
Então lembrando as equações:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dx}{dt}=\left[xa\right]-\left(\alpha xy\right)=\left[\text{linear}\right]-\left(\text{não linear}\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dy}{dt}=-\left[yc\right]+\left(\gamma yx\right)=-\left[\text{linear}\right]+\left(\text{não linear}\right)}
Logo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha xy}{xa}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha}{a}y=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma xy}{cy}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}x=0}
Desprezando então os termos não lineares podemos escrever o seguinte sistema linearizado em torno da origem:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} a & 0\\ 0 & -c \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)} Calculando os autovalores da matriz, obtemos então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\left(a-\lambda\right)\left(-c-\lambda\right)=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(a-\lambda\right)\left(c+\lambda\right)=0}
os seguintes autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda=\left\{ a,-c\right\}}
. Como um dos valores tem parte real positiva, então é um ponto instável, especificamente devido aos sinais opostos é um ponto de sela. Como é instável significa que se a condição inicial for próxima de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)}
, a evolução do sistema vai se afastar do ponto de equilíbrio. Essa aproximação também indica que próximo do ponto de equilíbrio, a dinâmica pode ser descrita tanto pelo conjunto de equações não lineares, como pelo sistema linear.
Agora o segundo ponto de equilíbrio, de maneira geral é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{a}{\alpha}\right)} . Primeiro reescrevemos o sistema em torno do ponto de equilíbrio, isto é, fazemos um deslocamento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=x-\frac{c}{\gamma}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v=y-\frac{a}{\alpha}} . Então temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle dx=du} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle dv=dy} e substituindo, para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{x}} :Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left(u+\frac{c}{\gamma}\right)a-\alpha\left(u+\frac{c}{\gamma}\right)\left(v+\frac{a}{\alpha}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=ua+\frac{c}{\gamma}a-\alpha uv-\frac{\alpha c}{\gamma}v-ua-\frac{ca}{\gamma}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=-\alpha uv-\frac{\alpha c}{\gamma}v} E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{y}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=-\left(v+\frac{a}{\alpha}\right)c+\gamma\left(v+\frac{a}{\alpha}\right)\left(u+\frac{c}{\gamma}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=-cv-\frac{ca}{\alpha}+\gamma vu+\frac{\gamma a}{\alpha}u+cv+\frac{ca}{\alpha}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\gamma vu+\frac{\gamma a}{\alpha}u} Podemos analisar o comportamento em torno do ponto de equilíbrio:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}-\frac{\alpha uv}{\frac{\alpha vc}{\gamma}}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}u=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma vu}{\frac{\gamma au}{\alpha}}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\alpha}{a}v=0} Desprezando os termos não lineares então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} 0 & -\frac{\alpha c}{\gamma}\\ \frac{\gamma a}{\alpha} & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Então os autovalores correspondentes:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\lambda^{2}-\frac{\gamma a}{\alpha}\frac{\alpha c}{\gamma}=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\pm\sqrt{-ac}=\pm\sqrt{ac}i}
Como temos raízes puramente imaginárias e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1}=\lambda_{2}^{*}} , temos um centro, ponto de estabilidade. Isto é, se a condição inicial for próxima de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{a}{\alpha}\right)} o sistema evoluirá de forma que o estado do sistema permanecerá próximo do ponto de equilíbrio.
Segundo método de Lyapunov
Para avaliar o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)} , podemos usar de maneira análoga ao exemplo do segundo critério de Lyapunov:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(\boldsymbol{x}\right)=\frac{x^{2}}{\alpha}-\frac{y^{2}}{\gamma}}
Como já discutimos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}_{0}\right)=0} e a região Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}\left\{ \left(x,y\right)|\left|x\right|>\left|y\right|\right\}} onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)>0} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}\neq\boldsymbol{x}_{0}} , sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}_{0}} um ponto de acumulação em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} [2]. Então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{V}\left(\boldsymbol{x}\right) & =\left[\nabla V\right]\cdot\left[\boldsymbol{f}\left(\boldsymbol{x}\right)\right]\\ & =\left(\frac{2x}{\alpha},-\frac{2y}{\gamma}\right)\left(\dot{x},\dot{y}\right)\\ & =2x^{2}\frac{a}{\alpha}-2x^{2}y+2y^{2}\frac{c}{\gamma}-2y^{2}x\\ & =2x^{2}\left(\frac{a}{\alpha}-y\right)+2y^{2}\left(\frac{c}{\gamma}-x\right)\end{align}} Lembrando do nosso segundo ponto de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{2},y_{2}\right)=\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{V}\left(\boldsymbol{x}\right)=2x^{2}\left(y_{2}-y\right)+2y^{2}\left(x_{2}-x\right)}
Então se estamos próximos suficiente do ponto de equilíbrio em análise Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}
, temos então uma instabilidade local pois Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\left(\boldsymbol{x}\right)>0}
é positivo definido em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}}
, uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|y\right|<\left|y_{2}\right|}
, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|x\right|<\left|x_{2}\right|}
. Olhando o segundo ponto de equilíbrio, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x_{2},y_{2}\right)=\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)}
, podemos manipular as equações da seguinte forma:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dx}{dt}=x\left(a-\alpha y\right)=x\alpha\left(\frac{a}{\alpha}-y\right)=x\alpha\left(y_{2}-y\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dy}{dt}=y\left(-c+\gamma x\right)=y\gamma\left(-\frac{c}{\gamma}+x\right)=y\gamma\left(-x_{2}+x\right)}
Definindo então a seguinte função de Lyapunov:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(x,y\right)=x-x_{2}\left[1+\ln\left(\frac{x}{x_{2}}\right)\right]+\frac{\alpha}{\gamma}\left(y-y_{2}\left[1+\ln\left(\frac{y}{y_{2}}\right)\right]\right)}
Analisando no ponto de e equilíbrio, temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} V\left(x_{2},y_{2}\right) & =x_{2}-x_{2}\left[1+\ln\left(\frac{x_{2}}{x_{2}}\right)\right]+\frac{\alpha}{\gamma}\left(y_{2}-y_{2}\left[1+\ln\left(\frac{y_{2}}{y_{2}}\right)\right]\right)\\ & =x_{2}-x_{2}+\frac{\alpha}{\gamma}\left(y_{2}-y_{2}\right)\\ & =0\end{align}}
Agora precisamos que para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x,y\right)\neq0} tenhamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V>0} , na região próxima ao ponto de equilíbrio. Separando em dois termos:
De forma geral temos , e precisamos que quando . Além de ser facilmente visto via gráfico para todos os valores aceitáveis , também podemos analisar a seguinte desigualdade:
Então:
Solução numérica
Um exemplo resolvido numericamente pode ser visto em Modelo de Lotka-Volterra amortecido, onde foi aproveitado os códigos desenvolvidos para este mesmo.
Versão adimensional
Originalmente temos 4 parâmetros, mas podemos realizar uma série de manipulações visando uma redução da quantidade de parâmetros. Escrevendo o sistema como:
Podemos definir então . Multiplicando ambas equações por :
Se definimos e multiplicamos a segunda equação por :
Agora se multiplicamos a primeira linha e definimos :
Definindo então :
Ou então, ficamos apenas com um único parâmetro.
Separação de variáveis
Aplicando a separação de variáveis, temos então:
Ou ainda, apenas:
Referências
Principais materiais utilizados
- A survey of constructing Lyapunov functions for mathematical models in population biology (Sze-Bi, Revista Taiwanesa de Matemática )
- Estabilidade de pontos de equilíbrio e existência de soluções periódicas em alguns modelos bidimensionais (Salvador Tavares de Oliveira, UNESP)
- Modelagem Matemática e estabilidade de sistemas predador-presa (Paulo Laerte Natti e outros, UEL)
- Modelo de Lotka-Volterra: a dinâmica predador-presa (Rafael Biasi Pata e Elisa Regina Cara, UNIPAMPA)
Citações
- ↑ Análise de sistemas não-lineares (Vilma A. Oliveira e José Ricardo Rosolen, USP)
- ↑ Stability Analysis of Nonlinear Systems (Roberto Zanasi, Universidade de Módena e Reggio Emília)
Anterior: Jogo da Vida | Índice: Ecologia | Próximo: Modelo de Lotka-Volterra amortecido
![{\displaystyle {\begin{aligned}V\left(x,y\right)&=\left[x-x_{2}\left(1+\ln \left({\frac {x}{x_{2}}}\right)\right)\right]+{\frac {\alpha }{\gamma }}\left[y-y_{2}\left(1+\ln \left({\frac {y}{y_{2}}}\right)\right)\right]\\&=V\left(x\right)+{\frac {\alpha }{\gamma }}V\left(y\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/223f3eeff7028162c5517b1c5e13e21bef0bbaba)



![{\textstyle z,z_{2}\in \left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c0364a5cd0d5b9075083435d425526099f185fa)





![{\displaystyle {\begin{aligned}{\dot {V}}\left({\boldsymbol {x}}\right)&=\left[\nabla V\right]\cdot \left[{\boldsymbol {f}}\left({\boldsymbol {x}}\right)\right]\\&=\left[{\frac {\partial V\left(x\right)}{\partial x}},{\frac {\alpha }{\gamma }}{\frac {\partial V\left(y\right)}{\partial y}}\right]\cdot \left[x\alpha \left(y_{2}-y\right),y\gamma \left(-x_{2}+x\right)\right]\\&=\left[1-{\frac {x_{2}}{x}},{\frac {\alpha }{\gamma }}\left(1-{\frac {y_{2}}{y}}\right)\right]\cdot \left[x\alpha \left(y_{2}-y\right),y\gamma \left(-x_{2}+x\right)\right]\\&=\left({\frac {x-x_{2}}{x}}\right)\left(x\alpha \left(y_{2}-y\right)\right)+{\frac {\alpha }{\gamma }}\left({\frac {y-y_{2}}{y}}\right)\left(y\gamma \left(-x_{2}+x\right)\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd0202dbb5817e09f79910d109f57dc7ae700b95)















