Modelo de Lotka-Volterra

Anterior: Modelos Logísticos | Índice: Ecologia | Próximo: Modelo de Lotka-Volterra amortecido

No modelo de Lotka-Volterra temos as seguintes considerações:

• Na ausência de predadores, a população de presas aumenta a uma taxa proporcional à população atual;
• Na ausência de presas, os predadores irão à extinção;
• O número de encontro entre presas e predadores é proporcional a produto das duas populações.
  • Estes encontros beneficiam os predadores em detrimento das presas.

Dessa forma, as equações são:

• ${\textstyle {\frac {dx}{dt}}=x\left(a-\alpha y\right)}$
• ${\textstyle {\frac {dy}{dt}}=y\left(-c+\gamma x\right)}$

Onde:

• ${\textstyle a:}$ taxa de crescimento de presas sem predadores;
• ${\textstyle \alpha :}$taxa de decréscimo da população de presas devido a predação;
• ${\textstyle c:}$ taxa de mortalidade da população de predadores sem presas;
• ${\textstyle \gamma }$: taxa de crescimento de predadores devido a predação.

Separação de variáveis

Utilizando a separação de variáveis, temos:

$${\frac {dy}{dt}}{\frac {dt}{dx}}={\frac {y\left(-c+\gamma x\right)}{x\left(a-\alpha y\right)}}$$

Logo:

$${\frac {dy}{dx}}={\frac {y\left(-c+\gamma x\right)}{x\left(a-\alpha y\right)}}$$

$${\frac {\left(a-\alpha y\right)}{y}}dy={\frac {\left(-c+\gamma x\right)}{x}}dx$$

$$\left({\frac {a}{y}}-\alpha \right)dy=\left(-{\frac {c}{x}}+\gamma \right)dx$$

Integrando ambos os lados:

$$a\ln y-\alpha y=-c\ln x+\gamma x+C$$

$$a\ln y-\alpha y+c\ln x-\gamma x=C$$

Onde ${\textstyle C}$ é uma constante de integração. Para plotarmos um gráfico, considerando apenas ${\textstyle a=\alpha =\gamma =c=1}$ Temos então:

$$\ln y+\ln x-\left(x+y\right)=C$$

Um ponto de equilíbrio fora da origem é obtido quando:

$${\frac {dx}{dt}}=x\left(a-\alpha y\right)=0\rightarrow y={\frac {a}{\alpha }}=1$$

$${\frac {dy}{dt}}=y\left(-c+\gamma x\right)=0\rightarrow x={\frac {c}{\gamma }}=1$$

Então neste caso, o sistema oscila em torno de ${\textstyle \left(1,1\right)}$ e a constante ${\textstyle C}$ é definida pelas condições iniciais ${\textstyle \left(x_{0},y_{0}\right)}$. Para a condição em que ${\textstyle x_{0}=y_{0}=1}$, então:

$$\ln 1+\ln 1-\left(1+1\right)=C$$

$$-2=C$$

Então para este conjunto de parâmetros e condições iniciais:

$$\ln y+\ln x-\left(x+y\right)+2=0$$

Neste caso o sistema vai permanecer no ponto de equilíbrio. Para outras condições iniciais, o sistema vai oscilar em torno do ponto de equilíbrio. Obviamente além do ponto ${\textstyle \left(1,1\right)}$, temos um ponto de equilíbrio em ${\textstyle \left(0,0\right)}$. Vamos analisar a dinâmica na vizinhança dos pontos através de um processo simples de linearização.

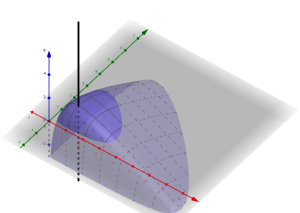
$f\left(x,y\right)=\ln y+\ln x-\left(x+y\right)-C$ com as condições $a=\alpha =c=\gamma =1$ e condição inicial arbitrária, plotado no GeoGebra.

Linearização em torno do ponto de equilíbrio

Primeiro podemos perceber que o sistema é quase-linear em torno de ${\textstyle \left(0,0\right)}$, verificando que satisfaz:

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}\left[{\frac {\text{parte não linear}}{\text{parte linear}}}\right]=0$$

Então lembrando as equações:

• ${\textstyle {\frac {dx}{dt}}=\left[xa\right]-\left(\alpha xy\right)=\left[{\text{linear}}\right]-\left({\text{não linear}}\right)}$
• ${\textstyle {\frac {dy}{dt}}=-\left[yc\right]+\left(\gamma yx\right)=-\left[{\text{linear}}\right]+\left({\text{não linear}}\right)}$

Logo:

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\alpha xy}{xa}}=\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\alpha }{a}}y=0$$

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\gamma xy}{cy}}=\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\gamma }{c}}x=0$$

Desprezando então os termos não lineares podemos escrever o seguinte sistema linearizado em torno da origem:

$$\left({\begin{array}{c}{\dot {x}}\\{\dot {y}}\end{array}}\right)=\left({\begin{array}{cc}a&0\\0&-c\end{array}}\right)\left({\begin{array}{c}x\\y\end{array}}\right)$$

Calculando os autovalores da matriz, obtemos então:

$$-\left(a-\lambda \right)\left(-c-\lambda \right)=0$$

$$\left(a-\lambda \right)\left(c+\lambda \right)=0$$

os seguintes autovalores ${\textstyle \lambda =\left\{a,-c\right\}}$. Como um dos valores tem parte real positiva, então é um ponto instável, especificamente devido aos sinais opostos é um ponto de sela. Como é instável significa que se a condição inicial for próxima de ${\textstyle \left(0,0\right)}$, a evolução do sistema vai se afastar do ponto de equilíbrio. Essa aproximação também indica que próximo do ponto de equilíbrio, a dinâmica pode ser descrita tanto pelo conjunto de equações não lineares, como pelo sistema linear.

Agora o segundo ponto de equilíbrio, de maneira geral é ${\textstyle \left({\frac {c}{\gamma }},{\frac {a}{\alpha }}\right)}$. Primeiro reescrevemos o sistema em torno do ponto de equilíbrio, isto é, fazemos um deslocamento ${\textstyle u=x-{\frac {c}{\gamma }}}$ e ${\textstyle v=y-{\frac {a}{\alpha }}}$. Então temos ${\textstyle dx=du}$ e ${\textstyle dv=dy}$ e substituindo, para ${\textstyle {\dot {x}}}$:

$${\frac {du}{dt}}=\left(u+{\frac {c}{\gamma }}\right)a-\alpha \left(u+{\frac {c}{\gamma }}\right)\left(v+{\frac {a}{\alpha }}\right)$$

$${\frac {du}{dt}}=ua+{\frac {c}{\gamma }}a-\alpha uv-{\frac {\alpha c}{\gamma }}v-ua-{\frac {ca}{\gamma }}$$

$${\frac {du}{dt}}=-\alpha uv-{\frac {\alpha c}{\gamma }}v$$

E para ${\textstyle {\dot {y}}}$:

$${\frac {dv}{dt}}=-\left(v+{\frac {a}{\alpha }}\right)c+\gamma \left(v+{\frac {a}{\alpha }}\right)\left(u+{\frac {c}{\gamma }}\right)$$

$${\frac {dv}{dt}}=-cv-{\frac {ca}{\alpha }}+\gamma vu+{\frac {\gamma a}{\alpha }}u+cv+{\frac {ca}{\alpha }}$$

$${\frac {dv}{dt}}=\gamma vu+{\frac {\gamma a}{\alpha }}u$$

Podemos analisar o comportamento em torno do ponto de equilíbrio:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}-{\frac {\alpha uv}{\frac {\alpha vc}{\gamma }}}=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}-{\frac {\gamma }{c}}u=0$$

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma vu}{\frac {\gamma au}{\alpha }}}=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\alpha }{a}}v=0$$

Desprezando os termos não lineares então:

$$\left({\begin{array}{c}{\dot {u}}\\{\dot {v}}\end{array}}\right)=\left({\begin{array}{cc}0&-{\frac {\alpha c}{\gamma }}\\{\frac {\gamma a}{\alpha }}&0\end{array}}\right)\left({\begin{array}{c}u\\v\end{array}}\right)$$

Então os autovalores correspondentes:

$$-\lambda ^{2}-{\frac {\gamma a}{\alpha }}{\frac {\alpha c}{\gamma }}=0$$

$$\lambda =\pm {\sqrt {-ac}}=\pm {\sqrt {ac}}i$$

Como temos raízes puramente imaginárias e ${\textstyle \lambda _{1}=\lambda _{2}^{*}}$, temos um centro, ponto de estabilidade. Isto é, se a condição inicial for próxima de ${\textstyle \left({\frac {c}{\gamma }},{\frac {a}{\alpha }}\right)}$ o sistema evoluirá de forma que o estado do sistema permanecerá próximo do ponto de equilíbrio.

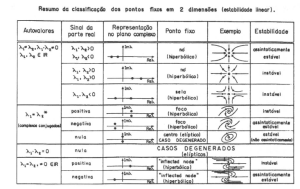
Classificação dos pontos de estabilidade de acordo com os autovalores.

Segundo método de Lyapunov

Para avaliar o ponto ${\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}$, podemos usar de maneira análoga ao exemplo do segundo critério de Lyapunov:

$$V\left({\boldsymbol {x}}\right)={\frac {x^{2}}{\alpha }}-{\frac {y^{2}}{\gamma }}$$

Como já discutimos ${\textstyle V\left({\boldsymbol {x}}_{0}\right)=0}$ e a região ${\textstyle W^{+}\left\{\left(x,y\right)|\left|x\right|>\left|y\right|\right\}}$ onde ${\textstyle V\left({\boldsymbol {x}}\right)>0}$ para ${\textstyle {\boldsymbol {x}}\neq {\boldsymbol {x}}_{0}}$ , sendo ${\textstyle {\boldsymbol {x}}_{0}}$ um ponto de acumulação em ${\textstyle W^{+}}$. Então:

$${\begin{aligned}{\dot {V}}\left({\boldsymbol {x}}\right)&=\left[\nabla V\right]\cdot \left[{\boldsymbol {f}}\left({\boldsymbol {x}}\right)\right]\\&=\left({\frac {2x}{\alpha }},-{\frac {2y}{\gamma }}\right)\left({\dot {x}},{\dot {y}}\right)\\&=2x^{2}{\frac {a}{\alpha }}-2x^{2}y+2y^{2}{\frac {c}{\gamma }}-2y^{2}x\\&=2x^{2}\left({\frac {a}{\alpha }}-y\right)+2y^{2}\left({\frac {c}{\gamma }}-x\right)\end{aligned}}$$

Lembrando do nosso segundo ponto de equilíbrio ${\textstyle \left(x_{2},y_{2}\right)=\left({\frac {c}{\gamma }},{\frac {a}{\alpha }}\right)}$:

$${\dot {V}}\left({\boldsymbol {x}}\right)=2x^{2}\left(y_{2}-y\right)+2y^{2}\left(x_{2}-x\right)$$

Então se estamos próximos suficiente do ponto de equilíbrio em análise ${\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}$, temos então uma instabilidade local pois ${\textstyle {\dot {V}}\left({\boldsymbol {x}}\right)>0}$ é positivo definido em ${\textstyle W^{+}}$, uma vez que ${\textstyle \left|y\right|<\left|y_{2}\right|}$ , ${\textstyle \left|x\right|<\left|x_{2}\right|}$. Olhando o segundo ponto de equilíbrio, ${\textstyle \left(x_{2},y_{2}\right)=\left({\frac {c}{\gamma }},{\frac {a}{\alpha }}\right)}$, podemos manipular as equações da seguinte forma:

• ${\textstyle {\frac {dx}{dt}}=x\left(a-\alpha y\right)=x\alpha \left({\frac {a}{\alpha }}-y\right)=x\alpha \left(y_{2}-y\right)}$
• ${\textstyle {\frac {dy}{dt}}=y\left(-c+\gamma x\right)=y\gamma \left(-{\frac {c}{\gamma }}+x\right)=y\gamma \left(-x_{2}+x\right)}$

Definindo então a seguinte função de Lyapunov:

$$V\left(x,y\right)=x-x_{2}\left[1+\ln \left({\frac {x}{x_{2}}}\right)\right]+{\frac {\alpha }{\gamma }}\left(y-y_{2}\left[1+\ln \left({\frac {y}{y_{2}}}\right)\right]\right)$$

Analisando no ponto de e equilíbrio, temos:

$${\begin{aligned}V\left(x_{2},y_{2}\right)&=x_{2}-x_{2}\left[1+\ln \left({\frac {x_{2}}{x_{2}}}\right)\right]+{\frac {\alpha }{\gamma }}\left(y_{2}-y_{2}\left[1+\ln \left({\frac {y_{2}}{y_{2}}}\right)\right]\right)\\&=x_{2}-x_{2}+{\frac {\alpha }{\gamma }}\left(y_{2}-y_{2}\right)\\&=0\end{aligned}}$$

Agora precisamos que para ${\textstyle \left(x,y\right)\neq 0}$ tenhamos ${\textstyle V>0}$, na região próxima ao ponto de equilíbrio. Separando em dois termos:

$${\begin{aligned}V\left(x,y\right)&=\left[x-x_{2}\left(1+\ln \left({\frac {x}{x_{2}}}\right)\right)\right]+{\frac {\alpha }{\gamma }}\left[y-y_{2}\left(1+\ln \left({\frac {y}{y_{2}}}\right)\right)\right]\\&=V\left(x\right)+{\frac {\alpha }{\gamma }}V\left(y\right)\end{aligned}}$$

De forma geral temos ${\textstyle V\left(z\right)=z-z_{2}\left(1+\ln \left({\frac {z}{z_{2}}}\right)\right)}$, e precisamos que ${\textstyle V\left(z\right)>0}$ quando ${\textstyle z\neq z_{2}}$. Além de ser facilmente visto via gráfico para todos os valores aceitáveis ${\textstyle z,z_{2}\in \left[0,1\right]}$, também podemos analisar a seguinte desigualdade:

$${\begin{aligned}z-z_{2}\left(1+\ln \left({\frac {z}{z_{2}}}\right)\right)&>0\\z&>z_{2}\left(1+\ln \left({\frac {z}{z_{2}}}\right)\right)\\{\frac {z}{z_{2}}}&>1+\ln \left({\frac {z}{z_{2}}}\right)\\e^{\frac {z}{z_{2}}}&>e{\frac {z}{z_{2}}}\\e^{u}&>eu\end{aligned}}$$

Podemos ver quer a desigualdade desigualdade é válida exceto se ${\textstyle x=1}$. Mas como fizemos a seguinte substituição ${\textstyle u={\frac {z}{z_{2}}}}$ então ${\textstyle u=1\rightarrow z=z_{2}}$, e de fato que queremos que seja positiva definida fora do ponto de equilíbrio. Uma vez que sabemos que ${\textstyle V\left(x,y\right)}$ é positivo definido, calculamos então:

$${\begin{aligned}{\dot {V}}\left({\boldsymbol {x}}\right)&=\left[\nabla V\right]\cdot \left[{\boldsymbol {f}}\left({\boldsymbol {x}}\right)\right]\\&=\left[{\frac {\partial V\left(x\right)}{\partial x}},{\frac {\alpha }{\gamma }}{\frac {\partial V\left(y\right)}{\partial y}}\right]\cdot \left[x\alpha \left(y_{2}-y\right),y\gamma \left(-x_{2}+x\right)\right]\\&=\left[1-{\frac {x_{2}}{x}},{\frac {\alpha }{\gamma }}\left(1-{\frac {y_{2}}{y}}\right)\right]\cdot \left[x\alpha \left(y_{2}-y\right),y\gamma \left(-x_{2}+x\right)\right]\\&=\left({\frac {x-x_{2}}{x}}\right)\left(x\alpha \left(y_{2}-y\right)\right)+{\frac {\alpha }{\gamma }}\left({\frac {y-y_{2}}{y}}\right)\left(y\gamma \left(-x_{2}+x\right)\right)\end{aligned}}$$

Então:

$${\dot {V}}\left({\boldsymbol {x}}\right)=\alpha \left(x-x_{2}\right)\left(y_{2}-y\right)-\alpha \left(y_{2}-y\right)\left(x-x_{2}\right)=0$$

Temos então a condição de estabilidade ${\textstyle {\dot {V}}\leq 0}$ concordando como que já havíamos obtidos anteriormente.

Solução numérica

Um exemplo resolvido numericamente pode ser visto em Modelo de Lotka-Volterra amortecido, onde foi aproveitado os códigos desenvolvidos para este mesmo.

Principais materiais utilizados

1. A survey of constructing Lyapunov functions for mathematical models in population biology (Sze-Bi, Revista Taiwanesa de Matemática )
2. Estabilidade de pontos de equilíbrio e existência de soluções periódicas em alguns modelos bidimensionais (Salvador Tavares de Oliveira, UNESP)
3. Modelagem Matemática e estabilidade de sistemas predador-presa (Paulo Laerte Natti e outros, UEL)
4. Modelo de Lotka-Volterra: a dinâmica predador-presa (Rafael Biasi Pata e Elisa Regina Cara, UNIPAMPA)

Citações

Anterior: Modelos Logísticos | Índice: Ecologia | Próximo: Modelo de Lotka-Volterra amortecido