Modelo de Lotka-Volterra amortecido: mudanças entre as edições
(Criou página com '{{Ecologia| [Modelo de Lotka-Volterra amortecido |Modelo de Levins}} {{Ecologia| [Modelo de Lotka-Volterra amortecido |Modelo de Levins}}') |
Sem resumo de edição |
||
| (6 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| | __NOTOC__ | ||
{{Ecologia| | {{Ecologia| [[Modelo de Lotka-Volterra]] |[[Modelo de Levins aprimorado para 2 espécies | Modelo de Levins aprimorado para 2 espécies I]]}} | ||
Uma versão do modelo de Lotka-Volterra aprimorada inclui um termo de saturação na população de presas, isto é, um termo logístico (que inibe o aumento exponencial) visando representar a finitude dos recursos disponíveis para uma espécie. Este modelo é chamado de modelo de Lotka-Volterra amortecido. | |||
* <math display="inline">\frac{dx}{dt}=x\left(a-\alpha y\right)-kx^{2}</math> | |||
* <math display="inline">\frac{dy}{dt}=y\left(-c+\gamma x\right)</math> | |||
Onde <math display="inline">k</math> é uma constante positiva. Agora temos três pontos de equilíbrio, novamente temos <math display="inline">\left(0,0\right)</math>. Mas temos outro ponto quando apenas <math display="inline">y=0</math>: | |||
<math display="block">a-\alpha y-kx=a-kx=0\rightarrow x=\frac{a}{k}</math> | |||
Então <math display="inline">\left(\frac{a}{k},0\right)</math> ou seja um ponto de equilíbrio com apenas a sobrevivência da presa. E ainda temos também um ponto de coexistência entre ambas as espécies: | |||
<math display="block">a-\alpha y-kx=0</math><math display="block">-c+\gamma x=0</math> | |||
Isolando então <math display="inline">x</math> na segunda equação <math display="inline">x=\frac{c}{\gamma}</math> e substituindo na primeira: | |||
<math display="block">a-\alpha y-k\frac{c}{\gamma}=0</math>Então:<math display="block">y=\frac{a}{\alpha}-\frac{kc}{\alpha\gamma}=\frac{\gamma a-kc}{\alpha\gamma}</math> | |||
Então nosso outro ponto de equilíbrio é dado por<math display="inline">\left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)</math>. Infelizmente as equações não são separáveis como no caso anterior, portanto vamos analisar se a equação é semi-linear nas proximidades dos pontos de equilíbrio. Para <math display="inline">\left(0,0\right)</math>: | |||
<math display="block">\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha xy-kx^{2}}{xa}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha y-kx}{a}=0</math><math display="block">\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma xy}{cy}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}x=0</math> | |||
Para <math display="inline">\left(\frac{a}{k},0\right)</math> e fazendo a mudança de variáveis <math display="inline">u=x-\frac{a}{k}</math>, e <math display="inline">v=y</math>, temos: | |||
<math display="block">\frac{du}{dt}=\left(\left(u+\frac{a}{k}\right)a-k\left(u+\frac{a}{k}\right)^{2}\right)-\left(\alpha\left(u+\frac{a}{k}\right)v\right)</math><math display="block">\frac{du}{dt}=\left(ua+\frac{a^{2}}{k}-\left(u^{2}k+\frac{a^{2}}{k}+2ua\right)\right)-\left(\alpha uv+\frac{\alpha a}{k}v\right)</math><math display="block">\frac{du}{dt}=-\left(ua+\frac{\alpha a}{k}v\right)-\left(\alpha uv+u^{2}k\right)</math> | |||
E: | |||
<math display="block">\frac{dv}{dt}=\left(-vc\right)+\left(\gamma v\left(u+\frac{a}{k}\right)\right)=v\left(\gamma\frac{a}{k}-c\right)+\left(\gamma vu\right)</math> | |||
Então: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+u^{2}k}{ua+\frac{\alpha a}{k}v}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+u^{2}k}{u\left(a+\frac{\alpha a}{k}\frac{v}{u}\right)}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha v+uk}{\left(a+\frac{\alpha a}{k}\frac{v}{u}\right)}\right)</math> | |||
Podemos fazer uma substituição de variável novamente usando coordenadas polares<ref>[https://www.math.utah.edu/lectures/math2210/12PostNotes.pdf Limits and Continuity] (Rebecca Noonan-Heale ,Universidade de Utah)</ref> <math display="inline">r^{2}=u^{2}+v^{2}</math> e <math display="inline">u=r\cos\theta</math>, <math display="inline">v=r\sin\theta</math>, então: | |||
<math display="block">\lim_{r\rightarrow0}\left(\frac{\alpha r\sin\theta+kr\cos\theta}{\left(a+\frac{\alpha a}{k}\frac{r\sin\theta}{r\cos\theta}\right)}\right)=\lim_{r\rightarrow0}\left(\frac{\alpha kr\sin\theta+k^{2}r\cos\theta}{\left(ka+\alpha a\tan\theta\right)}\right)=0</math> | |||
E o limite: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma vu}{v\left(\gamma\frac{a}{k}-c\right)}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma u}{\left(\gamma\frac{a}{k}-c\right)}=0</math> | |||
E por fim, vamos estudar os pontos de estabilidade em torno de <math display="inline">\left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)</math>, tendo agora <math display="inline">u=x-\frac{c}{\gamma}</math> e <math display="inline">v=\frac{\gamma a-kc}{\alpha\gamma}-y</math>, então, manipulando novamente, primeiro trabalhando com <math>\dot{x}</math>: | |||
<math display="block">\frac{dx}{dt}=\left(xa-kx^{2}\right)-\left(\alpha xy\right)</math><math display="block">\frac{du}{dt}=\left(\left(\frac{c}{\gamma}+u\right)a-k\left(\frac{c}{\gamma}+u\right)^{2}\right)-\left(\alpha\left(\frac{c}{\gamma}+u\right)\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)\right)</math><math display="block">\frac{du}{dt}=\left(\frac{ca}{\gamma}+au-\frac{kc^{2}}{\gamma^{2}}-ku^{2}-\frac{2ck}{\gamma}u\right)-\left(\frac{c\alpha}{\gamma}v+\frac{\gamma ac-kc^{2}}{\gamma^{2}}+\alpha uv+\left[\frac{\gamma a-kc}{\gamma}\right]u\right)</math><math display="block">\frac{du}{dt}=\left(\left(\frac{ca}{\gamma}-\frac{kc^{2}}{\gamma^{2}}-\frac{\gamma ac-kc^{2}}{\gamma^{2}}\right)+\left(a-\frac{2ck}{\gamma}-\left[\frac{\gamma a-kc}{\gamma}\right]-ku\right)u-\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv\right)</math><math display="block">\frac{du}{dt}=\left(\left(-\frac{kc}{\gamma}-ku\right)u-\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv\right)</math><math display="block">\frac{du}{dt}=-\left(\frac{kc}{\gamma}u+\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv+ku^{2}\right)</math> | |||
E com <math>\dot{y}</math>: | |||
<math display="block">\frac{dy}{dt}=\left(-yc\right)+\left(\gamma yx\right)</math><math display="block">\frac{dv}{dt}=\left(-\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)c\right)+\left(\gamma\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)\left(\frac{c}{\gamma}+u\right)\right)</math><math display="block">\frac{dv}{dt}=\left(-vc-\frac{ac}{\alpha}+\frac{kc^{2}}{\alpha\gamma}\right)+\left(vc+\frac{\gamma ac-kc^{2}}{\alpha\gamma}+\gamma uv+\left[\frac{\gamma a-kc}{\alpha}\right]u\right)</math><math display="block">\frac{dv}{dt}=\gamma uv+\left[\frac{\gamma a-kc}{\alpha}\right]u</math> | |||
Calculando então os limites, relacionado a <math>u</math>: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+ku^{2}}{\frac{kc}{\gamma}u+\frac{c\alpha}{\gamma}v}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+ku^{2}}{u\left(\frac{kc}{\gamma}+\frac{c\alpha}{\gamma}\frac{v}{u}\right)}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha v+ku}{\frac{kc}{\gamma}+\frac{c\alpha}{\gamma}\frac{v}{u}}\right)</math> | |||
E novamente fazendo a substituição <math display="inline">r^{2}=u^{2}+v^{2}</math> e <math display="inline">u=r\cos\theta</math>, <math display="inline">v=r\sin\theta</math>, então: | |||
<math display="block">\lim_{r\rightarrow0}\left(\frac{\alpha r\sin\theta+kr\cos\theta}{\frac{kc}{\gamma}+\frac{c\alpha}{\gamma}\frac{r\sin\theta}{r\cos\theta}}\right)=\lim_{r\rightarrow0}\left(\frac{r\alpha\gamma\sin\theta+rk\gamma\cos\theta}{kc+c\alpha\tan\theta}\right)=0</math> | |||
E a <math>v</math>: | |||
<math display="block">\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma uv}{\left[\frac{\gamma a-kc}{\alpha}\right]u}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma v}{\left[\frac{\gamma a-kc}{\alpha}\right]}=0</math> | |||
Então os três pontos são semi-lineares. A partir disto, podemos analisar os tipos de estabilidades. Para <math display="inline">\left(0,0\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
a & 0\\ | |||
0 & -c | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)</math> | |||
Então: | |||
<math display="block">\left(a-\lambda\right)\left(c+\lambda\right)=0</math> Novamente temos duas raízes reais de sinais opostos, então temos um ponto de sela, uma instabilidade. Para o segundo ponto: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-a & -\frac{\alpha a}{k}\\ | |||
0 & \gamma\frac{a}{k}-c | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math> | |||
Então: | |||
<math display="block">\left(-a-\lambda\right)\left(\left(\frac{\gamma a}{k}-c\right)-\lambda\right)=0</math><math display="block">\left(a+\lambda\right)\left(\left(\frac{\gamma a}{k}-c\right)-\lambda\right)=0</math> | |||
Temos duas raízes reais uma é negativa <math display="inline">\lambda_{1}=-a</math>. Porém a classificação do ponto depende dos parâmetros escolhidos. Se <math display="inline">\left(\frac{\gamma a}{k}-c\right)>0</math> ou seja <math display="inline">\gamma a>ck</math>, temos uma instabilidade, uma sela, mas se <math display="inline">\gamma a<ck</math>, então temos um nó hiperbólico, ou seja, estabilidade. E por último: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-\frac{kc}{\gamma} & -\frac{c\alpha}{\gamma}\\ | |||
\frac{\gamma a-kc}{\alpha} & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math> | |||
Então: | |||
<math display="block">\left(\frac{kc}{\gamma}+\lambda\right)\lambda+\frac{c\alpha}{\gamma}\left(\frac{\gamma a-kc}{\alpha}\right)=0</math><math display="block">\gamma\lambda^{2}+kc\lambda+c\left(\gamma a-kc\right)=0</math> | |||
Então: | |||
<math display="block">\lambda=-\left(\frac{kc}{2\gamma}\right)\pm\frac{\sqrt{\left(kc\right)^{2}-4\gamma c\left(\gamma a-kc\right)}}{2\gamma}</math><math display="block">\lambda=-\left(\frac{kc}{2\gamma}\right)\pm\frac{\sqrt{\left[\left(kc\right)^{2}+4\gamma c^{2}k\right]-4c\gamma^{2}a}}{2\gamma}</math> | |||
Então o comportamento do sistema vai depender da escolha de parâmetros, porém como todas constantes são positivas <math display="inline">-\left(\frac{kc}{2\gamma}\right)</math> vai ser sempre negativo, e a única forma de ser instável é se <math display="inline">\left(kc\right)^{2}+4\gamma c^{2}k>4c\gamma^{2}a</math>, para garantir que o número seja real, e ainda <math display="inline">\frac{\sqrt{\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a}}{2\gamma}>\frac{kc}{2\gamma}</math> para que o autovalor seja positivo. Analisando então essa última desigualdade: | |||
<math display="block">\frac{\sqrt{\left(kc\right)^{2}+4\gamma c^{2}kc-4c\gamma^{2}a}}{2\gamma}>\frac{kc}{2\gamma}</math><math display="block">\sqrt{\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a}>kc</math> | |||
Elevando ao quadrado: | |||
<math display="block">\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a>\left(kc\right)^{2}</math><math display="block">4\gamma c^{2}k-4c\gamma^{2}a>0</math> | |||
Dividindo por <math display="inline">4c\gamma</math> | |||
<math display="block">ck-\gamma a>0</math><math display="block">ck>\gamma a</math> | |||
Então essa é a condição para que o autovalor seja positivo. E olhando pra primeira desigualdade: | |||
<math display="block">\left(kc\right)^{2}+4\gamma c^{2}k>4c\gamma^{2}a</math><math display="block">\frac{k^{2}c}{4\gamma}+ck>\gamma a</math> | |||
Para garantir que o número seja real. Então temos duas desigualdades para satisfazer para que seja instável: | |||
* <math display="inline">ck>\gamma a</math> | |||
* <math display="inline">\frac{k^{2}c}{4\gamma}+ck>\gamma a</math> | |||
Como <math display="inline">\left(\frac{k^{2}c}{4\gamma}\right)</math> é necessariamente um termo positivo: | |||
<math display="block">\gamma a<ck<\frac{k^{2}c}{4\gamma}+ck</math> | |||
Ou seja, podemos restringir a condição de instabilidade para <math display="inline">ck>\gamma a</math> pois <math display="inline">ck<\frac{k^{2}c}{4\gamma}+ck</math> é uma desigualdade válida para qualquer escolha de parâmetros válidos. Mas lembrando que para o outro ponto é estável se <math display="inline">ck>\gamma a</math> , então sempre temos um ponto de equilíbrio estável e outro instável (além do a instabilidade na origem). Ou seja, por exemplo para valores mais baixos de de <math display="inline">c</math> (termo de crescimento dos predadores) ou <math display="inline">k</math> (termo de amortecimento da presa) temos coexistência de ambas as espécies, se aumentar estes parâmetros, somente a presa sobrevive. Além disso, quando temos <math display="inline">k=0</math>: | |||
<math display="block">\lambda=\pm\frac{\sqrt{-4c\gamma^{2}a}}{2\gamma}=\pm i\sqrt{ca}</math> | |||
Ou seja, temos apenas a parte imaginária, e retornamos à estabilidade do centro. Dessa forma <math display="inline">k=0</math> ou <math display="inline">k\neq0</math> determina se o sistema atinge equilíbrio ou permanece oscilatório, e depois o conjunto de parâmetros, caso atinja estabilidade, determina se ela é atingida com ou sem predadores. | |||
== Exemplo == | |||
Para estudarmos melhor uma situação, vamos escolher os parâmetros: <math display="inline">a=1</math>, <math display="inline">\alpha=0.5</math>, <math display="inline">k=0.5</math>, <math display="inline">c=0.75</math>,<math display="inline">\gamma=0.5</math>. Então os pontos de equilíbrio são: | |||
*<math display="inline">\left(0,0\right)\rightarrow\lambda=\left\{ 1,-0.75\right\}</math>, uma sela, instável; | |||
*<math display="inline">\left(2,0\right)\rightarrow\lambda=\left\{ -1,0.25\right\}</math>, outro ponto instável, outra sela; | |||
*<math display="inline">\left(1.5,0.5\right)\rightarrow\lambda=\left\{ -0.375+0.22i,-0.375-0.22i\right\}</math>, agora temos um nó assintoticamente estável, pois as parte reais são negativas e as imaginárias são os conjugados. | |||
E fazendo um rascunho do plano de fases, próximo de <math display="inline">\left(0,0\right)</math>, desprezando então os termos não-lineares: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
a & 0\\ | |||
0 & -c | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
1 & 0\\ | |||
0 & -0.75 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{c} | |||
x\\ | |||
-0.75y | |||
\end{array}\right)</math> | |||
Próximo a <math display="inline">\left(\frac{a}{k},0\right)=\left(2,0\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-a & -\frac{\alpha a}{k}\\ | |||
& \gamma\frac{a}{k}-c | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-1 & -1\\ | |||
& 0.25 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-1 & -1\\ | |||
& 0.25 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x-2\\ | |||
y | |||
\end{array}\right)=\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{c} | |||
\left(2-x\right)-y\\ | |||
0.25y | |||
\end{array}\right)</math> | |||
De <math display="inline">\left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)=\left(1.5,0.5\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-\frac{kc}{\gamma} & -\frac{c\alpha}{\gamma}\\ | |||
\frac{\gamma a-kc}{\alpha} & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-0.75 & -0.75\\ | |||
0.25 & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
-0.75 & -0.75\\ | |||
0.25 & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x-1.5\\ | |||
y-0.5 | |||
\end{array}\right)=\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{c} | |||
0.75\left[\left(1.5-x\right)+\left(0.5-y\right)\right]\\ | |||
0.25\left(x-1.5\right) | |||
\end{array}\right)</math> | |||
Plotando temos então: | |||
[[Ficheiro:LVA.png|centro|miniaturadaimagem|A esquerda o rascunho do diagrama de fases, e a direita a evolução do sistema para as condições iniciais <math display="inline">\left(x_{0},y_{0}\right)=\left(2,0.05\right)</math>.|741x262px]] | |||
Por curiosidade, se fazemos <math display="inline">k=0</math>: Para <math display="inline">\left(0,0\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
a & 0\\ | |||
0 & -c | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
1 & 0\\ | |||
0 & -0.75 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x\\ | |||
y | |||
\end{array}\right)</math> | |||
E para <math display="inline">\left(\frac{c}{\gamma},\frac{a}{\alpha}\right)=\left(1.5,2.0\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{u}\\ | |||
\dot{v} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
0 & -\frac{\alpha c}{\gamma}\\ | |||
\frac{\gamma a}{\alpha} & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
u\\ | |||
v | |||
\end{array}\right)</math><math display="block">\left(\begin{array}{c} | |||
\dot{x}\\ | |||
\dot{y} | |||
\end{array}\right)=\left(\begin{array}{cc} | |||
0 & -0.75\\ | |||
1 & 0 | |||
\end{array}\right)\left(\begin{array}{c} | |||
x-1.5\\ | |||
y-2 | |||
\end{array}\right)=\left(\begin{array}{c} | |||
-0.75(y-2)\\ | |||
x-1.5 | |||
\end{array}\right)</math>Plotando o resultado: | |||
[[Ficheiro:LV.png|centro|miniaturadaimagem|A direita o rascunho do diagrama de fase, e a esquerda a evolução para as condições iniciais <math display="inline">\left(x_{0},y_{0}\right)=\left(1,0.5\right)</math>.|741x262px]] | |||
====== Códigos ====== | |||
Os seguintes códigos escritos em Python foram utilizados para obter a solução numérica e plotar o rascunho do diagrama de fases próximo aos pontos de equilíbrio. | |||
<pre> | |||
import matplotlib.pyplot as plt | |||
import numpy as np | |||
# LOTKA-VOLTERRA: Solução numérica | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
def sol_lot(): | |||
x=[] | |||
y=[] | |||
x.append(1) # População inicial de presas | |||
y.append(0.5) # População inicial de predadores | |||
N=400000 # Quantidade de passos | |||
d=0.0001 # Tamanhodos passos | |||
a=0 # 1: Amortecido, 0: Sem amortecimento | |||
for i in range(N-1): | |||
x.append(x[i]+d*(x[i]*(1-0.5*y[i])-0.5*x[i]*x[i]*a)) | |||
y.append(y[i]+d*(y[i]*(-0.75+0.5*x[i]))) | |||
#Plotamos a evolução temporal das frações de população | |||
X=np.arange(len(x)) #Eixo x | |||
plt.plot(X,x,'b-') | |||
plt.plot(X,y,'k-') | |||
plt.xlabel('Passo') | |||
plt.ylim(0,6) | |||
plt.show() | |||
</pre> | |||
A função abaixo tem como finalidade plotar um rascunho do plano de fase próximo ao pontos de equilíbrio do sistema: | |||
<pre> | |||
import matplotlib.pyplot as plt | |||
import numpy as np | |||
# LOTKA-VOLTERRA: Plano de fase | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
def phase_lot(): | |||
X = np.arange(0, 4, 0.2) # Eixo x | |||
Y = np.arange(0, 4, 0.2) # Eixo Y | |||
U,V=np.meshgrid(X,Y) | |||
p1=[0.,0.] # Ponto de equilíbrio 1 | |||
p2=[1.5,2.0] # Ponto de equilíbrio 2 | |||
p3=[1.5*100,0.5*100] # Ponto de equilíbrio 3 | |||
c=0 | |||
for x in X: | |||
l=0 | |||
for y in Y: | |||
#Distâncias | |||
d1=np.sqrt((x-p1[0])*(x-p1[0])+(y-p1[1])*(y-p1[1])) | |||
d2=np.sqrt((x-p2[0])*(x-p2[0])+(y-p2[1])*(y-p2[1])) | |||
d3=np.sqrt((x-p3[0])*(x-p3[0])+(y-p3[1])*(y-p3[1])) | |||
#encontrar o ponto de equilíbrio mais próximo | |||
p=1 | |||
if(d2<d1): | |||
p=2 | |||
if(d3<d2): | |||
p=3 | |||
elif(d3<d1): | |||
p=3 | |||
# Calculamos o vetor de variação do estado baseado no ponto mais próximo: | |||
# [dx/dt,dy/dt]=[a,b] | |||
if(p==1): | |||
a=x | |||
b=-0.75*y | |||
elif(p==2): | |||
a=-0.75*(y-2) | |||
b=x-1.5 | |||
elif(p==3): | |||
a=0.75*((1.5-x)+(0.5-y)) | |||
b=0.25*(x-1.5) | |||
else: | |||
print("Algo deu errado") | |||
m=np.sqrt(a*a+b*b) # Módulo do vetor para normalizar | |||
if(m==0): | |||
m=1 | |||
U[l,c]=a/m | |||
V[l,c]=b/m | |||
l=l+1 | |||
c=c+1 | |||
# Plotamos o resultado | |||
fig, ax = plt.subplots() | |||
ax.quiver(X, Y, U, V) # Os vetores | |||
plt.plot(p1[0],p1[1],'ro') # O ponto de equilíbrio 1 | |||
plt.plot(p2[0],p2[1],'go') # O ponto de equilíbrio 2 | |||
plt.plot(p3[0],p3[1],'go') # O ponto de equilíbrio 3 | |||
plt.show() | |||
</pre> | |||
====== Principais materiais utilizados ====== | |||
# [https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-i-first-order-differential-equations/numerical-methods/ Numerical Methods] (Instituto de Tecnologia de Massachusetts) | |||
# [https://web.mit.edu/10.001/Web/Course_Notes/Differential_Equations_Notes/lec24.html Numerical Solution of Ordinary Differential Equations] (R. Sureshkumar,Instituto de Tecnologia de Massachusetts) | |||
# A estes materiais, somam-se os vistos em [[Modelo de Lotka-Volterra]] | |||
====== Citações ====== | |||
<references /> | |||
{{Ecologia| [[Modelo de Lotka-Volterra]] |[[Modelo de Levins aprimorado para 2 espécies | Modelo de Levins aprimorado para 2 espécies I]]}} | |||
Edição atual tal como às 17h44min de 2 de maio de 2021
Anterior: Modelo de Lotka-Volterra | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies I
Uma versão do modelo de Lotka-Volterra aprimorada inclui um termo de saturação na população de presas, isto é, um termo logístico (que inibe o aumento exponencial) visando representar a finitude dos recursos disponíveis para uma espécie. Este modelo é chamado de modelo de Lotka-Volterra amortecido.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dx}{dt}=x\left(a-\alpha y\right)-kx^{2}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{dy}{dt}=y\left(-c+\gamma x\right)}
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k} é uma constante positiva. Agora temos três pontos de equilíbrio, novamente temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} . Mas temos outro ponto quando apenas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle y=0} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a-\alpha y-kx=a-kx=0\rightarrow x=\frac{a}{k}}
Então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{a}{k},0\right)} ou seja um ponto de equilíbrio com apenas a sobrevivência da presa. E ainda temos também um ponto de coexistência entre ambas as espécies:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a-\alpha y-kx=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -c+\gamma x=0}
Isolando então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x} na segunda equação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x=\frac{c}{\gamma}} e substituindo na primeira:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a-\alpha y-k\frac{c}{\gamma}=0} Então:Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\frac{a}{\alpha}-\frac{kc}{\alpha\gamma}=\frac{\gamma a-kc}{\alpha\gamma}}
Então nosso outro ponto de equilíbrio é dado porFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)} . Infelizmente as equações não são separáveis como no caso anterior, portanto vamos analisar se a equação é semi-linear nas proximidades dos pontos de equilíbrio. Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha xy-kx^{2}}{xa}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\alpha y-kx}{a}=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma xy}{cy}=\lim_{\left(x,y\right)\rightarrow\left(0,0\right)}-\frac{\gamma}{c}x=0}
Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{a}{k},0\right)} e fazendo a mudança de variáveis Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=x-\frac{a}{k}} , e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v=y} , temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left(\left(u+\frac{a}{k}\right)a-k\left(u+\frac{a}{k}\right)^{2}\right)-\left(\alpha\left(u+\frac{a}{k}\right)v\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left(ua+\frac{a^{2}}{k}-\left(u^{2}k+\frac{a^{2}}{k}+2ua\right)\right)-\left(\alpha uv+\frac{\alpha a}{k}v\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=-\left(ua+\frac{\alpha a}{k}v\right)-\left(\alpha uv+u^{2}k\right)}
E:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\left(-vc\right)+\left(\gamma v\left(u+\frac{a}{k}\right)\right)=v\left(\gamma\frac{a}{k}-c\right)+\left(\gamma vu\right)}
Então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+u^{2}k}{ua+\frac{\alpha a}{k}v}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+u^{2}k}{u\left(a+\frac{\alpha a}{k}\frac{v}{u}\right)}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha v+uk}{\left(a+\frac{\alpha a}{k}\frac{v}{u}\right)}\right)}
Podemos fazer uma substituição de variável novamente usando coordenadas polares[1] Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r^{2}=u^{2}+v^{2}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=r\cos\theta} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v=r\sin\theta} , então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r\rightarrow0}\left(\frac{\alpha r\sin\theta+kr\cos\theta}{\left(a+\frac{\alpha a}{k}\frac{r\sin\theta}{r\cos\theta}\right)}\right)=\lim_{r\rightarrow0}\left(\frac{\alpha kr\sin\theta+k^{2}r\cos\theta}{\left(ka+\alpha a\tan\theta\right)}\right)=0}
E o limite:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma vu}{v\left(\gamma\frac{a}{k}-c\right)}=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\frac{\gamma u}{\left(\gamma\frac{a}{k}-c\right)}=0}
E por fim, vamos estudar os pontos de estabilidade em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)} , tendo agora Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=x-\frac{c}{\gamma}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v=\frac{\gamma a-kc}{\alpha\gamma}-y} , então, manipulando novamente, primeiro trabalhando com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{x}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=\left(xa-kx^{2}\right)-\left(\alpha xy\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left(\left(\frac{c}{\gamma}+u\right)a-k\left(\frac{c}{\gamma}+u\right)^{2}\right)-\left(\alpha\left(\frac{c}{\gamma}+u\right)\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left(\frac{ca}{\gamma}+au-\frac{kc^{2}}{\gamma^{2}}-ku^{2}-\frac{2ck}{\gamma}u\right)-\left(\frac{c\alpha}{\gamma}v+\frac{\gamma ac-kc^{2}}{\gamma^{2}}+\alpha uv+\left[\frac{\gamma a-kc}{\gamma}\right]u\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left(\left(\frac{ca}{\gamma}-\frac{kc^{2}}{\gamma^{2}}-\frac{\gamma ac-kc^{2}}{\gamma^{2}}\right)+\left(a-\frac{2ck}{\gamma}-\left[\frac{\gamma a-kc}{\gamma}\right]-ku\right)u-\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=\left(\left(-\frac{kc}{\gamma}-ku\right)u-\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=-\left(\frac{kc}{\gamma}u+\frac{c\alpha}{\gamma}v\right)-\left(\alpha uv+ku^{2}\right)}
E com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{y}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}=\left(-yc\right)+\left(\gamma yx\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\left(-\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)c\right)+\left(\gamma\left(v+\frac{\gamma a-kc}{\alpha\gamma}\right)\left(\frac{c}{\gamma}+u\right)\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\left(-vc-\frac{ac}{\alpha}+\frac{kc^{2}}{\alpha\gamma}\right)+\left(vc+\frac{\gamma ac-kc^{2}}{\alpha\gamma}+\gamma uv+\left[\frac{\gamma a-kc}{\alpha}\right]u\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}=\gamma uv+\left[\frac{\gamma a-kc}{\alpha}\right]u}
Calculando então os limites, relacionado a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+ku^{2}}{\frac{kc}{\gamma}u+\frac{c\alpha}{\gamma}v}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha uv+ku^{2}}{u\left(\frac{kc}{\gamma}+\frac{c\alpha}{\gamma}\frac{v}{u}\right)}\right)=\lim_{\left(u,v\right)\rightarrow\left(0,0\right)}\left(\frac{\alpha v+ku}{\frac{kc}{\gamma}+\frac{c\alpha}{\gamma}\frac{v}{u}}\right)}
E novamente fazendo a substituição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r^{2}=u^{2}+v^{2}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u=r\cos\theta} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v=r\sin\theta} , então:
E a :
Então os três pontos são semi-lineares. A partir disto, podemos analisar os tipos de estabilidades. Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} a & 0\\ 0 & -c \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)}
Então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(a-\lambda\right)\left(c+\lambda\right)=0} Novamente temos duas raízes reais de sinais opostos, então temos um ponto de sela, uma instabilidade. Para o segundo ponto:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -a & -\frac{\alpha a}{k}\\ 0 & \gamma\frac{a}{k}-c \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)}
Então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-a-\lambda\right)\left(\left(\frac{\gamma a}{k}-c\right)-\lambda\right)=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(a+\lambda\right)\left(\left(\frac{\gamma a}{k}-c\right)-\lambda\right)=0}
Temos duas raízes reais uma é negativa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1}=-a} . Porém a classificação do ponto depende dos parâmetros escolhidos. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{\gamma a}{k}-c\right)>0} ou seja Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \gamma a>ck} , temos uma instabilidade, uma sela, mas se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \gamma a<ck} , então temos um nó hiperbólico, ou seja, estabilidade. E por último:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -\frac{kc}{\gamma} & -\frac{c\alpha}{\gamma}\\ \frac{\gamma a-kc}{\alpha} & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)}
Então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{kc}{\gamma}+\lambda\right)\lambda+\frac{c\alpha}{\gamma}\left(\frac{\gamma a-kc}{\alpha}\right)=0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma\lambda^{2}+kc\lambda+c\left(\gamma a-kc\right)=0}
Então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=-\left(\frac{kc}{2\gamma}\right)\pm\frac{\sqrt{\left(kc\right)^{2}-4\gamma c\left(\gamma a-kc\right)}}{2\gamma}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=-\left(\frac{kc}{2\gamma}\right)\pm\frac{\sqrt{\left[\left(kc\right)^{2}+4\gamma c^{2}k\right]-4c\gamma^{2}a}}{2\gamma}}
Então o comportamento do sistema vai depender da escolha de parâmetros, porém como todas constantes são positivas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle -\left(\frac{kc}{2\gamma}\right)} vai ser sempre negativo, e a única forma de ser instável é se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(kc\right)^{2}+4\gamma c^{2}k>4c\gamma^{2}a} , para garantir que o número seja real, e ainda Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{\sqrt{\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a}}{2\gamma}>\frac{kc}{2\gamma}} para que o autovalor seja positivo. Analisando então essa última desigualdade:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sqrt{\left(kc\right)^{2}+4\gamma c^{2}kc-4c\gamma^{2}a}}{2\gamma}>\frac{kc}{2\gamma}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a}>kc}
Elevando ao quadrado:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(kc\right)^{2}+4\gamma c^{2}k-4c\gamma^{2}a>\left(kc\right)^{2}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4\gamma c^{2}k-4c\gamma^{2}a>0}
Dividindo por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 4c\gamma}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ck-\gamma a>0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ck>\gamma a}
Então essa é a condição para que o autovalor seja positivo. E olhando pra primeira desigualdade:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(kc\right)^{2}+4\gamma c^{2}k>4c\gamma^{2}a} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{k^{2}c}{4\gamma}+ck>\gamma a}
Para garantir que o número seja real. Então temos duas desigualdades para satisfazer para que seja instável:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ck>\gamma a}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac{k^{2}c}{4\gamma}+ck>\gamma a}
Como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{k^{2}c}{4\gamma}\right)} é necessariamente um termo positivo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma a<ck<\frac{k^{2}c}{4\gamma}+ck}
Ou seja, podemos restringir a condição de instabilidade para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ck>\gamma a} pois Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ck<\frac{k^{2}c}{4\gamma}+ck} é uma desigualdade válida para qualquer escolha de parâmetros válidos. Mas lembrando que para o outro ponto é estável se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ck>\gamma a} , então sempre temos um ponto de equilíbrio estável e outro instável (além do a instabilidade na origem). Ou seja, por exemplo para valores mais baixos de de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c} (termo de crescimento dos predadores) ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k} (termo de amortecimento da presa) temos coexistência de ambas as espécies, se aumentar estes parâmetros, somente a presa sobrevive. Além disso, quando temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=0} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\pm\frac{\sqrt{-4c\gamma^{2}a}}{2\gamma}=\pm i\sqrt{ca}}
Ou seja, temos apenas a parte imaginária, e retornamos à estabilidade do centro. Dessa forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=0} ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k\neq0} determina se o sistema atinge equilíbrio ou permanece oscilatório, e depois o conjunto de parâmetros, caso atinja estabilidade, determina se ela é atingida com ou sem predadores.
Exemplo
Para estudarmos melhor uma situação, vamos escolher os parâmetros: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle a=1} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha=0.5} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=0.5} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c=0.75} ,Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \gamma=0.5} . Então os pontos de equilíbrio são:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)\rightarrow\lambda=\left\{ 1,-0.75\right\}} , uma sela, instável;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(2,0\right)\rightarrow\lambda=\left\{ -1,0.25\right\}} , outro ponto instável, outra sela;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(1.5,0.5\right)\rightarrow\lambda=\left\{ -0.375+0.22i,-0.375-0.22i\right\}} , agora temos um nó assintoticamente estável, pois as parte reais são negativas e as imaginárias são os conjugados.
E fazendo um rascunho do plano de fases, próximo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)} , desprezando então os termos não-lineares:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} a & 0\\ 0 & -c \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & -0.75 \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{c} x\\ -0.75y \end{array}\right)}
Próximo a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{a}{k},0\right)=\left(2,0\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -a & -\frac{\alpha a}{k}\\ & \gamma\frac{a}{k}-c \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -1 & -1\\ & 0.25 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)=\left(\begin{array}{cc} -1 & -1\\ & 0.25 \end{array}\right)\left(\begin{array}{c} x-2\\ y \end{array}\right)=\left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{c} \left(2-x\right)-y\\ 0.25y \end{array}\right)}
De Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{\gamma a-kc}{\alpha\gamma}\right)=\left(1.5,0.5\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -\frac{kc}{\gamma} & -\frac{c\alpha}{\gamma}\\ \frac{\gamma a-kc}{\alpha} & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} -0.75 & -0.75\\ 0.25 & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)=\left(\begin{array}{cc} -0.75 & -0.75\\ 0.25 & 0 \end{array}\right)\left(\begin{array}{c} x-1.5\\ y-0.5 \end{array}\right)=\left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{c} 0.75\left[\left(1.5-x\right)+\left(0.5-y\right)\right]\\ 0.25\left(x-1.5\right) \end{array}\right)}
Plotando temos então:
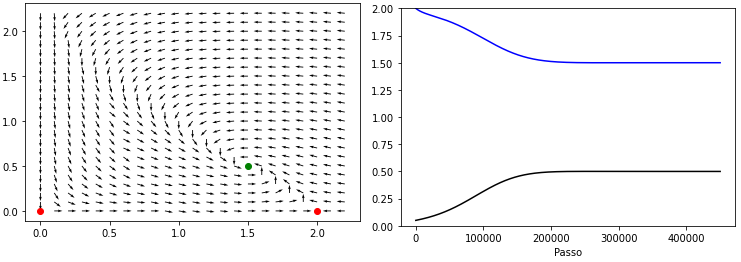
Por curiosidade, se fazemos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=0}
: Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(0,0\right)}
:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} a & 0\\ 0 & -c \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & -0.75 \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)}
E para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\frac{c}{\gamma},\frac{a}{\alpha}\right)=\left(1.5,2.0\right)} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right)=\left(\begin{array}{cc} 0 & -\frac{\alpha c}{\gamma}\\ \frac{\gamma a}{\alpha} & 0 \end{array}\right)\left(\begin{array}{c} u\\ v \end{array}\right)} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} 0 & -0.75\\ 1 & 0 \end{array}\right)\left(\begin{array}{c} x-1.5\\ y-2 \end{array}\right)=\left(\begin{array}{c} -0.75(y-2)\\ x-1.5 \end{array}\right)} Plotando o resultado:
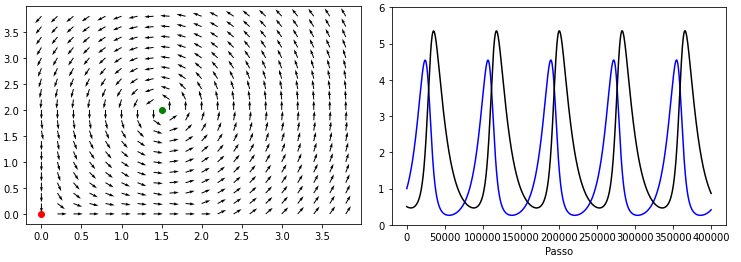
Códigos
Os seguintes códigos escritos em Python foram utilizados para obter a solução numérica e plotar o rascunho do diagrama de fases próximo aos pontos de equilíbrio.
import matplotlib.pyplot as plt
import numpy as np
# LOTKA-VOLTERRA: Solução numérica
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
def sol_lot():
x=[]
y=[]
x.append(1) # População inicial de presas
y.append(0.5) # População inicial de predadores
N=400000 # Quantidade de passos
d=0.0001 # Tamanhodos passos
a=0 # 1: Amortecido, 0: Sem amortecimento
for i in range(N-1):
x.append(x[i]+d*(x[i]*(1-0.5*y[i])-0.5*x[i]*x[i]*a))
y.append(y[i]+d*(y[i]*(-0.75+0.5*x[i])))
#Plotamos a evolução temporal das frações de população
X=np.arange(len(x)) #Eixo x
plt.plot(X,x,'b-')
plt.plot(X,y,'k-')
plt.xlabel('Passo')
plt.ylim(0,6)
plt.show()
A função abaixo tem como finalidade plotar um rascunho do plano de fase próximo ao pontos de equilíbrio do sistema:
import matplotlib.pyplot as plt
import numpy as np
# LOTKA-VOLTERRA: Plano de fase
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
def phase_lot():
X = np.arange(0, 4, 0.2) # Eixo x
Y = np.arange(0, 4, 0.2) # Eixo Y
U,V=np.meshgrid(X,Y)
p1=[0.,0.] # Ponto de equilíbrio 1
p2=[1.5,2.0] # Ponto de equilíbrio 2
p3=[1.5*100,0.5*100] # Ponto de equilíbrio 3
c=0
for x in X:
l=0
for y in Y:
#Distâncias
d1=np.sqrt((x-p1[0])*(x-p1[0])+(y-p1[1])*(y-p1[1]))
d2=np.sqrt((x-p2[0])*(x-p2[0])+(y-p2[1])*(y-p2[1]))
d3=np.sqrt((x-p3[0])*(x-p3[0])+(y-p3[1])*(y-p3[1]))
#encontrar o ponto de equilíbrio mais próximo
p=1
if(d2<d1):
p=2
if(d3<d2):
p=3
elif(d3<d1):
p=3
# Calculamos o vetor de variação do estado baseado no ponto mais próximo:
# [dx/dt,dy/dt]=[a,b]
if(p==1):
a=x
b=-0.75*y
elif(p==2):
a=-0.75*(y-2)
b=x-1.5
elif(p==3):
a=0.75*((1.5-x)+(0.5-y))
b=0.25*(x-1.5)
else:
print("Algo deu errado")
m=np.sqrt(a*a+b*b) # Módulo do vetor para normalizar
if(m==0):
m=1
U[l,c]=a/m
V[l,c]=b/m
l=l+1
c=c+1
# Plotamos o resultado
fig, ax = plt.subplots()
ax.quiver(X, Y, U, V) # Os vetores
plt.plot(p1[0],p1[1],'ro') # O ponto de equilíbrio 1
plt.plot(p2[0],p2[1],'go') # O ponto de equilíbrio 2
plt.plot(p3[0],p3[1],'go') # O ponto de equilíbrio 3
plt.show()
Principais materiais utilizados
- Numerical Methods (Instituto de Tecnologia de Massachusetts)
- Numerical Solution of Ordinary Differential Equations (R. Sureshkumar,Instituto de Tecnologia de Massachusetts)
- A estes materiais, somam-se os vistos em Modelo de Lotka-Volterra
Citações
- ↑ Limits and Continuity (Rebecca Noonan-Heale ,Universidade de Utah)
Anterior: Modelo de Lotka-Volterra | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 2 espécies I


![{\displaystyle \lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma uv}{\left[{\frac {\gamma a-kc}{\alpha }}\right]u}}=\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\gamma v}{\left[{\frac {\gamma a-kc}{\alpha }}\right]}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96e69b5a4e9cb6d6848f846bd70accd7415d9d92)