Modelo espacialmente explícito para 2 espécies

Anterior: Modelo de Levins aprimorado para 2 espécies II | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 3 espécies

Em um primeiro momento, é importante lembrar que este modelo foi construído para ser coerente com o contexto ecológico da região norte da Patagônia. Neste modelo, busca-se modelar a interação entre dois herbívoros que competem de forma hierárquica entre si, considerando também a dinâmica de degradação e recuperação do ambiente. Esta dinâmica do ambiente é fruto da interação surgida da competição entre as espécies.

A degradação de um fragmento diz especificamente sobre a quantidade de recursos naturais disponíveis pra a sobrevivência de herbívoros. Os guanacos e as ovelhas são responsáveis por impactar no ambiente, porém como o guanaco evoluiu com a flora, e seu consumo sobre condições naturais permite um consumo sustentável, vamos considerar seu impacto como negligenciável. Assim temos as ovelhas (devido a atividade pecuária humana) sendo responsável pelo impacto ambiental.

Dessa forma temos como principais características do modelo:

$x_{1}\rightarrow$ $x_{1}\rightarrow$ Guanaco, o competir superior:
- Qualquer fragmento que não esteja destruído nem já ocupado por guanacos, está disponível para ocupação pelos primeiros vizinhos ocupados por guanacos com uma probabilidade $c_{1}$ ;
- Podem ser extinto localmente em cada fragmento ocupado com uma probabilidade $e_{1}$ ;

$x_{2}\rightarrow$ $x_{2}\rightarrow$ Ovelha, o competidor inferior:
- Qualquer fragmento que não esteja destruído e nem ocupado por nenhuma espécie está disponível para colonização de ovelhas que ocupam fragmentos primeiros vizinhos com uma probabilidade $c_{2}$
- Pode ser extinta localmente por deslocamento competitivo quando em um mesmo fragmento coexistem com guanacos com uma probabilidade $c_{1}$ ;
- Podem ser extinto localmente em cada fragmento ocupado com uma probabilidade $e_{2}$ .

E por fim, a dinâmica dos fragmentos $h$ :

Quando um fragmento é ocupado por uma ovelha, dispara um relógio interno, após $\tau _{0}$ $\tau _{0}$ passos o fragmento é considerado destruído, e todas as populações ocupando o fragmento são extintas localmente;
- Se a ovelha for extinta localmente antes de atingir $\tau _{0}$ , o relógio interno é zerado.
Após ser considerado destruído, é disparado novamente o relógio interno, e então após $\tau _{r}$ passos o fragmento é considerado disponível novamente

A simulação ocorre em uma grade $L_{x}\times L_{y}$ , onde um fragmento na posição $\left(i,j\right)$ é considerado ocupado pela espécie $\alpha$ se $X_{\alpha }\left(i,j\right)=1$ , de modo análogo, o fragmento é considerado disponível se $h\left(i,j\right)=1$ . Ao final de cada passo calculamos a fração ocupada por cada espécie:

x_{\alpha }={\frac {1}{\left(L_{x}-2\right)\left(L_{y}-2\right)}}\sum _{i,j}X_{\alpha }\left(i,j\right)

Pois as bordas são consideradas permanentemente destruídas. Para $h$ o cálculo é análogo.

Resultados

Comparando o resultado obtido pelo código abaixo com os resultados apresentados originalmente no artigo utilizado como material principal, temos:

À esquerda o gráfico gerado pelo código, e à direita a imagem do artigo original. Os parâmetros com que a simulação foi executada foram

c_{1}=0.05

,

c_{2}=0.5

,

e_{1}=0.05

,

e_{2}=0.01

,

\tau _{r}=50

e

\tau _{o}=17

.

Acima o gráfico gerado pelo código, e abaixo a imagem do artigo original. Os parâmetros com que a simulação foi executada foram

c_{1}=0.05

,

c_{2}=0.7

,

e_{1}=0.05

,

e_{2}=0.01

,

\tau _{r}=50

e

\tau _{o}

conforme indicado.

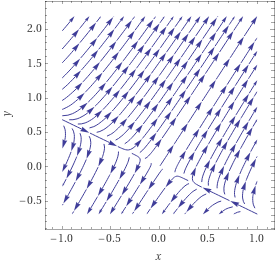
Código

# -*- coding: UTF-8 -*-

# Modelo espacialmente explícito para 2 espécies
# Jhordan Silveira de Borba
# sbjhordan@gmail.com

#Bibliotecas
import numpy as np                                      # Biblioteca de funções matemáticas
import copy                                             # Biblioteca com funções para copiar

#CONDIÇÕES INICIAIS ------------------------------------------------------
maxt = 6000     #tiempo total de cada realizacion
Lx   = 100      #tamaño del sustrato en la coordenada x
Ly   = 100

#Fracciones iniciales
x10  = 0.6  #fraccion inicial de sitios ocupados por x1
x20  = 0.5  #fraccion inicial de sitios ocupados por x2

#Tasas               
cx1   = 0.05         #colonizaciones       
cx2   = 0.5        
ex1   = 0.05         #extinciones       
ex2   = 0.01      
to    = 50           #Período de ocupação
tr    = 17           #Período de recuperação

#Inicializaciones
c =  np.full((Lx, Ly), [0])   # Relógio interno
s  = np.full((Lx, Ly), [1])   # matriz de habitat (1=sitio disponible, 0=destruido)
x1 = np.full((Lx, Ly), [0])   # 1 = sitio ocupado, 0 sitio vazio
x2 = np.full((Lx, Ly), [0])   # 1 = sitio ocupado, 0 sitio vazio

# Destruimos los bordes del habitat
for i in range(Lx): 
  s[i,0]=0
  s[i,Ly-1]=0
for j in range(Ly):
  s[0,j]=0
  s[Lx-1,j]=0

# Distribui a população inicial de herbívoros
for i in range(1,Lx-1): 
  for j in range (1,Ly-1): 
    rnd=np.random.rand()
    if (rnd < x10 and s[i,j]==1): x1[i,j]=1
    rnd=np.random.rand()
    if (rnd < x20 and s[i,j]==1): x2[i,j]=1

#-------------------------------------------------------
#Lazo temporal
fx1=sum(sum(x1))/((Lx-2)*(Ly-2))
fx2=sum(sum(x2))/((Lx-2)*(Ly-2))
fs =sum(sum(s)) /((Lx-2)*(Ly-2))
f = open("temporal2019.dat", "w")
f.write("	"+str(0)+"	"+str(fx1)+"	"+str(fx2)+"	"+str(fs)+"\n")

for it in range(maxt):
  if (float(it)%(float(maxt)/100)==0.):
    print("Porcentagem: "+str(it*100/maxt))  # Exibe o passo atual
    
  sold=copy.copy(s)                # Distribuição de fragmentos do passo anterior
  x1old=copy.copy(x1)              # Poblaciones del paso anterior
  x2old=copy.copy(x2)
  
  #Recorro la malla 
  for i in range (1,Lx-1):
    for j in range (1,Ly-1):
        
      #Colonizaciones
      if (x1old[i,j]==0 and s[i,j]==1):                           #colonizacion de x1 si el sitio esta libre de x1 y no destruido:
        nvec=x1old[i-1,j]+x1old[i+1,j]+x1old[i,j-1]++x1old[i,j+1] #cantidad de vecinos ocupados
        p=1.0-(1.0-cx1)**nvec                                     #probabilidad de ser colonizado= 1 - prob de quedar libre
        rnd=np.random.rand() 
        if (rnd < p):x1[i,j]=1
      
      if (x2old[i,j]==0 and s[i,j]==1 and x1old[i,j]==0):         #colonizacion de x2 si el sitio esta libre de x1 y x2, y no destruido: 
        nvec=x2old[i-1,j]+x2old[i+1,j]+x2old[i,j-1]+x2old[i,j+1]  #cantidad de vecinos ocupados
        p=1.0-(1.0-cx2)**nvec                                     #probabilidad de ser colonizado= 1 - prob de quedar libre 
        rnd=np.random.rand()
        if (rnd < p): x2[i,j]=1                                

      #extinciones
      if (x1old[i,j]==1):                          #extincion de x1 si el sitio esta ocupado 
        rnd=np.random.rand()
        if (rnd < ex1): x1[i,j]=0

      if (x2old[i,j]==1):                          #extincion de x2 si el sitio esta ocupado 
        rnd=np.random.rand()
        if (rnd < ex2): 
            x2[i,j]=0
            c[i,j]=0 

      #desplazamiento por competencia (jerarquia)
      if (x1old[i,j]==1 and x2old[i,j]==1):
        rnd=np.random.rand()
        if (rnd < cx1): 
            x2[i,j]=0
            c[i,j]=0
            
      #Atualização dos relógios internos
      if (x2old[i,j]==1):   # Se está ocupado por ovelhas
          c[i,j]=c[i,j]+1   # Avança o relógio interno
          if (c[i,j]==to):  # Se agintiu o período máximo de ocupação
              c[i,j]=0      # Exingue todas espécies e reseta o relógio, e torna o fragmento indisponível
              s[i,j]=0
              x1[i,j]=0
              x2[i,j]=0
      elif (sold[i,j]==0):  # Se está destruído
          c[i,j]=c[i,j]+1   # Avança o relógio intenro
          if (c[i,j]==tr):  # Se atingiu o período de recuperação
              c[i,j]=0      # REseta o relógio e torna o fragmento disponível
              s[i,j]=1
  
  fx1=sum(sum(x1))/((Lx-2)*(Ly-2))
  fx2=sum(sum(x2))/((Lx-2)*(Ly-2))
  fs =sum(sum(s)) /((Lx-2)*(Ly-2))
  f.write("	"+str(it+1)+"	"+str(fx1)+"	"+str(fx2)+"	"+str(fs)+"\n")
 
f.close

Principal material utilizado

Waves of desertification in a competitive ecosystem (Y. C. Daza C. e outros, Ecological Modelling)

Anterior: Modelo de Levins aprimorado para 2 espécies II | Índice: Ecologia | Próximo: Modelo de Levins aprimorado para 3 espécies

Modelo espacialmente explícito para 2 espécies

Resultados

Código

Principal material utilizado

Menu de navegação

Pesquisa