Modelo de Levins aprimorado para 2 espécies

Anterior: Modelo de Lotka-Volterra amortecido | Índice: Ecologia | Próximo: Modelo espacialmente explícito

Comparação com outros modelos

Para duas espécies, vamos trabalhar com o seguinte sistema de equações:

${\begin{aligned}{\frac {dx}{dt}}=&c_{1}x\left(1-D-x\right)-e_{1}x-\mu xy\\{\frac {dy}{dt}}=&yc_{y}\left(x-yx\right)-ye_{y}\\\end{aligned}}$

Onde $x$ é a presa e $y$ o predador. Podemos comparar com outros modelos. Como um modelo inspirado no modelo de Levins, podemos ver semelhanças bastante fortes desde já. Lembrando do modelo de Levins rapidamente:

${\frac {dp}{dt}}=c\left(h-p\right)p-ep$

O termo $\left(1-D-x\right)$ na equação da presa é a quantidade de fragmentos disponíveis para a colonização da presa, uma vez que precisamos descontar os fragmentos destruídos, além dos ocupados. Como todos parâmetros são em termos de proporções, temos probabilidade de selecionarmos um fragmento disponível para a colonização da presa. E o termo $\left(x_{1}-yx_{1}\right)$ na equação do predador tem a mesma função, porém agora precisamos lembrar que os fragmentos que o predador pode ocupar são os que já estão ocupados pela presa, descontando os que já possuem predador. Então considerando propriedades de conjuntos, e olhando em termos de probabilidades esta equação, temos a probabilidade $P\left(x\right)$ de selecionar um fragmento ocupada pela presa, mas precisamos descontar a probabilidade de selecionar um fragmento que também já esteja ocupada por um predador $P\left(x\cap y\right)$. A maior diferença se dá porque a presa tem um termo a mais correspondendo ao decréscimo da população devido a predação, evento não considerado no modelo de Levins, mas considerado no modelo de Lotka-Volterra.

Por isso a próxima comparação que podemos fazer é com o modelo de Lotka-Volterra amortecido:

${\begin{aligned}{\frac {dx}{dt}}=&x\left(a-\alpha y\right)-kx^{2}\\{\frac {dy}{dt}}=&y\left(-c+\gamma x\right)\\\end{aligned}}$

Vamos reescrever nosso sistema de equações:

${\begin{aligned}{\frac {dx}{dt}}=&x\left(c_{1}\left(1-D\right)-\mu y\right)-c_{1}x^{2}-e_{1}x\\{\frac {dy}{dt}}=&y\left(-e_{y}+c_{y}x\right)-c_{y}xy^{2}\\\end{aligned}}$

Olhando agora primeiro para a equação da presa, a maior diferença que encontramos, e é que temos o termo de extinção local que não é devido a predação $e_{1}x$, algo já familiar do modelo de Levins. E já quando olhamos para a equação do predador, temos o termo ${\textstyle \left(c_{y}x\right)y^{2}}$ , podemos pensar também como um termo logístico, impondo um limite na população de predadores, da mesma forma que ocorre com as presas. Porém agora o termo logístico não é uma constante, mas depende também da população de presas.

Análises dos pontos de equilíbrio

Sendo todos o parâmetros como variáveis

Vamos tentar fazer análises parecidas agora. Primeiro buscar os pontos de equilíbrio pro sistema:

$${\begin{array}{cc}x\left[\left(c_{1}\left(1-D\right)-\mu y\right)-c_{1}x-e_{1}\right]&=0\\y\left[\left(-e_{y}+c_{y}x\right)-c_{y}xy\right]&=0\end{array}}$$

Temos então 4 pontos de equilíbrio:

• Primeiro: ${\textstyle \left(0,0\right)\rightarrow }$ extinção de ambas as espécies
• Segundo: ${\textstyle \left(\left(1-D\right)-{\frac {e_{1}}{c_{1}}},0\right)\rightarrow }$ extinção do predador

Os pontos de equilíbrio com ambas as espécies são extremamente mais complicados. Para o terceiro ponto temos:

$${\begin{array}{cc}x=&-{\frac {{\sqrt {c_{y}^{2}\mu ^{2}+\left(4c_{1}c_{y}e_{y}+2c_{y}^{2}e_{1}+\left(2D-2\right)c_{1}c_{y}^{2}\right)\mu +c_{y}^{2}e_{1}^{2}+\left(2D-2\right)c_{1}c_{y}^{2}e_{1}+\left(D^{2}-2D+1\right)c_{1}^{2}c_{y}^{2}}}+c_{y}\mu +c_{y}e_{1}+\left(D-1\right)c_{1}c_{y}}{2c_{1}c_{y}}}\\y=&{\frac {{\sqrt {c_{y}^{2}\mu ^{2}+\left(4c_{1}c_{y}e_{y}+2c_{y}^{2}e_{1}+\left(2D-2\right)c_{1}c_{y}^{2}\right)\mu +c_{y}^{2}e_{1}^{2}+\left(2D-2\right)c_{1}c_{y}^{2}e_{1}+\left(D^{2}-2D+1\right)c_{1}^{2}c_{y}^{2}}}+c_{y}\mu -c_{y}e_{1}+\left(1-D\right)c_{1}c_{y}}{2c_{y}\mu }}\end{array}}$$

E o quarto e último ponto:

$${\begin{array}{cc}x=&{\frac {{\sqrt {c_{y}^{2}\mu ^{2}+\left(4c_{1}c_{y}e_{y}+2c_{y}^{2}e_{1}+\left(2D-2\right)c_{1}c_{y}^{2}\right)\mu +c_{y}^{2}e_{1}^{2}+\left(2D-2\right)c_{1}c_{y}^{2}e_{1}+\left(D^{2}-2D+1\right)c_{1}^{2}c_{y}^{2}}}-c_{y}\mu -c_{y}e_{1}-\left(D-1\right)c_{1}c_{y}}{2c_{1}c_{y}}}\\y=-&{\frac {{\sqrt {c_{y}^{2}\mu ^{2}+\left(4c_{1}c_{y}e_{y}+2c_{y}^{2}e_{1}+\left(2D-2\right)c_{1}c_{y}^{2}\right)\mu +c_{y}^{2}e_{1}^{2}+\left(2D-2\right)c_{1}c_{y}^{2}e_{1}+\left(D^{2}-2D+1\right)c_{1}^{2}c_{y}^{2}}}-c_{y}\mu +c_{y}e_{1}-\left(1-D\right)c_{1}c_{y}}{2c_{y}\mu }}\end{array}}$$

Estes últimos pontos (com o equilíbrio entre as espécies) são complicados demais para nos referirmos explicitamente daqui em diante quando necessário utilizamos alguma notação como ${\textstyle \left(x_{j},y_{j}\right)}$ para denotar o ${\textstyle j-{\acute {e}}simo}$ ponto de equilíbrio, sem escrevê-lo por inteiro. Vamos linearizar e analisar a estabilidade em torno dos pontos de equilíbrio. Para o ponto ${\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}$ é muito simples:

$${\frac {dx}{dt}}=x\left(c_{1}\left(1-D\right)-\mu y\right)-c_{1}x^{2}-e_{1}x$$

$${\frac {dy}{dt}}=y\left(-e_{y}+c_{y}x\right)-c_{y}xy^{2}$$

Separando os termos lineares dos não lineares:

$${\frac {dx}{dt}}=\left[x\left(c_{1}\left(1-D\right)-e_{1}\right)\right]-\left[\mu yx+c_{1}x^{2}\right]$$

$${\frac {dy}{dt}}=-\left[ye_{y}\right]+\left[c_{y}xy-c_{y}xy^{2}\right]$$

Calculando então os limites:

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\mu yx+c_{1}x^{2}}{x\left(c_{1}\left(1-D\right)-e_{1}\right)}}=\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {\mu y+c_{1}x}{c_{1}\left(1-D\right)-e_{1}}}=0$$

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {c_{y}xy-c_{y}xy^{2}}{ye_{y}}}=\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}-{\frac {c_{y}x-c_{y}xy}{e_{y}}}=0$$

Desprezando os termos não lineares:

$$\left({\begin{array}{c}{\dot {x}}\\{\dot {y}}\end{array}}\right)=\left({\begin{array}{cc}c_{1}\left(1-D\right)-e_{1}&0\\0&-e_{y}\end{array}}\right)\left({\begin{array}{c}x\\y\end{array}}\right)$$

Logo um dos autovalores é real, sempre negativo ${\textstyle \left(-e_{y}\right)}$ e o segundo é ${\textstyle \left(c_{1}\left(1-D\right)-e_{1}\right)}$. Basicamente se o termo de colonização do guanaco for maior que o da extinção ${\textstyle \left(c_{1}\left(1-D\right)>e_{1}\right)}$, temos dois autovalores de sinais opostos, ou seja, um ponto de instabilidade. Aumentando a taxa de extinção do guanaco (ou a destruição do habitat) passamos a ter ${\textstyle c_{1}\left(1-D\right)<e_{1}}$, e a extinção de ambas as espécies. Aqui podemos notar uma diferença dos modelos de Lotka-Volterra: a extinção de ambas as espécies pode ser um ponto de equilíbrio estável. Ou seja nos modelos anteriores o sistema nunca iria para o equilíbrio com extinção total, agora há essa possibilidade dependendo do nível de destruição do sistema.

Para o segundo ponto de equilíbrio ${\textstyle \left(x_{2},y_{2}\right)=\left(x_{2},0\right)}$ precisamos fazer a translação: ${\textstyle u=x-x_{2}}$ e ${\textstyle v=y}$.

$${\frac {du}{dt}}=\left[\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)u+\left(-\mu x_{2}\right)v+\left(-c_{1}x_{2}^{2}-e_{1}x_{2}+\left(1-D\right)x_{2}c_{1}\right)\right]+\left[-\mu uv-c_{1}u^{2}\right]$$

$${\frac {dv}{dt}}=\left[\left({\it {c_{y}}}x_{2}-{\it {e_{y}}}\right)v\right]+\left[-{\it {c_{y}}}v^{2}x_{2}-{\it {c_{y}}}uv^{2}+{\it {c_{y}}}uv\right]$$

Podemos ver facilmente que é semi linear para ${\textstyle {\dot {u}}}$ uma vez que ao fazermos os:

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}{\frac {\text{parte não-linear}}{\text{parte linear}}}$$

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {-\mu uv-c_{1}u^{2}}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)u+\left(-\mu x_{2}\right)v}}$$

Fazendo a substituição ${\textstyle r^{2}=x^{2}+y^{2}}$ e ${\textstyle \left(x,y\right)=\left(r\cos \theta ,r\sin \theta \right)}$:

$$\lim _{r\rightarrow 0}{\frac {r^{2}\left(-\mu \cos \theta \sin \theta -c_{1}\cos \theta ^{2}\right)}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)r\cos \theta +\left(-\mu x_{2}\right)r\sin \theta }}$$

$$\lim _{r\rightarrow 0}{\frac {r\left(-\mu \cos \theta \sin \theta -c_{1}\cos \theta ^{2}\right)}{\left(-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}\right)\cos \theta +\left(-\mu x_{2}\right)\sin \theta }}=0$$

É interessante notar que a parte constante vai zerar. E para ${\textstyle {\dot {v}}}$:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {\left[-{\it {c_{y}}}v^{2}x_{2}-{\it {c_{y}}}uv^{2}+{\it {c_{y}}}uv\right]}{\left[\left({\it {c_{y}}}x_{2}-{\it {e_{y}}}\right)v\right]}}={\frac {\left[-{\it {c_{y}}}vx_{2}-{\it {c_{y}}}uv+{\it {c_{y}}}u\right]}{\left[\left({\it {c_{y}}}x_{2}-{\it {e_{y}}}\right)\right]}}=0$$

Analisando o comportamento linear então na proximidade do ponto de equilíbrio:

$$\left({\begin{array}{c}{\dot {u}}\\{\dot {v}}\end{array}}\right)=\left({\begin{array}{cc}-2c_{1}x_{2}+\left(1-D\right)c_{1}-e_{1}&-\mu x_{2}\\0&{\it {c_{y}}}x_{2}-{\it {e_{y}}}\end{array}}\right)\left({\begin{array}{c}u\\v\end{array}}\right)$$

E os autovalores são então:

• ${\textstyle \lambda _{1}=\left(1-D-{\frac {e_{1}}{c_{1}}}\right)c_{y}-e_{y}}$
• ${\textstyle \lambda _{2}=e_{1}-\left(1-D\right)c_{1}}$

Podemos ver que o segundo autovalor tem uma relação entre a extinção e a colonização dos guanacos, se tivermos um valor suficientemente alto de colonização então ${\textstyle \left(1-D\right)c_{1}>e_{1}\rightarrow \lambda _{2}<0}$ . E no primeiro autovalor temos uma relação entre a colonização e morte de predadores, se a morte de predadores for suficientemente alta ${\textstyle e_{y}>\left(1-D-{\frac {e_{1}}{c_{1}}}\right)c_{y}}$ então ${\textstyle \lambda _{1}<0}$ . Com as duas condições satisfeitas, temos um ponto de equilíbrio onde os predadores são extintos, e só restam presas.

E por fim, temos dois pontos que suportam a coexistência entre duas espécies. Para ${\textstyle \left(x_{3},y_{3}\right)}$:

$${\frac {du}{dt}}={\begin{array}{c}\left[\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)u+\left(-\mu x_{3}\right)v+\left(-\mu x_{3}y_{3}-c_{1}x_{3}^{2}-e_{1}x_{3}+\left(1-D\right)c_{1}x_{3}\right)\right]+\\\left[-\mu uv-c_{1}u^{2}\right]\end{array}}$$

$${\frac {dv}{dt}}={\begin{array}{c}\left[\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)u+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)v+\left(c_{y}x_{3}y_{3}-y_{3}^{2}c_{y}x_{3}-e_{y}y_{3}\right)\right]+\\\left[-2c_{y}uvy_{3}-c_{y}v^{2}x_{3}-c_{y}uv^{2}+c_{y}uv\right]\end{array}}$$

Calculando os limites para verificar o comportamento semi linear:

$$\lim _{\left(x,y\right)\rightarrow \left(0,0\right)}{\frac {\text{parte não-linear}}{\text{parte linear}}}$$

Para ${\textstyle {\dot {u}}}$:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {-\mu uv-c_{1}u^{2}}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)u+\left(-\mu x_{3}\right)v}}$$

$$\lim _{r\rightarrow 0}{\frac {r^{2}\left(-\mu \cos \theta \sin \theta -c_{1}\cos ^{2}\theta \right)}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)r\cos \theta +\left(-\mu x_{3}\right)r\sin \theta }}$$

$$\lim _{r\rightarrow 0}{\frac {r\left(-\mu \cos \theta \sin \theta -c_{1}\cos ^{2}\theta \right)}{\left(\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}\right)\cos \theta +\left(-\mu x_{3}\right)\sin \theta }}=0$$

E para ${\textstyle {\dot {v}}}$:

$$\lim _{\left(u,v\right)\rightarrow \left(0,0\right)}{\frac {-2c_{y}uvy_{3}-c_{y}v^{2}x_{3}-c_{y}uv^{2}+c_{y}uv}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)u+\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)v}}$$

$$\lim _{r\rightarrow 0}{\frac {r^{2}\left(-2c_{y}\cos \theta \sin \theta y_{3}-c_{y}\sin ^{2}\theta x_{3}-c_{y}\cos \theta \sin ^{2}\theta +c_{y}\cos \theta \sin \theta \right)}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)r\cos \theta +\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)r\sin \theta }}$$

$$\lim _{r\rightarrow 0}{\frac {r\left(-2c_{y}\cos \theta \sin \theta y_{3}-c_{y}\sin ^{2}\theta x_{3}-c_{y}\cos \theta \sin ^{2}\theta +c_{y}\cos \theta \sin \theta \right)}{\left(c_{y}y_{3}-y_{3}^{2}c_{y}\right)\cos \theta +\left(c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\right)\sin \theta }}=0$$

Montando a matriz linearizada então:

$$\left({\begin{array}{c}{\dot {u}}\\{\dot {v}}\end{array}}\right)=\left({\begin{array}{cc}\left(1-D\right)c_{1}-e_{1}-2c_{1}x_{3}-\mu y_{3}&-\mu x_{3}\\c_{y}y_{3}-y_{3}^{2}c_{y}&c_{y}x_{3}-e_{y}-2c_{y}x_{3}y_{3}\end{array}}\right)\left({\begin{array}{c}u\\v\end{array}}\right)$$

Infelizmente o autovalor é extremamente complexo se vamos considerar todos os parâmetros como variáveis. A partir de agora, vamos trabalhar atribuindo valores numéricos aos parâmetros, exceto o fato de destruição do habitat, que é um parâmetro que estamos interessado em analisar como afeta a dinâmica.

Caso particular 1: Utilizando os parâmetros do artigo

Utilizando o seguinte conjunto de parâmetros

• ${\textstyle c_{1}=0.1}$
• ${\textstyle e_{1}=0.025}$
• ${\textstyle e_{y}=0.015}$
• ${\textstyle \mu =0.3}$
• ${\textstyle c_{y}=0.015}$

Temos os seguintes pontos de equilíbrio com os respectivos autovalores:

• ${\textstyle \left(x_{1},y_{1}\right)=\left(0,0\right)}$
  • ${\textstyle \lambda _{1,k}\in \left\{-{\frac {3}{200}},{\frac {\left(0.75-D\right)}{10}}\right\}}$
• ${\textstyle \left(x_{2},y_{2}\right)=\left(0.75-D,0\right)}$
  • ${\textstyle \lambda _{2,k}\in \left\{-{\frac {12D+3}{800}},{\frac {\left(D-0.75\right)}{10}}\right\}}$
• ${\textstyle \left(x_{3},y_{3}\right)=\left({\frac {-4D-9-{\sqrt {16D^{2}+72D+273}}}{8}},{\frac {-4D+\left({\sqrt {16D^{2}+72D+273}}+15\right)}{24}}\right)}$
  • ${\textstyle \lambda _{3,1}={\frac {23{\sqrt {16D^{2}+72D+273}}+92D+231-{\sqrt {2}}{\sqrt {\left(1156D+1233\right){\sqrt {16D^{2}+72D+273}}+4624D^{2}+23016D+33369}}}{3200}}}$
  • ${\textstyle \lambda _{3,2}={\frac {23{\sqrt {16D^{2}+72D+273}}+92D+231+{\sqrt {2}}{\sqrt {\left(1156D+1233\right){\sqrt {16D^{2}+72D+273}}+4624D^{2}+23016D+33369}}}{3200}}}$
• ${\textstyle \left(x_{4},y_{4}\right)=\left({\frac {-4D-9+{\sqrt {16D^{2}+72D+273}}9}{8}},{\frac {-4D-\left({\sqrt {16D^{2}+72D+273}}+15\right)}{24}}\right)}$
  • ${\textstyle \lambda _{4,1}={\frac {-23{\sqrt {16D^{2}+72D+273}}+92D+231-{\sqrt {2}}{\sqrt {\left(-1156D-1233\right){\sqrt {16D^{2}+72D+273}}+4624D^{2}+23016D+33369}}}{3200}}}$
  • ${\textstyle \lambda _{4,2}={\frac {-23{\sqrt {16D^{2}+72D+273}}+92D+231+{\sqrt {2}}{\sqrt {\left(-1156D-1233\right){\sqrt {16D^{2}+72D+273}}+4624D^{2}+23016D+33369}}}{3200}}}$

Para o primeiro ponto ele está fixo ${\textstyle \left(0,0\right)}$ e podemos perceber que um autovalor é negativo e o outro depende se ${\textstyle D}$ é maior ou menor que ${\textstyle 0.75}$. Para fatores de destruição maior, ambos autovalores são negativos e temos um ponto de equilíbrio estável com a extinção de ambas espécies, para fatores de destruição menor, temo um ponto instável.

Para o segundo ponto de equilíbrio, temos novamente uma dependência da relação entre ${\textstyle D}$ e ${\textstyle 0.75}$. O próprio pronto vai se aproximando a ${\textstyle \left(0,0\right)}$ conforme ${\textstyle D}$ cresce. Além disso para valores em que ${\textstyle D<0.75}$ temos um ponto de equilíbrio estável e para acima deste valores se torna instável. Lembrando que para ${\textstyle D>0.75}$ o ponto já passa a ter uma população negativa de pumas, o que não faz sentido ecologicamente, enquanto o primeiro ponto de equilíbrio ${\textstyle \left(0,0\right)}$ se torna estável. Então “recuperamos”o resultado do primeiro ponto de equilíbrio.

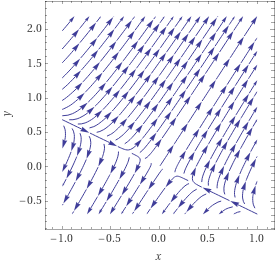
Os próximos como pode-se imaginar são mais complicados de se analisar, por isso vamos utilizar gráficos para trabalhar.

Os gráfico superiores fazem referência ao terceiro ponto de equilíbrio, e os inferiores o quarto ponto. À esquerda a localização do ponto de equilíbrio, e à direita os autovalores.

Podemos ver que nos dois pontos de equilíbrio temos uma população negativa, e um auto valor positivo, portanto são pontos que não fazem sentido ecologicamente e matematicamente são pontos de equilíbrio instável.

Caso particular 2: Fatores de colonização aumentados

Análogo ao problema do modelo de Levins, este modelo ainda carrega a deficiência de não considerar a configuração espacial. Vamos analisar outro cenário que damos multiplicamos por 4 as taxas de colonização, com o objetivo de analisarmos um cenário em que há coexistência entre presas epredadores.

Repetindo os cálculos temos que o primeiro ponto de equilíbrio é ${\textstyle \left(0,0\right)}$, com os autovalores ${\textstyle \left(-{\frac {3}{200}},{\frac {16}{40}}\left(0.9375-D\right)\right)}$, então agora para ${\textstyle D<0.9375}$, este é um ponto de equilíbrio instável. O segundo ponto de equilíbrio é ${\textstyle \left(D-0.9375,0\right)}$ com os autovalores ${\textstyle \left({\frac {48}{800}}\left(0.6875-D\right),{\frac {16}{40}}\left(D-0.9375\right)\right)}$, então para ${\textstyle D<0.6875}$ temos temos o par de sinai dos autovalores ${\textstyle \left(+,-\right)}$ , para valores maiores que ${\textstyle D>0.9375}$ ${\textstyle \left(-,+\right)}$ e para valores intermediários ${\textstyle 0.6875<D<0.9375}$ temos ${\textstyle \left(-,-\right)}$. O que isso significa?

Bom, para valores maiores que ${\textstyle 0.9375}$ então temos um ponto de equilíbrio instável,e nessa situação o ponto estável é em ${\textstyle \left(0,0\right)}$ ou seja, esperamos o a extinção de de ambas as espécies. Para valores entre ${\textstyle 0.6875<D<0.9375}$ temos um ponto de equilíbrio estável, nessa situação, apenas a presa sobrevive. E para valores menores, temos um ponto de equilíbrio instável. E esperamos que os próximos dois pontos de equilíbrio nos ajude a responder o que acontece. Semelhante à discussão anterior, os próximos dois pontos são melhores analisados através de gráficos.

Análise do terceiro ponto de equilíbrio. À esquerda a psição do ponto e a direita seu auto-valor.

Para o terceiro ponto de equilíbrio, sempre temos população de presas negativas, o que não fez sentido ecologicamente. Esse resultadoé coerente matematicamente pois a parte real dos autovalores são sempre positivos, então é um ponto instável. E por fim, o mais interessante é o quarto ponto de equilíbrio. Para este ponto, ${\textstyle D=0.6875}$ é exatamente o valor no qual deixa de ser um ponto que ecologicamente faz sentido e também deixa de ser um ponto de equilíbrio estável, e para valores menores que este, tempos um ponto de equilíbrio estável. Então resumidamente, temos

Análise do quarto ponto de equilíbrio. À esquerda a psição do ponto e a direita seu auto-valor.

• ${\textstyle D<0.6875}$: Coexistência de ambas espécies;
• ${\textstyle 0.6875<D<0.9375}$: Sobrevivência da presa;
• ${\textstyle 0.9375<D}$: Extinção de todas as espécies.

Plotando então a evolução e diagramas de fases para 3 valores de ${\textstyle D}$ (${\textstyle 0.5,0.7,0.96}$), temos:

Na esquerda superior temos o espaço de fase plotado via Python para os diferentes valoresde $D$. As outras três imagens são os diagramas de fases pltoas via WolframAlpha para os três diferentes valos de $D$.

Códigos

Script para o WxMaxima utilizado para efetuar os cálculos simbólicos necessários para analisar os pontos de equilíbrio considerando todos parâmetros como variáveis:

Cálculos simbólico do modelo de Levins aprimorado para 2 espécies considerando todos parâmetros como variáveis
Jhordan Silveira de Borba
sbjhordan@gmail.com
 -->	ratprint: false$
Declaração do sistema de equações:
 -->	dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x);
	dy:(y*(-e_y+c_y*x)-c_y*x*y^2);
Soluções e verificação das soluções
 -->	sol:(algsys([dx, dy], [x,y]));
	N:1;radcan(dx),sol[N][1],sol[N][2]; radcan(dy),sol[N][1],sol[N][2];
Segundo ponto:
	- Deslocamento
	- Verificação que a solução linear tem o mesmo ponto de equilíbrio e autovalor
	    - Aqui se a partir de A2 tivermos x_2=x, então x é a posição do ponto de equilíbrio, e não uma variável.
 -->	radcan(dx),x=u+x_2,y=v;radcan(dy),x=u+x_2,y=v;
 -->	B:matrix([u],[v]);
	A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x;
	C2:matrix([-c_1*x_2^2-e_1*x_2+(1-D)*x_2*c_1],[0]),x_2=x;
	radcan(A2.B),u=0,v=0,sol[2][1];
	radcan(C2),u=0,v=0,sol[2][1];
	radcan(eigenvalues(A2)),sol[2][1];
Terceiro e quarto ponto ponto:
	- Deslocamento
	- Verificação que a solução linear tem o mesmo ponto de equilíbrio e autovalor
	    - Aqui se a partir de A3 tivermos x_3=x e y_3=y, então x e y são a posição do ponto de
	equilíbrio, e não uma variável.
 -->	radcan(dx),x=u+x_3,y=v+y_3;radcan(dy),x=u+x_3,y=v+y_3;
 -->	A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y;
	C3:matrix([-mu*x_3*y_3-c_1*x_3^2-e_1*x_3+(1-D)*c_1*x_3],[c_y*x_3*y_3-y_3^2*c_y*x_3-e_y*y_3]),x_3=x,y_3=y;
	radcan(A3.B),u=0,v=0,sol[3][1],sol[3][2];
	radcan(C3),u=0,v=0,sol[3][1],sol[3][2];
	radcan(C3),u=0,v=0,sol[4][1],sol[4][2];
	radcan(eigenvalues(A3)),sol[3][1],sol[3][2];

Script para calcularmos os pontos de equilíbrio e autovalores do sistema tendo a fração de destruição do sistema como única variável:

Análise utilizando como variável apenas D
Jhordan Silveira de Borba 
sbjhordan@gmail.com

- Repetimos todos os cálculos substituindo as variáveis pelos valores
- Plotamos os gráficos
- Obs.: Para obtermos a parte real usamos realpart(%) e a imaginária
imagpart(%) 
-->	c_1:0.1;e_1:0.025;e_y:0.015;mu:0.3;c_y:0.015;
	dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x);
	dy:(y*(-e_y+c_y*x)-c_y*x*y^2);
	sol:(algsys([dx, dy], [x,y]));
	B:matrix([u],[v]);
	A1:matrix([c_1*(1-D)-e_1,0],[0,-e_y]);
	A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x;
	A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y;
	l1:radcan(eigenvalues(A1));
	l2:radcan(eigenvalues(A2)),sol[2][1];
	l3:radcan(eigenvalues(A3)),sol[3][1],sol[3][2];
	l4:radcan(eigenvalues(A3)),sol[4][1],sol[4][2];
 -->	X:x,sol[3][1];Y:y,sol[3][2];
	wxplot2d([X,Y], [D,0,1],[legend,"x","y"]);
	wxplot2d([l3[1][1],l3[1][2]], [D,0,1]);
	X:x,sol[4][1];Y:y,sol[4][2]; 
	wxplot2d([X,Y], [D,0,1],[legend,"x","y"]); 
	wxplot2d([l4[1][1],l4[1][2]], [D,0,1]);

Script para calcularmos os vetores em torno de cada ponto de equilíbrio, para que possamos fazer um rascunho do plano de fase.

Calculo de  vetores para o rascunho do plano de fase com D=0.1:
Jhordan Silveira de Borba
 -->	D:0.1;c_1:0.1;e_1:0.025;e_y:0.015;mu:0.3;c_y:0.015;
	dx:(x*(c_1*(1-D)-mu*y)-c_1*x^2-e_1*x);
	dy:(y*(-e_y+c_y*x)-c_y*x*y^2);
	sol:(algsys([dx, dy], [x,y])),numer;
	B:matrix([u],[v]);
	A1:matrix([c_1*(1-D)-e_1,0],[0,-e_y]);
	A2:matrix([-2*c_1*x_2+(1-D)*c_1-e_1,-mu*x_2],[0,c_y*x_2-e_y]),x_2=x;
	C2:matrix([-c_1*x_2^2-e_1*x_2+(1-D)*x_2*c_1],[0]),x_2=x;
	A3:matrix([(1-D)*c_1-e_1-2*c_1*x_3-mu*y_3,-mu*x_3],[c_y*y_3-y_3^2*c_y,c_y*x_3-e_y-2*c_y*x_3*y_3]),x_3=x,y_3=y;
	C3:matrix([-mu*x_3*y_3-c_1*x_3^2-e_1*x_3+(1-D)*c_1*x_3],[c_y*x_3*y_3-y_3^2*c_y*x_3-e_y*y_3]),x_3=x,y_3=y;
	l1:radcan(eigenvalues(A1)),numer;
	l2:radcan(eigenvalues(A2)),sol[2][1],numer;
	l3:radcan(eigenvalues(A3)),sol[3][1],sol[3][2],numer;
	l4:radcan(eigenvalues(A3)),sol[4][1],sol[4][2],numer;
 -->	radcan((A1.B));
	radcan((A2.B)),sol[2][1];
	radcan((A3.B)),sol[3][1],sol[3][2];
	radcan((A3.B)),sol[4][1],sol[4][2];

Script em Python para plotar o rascunho do diagrama de fases, pode ser editado para visualizarmos só a vizinhança de cada ponto.

# -*- coding: utf-8 -*-
# Modelo aprimorado de Levins para 2 espécies: Diagrama de fases
# Jhordan Silveira de Borba
# sbjhordan@gmail.com

import matplotlib.pyplot as plt
import numpy as np


def phase_lot():
    p1=[0.,0.]                                    # Ponto de equilíbrio 1
    p2=[0.65,0.]                                  # Ponto de equilíbrio 2 
    p3=[-3.27,1.31]                               # Ponto de equilíbrio 3 
    p4=[0.92,-0.09]                               # Ponto de equilíbrio 4
    
    X = np.arange(0,1, 0.1/2)                     # Eixo X
    Y = np.arange(0,1, 0.1/2)                     # Eixo Y
    U,V=np.meshgrid(X,Y)
        
    c=0
    for x in X:
        l=0
        for y in Y:
            #Distâncias
            d=[]
            d.append(np.sqrt((x-p1[0])*(x-p1[0])+(y-p1[1])*(y-p1[1])))
            d.append(np.sqrt((x-p2[0])*(x-p2[0])+(y-p2[1])*(y-p2[1])))
            d.append(np.sqrt((x-p3[0])*(x-p3[0])+(y-p3[1])*(y-p3[1])))
            d.append(np.sqrt((x-p4[0])*(x-p4[0])+(y-p4[1])*(y-p4[1])))
            for i in range(len(d)):
                if (min(d)==d[i]):
                    p=i
            
            #Calculamos o vetor baseado no ponto mais próximo:
            if(p==0):
                u=x-p1[0]
                v=y-p1[1]
                a=(13*u)/200
                b=-(3*v)/200               
            elif (p==1):
                u=x-p2[0]
                v=y-p2[1]
                a=-(70*v+23*u+25)/36
                b=-(21*v)/40 
            elif(p==2):
                u=x-p3[0]
                v=y-p3[1]                                       
                a=(285*v+80*u-5)/29
                b=(11*v-10*u)/17
            elif(p==3):
                u=x-p4[0]
                v=y-p4[1]                                       
                a=-(47*v+15*u+12)/17
                b=(20*v-21*u-66)/18
            else:
                print("Algo deu errado")

            m=np.sqrt(a*a+b*b) 		 # Módulo do vetor
            if(m==0):
                m=1
	    # Normalizamos e salvamos o vetor: [dx/dt,dy/dt]=[a,b]
            U[l,c]=a/m
            V[l,c]=b/m
            l=l+1
        c=c+1
    
    fig, ax = plt.subplots()
    ax.quiver(X, Y, U, V)
    plt.plot(p0[0],p0[1],'ko') #Plotamos o primeiro ponto de equilíbrio
    plt.plot(p1[0],p1[1],'ko') #Plotamos o segundo ponto de equilíbrio
    plt.plot(p3[0],p2[1],'ko') #Plotamos o terceiro ponto de equilíbrio
    plt.plot(p4[0],p3[1],'ko') #Plotamos o quarto ponto de equilíbrio
    plt.show()

Script em Python para analisar a evolução do sistema no espaço de fases, utilizando o método de Euler:

# -*- coding: utf-8 -*-
# Modelo aprimorado de Levins para 2 espécies: evolução do sistema no espaçode estados
# Jhordan Silveira de Borba
# sbjhordan@gmail.com

def phase2():

    #Parâmetros    
    c1=0.1                   # Fator de colonização do guanaco 
    cy=0.015                 # Fator de colonização do puma
    e1=0.025                 # Fator de extinção local do guanaco
    ey=0.015                 # Fator de extinção local do puma
    u1=0.3                   # Fator de predação do guanaco
    N=int(200000)            # Duração da simulação
    d=0.01                   # Tamanho do passo
    D=0.5                    # Destruição do habitat
    
    p1=[0.,0.]      # Ponto de equilíbrio 1
    p2=[0.65,0.]    # Ponto de equilíbrio 2
    p3=[-3.26,1.30] # Ponto de equilíbrio 3
    p4=[0.92,-0.09] # Ponto de equilíbrio 4
    
    #Valores iniciais:
    init=[(0.4,0.4),(0.3,0.3),(0.05,0.05)]
    c=0
    for it in init:
        x=[]
        y=[]
        x.append(it[0])
        y.append(it[1])
        for i in range(N-1):
            x.append(x[i]+d*(c1*x[i]*(1-D-x[i])-e1*x[i]-u1*x[i]*y[i]))
            y.append(y[i]+d*(cy*y[i]*(x[i]-y[i]*(x[i]))-ey*y[i]))
        if(c==0):
            plt.plot(x,y,'g-')
            plt.plot(it[0],it[1],'go')
            D=0.7
        elif (c==1):
            plt.plot(x,y,'b-')
            plt.plot(it[0],it[1],'bo')
            D=0.95
        else:
            plt.plot(x,y,'r-')
            plt.plot(it[0],it[1],'ro')
        c=c+1
        
    plt.plot(p1[0],p1[1],'ko')
    plt.plot(p2[0],p2[1],'ko')
    plt.plot(p3[0],p3[1],'ko')
    plt.plot(p4[0],p4[1],'ko')
    plt.xlim(0,0.5)
    plt.ylim(0,0.5)
    plt.show()

Principal material utilizado

1. Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances (Fabiana Laguna e outros, Ecological Modelling)

Anterior: Modelo de Lotka-Volterra amortecido | Índice: Ecologia | Próximo: Modelo espacialmente explícito