Métodos Computacionais para Estudo de Fenômenos Ondulatórios: mudanças entre as edições
| (81 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 2: | Linha 2: | ||
Este trabalho tem como objetivo realizar um estudo introdutório da equação da onda, adotando uma abordagem computacional que proporciona uma base teórica sólida e intuitiva. Inicialmente, é realizada a implementação de uma solução numérica (FTCS) para a equação da advecção, visando o estudo da propagação de uma perturbação e explorando aspectos computacionais fundamentais. Em seguida, a equação da onda é aplicada em uma dimensão, permitindo uma investigação detalhada de fenômenos ondulatórios, tais como reflexão, interferência e refração. A abordagem é estendida para duas dimensões, incluindo a análise dos efeitos de contorno nesse contexto. Por fim, o trabalho aprofunda-se no estudo do fenômeno de difração, contribuindo para uma compreensão mais enriquecedora dos aspectos complexos dos fenômenos ondulatórios em múltiplas dimensões. | Este trabalho tem como objetivo realizar um estudo introdutório da equação da onda, adotando uma abordagem computacional que proporciona uma base teórica sólida e intuitiva. Inicialmente, é realizada a implementação de uma solução numérica (FTCS) para a equação da advecção, visando o estudo da propagação de uma perturbação e explorando aspectos computacionais fundamentais. Em seguida, a equação da onda é aplicada em uma dimensão, permitindo uma investigação detalhada de fenômenos ondulatórios, tais como reflexão, interferência e refração. A abordagem é estendida para duas dimensões, incluindo a análise dos efeitos de contorno nesse contexto. Por fim, o trabalho aprofunda-se no estudo do fenômeno de difração, contribuindo para uma compreensão mais enriquecedora dos aspectos complexos dos fenômenos ondulatórios em múltiplas dimensões. | ||
= Introdução = | = Introdução = | ||
| Linha 10: | Linha 11: | ||
Com base no exposto, propõe-se a realização de um estudo abrangente sobre a modelagem de fenômenos ondulatórios. Inicialmente, serão apresentados pontos importantes acerca da equação da onda. Em seguida, dedicaremos atenção ao estudo da propagação de uma perturbação a partir da equação de advecção. Nesse contexto, abriremos a discussão sobre a abordagem computacional, e, tangencialmente, comentaremos sobre outros métodos numéricos para resolver a advecção. Posteriormente, faremos um estudo sobre a solução numérica da equação da onda, permitindo a modelagem de fenômenos ondulatórios, como reflexão, interferência, refração e difração. | Com base no exposto, propõe-se a realização de um estudo abrangente sobre a modelagem de fenômenos ondulatórios. Inicialmente, serão apresentados pontos importantes acerca da equação da onda. Em seguida, dedicaremos atenção ao estudo da propagação de uma perturbação a partir da equação de advecção. Nesse contexto, abriremos a discussão sobre a abordagem computacional, e, tangencialmente, comentaremos sobre outros métodos numéricos para resolver a advecção. Posteriormente, faremos um estudo sobre a solução numérica da equação da onda, permitindo a modelagem de fenômenos ondulatórios, como reflexão, interferência, refração e difração. | ||
= Equação da Onda = | = Equação da Onda = | ||
A função de uma onda é aquela que especifica o valor da perturbação em cada ponto e instante ao longo de seu percurso. Para iniciar nossa análise, abordaremos o exemplo mais simples, em que a propagação ocorre unicamente em uma direção, como é o caso das ondas transversais em uma corda. | A função de uma onda é aquela que especifica o valor da perturbação em cada ponto e instante ao longo de seu percurso. Para iniciar nossa análise, abordaremos o exemplo mais simples, em que a propagação ocorre unicamente em uma direção, como é o caso das ondas transversais em uma corda. | ||
== Dedução == | == Dedução == | ||
O perfil da onda em uma corda em um determinado instante é equivalente à forma que a corda apresenta nesse momento, que é dada pela função <math>y(x, t)</math>. A perturbação assume a forma de uma onda progressiva, movendo-se como uma entidade coesa para a direita, mantendo sua configuração inalterada, com velocidade <math>v</math>. Dessa forma, ao acompanhar a onda em um referencial inercial diferente, em que <math>y(x,t)=y(x',t)</math>, onde <math>x'</math> representa o antigo <math>x</math> deslocado por <math>vt</math>, a relação entre os dois referenciais é estabelecida por | O perfil da onda em uma corda em um determinado instante é equivalente à forma que a corda apresenta nesse momento, que é dada pela função <math>y(x, t)</math>. A perturbação assume a forma de uma onda progressiva, movendo-se como uma entidade coesa para a direita, mantendo sua configuração inalterada, com velocidade <math>v</math>. Dessa forma, ao acompanhar a onda em um referencial inercial diferente, em que <math>y(x,t)=y(x',t)</math>, onde <math>x'</math> representa o antigo <math>x</math> deslocado por <math>vt</math>, a relação entre os dois referenciais é estabelecida por | ||
<center><math> | <center><math> | ||
| Linha 108: | Linha 108: | ||
</math></center> | </math></center> | ||
Dessa forma, torna-se evidente que a razão entre as funções de < | Dessa forma, torna-se evidente que a razão entre as funções de <math>T</math> consiste em uma constante, assim como <math>v^2 \frac{X''}{X}</math>. | ||
<center><math> | <center><math> | ||
v^2 \frac{X''}{X} = \lambda ^2 \to X'' = \bigg(\frac{\lambda}{v}\bigg)^2 X | v^2 \frac{X''}{X} = \lambda ^2 \to X'' = \bigg(\frac{\lambda}{v}\bigg)^2 X | ||
</math></center> | </math></center> '''(I)''' | ||
<center><math> | <center><math> | ||
\frac{T''}{T} = \lambda ^2 \to T''= \lambda^2 T | \frac{T''}{T} = \lambda ^2 \to T''= \lambda^2 T | ||
</math></center> | </math></center> '''(II)''' | ||
Observa-se que as equações ( | Observa-se que as equações (I) e (II) são equações diferenciais ordinárias (EDOs) lineares de segunda ordem, cujos coeficientes podem depender da variável independente e, potencialmente, serem funções não constantes. Assim, é possível usarmos das condições de contorno para resolver essas equações. | ||
'''Resolvendo a Equação ( | '''Resolvendo a Equação (I)''' | ||
Se avaliarmos as condições de contorno para os possíveis valores de lambda, que devem ser maiores ou iguais a zero, obtemos apenas a solução trivial. Contudo, se lambda for negativo, surge uma solução para <math>X(x)</math> na forma | Se avaliarmos as condições de contorno para os possíveis valores de lambda, que devem ser maiores ou iguais a zero, obtemos apenas a solução trivial. Contudo, se lambda for negativo, surge uma solução para <math>X(x)</math> na forma | ||
| Linha 148: | Linha 144: | ||
</math></center> | </math></center> | ||
'''Resolvendo a Equação (II)''' | |||
Analogamente, temos uma solução não trivial para lambda menor que zero. | Analogamente, temos uma solução não trivial para lambda menor que zero. | ||
| Linha 193: | Linha 189: | ||
B_n = \frac{2}{nv \pi}\int_0^L g(x) \sin \bigg( \frac{n\pi x}{L} \bigg) dx | B_n = \frac{2}{nv \pi}\int_0^L g(x) \sin \bigg( \frac{n\pi x}{L} \bigg) dx | ||
</math></center> | </math></center> | ||
=== Implementação da Solução Analítica === | |||
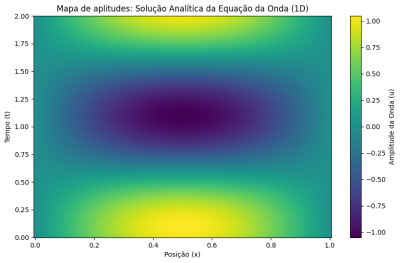
[[Arquivo:eq onda analitica.png|thumb|upright=0.0|right|400px]] | |||
Se considerarmos 10 como o número máximo de termos na série de Fourier de uma corda com comprimento <math>L=1</math> e velocidade <math>v=1</math>, é possível criar um mapa da amplitude em função das posições de cada ponto da corda e do tempo. Esse tipo de gráfico será recorrente em nossa análise em diferentes casos. | |||
Neste caso, é possível observar que inicialmente a corda possui um máximo localizado no centro do eixo de posição, com mínimos iguais a zero nas extremidades do eixo. À medida que a função evolui no tempo, a amplitude diminui, passando por um instante onde em todos os pontos da corda a amplitude é zero, e prossegue para completar um meio período, onde apresenta um mínimo menor que zero centrado no eixo x e máximos iguais a zero nas extremidades da corda. | |||
= A equação de advecção unidimensional = | = A equação de advecção unidimensional = | ||
| Linha 202: | Linha 205: | ||
<center><math> | <center><math> | ||
\frac{\partial u}{\partial t} + v\frac{\partial u}{\partial x} = 0 | \frac{\partial u}{\partial t} + v\frac{\partial u}{\partial x} = 0 | ||
</math></center> | </math></center> | ||
A equação a seguir descreve a advecção passiva de um campo escalar <math>u(x,t)</math> transportado por um fluxo de velocidade constante <math>v</math>. Como a equação de advecção é um tanto mais simples do que a equação da onda, discutiremos aquela em primeiro lugar. A equação de advecção possui a solução formal: | A equação a seguir descreve a advecção passiva de um campo escalar <math>u(x,t)</math> transportado por um fluxo de velocidade constante <math>v</math>. Como a equação de advecção é um tanto mais simples do que a equação da onda, discutiremos aquela em primeiro lugar. A equação de advecção possui a solução formal: | ||
| Linha 208: | Linha 211: | ||
<center><math> | <center><math> | ||
u(x,t) = F(x-vt) | u(x,t) = F(x-vt) | ||
</math></center> | </math></center> | ||
Essa solução descreve um pulso de forma arbitrária que é arrastado pelo fluxo a uma velocidade constante <math>v</math>, sem alterar sua forma. | Essa solução descreve um pulso de forma arbitrária que é arrastado pelo fluxo a uma velocidade constante <math>v</math>, sem alterar sua forma. | ||
== | == Esquema FTCS para equação da advecção == | ||
Para a abordagem numérica computacional do nosso estudo, utilizamos o esquema FTCS (Forward Time-Centered Space). | |||
Para a abordagem numérica computacional do nosso estudo, utilizamos o esquema FTCS. | |||
O método FTCS é amplamente empregado na resolução de equações diferenciais parciais. Trata-se de um método de diferenças finitas que adota uma abordagem explícita no tempo e central no espaço. Esse esquema apresenta uma acurácia de primeira ordem no tempo e de segunda ordem no espaço. | O método FTCS é amplamente empregado na resolução de equações diferenciais parciais. Trata-se de um método de diferenças finitas que adota uma abordagem explícita no tempo e central no espaço. Esse esquema apresenta uma acurácia de primeira ordem no tempo e de segunda ordem no espaço. | ||
| Linha 224: | Linha 225: | ||
<center><math> | <center><math> | ||
\frac{\partial u}{\partial t} \approx \frac{u_i^{n+1} - u_i^n}{\Delta t} | \frac{\partial u}{\partial t} \approx \frac{u_i^{n+1} - u_i^n}{\Delta t} | ||
</math></center> | </math></center> | ||
onde <math>u_i^n</math> representa a amplitude da perturbação no ponto <math>i</math> do espaço e no instante <math>n</math>, e <math>\Delta t</math> é o passo de tempo. | onde <math>u_i^n</math> representa a amplitude da perturbação no ponto <math>i</math> do espaço e no instante <math>n</math>, e <math>\Delta t</math> é o passo de tempo. | ||
| Linha 232: | Linha 233: | ||
<center><math> | <center><math> | ||
\frac{\partial u}{\partial x} \approx \frac{u_{i+1}^n - u_{i-1}^n}{2\Delta x} | \frac{\partial u}{\partial x} \approx \frac{u_{i+1}^n - u_{i-1}^n}{2\Delta x} | ||
</math></center> | </math></center> | ||
onde <math>\Delta x</math> é o espaçamento entre os pontos discretizados no espaço. | onde <math>\Delta x</math> é o espaçamento entre os pontos discretizados no espaço. | ||
| Linha 240: | Linha 241: | ||
<center><math> | <center><math> | ||
u_i^{n+1}= u_i^n + \frac{r}{2} (u_{i+1}^n - u_{i-1}^n) | u_i^{n+1}= u_i^n + \frac{r}{2} (u_{i+1}^n - u_{i-1}^n) | ||
</math></center> | </math></center> | ||
onde <math>r = v\frac{\Delta t}{\Delta x}</math>. | onde <math>r = v\frac{\Delta t}{\Delta x}</math>. | ||
| Linha 250: | Linha 251: | ||
<center><math> | <center><math> | ||
u(x, t) = A(t)e^{jkx} | u(x, t) = A(t)e^{jkx} | ||
</math></center> | </math></center> | ||
onde <math>j = \sqrt{-1}</math>, <math>k</math> é o número de onda, e <math>A</math> é a amplitude da onda, uma função do tempo. | onde <math>j = \sqrt{-1}</math>, <math>k</math> é o número de onda, e <math>A</math> é a amplitude da onda, uma função do tempo. | ||
| Linha 258: | Linha 259: | ||
<center><math> | <center><math> | ||
A_ne^{jki\Delta x} | A_ne^{jki\Delta x} | ||
</math></center> | </math></center> | ||
Substituindo esta solução tentativa na expressão da advecção discretizada temos: | Substituindo esta solução tentativa na expressão da advecção discretizada temos: | ||
| Linha 264: | Linha 265: | ||
<center><math> | <center><math> | ||
A_{n+1}e^{jki\Delta x} = A_ne^{jki\Delta x} - \frac{u\Delta t}{2\Delta x}\left(A_ne^{jk(i+1)\Delta x} - A_ne^{jk(i-1)\Delta x}\right) | A_{n+1}e^{jki\Delta x} = A_ne^{jki\Delta x} - \frac{u\Delta t}{2\Delta x}\left(A_ne^{jk(i+1)\Delta x} - A_ne^{jk(i-1)\Delta x}\right) | ||
</math></center>( | </math></center>(III) | ||
Seja <math>\xi</math> a razão da amplitude da onda no passo de tempo <math>n + 1</math> em relação ao passo <math>n</math>. Portanto, | Seja <math>\xi</math> a razão da amplitude da onda no passo de tempo <math>n + 1</math> em relação ao passo <math>n</math>. Portanto, | ||
| Linha 270: | Linha 271: | ||
<center><math> | <center><math> | ||
\xi = \frac{A_{n+1}}{A_n} | \xi = \frac{A_{n+1}}{A_n} | ||
</math></center> | </math></center> | ||
Dividir ( | Dividir (III) por <math>A_n</math> resulta em | ||
<center><math> | <center><math> | ||
\xi e^{jki\Delta x} = e^{jki\Delta x} - \frac{u\Delta t}{2\Delta x}\left(e^{jk(i+1)\Delta x} - e^{jk(i-1)\Delta x}\right) | \xi e^{jki\Delta x} = e^{jki\Delta x} - \frac{u\Delta t}{2\Delta x}\left(e^{jk(i+1)\Delta x} - e^{jk(i-1)\Delta x}\right) | ||
</math></center> | </math></center> | ||
Se dividirmos esse resultado por <math>e^{jki\Delta x}</math> temos: | Se dividirmos esse resultado por <math>e^{jki\Delta x}</math> temos: | ||
| Linha 282: | Linha 283: | ||
<center><math> | <center><math> | ||
\xi = 1 - \frac{u\Delta t}{2\Delta x}\left(e^{jk\Delta x} - e^{-jk\Delta x}\right) = 1 - \frac{u\Delta t}{\Delta xj}\sin(k\Delta x) | \xi = 1 - \frac{u\Delta t}{2\Delta x}\left(e^{jk\Delta x} - e^{-jk\Delta x}\right) = 1 - \frac{u\Delta t}{\Delta xj}\sin(k\Delta x) | ||
</math></center> | </math></center> | ||
Assim, | Assim, | ||
| Linha 288: | Linha 289: | ||
<center><math> | <center><math> | ||
|\xi| = \sqrt{1 + \left(\frac{u\Delta t}{\Delta x}\sin(k\Delta x)\right)^2} | |\xi| = \sqrt{1 + \left(\frac{u\Delta t}{\Delta x}\sin(k\Delta x)\right)^2} | ||
</math></center> | </math></center> | ||
Isso implica que <math>|\xi| \geq 1</math> independentemente do passo de tempo <math>\Delta t</math> selecionado ou do passo espacial <math>\Delta x</math>, portanto, FTCS é incondicionalmente instável. | Isso implica que <math>|\xi| \geq 1</math> independentemente do passo de tempo <math>\Delta t</math> selecionado ou do passo espacial <math>\Delta x</math>, portanto, FTCS é incondicionalmente instável. | ||
| Linha 299: | Linha 300: | ||
== Implementação do esquema FTCS == | == Implementação do esquema FTCS == | ||
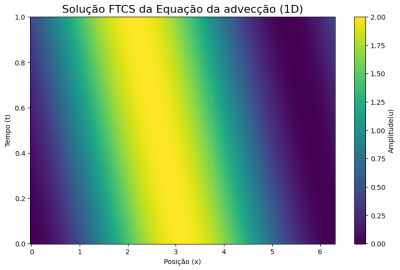
[[Arquivo:ftcs eq advec.png|thumb|upright=0.0|right|400px]] | |||
Vamos agora examinar a implementação do esquema FTCS na equação da advecção para visualizarmos a propagação de uma perturbação na forma de <math>1-\cos(x)</math> em um eixo <math>x</math> infinito. Em outras palavras: | Vamos agora examinar a implementação do esquema FTCS na equação da advecção para visualizarmos a propagação de uma perturbação na forma de <math>1-\cos(x)</math> em um eixo <math>x</math> infinito. Em outras palavras: | ||
| Linha 305: | Linha 308: | ||
* Condições de contorno periódicas. | * Condições de contorno periódicas. | ||
Neste caso, podemos observar uma perturbação se propagando no sentido negativo do eixo <math>x</math> sem perda de amplitude ou mudança de forma. Isso acontece porque, com a equação da advecção, podemos analisar apenas a cinemática de uma perturbação, a qual, por sua vez, apenas relaciona os atributos como amplitude, comprimento de onda, frequência e velocidade. | Neste caso, podemos observar uma perturbação se propagando no sentido negativo do eixo <math>x</math> sem perda de amplitude ou mudança de forma. Isso acontece porque, com a equação da advecção, podemos analisar apenas a cinemática de uma perturbação, a qual, por sua vez, apenas relaciona os atributos como amplitude, comprimento de onda, frequência e velocidade. | ||
| Linha 320: | Linha 319: | ||
<center><math> | <center><math> | ||
\frac{\partial^2 u}{\partial t^2} = v^2 \frac{\partial^2 u}{\partial x^2} | \frac{\partial^2 u}{\partial t^2} = v^2 \frac{\partial^2 u}{\partial x^2} | ||
</math></center> | </math></center> | ||
onde <math>u</math> geralmente é algum tipo de deslocamento ou perturbação, enquanto <math>v</math> é a velocidade da onda. A equação de onda possui a solução formal | onde <math>u</math> geralmente é algum tipo de deslocamento ou perturbação, enquanto <math>v</math> é a velocidade da onda. A equação de onda possui a solução formal | ||
| Linha 326: | Linha 325: | ||
<center><math> | <center><math> | ||
u(x,t) = F(x+vt) + G(x+vt), | u(x,t) = F(x+vt) + G(x+vt), | ||
</math></center> | </math></center> | ||
onde <math>F</math> e <math>G</math> são funções arbitrárias. A solução acima representa pulsos de onda de formato arbitrário que se propagam com velocidade <math>v</math> nas direções <math>+x</math> e <math>-x</math>, respectivamente, sem alterar a forma. | onde <math>F</math> e <math>G</math> são funções arbitrárias. A solução acima representa pulsos de onda de formato arbitrário que se propagam com velocidade <math>v</math> nas direções <math>+x</math> e <math>-x</math>, respectivamente, sem alterar a forma. | ||
== Esquema FTCS == | == Esquema FTCS para equação da onda unidimensional== | ||
Iniciamos o estudo da solução numérica da equação da onda a partir da implementação do esquema FTCS, pois, como comentado antes, este é o método de implementação mais prático para generalizarmos para mais dimensões espaciais. | Iniciamos o estudo da solução numérica da equação da onda a partir da implementação do esquema FTCS, pois, como comentado antes, este é o método de implementação mais prático para generalizarmos para mais dimensões espaciais. | ||
| Linha 338: | Linha 337: | ||
<center><math> | <center><math> | ||
\frac{\partial^2}{\partial t^2}u(x_i,t_n)\approx \frac{u_i^{n+1} - 2u_i^n + u_i^{n-1}}{\Delta t^2} | \frac{\partial^2}{\partial t^2}u(x_i,t_n)\approx \frac{u_i^{n+1} - 2u_i^n + u_i^{n-1}}{\Delta t^2} | ||
</math></center> | </math></center> | ||
Uma aproximação semelhante para a derivada de segunda ordem na direção <math>x</math> é dada por | Uma aproximação semelhante para a derivada de segunda ordem na direção <math>x</math> é dada por | ||
| Linha 344: | Linha 343: | ||
<center><math> | <center><math> | ||
\frac{\partial^2}{\partial x^2}u(x_i,t_n)\approx \frac{u_{i+1}^{n} - 2u_i^n + u_{i-1}^{n}}{\Delta x^2} | \frac{\partial^2}{\partial x^2}u(x_i,t_n)\approx \frac{u_{i+1}^{n} - 2u_i^n + u_{i-1}^{n}}{\Delta x^2} | ||
</math></center> | </math></center> | ||
Agora podemos substituir as derivadas e obter | Agora podemos substituir as derivadas e obter | ||
| Linha 350: | Linha 349: | ||
<center><math> | <center><math> | ||
\frac{u_i^{n+1} - 2u_i^n + u_i^{n-1}}{\Delta t^2} = v^2\frac{u_{i+1}^{n} - 2u_i^n + u_{i-1}^{n}}{\Delta x^2}. | \frac{u_i^{n+1} - 2u_i^n + u_i^{n-1}}{\Delta t^2} = v^2\frac{u_{i+1}^{n} - 2u_i^n + u_{i-1}^{n}}{\Delta x^2}. | ||
</math></center> | </math></center> | ||
Assumimos que <math>u^n_i</math> e <math>u^{n-1}_i</math> já foram calculados para <math>i=0,\ldots,N_x</math>. A única quantidade desconhecida é, portanto, <math>u^{n+1}_i</math>, que podemos resolver da seguinte forma: | Assumimos que <math>u^n_i</math> e <math>u^{n-1}_i</math> já foram calculados para <math>i=0,\ldots,N_x</math>. A única quantidade desconhecida é, portanto, <math>u^{n+1}_i</math>, que podemos resolver da seguinte forma: | ||
| Linha 356: | Linha 355: | ||
<center><math> | <center><math> | ||
u^{n+1}_i = -u^{n-1}_i + 2u^n_i + r^2 \left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right), | u^{n+1}_i = -u^{n-1}_i + 2u^n_i + r^2 \left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right), | ||
</math></center> | </math></center> | ||
onde introduzimos o parâmetro | onde introduzimos o parâmetro | ||
| Linha 367: | Linha 366: | ||
== Análise de estabilidade de von Neumann == | == Análise de estabilidade de von Neumann == | ||
Pela análise de Von Neumann, substituímos <math>u_n</math> por <math>g_n e^{i\theta}</math> na equação da onda. Após manipulações, a expressão resultante é: | Pela análise de Von Neumann, substituímos <math>u_n</math> por <math>g_n e^{i\theta}</math> na equação da onda. Após manipulações, a expressão resultante é: | ||
| Linha 374: | Linha 371: | ||
<center><math> | <center><math> | ||
g = 2 - g^{-1} + \frac{C}{2}(e^{i\theta} - 2 + e^{-i\theta}) | g = 2 - g^{-1} + \frac{C}{2}(e^{i\theta} - 2 + e^{-i\theta}) | ||
</math></center> | </math></center> | ||
Usando a identidade de Euler <math>e^{i\theta} + e^{-i\theta} = 2 \cos \theta</math>, chegamos a: | Usando a identidade de Euler <math>e^{i\theta} + e^{-i\theta} = 2 \cos \theta</math>, chegamos a: | ||
| Linha 380: | Linha 377: | ||
<center><math> | <center><math> | ||
g^2 - 2[1 - \frac{C}{2}(1 - \cos \theta)]g + 1 = 0 | g^2 - 2[1 - \frac{C}{2}(1 - \cos \theta)]g + 1 = 0 | ||
</math></center> | </math></center> | ||
Reescrevendo <math>\cos \theta = \cos^2\left(\frac{\theta}{2}\right) - \sin^2\left(\frac{\theta}{2}\right)</math>, a equação torna-se: | Reescrevendo <math>\cos \theta = \cos^2\left(\frac{\theta}{2}\right) - \sin^2\left(\frac{\theta}{2}\right)</math>, a equação torna-se: | ||
| Linha 386: | Linha 383: | ||
<center><math> | <center><math> | ||
g^2 + 2(2C^2 \sin^2\left(\frac{\theta}{2}\right) - 1)g + 1 = 0 | g^2 + 2(2C^2 \sin^2\left(\frac{\theta}{2}\right) - 1)g + 1 = 0 | ||
</math></center> | </math></center> | ||
Expressamos isso como <math>g^2 + 2bg + 1 = 0</math>, onde <math>b = 2C^2 \sin^2\left(\frac{\theta}{2}\right) - 1</math>. As raízes são: | Expressamos isso como <math>g^2 + 2bg + 1 = 0</math>, onde <math>b = 2C^2 \sin^2\left(\frac{\theta}{2}\right) - 1</math>. As raízes são: | ||
| Linha 392: | Linha 389: | ||
<center><math> | <center><math> | ||
g = \begin{cases} -b \pm \sqrt{b^2 - 1}, & \text{se } |b| > 1 \\ -b \pm i\sqrt{1 - b^2}, & \text{se } |b| \leq 1 \end{cases} | g = \begin{cases} -b \pm \sqrt{b^2 - 1}, & \text{se } |b| > 1 \\ -b \pm i\sqrt{1 - b^2}, & \text{se } |b| \leq 1 \end{cases} | ||
</math></center> | </math></center> | ||
Se <math>|b| > 1</math>, implica <math>C \leq 1</math>. Se <math>|b| \leq 1</math>, <math>C \leq 1</math> pela condição de Von Neumann, tornando o método condicionalmente estável pela condição CFL. | Se <math>|b| > 1</math>, implica <math>C \leq 1</math>. Se <math>|b| \leq 1</math>, <math>C \leq 1</math> pela condição de Von Neumann, tornando o método condicionalmente estável pela condição CFL. | ||
| Linha 405: | Linha 402: | ||
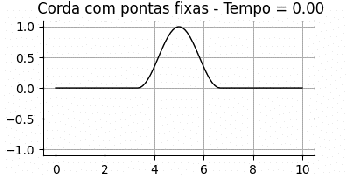
=== Perturbação em uma corda com extremidades fixas === | === Perturbação em uma corda com extremidades fixas === | ||
Neste caso, é possível observar que a corda iniciará a partir do seu ponto mais alto no centro do eixo. A perturbação se propagará igualmente para ambos os sentidos do eixo. Ao atingir as extremidades fixas, as duas perturbações, invertidas, deslocam-se em direção ao centro da corda, onde interferem de forma construtiva e produzem um mínimo de amplitude. | |||
<center> | |||
{| | |||
|[[Arquivo:corda_ponta_fixa.gif|thumb|upright=0.0|center|Evolução temporal da amplitude pela posição no eixo x em uma corda com extremidades fixas|350px]] | |||
|[[Arquivo:MA corda com pontas fixas.png|thumb|upright=0.0|center|310px]] | |||
|} | |||
</center> | |||
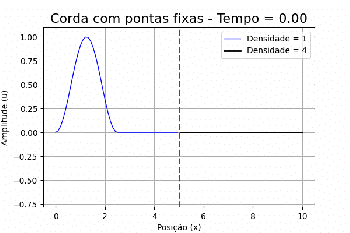
=== Perturbação em uma corda com extremidades móveis === | === Perturbação em uma corda com extremidades móveis === | ||
Com extremidades móveis, não se observa uma mudança de fase da perturbação inicial ao atingir os extremos da corda. No entanto, ao implementarmos condições de contorno periódicas, implicamos que, ao alcançar uma das extremidades da corda, o pulso retorna à outra extremidade, continuando a se propagar na mesma direção e com a mesma velocidade. Como a perturbação inicial gera dois pulsos se propagando em direções opostas a partir do centro do eixo, com velocidades iguais, percebemos a interação construtiva dos pulsos que alcançam os limites do eixo simultaneamente. Isso faz com que retornem a se propagar em direção ao centro, gerando máximos de amplitude em cada interação. | |||
<center> | |||
{| | |||
|[[Arquivo:corda_ponta_solta.gif|thumb|upright=0.0|center|Evolução temporal da amplitude pela posição no eixo x em uma corda com extremidades interligadas por condições de contorno periódicas.|350px]] | |||
|[[Arquivo:MA corda com pontas soltas.png|thumb|upright=0.0|center|310px]] | |||
|} | |||
</center> | |||
=== Alteração no meio de propagação === | === Alteração no meio de propagação === | ||
A refração é um fenômeno que ocorre quando uma onda passa de um meio para outro com uma velocidade de propagação diferente. Esse fenômeno é mais comumente associado a ondas de luz, mas também pode ocorrer com ondas sonoras, ondas de rádio, ondas sísmicas e outras formas de ondas. | |||
Se uma onda se propaga em uma corda e encontra uma mudança abrupta nas propriedades da corda, como a densidade ou a tensão, isso pode resultar em uma mudança na velocidade da onda. O grau de refração dependerá das diferenças nas propriedades do meio antes e depois da mudança. | |||
<center> | |||
{| | |||
|[[Arquivo:muda_meio_de_propag.gif|thumb|upright=0.0|center|Evolução temporal da amplitude pela posição no eixo x em uma corda com extremidades fixas e diferentes densidades.|350px]] | |||
|[[Arquivo:MA corda muda meio.png|thumb|upright=0.0|center|340px]] | |||
|} | |||
</center> | |||
Em um modelo que considera a reflexão e a refração na junção das duas ondas [Elmore e Head], é demonstrado que a razão entre as amplitudes da onda refratada (<math>A_2</math>) e a amplitude da onda incidente (<math>A_1</math>) é dada por: | |||
<center><math> | |||
\frac{A_2}{A_1} = \frac{2\sqrt{\mu_1}}{\sqrt{\mu_1} +\sqrt{\mu_2}} | |||
</math></center> | |||
Usando a relação da velocidade de propagação com as variáveis de tensão e densidade podemos chegar em expressões para as amplitudes do pulso que irá voltar (<math>A_v</math>) e do pulso que irá passar para a outra corda (<math>A_p</math>). | |||
<center><math> | |||
A_p = \frac{2v_2}{v_1 + v_2}A_i | |||
</math></center> | |||
<center><math> | |||
A_v = \frac{|v_1 - v_2|}{v_1 + v_2}A_i | |||
</math></center> | |||
'''(IV)''' | |||
onde <math>A_i</math> é a amplitude do pulso incidente. | |||
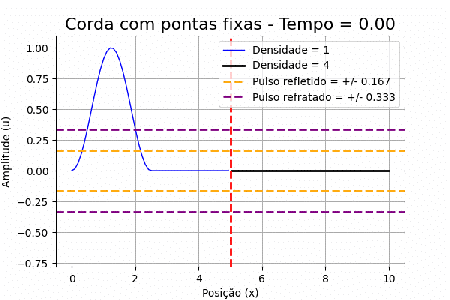
No nosso caso, a perturbação inicial tem amplitude de 1, porém propaga-se isotopicamente nos dois sentidos do eixo x. O pulso que se desloca no sentido negativo do eixo interage imediatamente com o ponto fixo da corda e torna a propagar-se no sentido positivo, mas agora com uma fase. Assim, temos dois pulsos, um positivo e um negativo, ambos com amplitude igual a <math>0.5</math>, propagando-se em direção a outra corda de densidade diferente. | |||
Com as velocidades de propagação nos dois meios, utilizando as fórmulas em (IV), podemos determinar que a amplitude do pulso que irá voltar é <math>0,167</math>, enquanto a do pulso que será refratado é <math>0,333</math>. | |||
[[Arquivo:muda_meio_de_propag_analise.gif|thumb|upright=0.0|center|450px]] | |||
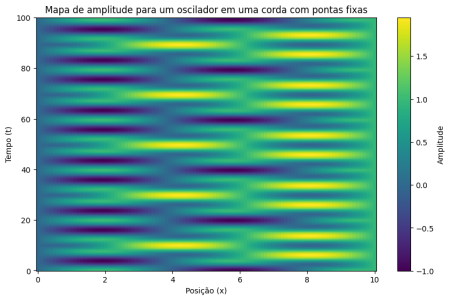
=== Oscilador em uma corda === | === Oscilador em uma corda === | ||
Agora, em vez de variarmos as condições de contorno para um pulso senoidal em uma corda, estamos avaliando um oscilador senoidal acoplado a corda com parâmetros físicos bem definidos: amplitude (A), frequência (f) e comprimento de onda ( λ ). Assim, ao invés de termos uma condição inicial que aplicada em um pequena porção da corda se propaga, iremos avaliar um oscilador da forma <math>A\sin(kx)</math> que define a amplitude inicial para cada ponto da corda, onde <math>k</math> é o número de onda definido como duas vezes <math>\pi</math> sobre o comprimento de onda. Vale notar ainda que λ é uma função da velocidade de propagação (propriedade da corda) e da frequência (propriedade do oscilado). | |||
Seja <math>A = 1</math>, <math>v = 1</math> e <math>f = 0.13</math>, que resulta em um comprimento de onda igual a 7.7. Implementando um oscilador com esses parâmetros para uma corda com extremidades fixas, obtemos | |||
[[Arquivo:oscilador com pontas fixas.png|thumb|upright=0.0|center|450px]] | |||
Observamos que, ao ajustar arbitrariamente os parâmetros do oscilador, obtemos regiões mais escuras e mais claras, pouco organizadas. Nessas regiões, ocorrem interferências destrutivas e construtivas, respectivamente. As interferências ocorrem de forma pouco definida, uma vez que não há, nesse caso, um padrão bem definido para as interações que a onda sofrerá. No entanto, veremos que isso pode ser modificado. | |||
=== Ondas estacionárias === | === Ondas estacionárias === | ||
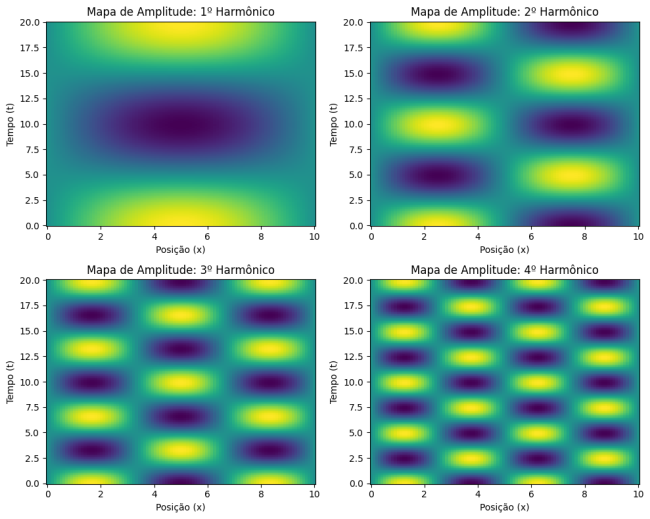
= A | A relação entre o comprimento de onda da onda incidente ( λ) e a distância disponível para a onda se refletir (<math>2L</math>, onde <math>L</math> é o comprimento da região confinada, da corda) deve permitir a formação de nós e ventres estacionários. Para ondas estacionárias em uma corda com extremidades fixas, os comprimentos de onda permitidos são dados por <math>\lambda_n = \frac{2L}{n}</math>, onde <math>n</math> é um número inteiro positivo. | ||
Essa fórmula mostra que à medida que <math>n</math> aumenta, o comprimento de onda diminui. Cada valor de <math>n</math> corresponde a uma harmônica específica, que representa o número de meios comprimentos de onda que cabem na corda. A primeira harmônica (<math>n = 1</math>) tem um nó em cada extremidade da corda, a segunda harmônica (<math>n = 2</math>) tem dois nós, e assim por diante. | |||
Dado que <math>\lambda = \frac{v}{f} </math> e <math>\lambda_n = \frac{2L}{n}</math>, é possível expressar um conjunto discreto de frequências para o nosso oscilador, as quais resultam em ondas estacionárias. | |||
<center><math> | |||
f_n = \frac{nv}{2L} | |||
</math></center> | |||
Dessa forma, podemos aplicar valores de <math>f</math> condicionados a gerar as condições necessárias para a formação de ondas estacionárias. | |||
[[Arquivo:ondas_estacionarias.png|thumb|upright=0.0|center|650px]] | |||
= A Equação da Onda em Duas Dimensões = | |||
Agora, procederemos à avaliação da modelagem de ondas em duas dimensões. Nesse contexto, além dos fenômenos já observados, é possível perceber também a difração. | |||
== FTCS == | == Esquema FTCS para Equação da Onda Bidimensional== | ||
Em duas dimensões, a equação da onda é dada por | |||
<center><math> | <center><math> | ||
\frac{\partial^2 | \frac{\partial^2 f}{\partial t^2} = v^2 \left( \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} \right). | ||
</math></center> | </math></center> | ||
Aproximando todas as derivadas parciais por uma diferença finita centrada, segue que | |||
<center><math> | <center><math> | ||
\frac{\partial^2 | \frac{\partial^2 f}{\partial t^2} \approx \frac{f^{n+1}_{i,j} - 2f^{n}_{i,j} + f^{n-1}_{i,j}}{\Delta t^2},\qquad | ||
\frac{\partial^2 f}{\partial x^2} \approx \frac{f^{n}_{i+1,j} - 2f^{n}_{i,j} + f^{n}_{i-1,j}}{\Delta x^2},\qquad | |||
\frac{\partial^2 f}{\partial y^2} \approx \frac{f^{n}_{i,j+1} - 2f^{n}_{i,j} + f^{n}_{i,j-1}}{\Delta y^2}. | |||
</math></center> | </math></center> | ||
Portanto, em forma discreta, a equação da onda pode ser escrita como | |||
<center><math> | <center><math> | ||
\frac{\ | f^{n+1}_{i,j} = 2f^{n}_{i,j} - f^{n-1}_{i,j} + v^2 \left[ \frac{\Delta t^2}{\Delta x^2} \left(f^{n}_{i+1,j} - 2f^{n}_{i,j} + f^{n}_{i-1,j}\right) + \frac{\Delta t^2}{\Delta y^2} \left(f^{n}_{i,j+1} - 2f^{n}_{i,j} + f^{n}_{i,j-1}\right) \right]. | ||
</math></center> | </math></center> | ||
Para <math>\Delta x = \Delta y</math>, segue que | |||
<center><math> | <center><math> | ||
f^{n+1}_{i,j} = \left(2-4a\right)f^{n}_{i,j} - f^{n-1}_{i,j} + a\left(f^n_{i-1,j}+f^n_{i+1,j}+f^n_{i,j-1}+f^n_{i,j+1}\right), \qquad a\equiv \left(v\frac{\Delta t}{\Delta x}\right)^2 | |||
</math></center> | </math></center> | ||
ou, ainda, | |||
<center><math> | |||
f^{n}_{i,j} = \left(2-4a\right)f^{n-1}_{i,j} - f^{n-2}_{i,j} + a\left(f^{n-1}_{i-1,j}+f^{n-1}_{i+1,j}+f^{n-1}_{i,j-1}+f^{n-1}_{i,j+1}\right), \qquad a\equiv \left(v\frac{\Delta t}{\Delta x}\right)^2. | |||
</math></center> | |||
=== Condições Iniciais === | |||
Para implementar o esquema acima, são necessários valores de <math>f</math> nos dois primeiros passos temporais. As condições iniciais para a equação da onda, no entanto, têm a forma | |||
<center><math> | <center><math> | ||
f(x,y,t=0) =\phi(x,y)=\phi_{i,j},\qquad f_t(x, y, t=0)=\psi(x,y)=\psi_{i,j}. | |||
</math></center> | </math></center> | ||
Desse modo, os valores da intensidade da onda no primeiro passo temporal, <math>f^0_{i,j}</math>, podem ser obtidos da primeira condição inicial: <math>f^0_{i,j}=\phi_{i, j}</math>. Os valores da intensidade da onda no segundo passo temporal podem ser aproximados como se segue: visto que | |||
<center><math> | <center><math> | ||
f_t(x,y,t=0)\approx | |||
\frac{f(x, y, t=0)}{\Delta t}, | |||
</math></center> | </math></center> | ||
então, em notação discreta, | |||
<center><math> | |||
\psi_{i,j}\approx | |||
\frac{f^{0}_{i,j}}{\Delta t}. | |||
</math></center> | |||
A diferença central desse quociente é | |||
=== Contorno | <center><math> | ||
\frac{f^{0}_{i,j}}{\Delta t}\approx\frac{f^{1}_{i,j}-f^{-1}_{i,j}}{2\Delta t}. | |||
</math></center> | |||
Assim, | |||
<center><math> | |||
\psi_{i,j}\approx\frac{f^{1}_{i,j}-f^{-1}_{i,j}}{2\Delta t} | |||
\implies | |||
f^{1}_{i,j}-f^{-1}_{i,j}=2\Delta t\psi_{i,j} | |||
. | |||
</math></center> | |||
Além disso, para <math>n=1</math>, a última equação do esquema FTCS resulta em | |||
<center><math> | |||
f^1_{i,j} = \left(2-4a\right)f^0_{i,j} + a\left(f^{0}_{i-1,j}+f^{0}_{i+1,j}+f^{0}_{i,j-1}+f^{0}_{i,j+1}\right) - f^{-1}_{i,j}. | |||
</math></center> | |||
Portanto, tem-se o sistema | |||
<center><math> | |||
\begin{cases} | |||
f^1_{i,j} - f^{-1}_{i,j} = 2\Delta t\psi_{i,j}\\ | |||
f^1_{i,j} + f^{-1}_{i,j} = \left(2-4a\right)f^0_{i,j} + a\left(f^{0}_{i-1,j}+f^{0}_{i+1,j}+f^{0}_{i,j-1}+f^{0}_{i,j+1}\right) \end{cases}. | |||
</math></center> | |||
Somando as duas equações, obtém-se uma expressão para <math>f^1_{i,j}</math>: | |||
<center><math> | |||
f^1_{i,j} = \Delta t\psi_{i,j} + \left(1-2a\right)f^0_{i,j} + \frac{a}{2}\left(f^{0}_{i-1,j}+f^{0}_{i+1,j}+f^{0}_{i,j-1}+f^{0}_{i,j+1}\right). | |||
</math></center> | |||
== Implementações em Python == | |||
=== Pulso em Repouso === | |||
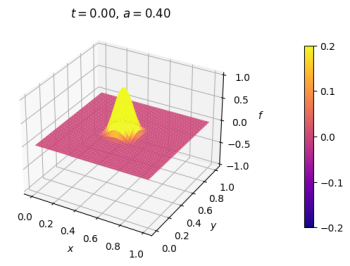
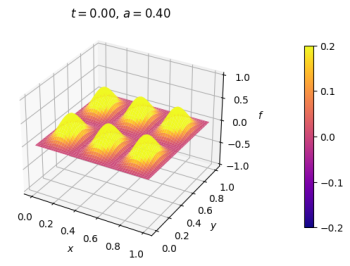
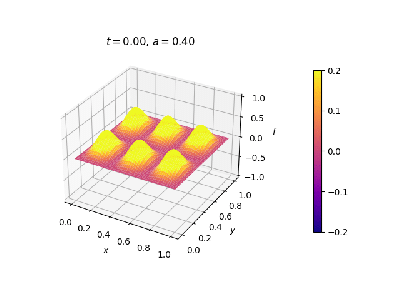
==== Exemplo 1 ==== | |||
[[Malha quadrada, pulso senoidal em repouso no centro. Contornos fixos.]] | |||
<center> | |||
{| | |||
|[[Arquivo:onda2dCI.png|thumb|upright=0.0|center|Onda no estado inicial.|350px]] | |||
|[[Arquivo:onda2d.gif|thumb|upright=0.0|center|Evolução temporal.|400px]] | |||
|} | |||
</center> | |||
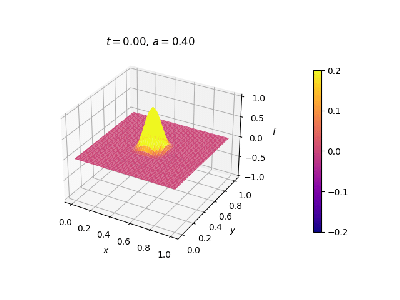
==== Exemplo 2 ==== | |||
[[Malha quadrada, pulso em repouso próximo à fronteira. Contorno fixo.]] | |||
<center> | |||
{| | |||
|[[Arquivo:onda2dNFCI.png|thumb|upright=0.0|center|Onda no estado inicial.|350px]] | |||
|[[Arquivo:onda2dNF.gif|thumb|upright=0.0|center|Evolução temporal.|400px]] | |||
|} | |||
</center> | |||
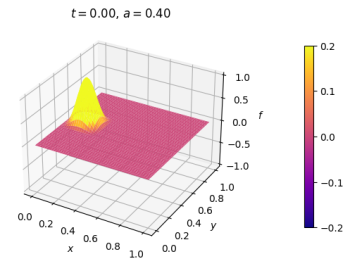
==== Exemplo 3 ==== | |||
[[Malha quadrada, diversos pulsos em repouso. Contorno fixo.]] | |||
<center> | |||
{| | |||
|[[Arquivo:onda2dsen2CI.png|thumb|upright=0.0|center|Onda no estado inicial.|350px]] | |||
|[[Arquivo:onda2dsen2.gif|thumb|upright=0.0|center|Evolução temporal.|400px]] | |||
|} | |||
</center> | |||
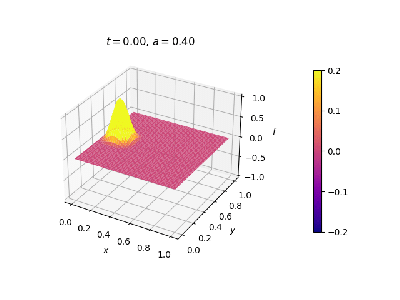
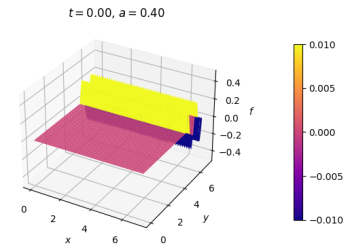
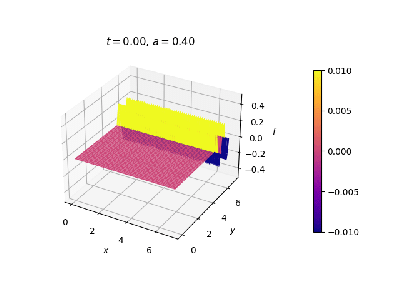
=== Simulação de Fenda Dupla === | |||
[[Malha quadrada, anel nas extremidades x e contorno fixo em y. Anteparo paralelo ao eixo x.]] | |||
<center> | |||
{| | |||
|[[Arquivo:duplafendaCI.png|thumb|upright=0.0|center|Onda no estado inicial.|350px]] | |||
|[[Arquivo:duplafenda.gif|thumb|upright=0.0|center|Evolução temporal.|400px]] | |||
|} | |||
</center> | |||
= Apêndice A: Métodos numéricos para solução da equação de advecção = | = Apêndice A: Métodos numéricos para solução da equação de advecção = | ||
| Linha 473: | Linha 644: | ||
[[Comparação dos métodos numéricos]] | [[Comparação dos métodos numéricos]] | ||
= Referências = | |||
#Elmore, C. W. e Head, M. A. 2012. '''Physics of Waves.'''. Dover, New York. ISBN, 0486140652, 9780486140650. | |||
#Régis S. '''Métodos numéricos para solução da equação de transporte de massa'''. Instituto de Pesquisas Hidráulicas - UFRGS.(regis.pereira@ufrgs.br). https://semengo.furg.br/images/2006/31.pdf | |||
#Miranda, Ivan. 2021.'''Métodos de diferenças finitas para a equação da onda acústica em meios heterogêneos'''. Escola de Engenharia - UFF.https://app.uff.br/riuff/bitstream/handle/1/22069/Ivan%20Miranda%20de%20Almeida%20-%20TCC%20-%20com_ficha.pdf?sequence=1&isAllowed=y | |||
#Lorranne, Dayvenne. 2020.'''Uma simulação da equação da onda unidimensional pelo método das diferenças finitas: formulação explícita'''.Escola de Ciências Exatas e da computação -PUCGoiás. https://repositorio.pucgoias.edu.br/jspui/bitstream/123456789/1211/1/Monografia%20Dayvenne%20Lorranne%20%281%29.pdf | |||
#Grigoryan V. 2012. '''Finite differences for the wave equation'''. University of California, Santa Barbara. https://web.math.ucsb.edu/~grigoryan/124B/lecs/lec18.pdf | |||
Edição atual tal como às 12h09min de 3 de março de 2024
Filssen Schereiber, João Roth e Lucas Oliveira
Este trabalho tem como objetivo realizar um estudo introdutório da equação da onda, adotando uma abordagem computacional que proporciona uma base teórica sólida e intuitiva. Inicialmente, é realizada a implementação de uma solução numérica (FTCS) para a equação da advecção, visando o estudo da propagação de uma perturbação e explorando aspectos computacionais fundamentais. Em seguida, a equação da onda é aplicada em uma dimensão, permitindo uma investigação detalhada de fenômenos ondulatórios, tais como reflexão, interferência e refração. A abordagem é estendida para duas dimensões, incluindo a análise dos efeitos de contorno nesse contexto. Por fim, o trabalho aprofunda-se no estudo do fenômeno de difração, contribuindo para uma compreensão mais enriquecedora dos aspectos complexos dos fenômenos ondulatórios em múltiplas dimensões.
Introdução
O que é uma onda exatamente? De acordo com 'A Student’s Guide to Waves', a literatura apresenta diversas definições. Contudo, a característica mais comum que define uma onda é sua natureza como uma perturbação, uma alteração no estado de equilíbrio que, inicialmente, permanece inalterado. Quando uma fonte externa, como um objeto vibrante ou uma força inicial, perturba a condição de equilíbrio de um meio, essa perturbação é transmitida de partícula para partícula ao longo do meio. Esse processo de transmissão de energia ocorre sem que as partículas individuais do meio se desloquem significativamente de suas posições de equilíbrio. Em outras palavras, a energia da perturbação é transferida, mas as partículas do meio não se movem em conjunto com a onda.
O estudo da física das ondas desempenha um papel crucial, permeando inúmeras áreas da ciência e da tecnologia ao proporcionar uma compreensão profunda dos fenômenos ondulatórios e suas aplicações práticas. A física das ondas desempenha um papel essencial em nossa vida cotidiana. Seu impacto é evidente na tecnologia de comunicação, onde as ondas de rádio e micro-ondas são a espinha dorsal de redes globais de telefonia móvel e internet sem fio.
Com base no exposto, propõe-se a realização de um estudo abrangente sobre a modelagem de fenômenos ondulatórios. Inicialmente, serão apresentados pontos importantes acerca da equação da onda. Em seguida, dedicaremos atenção ao estudo da propagação de uma perturbação a partir da equação de advecção. Nesse contexto, abriremos a discussão sobre a abordagem computacional, e, tangencialmente, comentaremos sobre outros métodos numéricos para resolver a advecção. Posteriormente, faremos um estudo sobre a solução numérica da equação da onda, permitindo a modelagem de fenômenos ondulatórios, como reflexão, interferência, refração e difração.
Equação da Onda
A função de uma onda é aquela que especifica o valor da perturbação em cada ponto e instante ao longo de seu percurso. Para iniciar nossa análise, abordaremos o exemplo mais simples, em que a propagação ocorre unicamente em uma direção, como é o caso das ondas transversais em uma corda.
Dedução
O perfil da onda em uma corda em um determinado instante é equivalente à forma que a corda apresenta nesse momento, que é dada pela função . A perturbação assume a forma de uma onda progressiva, movendo-se como uma entidade coesa para a direita, mantendo sua configuração inalterada, com velocidade . Dessa forma, ao acompanhar a onda em um referencial inercial diferente, em que , onde representa o antigo deslocado por , a relação entre os dois referenciais é estabelecida por
de modo que, no referencial original,
descreve uma onda progressiva, que se propaga para a direita, com velocidade .
Para associar uma equação de movimento com a propagação da onda, vamos calcular a aceleração num dado ponto . A velocidade e a aceleração em se obtêm fixando e derivando em relação ao tempo, o que corresponde a tomar derivadas parciais.
pela regra da cadeia
Analogamente,
ou seja,
Derivando em relação a obtemos que:
Assim,
Denominada equação da onda unidimensional, esta é uma das equações fundamentais da física.
Solução Analítica
Agora, procederemos à análise do movimento de uma corda de comprimento que vibra com extremidades fixas. Como essas extremidades são fixas, temos, nos pontos e , os valores .
Além disso, supomos que a função e para .
Com base nas observações realizadas, torna-se possível identificar um conjunto fundamental de soluções por meio da aplicação do método de separação de variáveis.
Suponhamos que existam duas soluções, uma dependendo exclusivamente de e outra exclusivamente de , de modo que possamos expressar a função como o produto dessas duas.
Assim, podemos escrever as derivadas parciais como
substituindo na equação da onda,
Dessa forma, torna-se evidente que a razão entre as funções de consiste em uma constante, assim como .
(I)
(II)
Observa-se que as equações (I) e (II) são equações diferenciais ordinárias (EDOs) lineares de segunda ordem, cujos coeficientes podem depender da variável independente e, potencialmente, serem funções não constantes. Assim, é possível usarmos das condições de contorno para resolver essas equações.
Resolvendo a Equação (I)
Se avaliarmos as condições de contorno para os possíveis valores de lambda, que devem ser maiores ou iguais a zero, obtemos apenas a solução trivial. Contudo, se lambda for negativo, surge uma solução para na forma
Avaliando as condições de contorno, temos:
Certamente, observa-se que, para alcançarmos uma solução não trivial, é necessário que , onde .
Resolvendo a Equação (II)
Analogamente, temos uma solução não trivial para lambda menor que zero.
Voltando para a solução geral:
Juntando as constantes
Avaliando as condições iniciais:
Para , temos
É possível observar que representa uma série de Fourier de senos, na qual os coeficientes são determinados por:
Avaliando :
Analogamente a , é uma série de Fourier de senos. Portanto, podemos determinar da seguinte maneira:
Implementação da Solução Analítica
Se considerarmos 10 como o número máximo de termos na série de Fourier de uma corda com comprimento e velocidade , é possível criar um mapa da amplitude em função das posições de cada ponto da corda e do tempo. Esse tipo de gráfico será recorrente em nossa análise em diferentes casos.
Neste caso, é possível observar que inicialmente a corda possui um máximo localizado no centro do eixo de posição, com mínimos iguais a zero nas extremidades do eixo. À medida que a função evolui no tempo, a amplitude diminui, passando por um instante onde em todos os pontos da corda a amplitude é zero, e prossegue para completar um meio período, onde apresenta um mínimo menor que zero centrado no eixo x e máximos iguais a zero nas extremidades da corda.
A equação de advecção unidimensional
Partimos da equação de advecção para estudarmos a propagação de uma perturbação.
A equação de onda está intimamente relacionada à chamada equação de advecção, que, em uma dimensão, assume a seguinte forma:
A equação a seguir descreve a advecção passiva de um campo escalar transportado por um fluxo de velocidade constante . Como a equação de advecção é um tanto mais simples do que a equação da onda, discutiremos aquela em primeiro lugar. A equação de advecção possui a solução formal:
Essa solução descreve um pulso de forma arbitrária que é arrastado pelo fluxo a uma velocidade constante , sem alterar sua forma.
Esquema FTCS para equação da advecção
Para a abordagem numérica computacional do nosso estudo, utilizamos o esquema FTCS (Forward Time-Centered Space).
O método FTCS é amplamente empregado na resolução de equações diferenciais parciais. Trata-se de um método de diferenças finitas que adota uma abordagem explícita no tempo e central no espaço. Esse esquema apresenta uma acurácia de primeira ordem no tempo e de segunda ordem no espaço.
A discretização no tempo (Forward Time) pode ser feita utilizando a diferença finita para a derivada temporal:
onde representa a amplitude da perturbação no ponto do espaço e no instante , e é o passo de tempo.
A discretização no espaço (Central Space) pode ser feita utilizando a diferença finita para a derivada espacial:
onde é o espaçamento entre os pontos discretizados no espaço.
As equações acima podem ser reescritas como
onde .
Análise de estabilidade de von Neumann
A análise de estabilidade de von Neumann é uma abordagem teórica utilizada para avaliar a estabilidade numérica de esquemas de diferenças finitas, incluindo o esquema FTCS. Usando o método de von Neumann, supõe-se a seguinte solução tentativa para a EDP:
onde , é o número de onda, e é a amplitude da onda, uma função do tempo.
Assim, a solução no passo de tempo e em é escrita como
Substituindo esta solução tentativa na expressão da advecção discretizada temos:
(III)
Seja a razão da amplitude da onda no passo de tempo em relação ao passo . Portanto,
Dividir (III) por resulta em
Se dividirmos esse resultado por temos:
Assim,
Isso implica que independentemente do passo de tempo selecionado ou do passo espacial , portanto, FTCS é incondicionalmente instável.
Apesar de ser incondicionalmente instável, o esquema funcionará bem em nossa modelagem, uma vez que o método apresenta também suas vantagens. O esquema FTCS é relativamente simples de implementar, o que facilita sua aplicação, principalmente para problemas bidimensionais ou tridimensionais, como pretendemos abordar posteriormente.
Em alguns casos específicos, o FTCS pode ser computacionalmente eficiente. Se a equação diferencial parcial for relativamente simples e o domínio de interesse for bem comportado, o FTCS pode oferecer uma solução razoável com custo computacional relativamente baixo.
É feita uma comparação entre outros métodos numéricos de diferenças finitas para solução da equação da advecção e comparado o erro relativo à solução analítica no Apêndice A.
Implementação do esquema FTCS
Vamos agora examinar a implementação do esquema FTCS na equação da advecção para visualizarmos a propagação de uma perturbação na forma de em um eixo infinito. Em outras palavras:
- Condição inicial: ;
- Condições de contorno periódicas.
Neste caso, podemos observar uma perturbação se propagando no sentido negativo do eixo sem perda de amplitude ou mudança de forma. Isso acontece porque, com a equação da advecção, podemos analisar apenas a cinemática de uma perturbação, a qual, por sua vez, apenas relaciona os atributos como amplitude, comprimento de onda, frequência e velocidade.
Podemos observar, ainda, que a amplitude está relacionada à condição inicial em que o máximo de é atingido quando . Nesse contexto, considerando , percebemos que ocorre exatamente no meio do eixo. Em consequência, a amplitude máxima, que é 2, é inicialmente alcançada no ponto central do eixo .
A equação da onda em uma dimensão
A equação da onda, que em uma dimensão assume a forma
onde geralmente é algum tipo de deslocamento ou perturbação, enquanto é a velocidade da onda. A equação de onda possui a solução formal
onde e são funções arbitrárias. A solução acima representa pulsos de onda de formato arbitrário que se propagam com velocidade nas direções e , respectivamente, sem alterar a forma.
Esquema FTCS para equação da onda unidimensional
Iniciamos o estudo da solução numérica da equação da onda a partir da implementação do esquema FTCS, pois, como comentado antes, este é o método de implementação mais prático para generalizarmos para mais dimensões espaciais.
As derivadas de segunda ordem podem ser substituídas por diferenças centrais. A aproximação de diferença mais amplamente utilizada para a derivada de segunda ordem é
Uma aproximação semelhante para a derivada de segunda ordem na direção é dada por
Agora podemos substituir as derivadas e obter
Assumimos que e já foram calculados para . A única quantidade desconhecida é, portanto, , que podemos resolver da seguinte forma:
onde introduzimos o parâmetro
conhecido como número de Courant.
Análise de estabilidade de von Neumann
Pela análise de Von Neumann, substituímos por na equação da onda. Após manipulações, a expressão resultante é:
Usando a identidade de Euler , chegamos a:
Reescrevendo , a equação torna-se:
Expressamos isso como , onde . As raízes são:
Se , implica . Se , pela condição de Von Neumann, tornando o método condicionalmente estável pela condição CFL.
Reflexão de onda em uma corda
Quando uma onda se propaga ao longo de uma corda e incide em uma de suas extremidades, ocorre a sua reflexão. Ao atingir um extremo fixo, que não pode oscilar, é possível observar que o pulso refletido apresenta uma orientação oposta à do pulso incidente. Podemos afirmar que o pulso reflete com inversão de fase, pois isso ocorre devido à reação do ponto fixo sobre a corda com uma força de mesmo módulo. Uma situação distinta ocorre quando a extremidade da corda é móvel, ou seja, não há troca de forças entre ela e a corda, resultando em uma reflexão sem inversão de fase.
Além disso, em um sistema fechado e sem dissipação de energia, podemos observar que as ondas refletidas, independentemente da fase, sofrem interferência construtiva e produzem picos de máximo ou mínimo, dependendo do contexto.
Podemos observar esse fenômeno ao implementar a solução da equação da onda unidimensional com condições de contorno fixas e periódicas, respectivamente, para uma corda com extremidades fixas e extremidades móveis.
Perturbação em uma corda com extremidades fixas
Neste caso, é possível observar que a corda iniciará a partir do seu ponto mais alto no centro do eixo. A perturbação se propagará igualmente para ambos os sentidos do eixo. Ao atingir as extremidades fixas, as duas perturbações, invertidas, deslocam-se em direção ao centro da corda, onde interferem de forma construtiva e produzem um mínimo de amplitude.
Perturbação em uma corda com extremidades móveis
Com extremidades móveis, não se observa uma mudança de fase da perturbação inicial ao atingir os extremos da corda. No entanto, ao implementarmos condições de contorno periódicas, implicamos que, ao alcançar uma das extremidades da corda, o pulso retorna à outra extremidade, continuando a se propagar na mesma direção e com a mesma velocidade. Como a perturbação inicial gera dois pulsos se propagando em direções opostas a partir do centro do eixo, com velocidades iguais, percebemos a interação construtiva dos pulsos que alcançam os limites do eixo simultaneamente. Isso faz com que retornem a se propagar em direção ao centro, gerando máximos de amplitude em cada interação.
Alteração no meio de propagação
A refração é um fenômeno que ocorre quando uma onda passa de um meio para outro com uma velocidade de propagação diferente. Esse fenômeno é mais comumente associado a ondas de luz, mas também pode ocorrer com ondas sonoras, ondas de rádio, ondas sísmicas e outras formas de ondas.
Se uma onda se propaga em uma corda e encontra uma mudança abrupta nas propriedades da corda, como a densidade ou a tensão, isso pode resultar em uma mudança na velocidade da onda. O grau de refração dependerá das diferenças nas propriedades do meio antes e depois da mudança.
Em um modelo que considera a reflexão e a refração na junção das duas ondas [Elmore e Head], é demonstrado que a razão entre as amplitudes da onda refratada () e a amplitude da onda incidente () é dada por:
Usando a relação da velocidade de propagação com as variáveis de tensão e densidade podemos chegar em expressões para as amplitudes do pulso que irá voltar () e do pulso que irá passar para a outra corda ().
(IV)
onde é a amplitude do pulso incidente.
No nosso caso, a perturbação inicial tem amplitude de 1, porém propaga-se isotopicamente nos dois sentidos do eixo x. O pulso que se desloca no sentido negativo do eixo interage imediatamente com o ponto fixo da corda e torna a propagar-se no sentido positivo, mas agora com uma fase. Assim, temos dois pulsos, um positivo e um negativo, ambos com amplitude igual a , propagando-se em direção a outra corda de densidade diferente.
Com as velocidades de propagação nos dois meios, utilizando as fórmulas em (IV), podemos determinar que a amplitude do pulso que irá voltar é , enquanto a do pulso que será refratado é .
Oscilador em uma corda
Agora, em vez de variarmos as condições de contorno para um pulso senoidal em uma corda, estamos avaliando um oscilador senoidal acoplado a corda com parâmetros físicos bem definidos: amplitude (A), frequência (f) e comprimento de onda ( λ ). Assim, ao invés de termos uma condição inicial que aplicada em um pequena porção da corda se propaga, iremos avaliar um oscilador da forma que define a amplitude inicial para cada ponto da corda, onde é o número de onda definido como duas vezes sobre o comprimento de onda. Vale notar ainda que λ é uma função da velocidade de propagação (propriedade da corda) e da frequência (propriedade do oscilado).
Seja , e , que resulta em um comprimento de onda igual a 7.7. Implementando um oscilador com esses parâmetros para uma corda com extremidades fixas, obtemos
Observamos que, ao ajustar arbitrariamente os parâmetros do oscilador, obtemos regiões mais escuras e mais claras, pouco organizadas. Nessas regiões, ocorrem interferências destrutivas e construtivas, respectivamente. As interferências ocorrem de forma pouco definida, uma vez que não há, nesse caso, um padrão bem definido para as interações que a onda sofrerá. No entanto, veremos que isso pode ser modificado.
Ondas estacionárias
A relação entre o comprimento de onda da onda incidente ( λ) e a distância disponível para a onda se refletir (, onde é o comprimento da região confinada, da corda) deve permitir a formação de nós e ventres estacionários. Para ondas estacionárias em uma corda com extremidades fixas, os comprimentos de onda permitidos são dados por , onde é um número inteiro positivo.
Essa fórmula mostra que à medida que aumenta, o comprimento de onda diminui. Cada valor de corresponde a uma harmônica específica, que representa o número de meios comprimentos de onda que cabem na corda. A primeira harmônica () tem um nó em cada extremidade da corda, a segunda harmônica () tem dois nós, e assim por diante.
Dado que e , é possível expressar um conjunto discreto de frequências para o nosso oscilador, as quais resultam em ondas estacionárias.
Dessa forma, podemos aplicar valores de condicionados a gerar as condições necessárias para a formação de ondas estacionárias.
A Equação da Onda em Duas Dimensões
Agora, procederemos à avaliação da modelagem de ondas em duas dimensões. Nesse contexto, além dos fenômenos já observados, é possível perceber também a difração.
Esquema FTCS para Equação da Onda Bidimensional
Em duas dimensões, a equação da onda é dada por
Aproximando todas as derivadas parciais por uma diferença finita centrada, segue que
Portanto, em forma discreta, a equação da onda pode ser escrita como
Para , segue que
ou, ainda,
Condições Iniciais
Para implementar o esquema acima, são necessários valores de nos dois primeiros passos temporais. As condições iniciais para a equação da onda, no entanto, têm a forma
Desse modo, os valores da intensidade da onda no primeiro passo temporal, , podem ser obtidos da primeira condição inicial: . Os valores da intensidade da onda no segundo passo temporal podem ser aproximados como se segue: visto que
então, em notação discreta,
A diferença central desse quociente é
Assim,
Além disso, para , a última equação do esquema FTCS resulta em
Portanto, tem-se o sistema
Somando as duas equações, obtém-se uma expressão para :
Implementações em Python
Pulso em Repouso
Exemplo 1
Malha quadrada, pulso senoidal em repouso no centro. Contornos fixos.
Exemplo 2
Malha quadrada, pulso em repouso próximo à fronteira. Contorno fixo.
Exemplo 3
Malha quadrada, diversos pulsos em repouso. Contorno fixo.
Simulação de Fenda Dupla
Malha quadrada, anel nas extremidades x e contorno fixo em y. Anteparo paralelo ao eixo x.
Apêndice A: Métodos numéricos para solução da equação de advecção
Método Lax-Wendroff de dois passos
Comparação dos métodos numéricos
Referências
- Elmore, C. W. e Head, M. A. 2012. Physics of Waves.. Dover, New York. ISBN, 0486140652, 9780486140650.
- Régis S. Métodos numéricos para solução da equação de transporte de massa. Instituto de Pesquisas Hidráulicas - UFRGS.(regis.pereira@ufrgs.br). https://semengo.furg.br/images/2006/31.pdf
- Miranda, Ivan. 2021.Métodos de diferenças finitas para a equação da onda acústica em meios heterogêneos. Escola de Engenharia - UFF.https://app.uff.br/riuff/bitstream/handle/1/22069/Ivan%20Miranda%20de%20Almeida%20-%20TCC%20-%20com_ficha.pdf?sequence=1&isAllowed=y
- Lorranne, Dayvenne. 2020.Uma simulação da equação da onda unidimensional pelo método das diferenças finitas: formulação explícita.Escola de Ciências Exatas e da computação -PUCGoiás. https://repositorio.pucgoias.edu.br/jspui/bitstream/123456789/1211/1/Monografia%20Dayvenne%20Lorranne%20%281%29.pdf
- Grigoryan V. 2012. Finite differences for the wave equation. University of California, Santa Barbara. https://web.math.ucsb.edu/~grigoryan/124B/lecs/lec18.pdf








































































































![{\displaystyle g^{2}-2[1-{\frac {C}{2}}(1-\cos \theta )]g+1=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88882dbbaa1eb9606c60f7f0b128ae8c3d340fff)




































![{\displaystyle f_{i,j}^{n+1}=2f_{i,j}^{n}-f_{i,j}^{n-1}+v^{2}\left[{\frac {\Delta t^{2}}{\Delta x^{2}}}\left(f_{i+1,j}^{n}-2f_{i,j}^{n}+f_{i-1,j}^{n}\right)+{\frac {\Delta t^{2}}{\Delta y^{2}}}\left(f_{i,j+1}^{n}-2f_{i,j}^{n}+f_{i,j-1}^{n}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e461f419927f9c16810c5d5b4e2966db4323201e)