Upwind Differencing
Foram apresentados métodos numéricos eficientes com propósitos gerais para resolver a equação de advecção. Entretanto, é necessário restringir nossa abordagem a formas de onda suficientemente suaves para evitar oscilações espúrias tanto nas bordas de ataque quanto nas bordas de queda da forma de onda. Uma abordagem reconhecida para suprimir desvios nas extremidades inicial e final de uma forma de onda afiada é a adoção de um esquema conhecido como "esquema de diferenças upwind".
Nesse esquema, as diferenças espaciais são inclinadas na direção "upwind", ou seja, na direção de onde o fluxo advectivo se origina.
Portanto, a versão upwind do simples esquema de diferenças explícitas é escrita da seguinte forma:
Para :
(1)
Para :
(2)
Combinando (1) e (2):
(3)
Onde
e
O esquema upwind é estável quando a seguinte condição Courant-Friedrichs-Lewy (CFL) é atendida:
Implementação do método
- Condição inicial: ;
- Condições de contorno para bordas cíclicas.
# Solução pelo método Upwind para equação de advecção
def Upwindad(L, tf, v, Nx, Nt):
"""
Parâmetros:
- L: comprimento
- tf: tempo final
- v: velocidade de propagação
- Nx: número de pontos na direção espacial
- Nt: número de pontos na direção temporal
Retorna:
- Matriz com a solução da equação da onda
"""
dx = L / (Nx - 1)
dt = tf / (Nt - 1)
r = v * dt / dx
u = np.zeros((Nt, Nx+1))
# Condição inicial: u(x,0) = f(x)
x = np.linspace(0, L, Nx+1)
u[0,:] = 1 - np.cos(x) # Função que descreve a perturbação da onda
# Condições de contorno borda infinita:
xpos = np.zeros(Nx+1)
xneg = np.zeros(Nx+1)
for i in range(0, Nx+1):
xpos[i] = i+1
xneg[i] = i-1
xpos[Nx] = 0
xneg[0] = Nx
# Iteração no tempo
for n in range(0, Nt - 1):
for i in range(0, Nx+1):
v_mais = np.maximum(v, 0)
v_menos = np.minimum(v, 0)
u_x_mais = 1/dx * (u[n, int(xpos[i])] - u[n, i])
u_x_menos = 1/dx * (u[n, i] - u[n, int(xneg[i])])
u[n+1, i] = u[n, i] - dt * (v_mais * u_x_menos + v_menos * u_x_mais)
return u
# Parâmetros
L = 2*np.pi
tf =1
v = -1 # -1. muda direção de propagação
Nx = 100
Nt = 500
solv4 = Upwindad(L, tf, v, Nx, Nt)
listX = np.linspace(0, L, Nx+1)
listT = np.linspace(0, tf, Nt)
X, T = np.meshgrid(listX, listT)
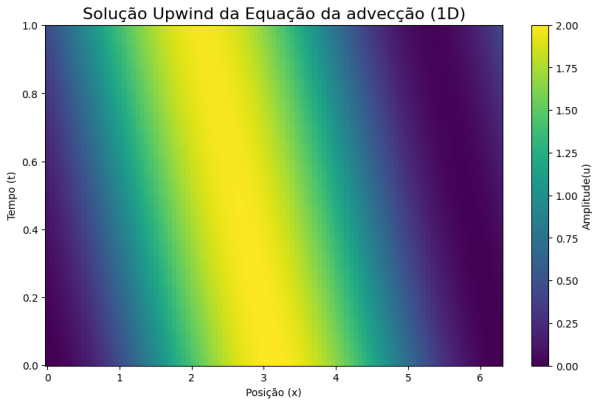
plt.figure(figsize=(10, 6))
plt.pcolormesh(X, T, solv4, cmap='viridis', shading='auto')
plt.colorbar(label='Amplitude(u)')
plt.xlabel('Posição (x)')
plt.ylabel('Tempo (t)')
plt.title('Solução Upwind da Equação da advecção (1D)', fontsize=16)
plt.show()
# Teste: Plota todas as cuvas amplitude por posição de todos os tempos:
for tt in range(len(listT-1)):
amplitudes_tt = solv4[ tt,:]
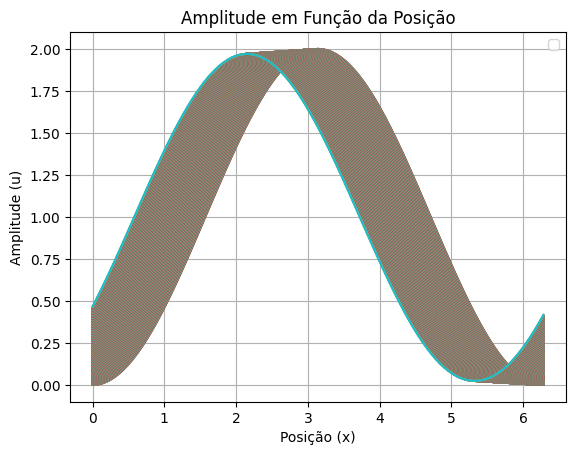
plt.plot(listX, amplitudes_tt)
plt.title('Amplitude em Função da Posição')
plt.xlabel('Posição (x)')
plt.ylabel('Amplitude (u)')
plt.legend()
plt.grid(True)
plt.show()