Métodos de Lyapunov: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| (Uma revisão intermediária pelo mesmo usuário não está sendo mostrada) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[Linearização de sistemas de equações não lineares]] |[[ | {{Ecologia| [[Linearização de sistemas de equações não lineares]] |[[Introdução à equações diferenciais com atraso]]}} | ||
Os critérios de Lyapunov para analisar a estabilidade em sistemas não lineares são: | Os critérios de Lyapunov para analisar a estabilidade em sistemas não lineares são: | ||
| Linha 47: | Linha 47: | ||
Temos os seguintes autovalores <math>\left\{ -0.37,5.37\right\} </math> com os seguintes autovetores correspondentes <math>\left\{ \left(1,-0.69\right),\left(1,2.19\right)\right\} </math>. Então significa que na direção <math>\left(1,-0.69\right)</math> o sistema evolui de forma a se aproximar da origem (autovalor negativo) e na direção <math>\left(1,2.19\right)</math> se afasta da da origem (autovalor positivo). | Temos os seguintes autovalores <math>\left\{ -0.37,5.37\right\} </math> com os seguintes autovetores correspondentes <math>\left\{ \left(1,-0.69\right),\left(1,2.19\right)\right\} </math>. Então significa que na direção <math>\left(1,-0.69\right)</math> o sistema evolui de forma a se aproximar da origem (autovalor negativo) e na direção <math>\left(1,2.19\right)</math> se afasta da da origem (autovalor positivo). | ||
Ou ainda em uma explicação mais geral, uma matriz <math>A</math> qualquer que tenha os autovalores <math>\lambda_{i}</math> associado aos autovetores <math>\left|\lambda_{i}\right\rangle</math>: | |||
<math display="block">A=\sum_{i}\lambda_{i}\left|\lambda_{i}\right\rangle \left\langle \lambda_{i}\right|</math> | |||
Então escrevendo nosso sistema linear de equações diferenciais como: | |||
<math display="block">\left|\dot{x}\right\rangle =A\left|x\right\rangle </math> | |||
Ou ainda: | |||
<math display ="block"> \left|\dot{x}\right\rangle =\sum_{i}\lambda_{i}\left|\lambda_{i}\right\rangle \left\langle \lambda_{i}|x\right\rangle </math> | |||
Podemos pensar então que o termo <math>\left\langle \lambda_{i}|x\right\rangle</math> nos dá uma medida de ortogonalidade entre nosso ponto atual <math> \left|x\right\rangle </math> e o autovetor <math>\left|\lambda_{i}\right\rangle</math> , o que implica em 'quanto' nosso sistema vai se mover na direção apontada pelo autovalor. Como um extremo, podemos ver que se forem perpendiculares entre si, então <math>\left\langle \lambda_{i}|x\right\rangle =0 </math> logo o termo inteiro do somatório é zerado. Uma vez que <math>\left\langle \lambda_{i}|x\right\rangle \neq0</math>, então resta o vetor <math>\left|\lambda_{i}\right\rangle</math>, que vai dar efetivamente a direção no qual o ponto vai se mover. E ainda por fim, temos <math>\lambda_{i}</math> que vai regular o sentido no qual o sistema vai se 'mover'. Podemos perceber aqui, para valores reais, a necessidade de que todos os autovalores sejam negativos para termos um sistema estável, assim como o motivo de que os autovalores reais positivos configuram um sistema instável. | |||
Obs. Esta é uma notação emprestada da mecânica quântica, a notação de dirac. Onde <math>\left\langle \lambda_{i}\right|</math> é o transposto conjugado de <math>\left|\lambda_{i}\right\rangle</math> e <math>\left\langle \lambda_{i}|\lambda_{j}\right\rangle</math> denota o produto interno entre os vetores <math>\left|\lambda_{i}\right\rangle</math> e <math>\left|\lambda_{j}\right\rangle</math>. | |||
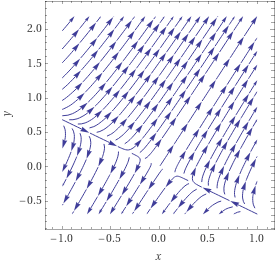
[[Ficheiro:Wolfafa.gif|miniaturadaimagem|Diagrama de fase gerado no [https://www.wolframalpha.com/input/?i=StreamPlot%5B+%7Bx%2B2y%2C3x%2B4y%7D+%2C%7Bx%2C-1%2C1%7D%2C%7By%2C-0.69%2C2.19%7D%5D WolframAlpha] para o sistema formado por <math>\dot{x}=x+2y</math> e <math>\dot{y}=3+4y</math>.|alt=]] | [[Ficheiro:Wolfafa.gif|miniaturadaimagem|Diagrama de fase gerado no [https://www.wolframalpha.com/input/?i=StreamPlot%5B+%7Bx%2B2y%2C3x%2B4y%7D+%2C%7Bx%2C-1%2C1%7D%2C%7By%2C-0.69%2C2.19%7D%5D WolframAlpha] para o sistema formado por <math>\dot{x}=x+2y</math> e <math>\dot{y}=3+4y</math>.|alt=]] | ||
| Linha 190: | Linha 207: | ||
<references /> | <references /> | ||
{{Ecologia| [[Linearização de sistemas de equações não lineares]] |[[ | {{Ecologia| [[Linearização de sistemas de equações não lineares]] |[[Introdução à equações diferenciais com atraso]]}} | ||
Edição atual tal como às 23h39min de 9 de novembro de 2022
Anterior: Linearização de sistemas de equações não lineares | Índice: Ecologia | Próximo: Introdução à equações diferenciais com atraso
Os critérios de Lyapunov para analisar a estabilidade em sistemas não lineares são:
- Primeiro critério de Lyapunov (método reduzido, método indireto ou teorema da linearização): a análise de estabilidade de um ponto de equilíbrio é feito estudando a estabilidade do sistema linearizado correspondente na vizinhança deste ponto de equilíbrio.
- Segundo critério de Lyapunov (método direto): a análise de estabilidade de um ponto de equilíbrio é feito usando funções escalares apropriadas definidas no espaço de estados.
Primeiro critério
Considerando uma função contínua:
Considerando a vizinhança do ponto de equilíbrio na origem (qualquer ponto pode ser transladado para a origem), temos o seguinte correspondente sistema linearizado:
- Se todos os autovalores da matriz tem parte real negativa o ponto de equilíbrio é assintoticamente estável;
- Se ao menos um dos auto valores da matriz da matriz tem parte real positiva então o ponto instável;
- Se um dos autovalores está localizado no eixo imaginário, isto é, tem parte real nula, mas todos os outros autovalores são negativos (não há autovalor positivo e nem todos são negativos), não é possível concluir nada sobre a estabilidade do ponto.
- Para 2 dimensões se temos uma estabilidade não assintótica e se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{1}=\lambda_{2}} temos um caso degenerado.
Olhando um exemplo simples para entendermos melhor, vamos considerar um sistema autônomo em duas dimensões. Especificamente:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} \lambda_1 & 0\\ 0 & \lambda_2 \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)}
Considerando que os autovalores sejam números reais, a magnitude não é a característica mais importante dos autovalores, mas sim o sinal. Se ambos os autovalores tem sinal positivo, então o sistema vai se afastar da origem. Por exemplo, se o sistema está em um ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(1,-1\right)} do espaço de estados vai sofrer uma variação positiva na coordenada x, e negativa na coordenada y. Agora se ambos os autovalores são negativos temos um deslocamento no sentido contrário, ou seja, o sistema vai se aproximar da origem. E por fim, se o sistema tem um autovalor com cada sinal, então significa que em um eixo ele se aproxima e no outro se afasta (ponto de sela).
Olhando para os autovetores da nossa matriz, eles apontam exatamente na direção dos eixos (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \left(1,0\right),\left(0,1\right)\right\} } ), que foram as direções em que discutimos o comportamento do sistema. De maneira geral, tivéssemos uma matriz qualquer, analisaríamos então o comportamento do sistema na direção dos autovetores. Por exemplo para o sistema:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} \dot{x}\\ \dot{y} \end{array}\right)=\left(\begin{array}{cc} 1 & 2\\ 3 & 4 \end{array}\right)\left(\begin{array}{c} x\\ y \end{array}\right)}
Temos os seguintes autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ -0.37,5.37\right\} } com os seguintes autovetores correspondentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \left(1,-0.69\right),\left(1,2.19\right)\right\} } . Então significa que na direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(1,-0.69\right)} o sistema evolui de forma a se aproximar da origem (autovalor negativo) e na direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(1,2.19\right)} se afasta da da origem (autovalor positivo).
Ou ainda em uma explicação mais geral, uma matriz Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
qualquer que tenha os autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{i}}
associado aos autovetores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\lambda_{i}\right\rangle}
:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\sum_{i}\lambda_{i}\left|\lambda_{i}\right\rangle \left\langle \lambda_{i}\right|}
Então escrevendo nosso sistema linear de equações diferenciais como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\dot{x}\right\rangle =A\left|x\right\rangle }
Ou ainda:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\dot{x}\right\rangle =\sum_{i}\lambda_{i}\left|\lambda_{i}\right\rangle \left\langle \lambda_{i}|x\right\rangle }
Podemos pensar então que o termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \lambda_{i}|x\right\rangle} nos dá uma medida de ortogonalidade entre nosso ponto atual Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|x\right\rangle } e o autovetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\lambda_{i}\right\rangle} , o que implica em 'quanto' nosso sistema vai se mover na direção apontada pelo autovalor. Como um extremo, podemos ver que se forem perpendiculares entre si, então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \lambda_{i}|x\right\rangle =0 } logo o termo inteiro do somatório é zerado. Uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \lambda_{i}|x\right\rangle \neq0} , então resta o vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\lambda_{i}\right\rangle} , que vai dar efetivamente a direção no qual o ponto vai se mover. E ainda por fim, temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{i}} que vai regular o sentido no qual o sistema vai se 'mover'. Podemos perceber aqui, para valores reais, a necessidade de que todos os autovalores sejam negativos para termos um sistema estável, assim como o motivo de que os autovalores reais positivos configuram um sistema instável.
Obs. Esta é uma notação emprestada da mecânica quântica, a notação de dirac. Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \lambda_{i}\right|} é o transposto conjugado de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\lambda_{i}\right\rangle} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \lambda_{i}|\lambda_{j}\right\rangle} denota o produto interno entre os vetores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\lambda_{i}\right\rangle} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\lambda_{j}\right\rangle} .
Segundo critério
O segundo critério de Lyapunov geralmente é utilizando quando não podemos utilizar o primeiro (com autovalores negativos). Precisamos de algumas definições adicionais para estudá-lo, sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W} um subconjunto aberto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathcal{R}^{n}} contendo a origem (qualquer ponto de equilíbrio pode ser transladado para a origem), então uma função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V:W\rightarrow \mathcal{R}\text{ tal que }\boldsymbol{x}\mapsto V\left(\boldsymbol{x}\right)}
É [semi]positiva definida em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W} se:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}_{0}\right)=0}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)>0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[V\left(\boldsymbol{x}\right)\geq0\right]} , sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}\neq\boldsymbol{x}_{0}}
E [semi]definida negativa se:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}_{0}\right)=0}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)<0} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[V\left(\boldsymbol{x}\right)\leq0\right]} , sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}\neq\boldsymbol{x}_{0}} .
Vale a pena um olhar especial para funções quadráticas.
- 1 variável: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle f\left(x_{1}\right)=a_{11}x_{1}^{2}=x_{1}a_{11}x_{1}}
- 2 variáveis: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle f\left(x_{1},x_{2}\right)=x_{1}a_{11}x_{1}+x_{1}a_{12}x_{2}+x_{2}a_{21}x_{1}+x_{2}a_{22}x_{2}}
- N-variáveis: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle f\left(x_{1},\dots,x_{n}\right)=\sum_{i,j}^{n}x_{i}a_{ij}x_{j}}
De forma que podemos representá-la matricialmente como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f\left(\boldsymbol{x}\right)=\boldsymbol{x}^{T}P\boldsymbol{x}}
Onde: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{x}=\left(x_{1},\dots,x_{n}\right),\qquad P=\left(\begin{array}{ccc} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots\\ a_{n1} & \dots & a_{nn} \end{array}\right)}
Além disso, qualquer forma quadrática pode ser representada por uma matriz simétrica[1], substituindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle a_{ij}^{s}=a_{ji}^{s}=\frac{a_{ji}+a_{ij}}{2}} para quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle a_{ij}\neq a_{ji}} . Ou de maneira genérica:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^{s}=\frac{P+P^{T}}{2}}
Então só precisamos nos preocupar com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle P} para classificar a função quadrática. Se os menores principais líderes são maiores que zero, temos um positivo definido. Isto é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|D_{1}\right|=\left|a_{11}\right|>0,\left|D_{2}\right|=\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|>0,\dots,\left|D_{n}\right|=\left|\begin{array}{ccc} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots\\ a_{n1} & \dots & a_{nn} \end{array}\right|>0}
Lembrando que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|M\right|} denota o determinante da matriz Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle M} . Para um positivo semidefinido, precisamos levar em conta todos os menores. Isto é, quando a matriz que obtemos não corresponde necessariamente ao quadrante superior esquerdo da matriz. Neste caso se todos os menores principais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D_{j}} são maiores ou iguais a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0} (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D_{j}\geq0} ) temos uma função semidefinida positiva.
Já para o negativo definido, temos a seguinte condição para os menores principais líderes:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|D_{1}\right|<0,\left|D_{2}\right|>0,\left|D_{3}\right|<0,\dots}
Ou seja uma alternância de sinal começando com negativo. Para o negativo semidefinido temos algo análogo porém com todas as matrizes menores, as ímpares são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \leq0} e as pares Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \geq0} . Uma forma mais fácil de classificarmos a matriz é olhando para seus autovalores. Se todos os autovalores da matriz são:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{i}>0} : positivo definido
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{i}<0} : negativo definido
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{i}\geq0} : positivo semidefinido
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \lambda_{i}\leq0} : negativo semidefinido
Retornando ao sistema não linear:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\boldsymbol{x}}=\boldsymbol{f}\left(\boldsymbol{x}\left(t\right),\boldsymbol{u}_{0}\right)}
Considerando um sistema autônomo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\boldsymbol{x}}=\boldsymbol{f}\left(\boldsymbol{x}\right)}
Pelo segundo critério de Lyapunov, se na vizinhança Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W} de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}_{0}} existe uma função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right):W\rightarrow\mathcal{R}} positiva definida e:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\leq0} , então o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}_{0}} é estável;
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}}
for negativo definido, o ponto é assintoticamente estável;
- Ainda há um ’refinamento’ para determinar estabilidade assintótica quando Lyapunov garante apena estabilidade (critério de La Salle-Krasowski).
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}}
for positivo definido, o ponto é instável.
- Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}_{0}} for um ponto de acumulação para um conjunto de pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}\in W} em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)>0} , o critério também pode ser usado se a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)} não for positiva definida em todo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W} .
Aqui talvez vale a pena fazer uma breve discussão sobre o que é ser um ponto de acumulação e alguns conceitos relacionado.
- Ponto de acumulação: Um ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}} é um ponto de acumulação do conjunto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}\subseteq W} se todas as suas vizinhanças abertas contém ao menos um ponto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} distinto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}} .
- Vizinhança aberta: a vizinhança aberta de um ponto é todo conjunto aberto que contém o ponto.
- Conjunto aberto:
- Uma bola aberta é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle K\left(x,r\right)=\left\{ y\in R^{n}:d\left(x,y\right)<r\right\}} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle d\left(x,y\right)} é a distância entre dois pontos. Então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle K\left(x,r\right)} é uma bola aberta centrada em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x} com raio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r} .
- Um conjunto aberto é uma união de bolas abertas. Ou seja um conjunto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}\subseteq \mathcal{R}^{n}} é um conjunto aberto se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(\forall x\in W^{+}\right)\left(\exists r>0\right)K\left(x,r\right)\subseteq W^{+}} , em palavras, para todo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}} que pertence a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} , existe um raio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r} maior que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0} em que temos uma bola aberta centrada em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x} com raio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r} que é um subconjunto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} .
- Conjunto aberto é uma generalização de intervalos abertos.
- Como exemplo de conjunto aberto, podemos citar o interior de um disco com a fronteira delimitada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x^{2}+y^{2}=r^{2}} . Este conjunto de pontos que satisfazem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x^{2}+y^{2}<r^{2}} é um conjunto aberto.
Para compreender melhor o critério, devemos lembrar que o segundo método de Lyapunov é uma generalização baseada em dois princípios físicos básicos:
- Um sistema conservativo é estável somente se sua energia potencial tem um mínimo local no ponto de equilíbrio;
- A energia total de um sistema conservativo é constante durante a evolução do sistema.
Então podemos voltar a física clássica e encarar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x},t\right)} como uma energia potencial, logo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\left(\boldsymbol{x},t\right)} é a variação da energia potencial ao longo do tempo. Ou melhor, se considerarmos um sistema mecânico em que a energia é total dada pela soma da potencial e a cinética, então se tivermos uma energia cinética inicial nula, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}_0,t_0\right)} representa a energia inicial total do sistema.
Podemos pensar em um poço potencial em 2 dimensões, potencial em formato de uma "bacia" por exemplo, caso o sistema seja conservativo (não retiramos nem acrescentarmos energia ao sistema), se largarmos uma bolinha em um ponto qualquer, ela ficará oscilando oscilando em torno da origem, que é um ponto de equilíbrio estável. Se tivermos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(x,y\right)=x^{2}+y^{2}} , podemos ver facilmente que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{0}\right)=0} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)>0} se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x} \neq \boldsymbol{0}} . Nesse caso a força que atuando sobre a bolinha é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{F}=-\nabla V=-2\left(x,y\right)} . Então analisando por exemplo sobre o eixo x (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0} ), se estiver no sentido positivo (negativo) de x, vai sentir uma força em direção a origem, isto é
negativa (positiva), uma força restaurativa, neste caso também temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\left(x,y\right)=0} . Para uma dimensão temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{x}+\frac{2}{m}x=0} , esta é uma equação da onda e tem como solução uma soma de senos e cossenos, ou seja periódica.
Porém se o sistema estiver perdendo energia, então o estado do sistema vai se aproximar do ponto de equilíbrio uma vez que ele seja um mínimo local. Nesta situação temos um ponto de equilíbrio assintoticamente estável. No caso da bolinha poderia ser representado por exemplo pelo atrito que retira energia do sistema, porém ele retira energia cinética. Vamos usar uma analogia diferente: um sistema massa mola em uma dimensão. Neste caso temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=-kx} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(x\right)=\frac{kx^{2}}{2}} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} é a constante da mola, onde quanto maior a constante, maior a força restauradora e maior a energia potencial. Se consideramos que a mola "cansa" com o tempo, e utilizarmos por exemplo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=\frac{2}{t}} , ficamos com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=-\frac{2x}{t}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(x,t\right)=\frac{x^{2}}{t}} . Podemos ver que ainda temos as condições satisfeitas para a função de Lyapunov ( Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(0,t\right)=0} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(x,t\right)>0} se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left(x,t\right) \neq \boldsymbol{0}} ), porém agora temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\left(x,t\right)<0} . Isso acontece pois o sistema está perdendo energia na forma de uma diminuição na energia potencial do sistema como um todo. Observando quando a bolinha se desloca entre um extremo e o ponto de origem, temos que a energia potencial está parte sendo convertida em energia cinética, mas parte está simplesmente sendo retirada do sistema. A cada oscilação o ponto extremo ponto possui uma energia cada vez menor e consequentemente uma força restaurativa também cada vez menor. Até que a massa atinge o equilíbrio. O sistema físico em questão, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{x}+\left(\frac{2}{mt}\right)x=0} , temo como solução funções de Bessel. Estas funções tem comportamento similares a funções senos (ou cossenos) amortecidas[2].
Antes de avançar para a discussão da instabilidade, vamos lembrar que quando queremos demonstrar que um ponto de equilíbrio é estável, precisamos analisar toda a vizinhança do ponto de equilíbrio, pois precisamos garantir que em qualquer estado inicial próximo ao ponto de equilíbrio, o sistema não se afaste do mesmo. Porém para o critério de instabilidade, não temos a mesma exigência, uma vez que se ele se afastar em um eixo, é o suficiente para ser classificado como um ponto instável. E agora também temos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\left(x,y\right)>0} , isto é, o sistema está recebendo energia, o que permite que se afaste do ponto de equilíbrio. Fisicamente isso pode ser, por exemplo, um sistema que aumente a energia potencial de acordo com a temperatura, e colocamos o sistema sobre o fogo.
Para ilustrar esse último exemplo, vamos utilizar um potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(x,y,t\right)=t\left(x^{2}-y^{2}\right)} , podemos notar que se não fosse explicitamente dependente do tempo, teríamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{V}\left(x,t\right)=0} , porém o potencial não é positivo definido na vizinhança da origem, dessa forma, não podemos garantir a estabilidade. Temos então novamente satisfeito Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(0,0,t\right)=0} porém agora temos apenas um subconjunto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle W^+} de pontos em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(0,0,t\right)>0} , especificamente quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|x\right|>\left|y\right|} . E a variação de energia neste ponto é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{V}\left(x,y,t\right)>0} , então temos um ponto de instabilidade. Podemos observar ainda que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(0,0\right)} é um ponto de sela para a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,y)=x^{2}-y^{2}} , para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0} se reduz a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=x^{2}} , então se reduzíssemos o problema a uma dimensão sobre o eixo x, o potencial poderia ser classificado como uma função positiva definida. Resolvendo o sistema físico sobre em uma dimensão, temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{x}+\left(\frac{2t}{m}\right)x=0} , a solução deste sistema é escrita em termos de funções de Airy, e tende a infinito quando a variável independente tende a infinito.
Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)} uma função de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}\left(t\right)} , então temos:Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{V}\left(\boldsymbol{x}\right) & =\frac{\partial V}{\partial x_{1}}\frac{\partial x_{1}}{\partial t}+\dots+\frac{\partial V}{\partial x_{n}}\frac{\partial x_{n}}{\partial t}\\ & =\left[\frac{\partial V}{\partial x_{1}},\dots,\frac{\partial V}{\partial x_{n}}\right]\cdot\left[\dot{x}_{1},\dots,\dot{x}_{n}\right]\end{align}}
E como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \nabla V=\left[\frac{\partial V}{\partial x_{1}},\dots,\frac{\partial V}{\partial x_{n}}\right]} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{\boldsymbol{x}}=\left[\dot{x}_{1},\dots,\dot{x}_{n}\right]} , reescrevemos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{V}\left(\boldsymbol{x}\right)=\left[\nabla V\right]\cdot\left[\boldsymbol{f}\left(\boldsymbol{x}\right)\right]}
Como exemplo, se temos o seguinte sistema:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{x}_{1} & =+x_{1}-x_{1}x_{2}\\ \dot{x}_{2} & =-x_{2}+x_{1}x_{2}\end{align}}
Um ponto de equilíbrio é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}_{0}=0} . Considerando a seguinte função de Lyapunov:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(\boldsymbol{x}\right)=x_{1}^{2}-x_{2}^{2}}
Temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}_{0}\right)=0} . além disso temos um conjunto de pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle V\left(\boldsymbol{x}\right)>0} quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|x_{1}\right|>\left|x_{2}\right|} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \boldsymbol{x}_{0}} é um ponto de acumulação de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} . Então calculando a derivada da função de Lyapunov:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{V}\left(\boldsymbol{x}\right) & =\left[\nabla V\right]\cdot\left[\boldsymbol{f}\left(\boldsymbol{x}\right)\right]\\ & =\left(2x_{1},-2x_{2}\right)\left(+x_{1}-x_{1}x_{2},-x_{2}+x_{1}x_{2}\right)\\ & =2x_{1}^{2}-2x_{1}^{2}x_{2}+2x_{2}^{2}-2x_{1}x_{2}^{2}\\ & =2x_{1}^{2}\left(1-x_{2}\right)+2x_{2}^{2}\left(1-x_{1}\right)\end{align}}
Como estamos avaliando a região Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} próxima ao ponto do equilíbrio, que neste caso está localizado na origem, podemos assumir que há uma região em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{1},x_{2}<1} e logo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \dot{V}\left(\boldsymbol{x}\right)>0} é positivo definido em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle W^{+}} . Sendo assim, temos um ponto de instabilidade.
Principais materiais utilizados
- Dinâmica e Sistemas Dinâmicos (Jaime E. Villate, Universidade do Porto)
- Lyapunov stability (Christopher J. Damaren, Universidade de Toronto)
- Sketching Non-Linear Systems (Instituto de Tecnologia de Massachusetts)
- Stability Analysis of Nonlinear Systems (Roberto Zanasi, Universidade de Módena e Reggio Emília)
Citações
- ↑ Quadratic Forms (Tornike Kadeishvili, Universidade Estatal de Tbilisi)
- ↑ Bessel Function and Damped Simple Harmonic Motion (Masoud Asadi-Zeydabadi, Revista de Física e Matemática Aplicada)
Anterior: Linearização de sistemas de equações não lineares | Índice: Ecologia | Próximo: Introdução à equações diferenciais com atraso





