Grupo - Ising 2D: mudanças entre as edições
| (94 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo: Ânderson Rosa, Caetano Pires e Lucas Doria.''' | '''Grupo: Ânderson Rosa, Caetano Pires e Lucas Doria.''' | ||
O objetivo deste trabalho é estudar o comportamento de um sistema de Ising spins a partir do método de Monte Carlo. O problema do ferromagnetismo em um material foi abordado utilizando o algoritmo de metrópolis, considerando que o sistema interagia com um reservatório térmico externo. Várias propriedades do sistema foram investigadas, tais como a magnetização total, a energia por spin, o calor específico e a suscetibilidade magnética do sistema. | |||
== | == Modelo de Ising == | ||
- | A denominação "modelo de Ising" é utilizada para tratar um sistema de spins de Ising <math>s={s_1,s_2,..s_i,...s_N}</math> que podem assumir valor <math>+1</math> e <math>-1</math>, respectivamente "up" e "down", onde <math>N</math> é a quantidade máxima de spins, ao qual se acopla uma dinâmica que lhe proporciona relaxamento para um estado de equilíbrio. A evolução desse sistema de spins é descrito por uma dinâmica que possui as propriedades do processo de Markov de balanceamento detalhado e ergocidade, garantindo ao sistema que sua evolução o leva a estados estacionários de equilibrio descritos pela distribuição de Gibbs relacionada à hamiltoniada de Ising. | ||
- | O modelo de Ising 2D tratado neste trabalho possui seus spins organizados em uma rede quadrada bidimensional de tamanho <math>N=L\times L</math> com vizinhança de Von Newmann e condições de contorno periódicas. A energia desse sistema é descrita pela equação <ref name=giordano>N. J. Giordano, "Computational Physics". Department of Physics, Purdue University. Upper Saddle River, New Jersey. Prentice-Hall, 1997.</ref> | ||
- | <math>E = -J \sum_{<ij>} s_i s_j - \mu H \sum_i s_i,</math> | ||
onde <math>J</math> é a taxa de transição, <math>H</math> representa o campo magnético externo e <math>\mu</math> o momento magnético associado com cada spin. O primeiro somatório é sobre todas as vizinhanças de spins e o segundo sobre todos os spins. Neste trabalho, particularmente, escolhemos <math>J=1</math> para favorecer menores energias em spins apontados para cima (<math>s=1</math>), <math>\mu = 1 </math> e <math>0\le H</math> | |||
A magnetização desse sistema é dada pela soma de todos os valores de spins: | |||
<math>M = \sum_{i=1}^N <s_i> </math>. | |||
Utilizando a abordagem da mecânica estatística, conforme descrito por Gibbs (1902), podemos estimar valores médios de propriedades macroscópicas de um sistema termodinâmico, como energia ou magnetização, a partir de uma amostragem de Boltzmann relativa ao valor da propriedade sobre todos os estados do sistema. Sendo assim, podemos estimar o valor energia do nosso sistema em estado de equilibro termodinâmico como sendo | |||
<math><E> = \frac{1}{Z}\sum_{\nu}E_{\nu} e^{-E{\nu}/kT}</math> | |||
<math> | onde Z é a função partição <math>Z = \sum_{\nu} e^{-E{\nu}/kT} </math>, <math> E_{\nu}</math> é a energia do sistema no estado <math>\nu</math>, <math>T</math> é a temperatura de um reservatório em contato com o sistema e <math>k</math> é a constante de Boltzmann, escolhida nesse trabalho como tendo valor unitário. O mesmo serve para a magnetização: | ||
<math><M> = \frac{1}{Z}\sum_{\nu}|M_{\nu}| e^{-E{\nu}/kT}</math>, onde <math><M></math> é medido sobre o módulo da <math>M_{\nu}</math>, que é a magnetização no estado <math>\nu</math>. | |||
Outra medida relevante é a suscetibilidade magnética do sistema, dada por | |||
<math>\chi = \frac{<M^2> - <M>^2}{Nk_BT},</math> | |||
<math> | onde <math>N</math> é o número total de spins <math>(L^2)</math>, <math><M^2></math> e <math><M></math> são, respectivamente, a média quadrática da magnetização e média da magnetização durante a simulação. | ||
Por fim, temos a medida do calor específico por spin do sistema, dada por | |||
<math>c_{spin} = \frac{<E^2> - <E>^2}{Nk_B^2T^2},</math> | |||
<math> | onde <math><E^2></math> e <math><E></math> são, respectivamente, a média quadrática da energia do sistema e média da energia durante a simulação. | ||
== O Método de Monte Carlo == | |||
<math>< | === Algorítmo de Metrópolis === | ||
Para o método de Monte Carlo responsável por gerar configurações do sistema, utilizaremos o Algorítmo de Metropolis. O algoritmo funcionará escolhendo repetidamente um novo estado <math>\nu</math> e aceitando ou rejeitando o estado de acordo com uma probabilidade de aceitação <math>A(\mu \rightarrow \nu)</math> de transitar de um estado antigo <math>\mu</math> para o novo estado <math>\nu</math>. O algoritmo que iremos descrever utiliza a dinâmica de inversão única de spins, onde apenas um spin será invertido aleatoriamente para termos um novo estado a ser testado. | |||
É válido notar que a dinâmica de inversão única de spins não é o que caracteriza o método de Metropolis, pois ainda poderíamos ter esse método ao utilizarmos uma dinâmica com mais spins sendo invertidos simultaneamente. | |||
Temos que a condição de balanceamento detalhado é dada por <ref>M. E. J. Newman, G. T. Barkema, "Monte Carlo Methods in Statistical Physics". Oxford University Press Inc., New York, 1999.</ref>: | |||
<math>\frac{A(\mu \rightarrow \nu)}{A(\nu \rightarrow \mu)} = e^{-\frac{\Delta E}{k_BT}}, \qquad (3)</math> | |||
onde <math>\Delta E = E_\nu - E_\mu</math>. | |||
Vamos supor que tenhamos os estados <math>\mu</math> e <math>\nu</math> e que temos a relação de energias: <math>E_\mu < E_\nu</math>. Então, a maior das duas chances de aceitação é <math>A(\nu \rightarrow \mu)</math>, portanto iremos igualar essa probabilidade a 1. | |||
Para que <math>(3)</math> seja respeitada, iremos definir o valor de <math>A(\mu \rightarrow \nu)</math> como <math>e^{-\frac{\Delta E}{k_BT}}</math>. Temos, assim, o algoritmo de Metropolis: | |||
<math>A(\mu \rightarrow \nu) = \begin{cases} | |||
e^{-\frac{\Delta E}{k_BT}}, \qquad \text{se } \Delta E > 0\\\\ | |||
1, \qquad \qquad \text{caso contrario}. | |||
\end{cases}</math> | |||
Dessa forma, sempre que tivermos um estado cuja energia seja menor do que a do estado atual, iremos aceitar a transição, mas se a energia for maior, teremos uma pequena probabilidade de trocarmos de estado. | |||
Para que o | === Implementação === | ||
Para a implementação do método, utilizaremos uma matriz <math>L\times L</math> com condições de contorno periódicas, i.e., faremos com que os vizinhos de uma fronteira da matriz sejam os spins na outra fronteira correspondente. Isso irá garantir que todos os spins tenham o mesmo número de vizinhos e a mesma geometria local. Cada spin da matriz poderá assumir apenas os valores de +1 e -1, representando a magnetização desse spin. | |||
Para o estado inicial do sistema, podemos escolher entre duas opções muito utilizadas: ou determinamos <math>T=0</math> e todos os spins, portanto, estarão alinhados na mesma direção, ou assumimos <math>T=\infty</math>, o que fará com que tenhamos uma configuração aproximadamente aleatória, garantido uma magnetização média do sistema de aproximadamente 0. | |||
Uma boa estratégia para otimizarmos a simulação é calcular a energia total do sistema no estado inicial utilizando a equação <math>(1)</math> e durante a dinâmica da simulação calcularmos apenas <math>\Delta E</math>, atualizando a nova energia do sistema com <math>E_\nu = E_\mu + \Delta E</math>. | |||
Para obtermos um novo estado, escolhemos aleatoriamente um spin e calculamos a variação de energia ao invertemos ele. Da equação <math>(1)</math>, temos que só um spin <math>(s_k)</math> irá mudar de estado; logo, apenas seus vizinhos serão afetados. Temos que, para qualquer valor de <math>s_k</math>, <math>s_k^\nu - s_k^\mu = -2s_k^\mu</math>. Utilizando isso e fazendo a diferença entre as energias, podemos escrever | |||
= | <math>\Delta E = 2s_k^\mu(J\displaystyle \sum_j s_{j} + H)</math> | ||
onde o somatório se dá nos vizinhos de <math>s_k</math> e, como os vizinhos de <math>s_k</math> não mudam de estado, <math>s_j^\mu = s_j^\nu</math> para qualquer <math>j</math>. | |||
De forma similar ao que foi feito para a energia, uma boa estratégia de otimização para a medida da magnetização é calcular a magnetização total do sistema no estado inicial e então somar <math>\Delta M</math> sempre que o sistema aceitar a mudança de estado. Sendo que para qualquer <math>s_k</math> temos <math>\Delta M = s_k^\nu - s_k^\mu = 2s_k^\nu</math>, temos que | |||
<math>M_\nu = M_\mu + 2s_k^\nu.</math> | |||
Antes de começar o registro das medidas de magnetização e energia do sistema é interessante dar um tempo de equilíbrio para o sistema, ou seja, deixar a simulação ocorrer durante um determinado tempo para eliminar problemas transientes do sistema e o sistema tender a um estado de equilíbrio. Após esse tempo, inicia-se o registro. Os valores do calor específico por spin e da susceptibilidade magnética são feitos após o fim da dinâmica de Monte Carlo. | |||
Durante todo o processo de simulação que fizemos, utilizamos medidas de temperatura em unidades de energia. Dessa forma, temos <math>k_B = 1</math>. Além disso, também utilizamos <math>J=1</math>. Também escolhemos medir o tempo de simulação em passos de Monte Carlo (Monte Carlo steps, ou apenas MCS), que representa o fato de que todos os spins do sistema receberam a chance de inverterem de estado. Em outras palavras, em um sistema com N spins, já ocorreram N seleções aleatórias de spins para tentar a mudança de estado. A partir disso, podemos utilizar o método de amostragem por importância para medir as médias da energia e da magnetização, além das médias da magnetização quadrada e da energia quadrada: | |||
<math><E> = \frac{1}{MCS}\sum_{\nu}E_{\nu}</math> | |||
<math><E^2> = \frac{1}{MCS}\sum_{\nu}E_{\nu}^2</math> | |||
<math><M> = \frac{1}{MCS}\sum_{\nu}|M_{\nu}|</math> | |||
<math> | <math><M^2> = \frac{1}{MCS}\sum_{\nu}M_{\nu}^2</math> | ||
</math> | |||
onde <math> | onde <math>MCS</math> é a quantidade de passos de Monte Carlo dadas. | ||
== Resultados == | |||
Para analisarmos os resultados obtidos pelo método de Metropolis, realizamos diversas medidas em sistemas com dimensões <math>20\times20</math>, <math>36\times36</math> e <math>48\times48</math>. Utilizamos para todas as medidas um tempo de equilíbrio de <math>10^5</math> Monte Carlo Steps e fizemos <math>10^6</math> medidas. | |||
<math> | Primeiramente, fizemos medidas para sistemas sem campo magnético, ou seja, <math>H=0</math>. Com isso, montamos histogramas da magnetização por spins e da energia por spins do sistema para cada um dos 3 casos em três diferentes temperaturas: | ||
</math> | |||
== | [[Arquivo:Hist20.png|frameless|upright=5]] | ||
[[Arquivo:Hist36.png|frameless|upright=5]] | |||
[[Arquivo:Hist48.png|frameless|upright=5]] | |||
Imediatamente é possível notar que, para todas as temperaturas, quanto maior o número de spins, menor é a variância da energia, com as larguras das gaussianas ficando menores. Para a magnetização, para temperaturas menores que a temperatura crítica <math>T_c \approx 2.269</math> e tempos de simulação suficientemente longos, era esperado que tivéssemos duas gaussianas simétricas e de mesma altura, já que os spins estão livres para assumirem valores de +1 e -1. Esse resultado é facilmente observado para <math>T=2.2</math> no sistema 20x20, mas para os sistemas 36x36 e 48x48 as gaussianas possuem alturas diferentes. Esses resultados são indicativos do efeito de redes maiores, onde temos que quanto maior a rede, menor a probabilidade de haver mudança de magnetização do sistema, exigindo tempos de simulação cada vez maiores. Esse efeito pode ser observado ao compararmos as séries temporais da magnetização dos três sistemas: | |||
[[Arquivo:Séries.png|thumb|upright=5|none|alt=Alt text|Séries temporais da magnetização para os sistemas 20x20 (esquerda), 36x36 (centro) e 48x48 (direita).]] | |||
<math> | Como podemos ver pelas séries temporais, no mesmo período de tempo, o sistema 20x20 troca de estado diversas vezes, enquanto o sistema 36x36 troca apenas uma vez para o estado -1 e o sistema 48x48 não troca nenhuma vez para o estado -1. | ||
M = | Além disso, pelos histogramas, é possível notar que quanto maior a temperatura em relação à temperatura crítica, mais a magnetização do sistema tende a zero, ou seja, as duas gaussianas vão se somando em <math>M=0</math>, resultado da transição de fase do ferromagnetismo para o paramagnetismo. | ||
</math> | |||
[[Arquivo:MeExT.png|thumb|upright=5|none|alt=Alt text|Energia (esquerda) e magnetização (direita) em função da temperatura para diferentes tamanhos de rede. <math>T_c \approx 2.269</math>.]] | |||
Fazendo um gráfico para a energia em função da temperatura e da magnetização em função da temperatura para cada um dos sistemas, podemos ver que a energia aumenta com o aumento da temperatura, enquanto a magnetização decresce com o aumento da temperatura. Também é possível notar que em ambos os gráficos os resultados para os três tamanhos de sistemas são aproximadamente iguais até a a temperatura aproximar-se da temperatura crítica. Conforme a temperatura se aproxima da transição de fase, os resultados deixam de ser aproximadamente iguais, pois a energia passa a ser maior para redes maiores e voltam a tornarem-se similares após <math>T=2.5</math>. Para a magnetização, ao se aproximar da transição de fase, a magnetização decresce muito mais rapidamente em redes maiores, com os resultados tendendo a zero com o aumento da temperatura. | |||
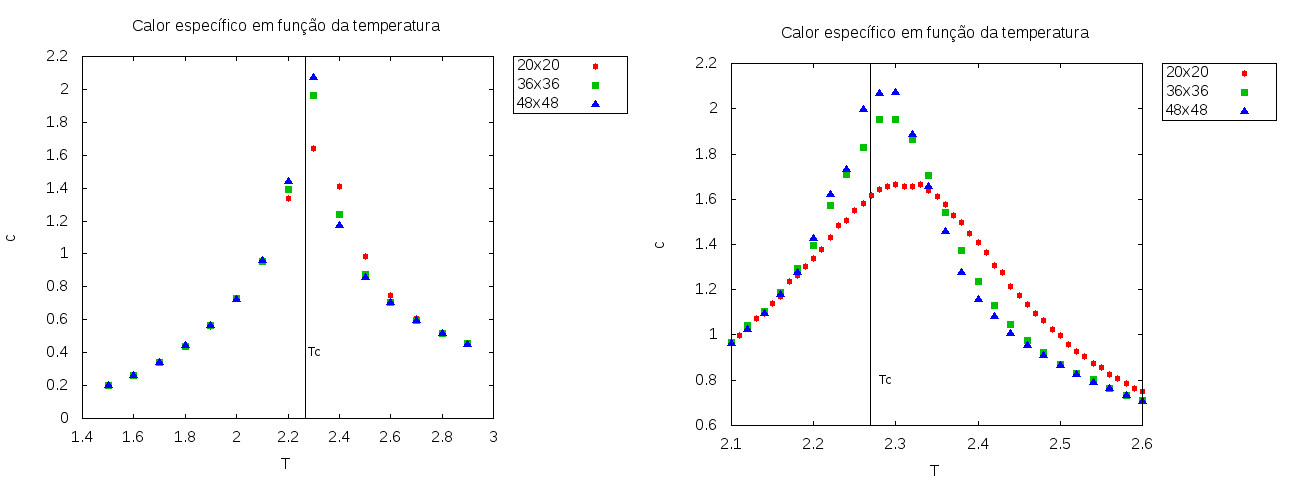
[[Arquivo:SeXxT.png|thumb|upright=5|none|alt=Alt text|Calor específico em função da temperatura para diferentes tamanhos de rede. À esquerda um gráfico para uma faixa grande de temperaturas e à direita um gráfico detalhado próximo da temperatura crítica. <math>T_c \approx 2.269</math>.]] | |||
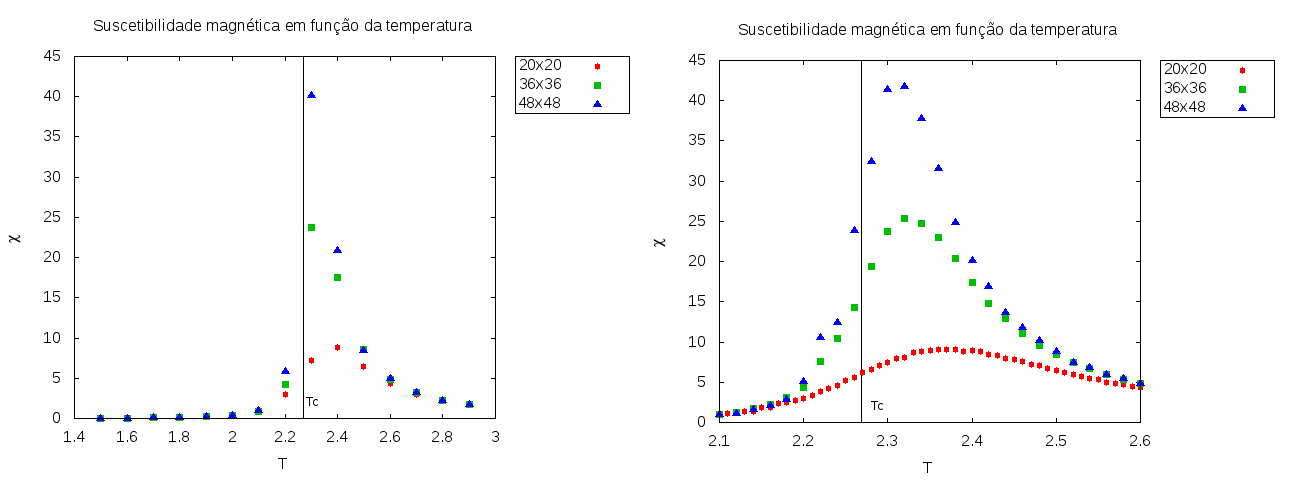
[[Arquivo:XxT.png|thumb|upright=5|none|alt=Alt text|Suscetibilidade magnética em função da temperatura para diferentes tamanhos de rede. À esquerda um gráfico para uma faixa grande de temperaturas e à direita um gráfico detalhado próximo da temperatura crítica. <math>T_c \approx 2.269</math>.]] | |||
<math> | Analisando os gráficos da suscetibilidade magnética e do calor específico em função da temperatura, podemos perceber que tanto a suscetibilidade magnética quanto o calor específico aumentam quando a temperatura se aproxima da temperatura crítica, com ambos os gráficos possuindo curvas que se tornam mais estreitas próximo de <math>T_c</math>, com os gráficos sendo mais estreitos em redes maiores. Também podemos ver que ambos os gráficos começam a decair um pouco após a temperatura crítica. Isso significa que as variâncias da energia e da magnetização aumentam consideravelmente com a transição de fase do sistema, implicando no aumento da suscetibilidade magnética e do calor específico ao redor da temperatura crítica. É possível perceber que esse efeito é maior em redes maiores, onde há uma grande diferença entre os valores das redes de diferentes tamanhos. No gráfico com a faixa de temperatura maior, podemos ver que para temperaturas menores que T = 2.1 e maiores que T = 2.8 tanto a suscetibilidade magnética quanto o calor específico possuem valores aproximadamente iguais para todos os tamanhos de rede. | ||
=== Um resultado de redes grandes === | |||
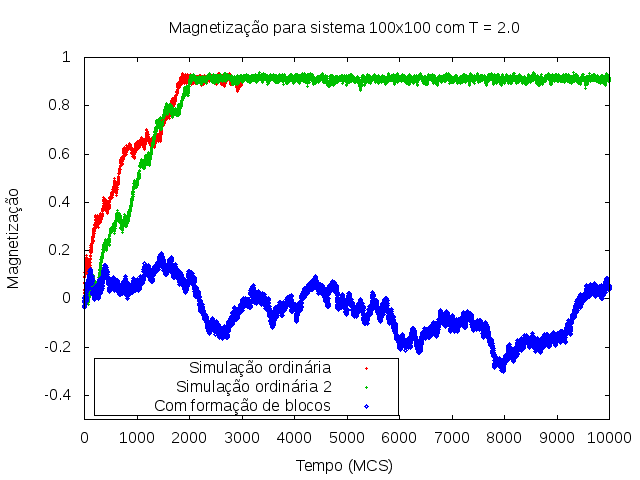
Algo que pode resultar de simulações com redes grandes é o aparecimento de blocos de spins. Em uma rede suficientemente grande, pode ocorrer o aparecimento de aglomerados (clusters) de spins de determinada magnetização e esses aglomerados podem acabar crescendo até que se formem blocos de spins com uma direção que dão um resultado não tão esperado para o sistema. Um exemplo pode ser visto ao simularmos um sistema <math>100\times100</math> com temperatura <math>T=2.0</math>. Nessas condições, o sistema tende a ficar aproximadamente estável com magnetização aproximadamente +1 ou -1. Contudo, eventualmente pode ocorrer de uma simulação acabar com uma magnetização variando próximo de zero, como é possível ver na série temporal: | |||
<math> | [[Arquivo:Serie100.png|thumb|upright=3|none|alt=Alt text|Série temporal da magnetização. É possível notar que regularmente a série converge rapidamente para um estado com magnetização +1 (note que poderia também convergir para -1), mas há a possibilidade de ficar oscilando próximo de <math>M=0</math>.]] | ||
</math> | |||
Ao olharmos um snapshot do estado de ambos os sistemas conseguimos entender o que está acontecendo: | |||
[[Arquivo:Snapshots.png|thumb|upright=4|none|alt=Alt text|Snapshot de uma simulação ordinária (esquerda) de um sistema 100x100 a uma temperatura de T=2.0 que convergiu para M = +1 e snapshot de um sistema (direita) onde ocorreu o aparecimento de blocos de spins. Pontos pretos são spins com magnetização +1 e pontos brancos são spins com magnetização -1. Ambas snapshots tiradas após <math>10^4</math> Monte Carlo steps.]] | |||
</math> | |||
No snapshot da simulação ordinária conseguimos ver que a maior parte dos spins estão com magnetização +1, o que está de acordo com a série temporal. Já no outro snapshot, temos a formação de um bloco de spins com magnetização -1 ocupando uma faixa vertical completa do sistema. Esse estado da rede faz com que spins que sejam invertidos dentro de um dos blocos influenciem muito pouco a magnetização do sistema e os spins das fronteiras entre os blocos que forem invertidos acabam apenas sendo invertidos novamente, fazendo com que a magnetização total do sistema oscile, mas se mantenha sempre próxima do mesmo valor. Para ilustrarmos esse efeito, temos uma animação para cada uma das evoluções: sem a formação de blocos e com formação de blocos. | |||
<math>\ | [[Arquivo:Sembloco.gif|thumb|upright=4|none|alt=Alt text|Animação do sistema convergindo para magnetização +1 correspondente à série temporal "Simulação ordinária" no gráfico das séries temporais. Animação feita até <math>3\times10^3</math> Monte Carlo steps. Pontos pretos são spins com magnetização +1 e pontos brancos são spins com magnetização -1.]] | ||
[[Arquivo:Formarbloco.gif|thumb|upright=4|none|alt=Alt text|Animação do sistema com formação de um bloco vertical de spins com magnetização +1. Animação feita até <math>3\times10^3</math> Monte Carlo steps. Pontos pretos são spins com magnetização +1 e pontos brancos são spins com magnetização -1.]] | |||
Para que | === Simulação com campo magnético === | ||
Para fazermos a simulação do modelo de Ising com campo magnético não nulo e termos resultados interessantes de serem observados, precisamos de duas características: primeiro, precisamos que o campo magnético seja pequeno para que possamos fazer observações, pois para campos magnéticos grandes os spins irão se alinhar rapidamente à direção do campo e, portanto, será pouco provável a mudança de estado do sistema. A segunda característica que precisamos é a de que a rede seja pequena, pois quanto maior a rede, menos provável é o sistema mudar de estado em tempos de simulação viáveis, assim como foi visto nos resultados sem campo magnético. | |||
Utilizando uma rede 20x20, fizemos histogramas para diferentes temperaturas para dois diferentes campos magnéticos: | |||
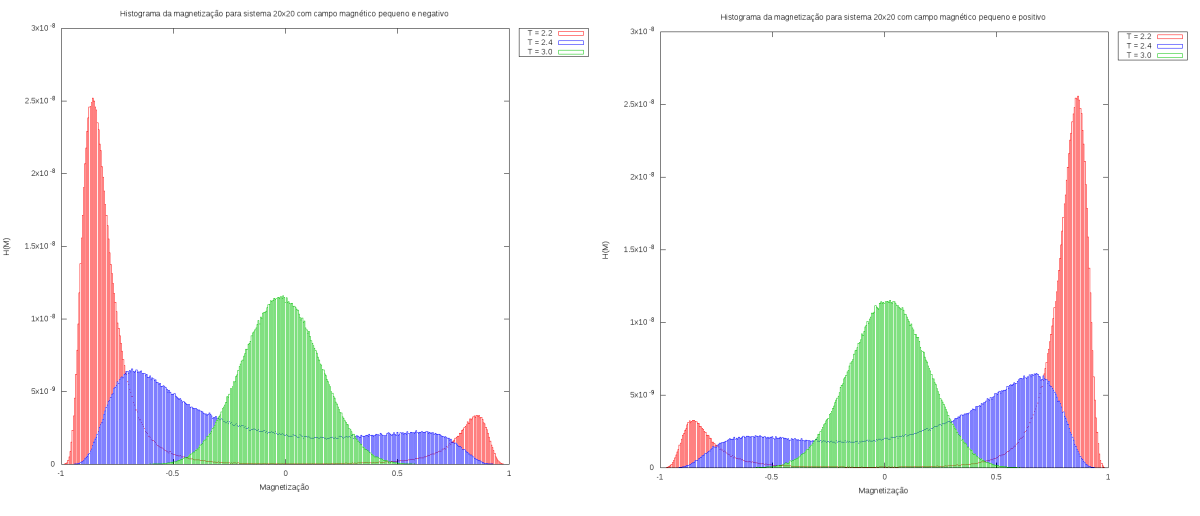
<math> | [[Arquivo:Histogramas com campo.png|thumb|upright=4|none|alt=Alt text|Histogramas da magnetização de uma rede 20x20 sob efeito de um campo magnético. À esquerda temos um campo magnético atuante <math>H = -0.005</math> e à direita temos um campo magnético <math>H = 0.005</math>.]] | ||
e | |||
Podemos observar que para a temperatura inferior a <math>T_c</math>, temos a formação de uma gaussiana muito maior do que a outra, com a maior gaussiana sendo a que tem a magnetização alinhada com a direção do campo magnético exercendo influencia na rede. Ao utilizarmos temperaturas maiores que a temperatura crítica, vemos a magnetização aumentar ao redor de M = 0, até que em T = 3.0 temos apenas uma gaussiana centrada em M = 0, o que está de acordo com a transição de fase do sistema. | |||
Caso não tivéssemos respeitado uma das duas características citadas anteriormente para a simulação de Ising com campo magnético, a maior diferença estaria no sistema com temperatura inferior à temperatura crítica, pois teríamos a formação de apenas uma gaussiana e ela estaria alinhada à direção do campo magnético aplicado ao sistema. | |||
== | == Conclusões e Observações == | ||
O modelo de Ising estudado neste trabalho é um modelo de spin extremamente simples. Outros modelos podem ser estudados. Por exemplo, podemos considerar os spins como sendo vetores de comprimento constante mas que tenham movimento de rotação em um plano[https://en.wikipedia.org/wiki/Classical_XY_model], ou até mesmo considerar vetores em três dimensões[https://en.wikipedia.org/wiki/Classical_Heisenberg_model]. Além disso, o alcance das interações entre os spins do sistema pode ser incrementada para os segundos, terceiros ou até mais distantes vizinhos mais próximos de um spin. Todos esses modelos têm sido estudados extensivamente. Apesar disso, o modelo simples em 2D com spins +1 e -1 estudado ainda representa bem as propriedades do sistema, principalmente o fenômeno de transição de fase. | |||
== Programas utilizados em linguagem C == | |||
[[Séries temporais e histogramas sem campo magnético]] | |||
[[Magnetização e energia em função da temperatura]] | |||
[[Suscetibilidade magnética e calor específico]] | |||
[[Animação da evolução do estado do sistema]] | |||
[[Série temporal e histograma da magnetização com campo magnético]] | |||
== Referências == | |||
<references/> | |||
== Bibliografias == | |||
Tânia Tomé, Mário J. de Oliveira, "Stochastic Dynamics and Irreversibility". Universidade de São Paulo, São Paulo, Brasil. 2015. | |||
Edição atual tal como às 18h35min de 26 de janeiro de 2018
Grupo: Ânderson Rosa, Caetano Pires e Lucas Doria.
O objetivo deste trabalho é estudar o comportamento de um sistema de Ising spins a partir do método de Monte Carlo. O problema do ferromagnetismo em um material foi abordado utilizando o algoritmo de metrópolis, considerando que o sistema interagia com um reservatório térmico externo. Várias propriedades do sistema foram investigadas, tais como a magnetização total, a energia por spin, o calor específico e a suscetibilidade magnética do sistema.
Modelo de Ising
A denominação "modelo de Ising" é utilizada para tratar um sistema de spins de Ising que podem assumir valor e , respectivamente "up" e "down", onde é a quantidade máxima de spins, ao qual se acopla uma dinâmica que lhe proporciona relaxamento para um estado de equilíbrio. A evolução desse sistema de spins é descrito por uma dinâmica que possui as propriedades do processo de Markov de balanceamento detalhado e ergocidade, garantindo ao sistema que sua evolução o leva a estados estacionários de equilibrio descritos pela distribuição de Gibbs relacionada à hamiltoniada de Ising.
O modelo de Ising 2D tratado neste trabalho possui seus spins organizados em uma rede quadrada bidimensional de tamanho com vizinhança de Von Newmann e condições de contorno periódicas. A energia desse sistema é descrita pela equação [1]
onde é a taxa de transição, representa o campo magnético externo e o momento magnético associado com cada spin. O primeiro somatório é sobre todas as vizinhanças de spins e o segundo sobre todos os spins. Neste trabalho, particularmente, escolhemos para favorecer menores energias em spins apontados para cima (), e
A magnetização desse sistema é dada pela soma de todos os valores de spins:
.
Utilizando a abordagem da mecânica estatística, conforme descrito por Gibbs (1902), podemos estimar valores médios de propriedades macroscópicas de um sistema termodinâmico, como energia ou magnetização, a partir de uma amostragem de Boltzmann relativa ao valor da propriedade sobre todos os estados do sistema. Sendo assim, podemos estimar o valor energia do nosso sistema em estado de equilibro termodinâmico como sendo
onde Z é a função partição , é a energia do sistema no estado , é a temperatura de um reservatório em contato com o sistema e é a constante de Boltzmann, escolhida nesse trabalho como tendo valor unitário. O mesmo serve para a magnetização:
, onde é medido sobre o módulo da , que é a magnetização no estado .
Outra medida relevante é a suscetibilidade magnética do sistema, dada por
onde é o número total de spins , e são, respectivamente, a média quadrática da magnetização e média da magnetização durante a simulação. Por fim, temos a medida do calor específico por spin do sistema, dada por
onde e são, respectivamente, a média quadrática da energia do sistema e média da energia durante a simulação.
O Método de Monte Carlo
Algorítmo de Metrópolis
Para o método de Monte Carlo responsável por gerar configurações do sistema, utilizaremos o Algorítmo de Metropolis. O algoritmo funcionará escolhendo repetidamente um novo estado e aceitando ou rejeitando o estado de acordo com uma probabilidade de aceitação de transitar de um estado antigo para o novo estado . O algoritmo que iremos descrever utiliza a dinâmica de inversão única de spins, onde apenas um spin será invertido aleatoriamente para termos um novo estado a ser testado. É válido notar que a dinâmica de inversão única de spins não é o que caracteriza o método de Metropolis, pois ainda poderíamos ter esse método ao utilizarmos uma dinâmica com mais spins sendo invertidos simultaneamente.
Temos que a condição de balanceamento detalhado é dada por [2]:
onde .
Vamos supor que tenhamos os estados e e que temos a relação de energias: . Então, a maior das duas chances de aceitação é , portanto iremos igualar essa probabilidade a 1. Para que seja respeitada, iremos definir o valor de como . Temos, assim, o algoritmo de Metropolis:
Dessa forma, sempre que tivermos um estado cuja energia seja menor do que a do estado atual, iremos aceitar a transição, mas se a energia for maior, teremos uma pequena probabilidade de trocarmos de estado.
Implementação
Para a implementação do método, utilizaremos uma matriz com condições de contorno periódicas, i.e., faremos com que os vizinhos de uma fronteira da matriz sejam os spins na outra fronteira correspondente. Isso irá garantir que todos os spins tenham o mesmo número de vizinhos e a mesma geometria local. Cada spin da matriz poderá assumir apenas os valores de +1 e -1, representando a magnetização desse spin.
Para o estado inicial do sistema, podemos escolher entre duas opções muito utilizadas: ou determinamos e todos os spins, portanto, estarão alinhados na mesma direção, ou assumimos , o que fará com que tenhamos uma configuração aproximadamente aleatória, garantido uma magnetização média do sistema de aproximadamente 0.
Uma boa estratégia para otimizarmos a simulação é calcular a energia total do sistema no estado inicial utilizando a equação e durante a dinâmica da simulação calcularmos apenas , atualizando a nova energia do sistema com . Para obtermos um novo estado, escolhemos aleatoriamente um spin e calculamos a variação de energia ao invertemos ele. Da equação , temos que só um spin irá mudar de estado; logo, apenas seus vizinhos serão afetados. Temos que, para qualquer valor de , . Utilizando isso e fazendo a diferença entre as energias, podemos escrever
onde o somatório se dá nos vizinhos de e, como os vizinhos de não mudam de estado, para qualquer .
De forma similar ao que foi feito para a energia, uma boa estratégia de otimização para a medida da magnetização é calcular a magnetização total do sistema no estado inicial e então somar sempre que o sistema aceitar a mudança de estado. Sendo que para qualquer temos , temos que
Antes de começar o registro das medidas de magnetização e energia do sistema é interessante dar um tempo de equilíbrio para o sistema, ou seja, deixar a simulação ocorrer durante um determinado tempo para eliminar problemas transientes do sistema e o sistema tender a um estado de equilíbrio. Após esse tempo, inicia-se o registro. Os valores do calor específico por spin e da susceptibilidade magnética são feitos após o fim da dinâmica de Monte Carlo.
Durante todo o processo de simulação que fizemos, utilizamos medidas de temperatura em unidades de energia. Dessa forma, temos . Além disso, também utilizamos . Também escolhemos medir o tempo de simulação em passos de Monte Carlo (Monte Carlo steps, ou apenas MCS), que representa o fato de que todos os spins do sistema receberam a chance de inverterem de estado. Em outras palavras, em um sistema com N spins, já ocorreram N seleções aleatórias de spins para tentar a mudança de estado. A partir disso, podemos utilizar o método de amostragem por importância para medir as médias da energia e da magnetização, além das médias da magnetização quadrada e da energia quadrada:
onde é a quantidade de passos de Monte Carlo dadas.
Resultados
Para analisarmos os resultados obtidos pelo método de Metropolis, realizamos diversas medidas em sistemas com dimensões , e . Utilizamos para todas as medidas um tempo de equilíbrio de Monte Carlo Steps e fizemos medidas.
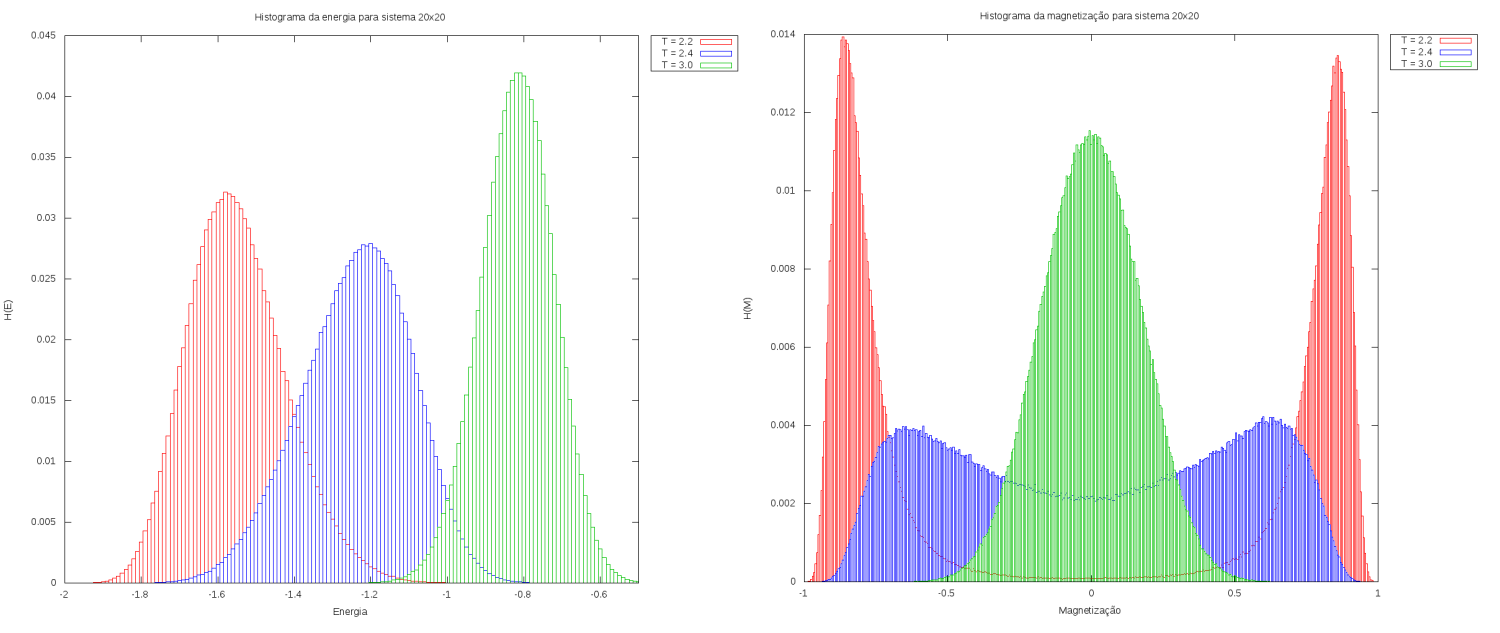
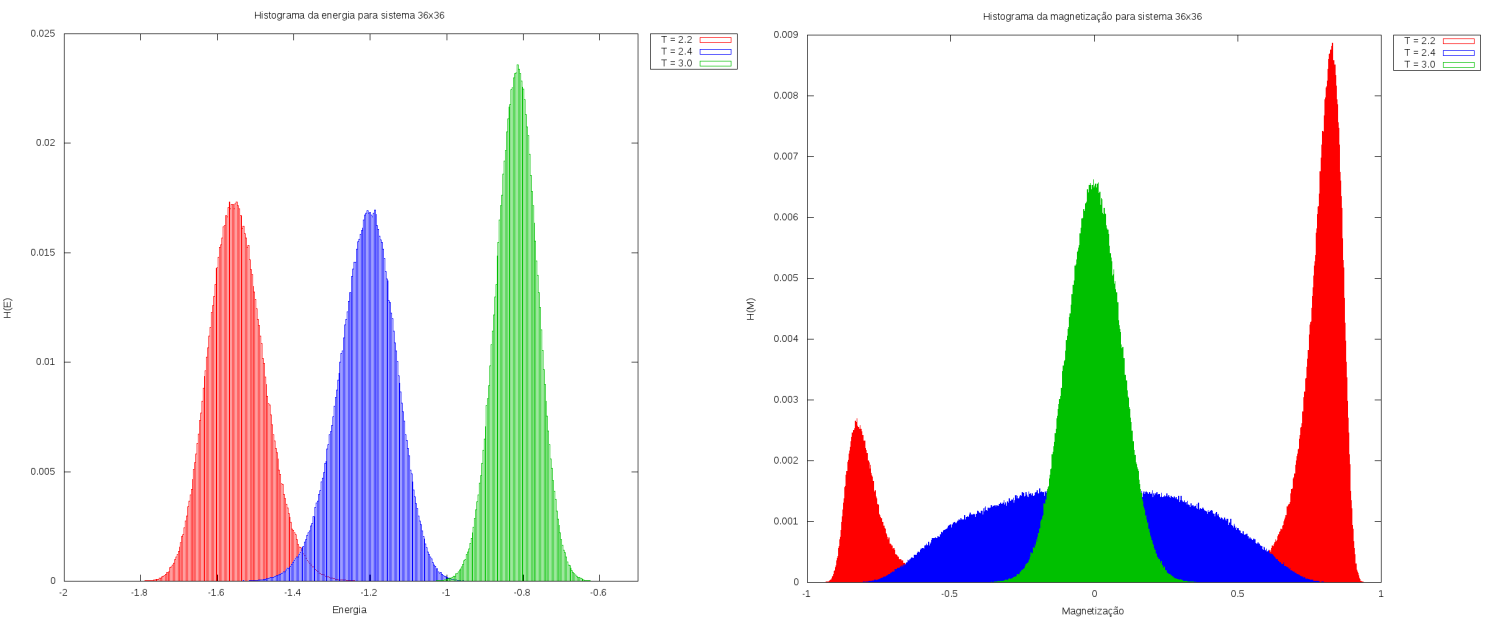
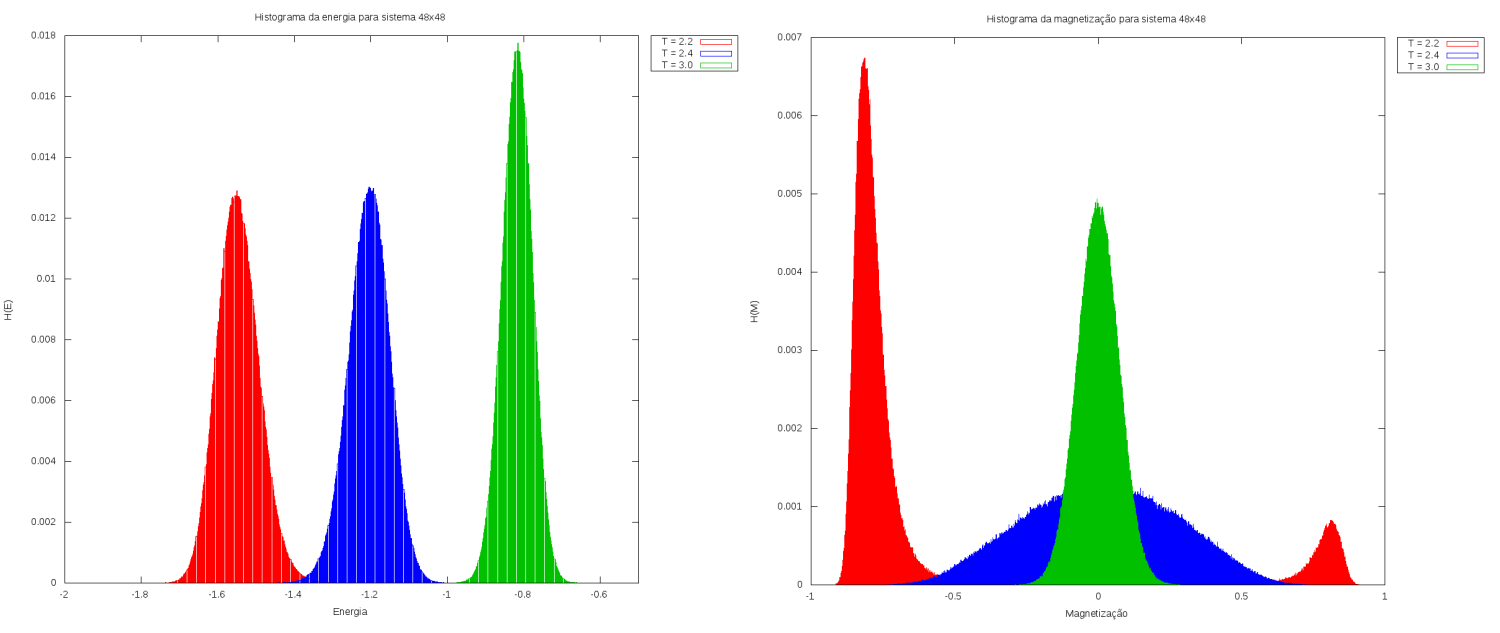
Primeiramente, fizemos medidas para sistemas sem campo magnético, ou seja, . Com isso, montamos histogramas da magnetização por spins e da energia por spins do sistema para cada um dos 3 casos em três diferentes temperaturas:
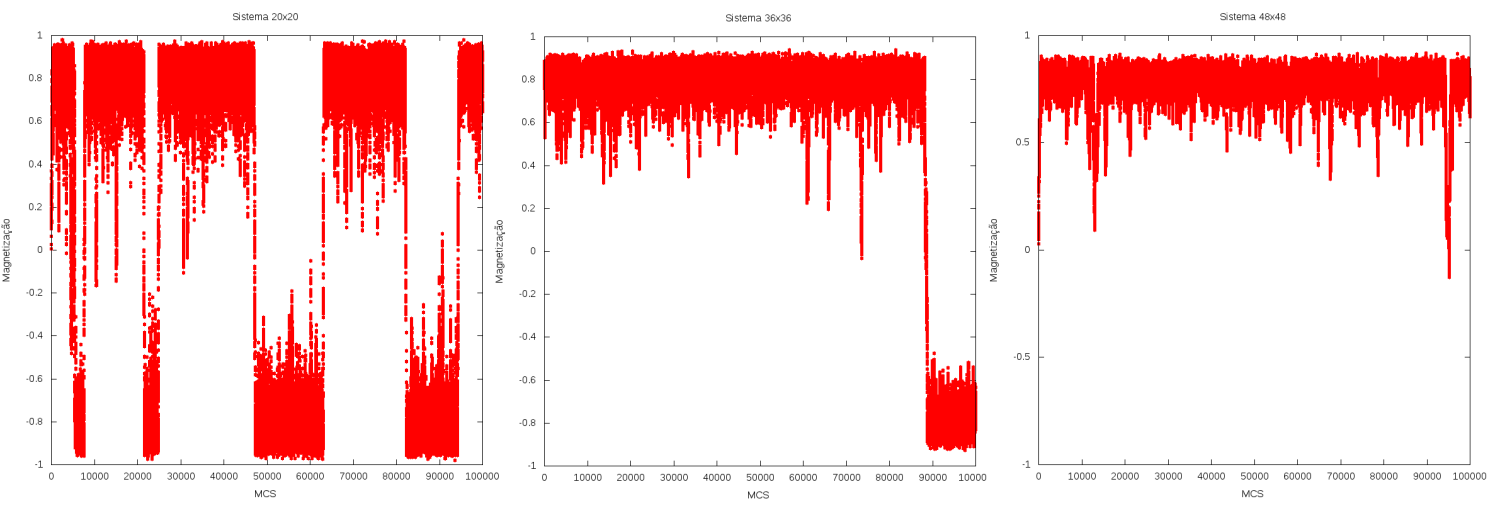
Imediatamente é possível notar que, para todas as temperaturas, quanto maior o número de spins, menor é a variância da energia, com as larguras das gaussianas ficando menores. Para a magnetização, para temperaturas menores que a temperatura crítica e tempos de simulação suficientemente longos, era esperado que tivéssemos duas gaussianas simétricas e de mesma altura, já que os spins estão livres para assumirem valores de +1 e -1. Esse resultado é facilmente observado para no sistema 20x20, mas para os sistemas 36x36 e 48x48 as gaussianas possuem alturas diferentes. Esses resultados são indicativos do efeito de redes maiores, onde temos que quanto maior a rede, menor a probabilidade de haver mudança de magnetização do sistema, exigindo tempos de simulação cada vez maiores. Esse efeito pode ser observado ao compararmos as séries temporais da magnetização dos três sistemas:
Como podemos ver pelas séries temporais, no mesmo período de tempo, o sistema 20x20 troca de estado diversas vezes, enquanto o sistema 36x36 troca apenas uma vez para o estado -1 e o sistema 48x48 não troca nenhuma vez para o estado -1. Além disso, pelos histogramas, é possível notar que quanto maior a temperatura em relação à temperatura crítica, mais a magnetização do sistema tende a zero, ou seja, as duas gaussianas vão se somando em , resultado da transição de fase do ferromagnetismo para o paramagnetismo.
Fazendo um gráfico para a energia em função da temperatura e da magnetização em função da temperatura para cada um dos sistemas, podemos ver que a energia aumenta com o aumento da temperatura, enquanto a magnetização decresce com o aumento da temperatura. Também é possível notar que em ambos os gráficos os resultados para os três tamanhos de sistemas são aproximadamente iguais até a a temperatura aproximar-se da temperatura crítica. Conforme a temperatura se aproxima da transição de fase, os resultados deixam de ser aproximadamente iguais, pois a energia passa a ser maior para redes maiores e voltam a tornarem-se similares após . Para a magnetização, ao se aproximar da transição de fase, a magnetização decresce muito mais rapidamente em redes maiores, com os resultados tendendo a zero com o aumento da temperatura.
Analisando os gráficos da suscetibilidade magnética e do calor específico em função da temperatura, podemos perceber que tanto a suscetibilidade magnética quanto o calor específico aumentam quando a temperatura se aproxima da temperatura crítica, com ambos os gráficos possuindo curvas que se tornam mais estreitas próximo de , com os gráficos sendo mais estreitos em redes maiores. Também podemos ver que ambos os gráficos começam a decair um pouco após a temperatura crítica. Isso significa que as variâncias da energia e da magnetização aumentam consideravelmente com a transição de fase do sistema, implicando no aumento da suscetibilidade magnética e do calor específico ao redor da temperatura crítica. É possível perceber que esse efeito é maior em redes maiores, onde há uma grande diferença entre os valores das redes de diferentes tamanhos. No gráfico com a faixa de temperatura maior, podemos ver que para temperaturas menores que T = 2.1 e maiores que T = 2.8 tanto a suscetibilidade magnética quanto o calor específico possuem valores aproximadamente iguais para todos os tamanhos de rede.
Um resultado de redes grandes
Algo que pode resultar de simulações com redes grandes é o aparecimento de blocos de spins. Em uma rede suficientemente grande, pode ocorrer o aparecimento de aglomerados (clusters) de spins de determinada magnetização e esses aglomerados podem acabar crescendo até que se formem blocos de spins com uma direção que dão um resultado não tão esperado para o sistema. Um exemplo pode ser visto ao simularmos um sistema com temperatura . Nessas condições, o sistema tende a ficar aproximadamente estável com magnetização aproximadamente +1 ou -1. Contudo, eventualmente pode ocorrer de uma simulação acabar com uma magnetização variando próximo de zero, como é possível ver na série temporal:
Ao olharmos um snapshot do estado de ambos os sistemas conseguimos entender o que está acontecendo:
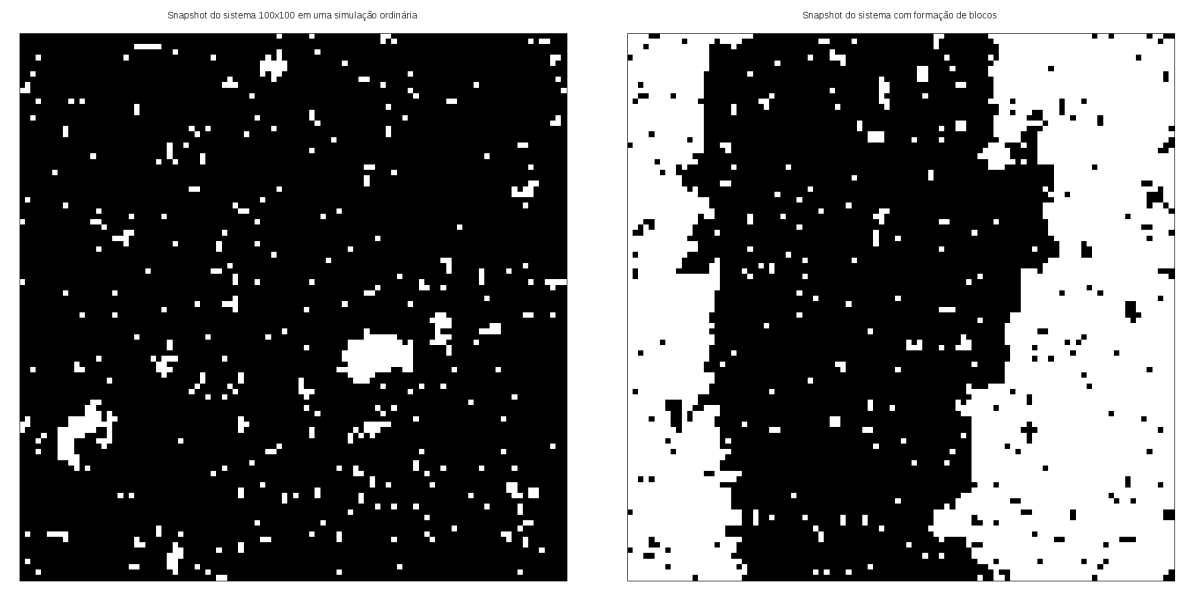
No snapshot da simulação ordinária conseguimos ver que a maior parte dos spins estão com magnetização +1, o que está de acordo com a série temporal. Já no outro snapshot, temos a formação de um bloco de spins com magnetização -1 ocupando uma faixa vertical completa do sistema. Esse estado da rede faz com que spins que sejam invertidos dentro de um dos blocos influenciem muito pouco a magnetização do sistema e os spins das fronteiras entre os blocos que forem invertidos acabam apenas sendo invertidos novamente, fazendo com que a magnetização total do sistema oscile, mas se mantenha sempre próxima do mesmo valor. Para ilustrarmos esse efeito, temos uma animação para cada uma das evoluções: sem a formação de blocos e com formação de blocos.
Simulação com campo magnético
Para fazermos a simulação do modelo de Ising com campo magnético não nulo e termos resultados interessantes de serem observados, precisamos de duas características: primeiro, precisamos que o campo magnético seja pequeno para que possamos fazer observações, pois para campos magnéticos grandes os spins irão se alinhar rapidamente à direção do campo e, portanto, será pouco provável a mudança de estado do sistema. A segunda característica que precisamos é a de que a rede seja pequena, pois quanto maior a rede, menos provável é o sistema mudar de estado em tempos de simulação viáveis, assim como foi visto nos resultados sem campo magnético. Utilizando uma rede 20x20, fizemos histogramas para diferentes temperaturas para dois diferentes campos magnéticos:
Podemos observar que para a temperatura inferior a , temos a formação de uma gaussiana muito maior do que a outra, com a maior gaussiana sendo a que tem a magnetização alinhada com a direção do campo magnético exercendo influencia na rede. Ao utilizarmos temperaturas maiores que a temperatura crítica, vemos a magnetização aumentar ao redor de M = 0, até que em T = 3.0 temos apenas uma gaussiana centrada em M = 0, o que está de acordo com a transição de fase do sistema. Caso não tivéssemos respeitado uma das duas características citadas anteriormente para a simulação de Ising com campo magnético, a maior diferença estaria no sistema com temperatura inferior à temperatura crítica, pois teríamos a formação de apenas uma gaussiana e ela estaria alinhada à direção do campo magnético aplicado ao sistema.
Conclusões e Observações
O modelo de Ising estudado neste trabalho é um modelo de spin extremamente simples. Outros modelos podem ser estudados. Por exemplo, podemos considerar os spins como sendo vetores de comprimento constante mas que tenham movimento de rotação em um plano[1], ou até mesmo considerar vetores em três dimensões[2]. Além disso, o alcance das interações entre os spins do sistema pode ser incrementada para os segundos, terceiros ou até mais distantes vizinhos mais próximos de um spin. Todos esses modelos têm sido estudados extensivamente. Apesar disso, o modelo simples em 2D com spins +1 e -1 estudado ainda representa bem as propriedades do sistema, principalmente o fenômeno de transição de fase.
Programas utilizados em linguagem C
Séries temporais e histogramas sem campo magnético
Magnetização e energia em função da temperatura
Suscetibilidade magnética e calor específico
Animação da evolução do estado do sistema
Série temporal e histograma da magnetização com campo magnético
Referências
Bibliografias
Tânia Tomé, Mário J. de Oliveira, "Stochastic Dynamics and Irreversibility". Universidade de São Paulo, São Paulo, Brasil. 2015.