Modelo de Levins aprimorado para 3 espécies: mudanças entre as edições
(Criou página com '{{Ecologia| Modelo de Levins aprimorado para 2 espécies | Modelo espacialmente explícito }} {{Ecologia| Modelo de Levins aprimorado para 2 espécies | Modelo espaci...') |
Sem resumo de edição |
||
| (6 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[Modelo | {{Ecologia| [[Modelo espacialmente explícito para 2 espécies]] | [[Modelo espacialmente explícito | Modelo espacialmente explícito para 3 espécies]] }} | ||
{{ | Para três espécies o modelo de Levins se torna: | ||
<math display="block">\begin{align} | |||
\frac{dx_{1}}{dt}= & c_{1}x_{1}\left(1-D-x_{1}\right)-e_{1}x_{1}-\mu_{1}x_{1}y \\ | |||
\frac{dx_{2}}{dt}= & x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu_{2}y+c_{x_{1}}x_{1}\right)\right] \\ | |||
\frac{dy}{dt}= & y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right] \\ | |||
\end{align}</math> | |||
====== Guanaco ====== | |||
<math display="block">\frac{dx_{1}}{dt}=x_{1}\left[c_{1}\left(1-D-x_{1}\right)-\left(e_{1}+\mu_{1}y\right)\right]</math>Podemos perceber que é a mesma equação para a presa no modelo de duas [[Modelo de Levins aprimorado para 2 espécies|2 espécies]], proporcional a população atual. | |||
O termo responsável pelo aumento na população é o que representa a colonização. Podemos pensar em termos probabilísticos, que temos 3 eventos independentes: | |||
*Probabilidade <math display="inline">x_{1}</math> de selecionar um fragmento com um guanaco disponível para tentar a colonização; | |||
*Probabilidade <math display="inline">\left(1-D-x_{1}\right)</math> selecionar um fragmento disponível para ser colonizado; | |||
*Probabilidade <math display="inline">c_{1}</math> de que cada tentativa de colonização tenha sucesso. | |||
A queda na população acontece por dois termos que representam dois eventos diferentes: | |||
*Extinção local: depende da taxa <math display="inline">e_{1}</math>. Temos como dois eventos independentes a probabilidade <math>x_1</math> selecionar um fragmento com guanaco e a probabilidade <math>e_1</math> de que cada guanaco sofra a extinção local. | |||
*Predação: depende da população de predadores <math display="inline">y</math> e a taxa de predação <math display="inline">\mu_{1}</math>. Novamente podemos interpretar como três eventos independentes. Probabilidade <math>y</math> de selecionarmos uma puma, probabilidade <math>x_1</math> de selecionarmos um guanaco e probabilidade <math>\mu_1</math> de ocorrer a predação a cada encontro. Assim como o modelo de Lotka-Volterra, a predação é proporcional a população de ambas as espécies. | |||
====== Ovelha ====== | |||
<math display="block">\frac{dx_{2}}{dt}= x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu_{2}y+c_{x_{1}}x_{1}\right)\right]</math> | |||
A ovelha talvez tenha a dinâmica mais complexa do sistema, pois é tanto um competidor inferior ao gunaco, quanto uma presa para o puma, e isso interfere diretamente nos fragmentos disponíveis para a colonização. Pensando em probabilidade e conectando a probabilidade de ocorrer a colonização, é dada pela probabilidade de que cada tentativa de colonização tenha sucesso <math display="inline">c_{2}</math> '''e''' a probabilidade de selecionarmos um fragmento disponível pra as ovelhas é <math display="inline">P\left(F_{D}^{O}\right)</math>. Lembrando que para o caso do guanaco, isso era apenas:<math display="block">P\left(F_{D}^{G}\right)=\left(1-D-x_{1}\right)</math>Pois probabilidade de selecionarmos um fragmento destruído é <math display="inline">D</math>, e de selecionarmos um fragmento ocupado por guanacos é <math display="inline">x_{1}</math>, e são eventos independentes, isto é, nunca temos um fragmento destruído com guanacos. Então a probabilidade de selecionarmos um fragmento que o guanaco não pode colonizar é dado por <math display="inline">D+x_{1}</math>, uma vez que são eventos mutuamente exclusivos. Por complementaridade a probabilidade de selecionarmos um fragmento que o guanaco pode colonizar é dado por <math display="inline">1-\left(D+x_{1}\right)</math>. | |||
Agora precisamos considerar os fragmentos que estão destruídos e os ocupados por ovelhas ou guanacos. Mas a ocupação de guanacos e ovelhas não é exclusiva, isto é, temos fragmentos ocupados por guanacos e ovelhas. Então a probabilidade de selecionarmos um fragmento ocupado por guanaco ou ovelha é dado por <math display="inline">P\left(x_{1}\cup x_{2}\right)=x_{1}+x_{2}-x_{1}x_{2}</math>, uma vez são eventos independentes. Sendo assim a probabilidade de selecionarmos um fragmento indisponível é dado por <math display="inline">D+x_{1}+x_{2}-x_{1}x_{2}</math>. E novamente recorrendo a complementaridade, a probabilidade de selecionarmos um fragmento disponível para a ovelha é dada por então por <math display="inline">1-\left(D+x_{1}+x_{2}-x_{1}x_{2}\right)</math>. | |||
De resto, a população diminui de forma semelhante ao guanaco: | |||
*Termo de extinção local: proporcional a taxa de extinção local <math display="inline">e_{2}</math>; | |||
*Termo de predação: proporcional a população de predadores <math display="inline">y</math> e a taxa de predação <math display="inline">\mu_{2}</math>.; | |||
*Termo de deslocamento: ocorre devido a competição hierárquica e matematicamente é idêntico a predação, apenas substituímos <math>y \rightarrow x_1</math> e <math>\mu_2 \rightarrow c_1</math>. | |||
====== Puma ====== | |||
<math display="block">\frac{dy}{dt}= y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right] </math> | |||
Começando com a parte simples do que já discutimos, a população é reduzida devido a um fator de extinção <math display="inline">e_{y}</math>, e não temos predação, pois o puma é próprio predador. <div class="center">[[Ficheiro:Veinn.png|esquerda|miniaturadaimagem|208x208px|[https://pt.wikipedia.org/wiki/Diagrama_de_Venn Diagrama de Veinn] representando os conjuntos envolvidos no sistema.]] | |||
</div>Agora novamente a parte complexa reside na hora de levarmos em conta a probabilidade de selecionarmos um fragmento disponível. Precisamos considerar todos os fragmentos ocupados ocupados por guanacos ou ovelhas. E quando fazemos isso, precisamos tomar cuidado para não contar duas vezes fragmentos que estejam ocupados por ambas as espécies, então temos <math>P\left(x_{1}\cup x_{2}\right)=P\left(x_{1}\right)+P\left(x_{2}\right)-P\left(x_{1}\cap x_{2}\right)</math>. Além disso, também precisamos descontar os fragmentos que já estão ocupados por pumas, então precisamos descontar os que possuem guanaco e puma <math>P\left(x_{1}\cap y\right)</math> , ovelha e puma <math>P\left(x_{2}\cap y\right)</math>. Porém novamente, não podemos descontar duas vezes os fragmentos que possuem ovelha, guanaco e puma, então é necessário "devolver" <math>P\left(x_{1}\cap x_2\cap y\right)</math>. Temos então: | |||
<math display="block">\frac{dy}{dt}=y\left[c_{y}\left[P\left(x_{1}\cup x_{2}\right)-P\left(x_{1}\cap y\right)-P\left(x_{2}\cap y\right)+P\left(x_{2}\cap y\cap x_{1}\right)\right]-e_{y}\right]</math> <math display="block">\frac{dy}{dt}=y\left[c_{y}\left[P\left(x_{1}\right)+P\left(x_{2}\right)-P\left(x_{1}\cap x_{2}\right)-P\left(x_{1}\cap y\right)-P\left(x_{2}\cap y\right)+P\left(x_{2}\cap y\cap x_{1}\right)\right]-e_{y}\right]</math> | |||
Como são todos eventos independentes:<math display="block">\frac{dy}{dt}=y\left[c_{y}\left[P\left(x_{1}\right)+P\left(x_{2}\right)-P\left(x_{1}\right)P\left(x_{2}\right)-P\left(x_{1}\right)P\left(y\right)-P\left(x_{2}\right)P\left(x_{y}\right)+P\left(x_{1}\right)P\left(x_{2}\right)P\left(x_{y}\right)\right]-e_{y}\right]</math>E substituindo as probabilidades pelas frações:<math display="block">\frac{dy}{dt}=y\left[c_{y}\left[x_{1}+x_{2}-x_{1}x_{2}-x_{1}y-x_{2}y+x_{1}x_{2}y\right]-e_{y}\right]</math> <math display="block">\frac{dy}{dt}=y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right]</math>E como <math display="inline">\left(x_{1}+x_{2}-x_{1}x_{2}\right)=P\left(x_{1}\cup x_{2}\right)</math>, podemos reescrever como:<math display="block">\frac{dy}{dt}=y\left[c_{y}\left[P\left(x_{1}\cup x_{2}\right)-P\left(y\right)P\left(x_{1}\cup x_{2}\right)\right]-e_{y}\right]</math>Ou ainda:<math display="block">\frac{dy}{dt}=y\left[c_{y}\left(1-P\left(y\right)\right)P\left(x_{1}\cup x_{2}\right)-e_{y}\right]</math>Denotando o espaço complementar como <math display="inline">\left(1-P\left(y\right)\right)=P\left(y\right)^{c}</math>:<math display="block">\frac{dy}{dt}=y\left[c_{y}P\left(y\right)^{c}P\left(x_{1}\cup x_{2}\right)-e_{y}\right]</math>Ou seja o termo de colonização é proporcional aos fragmentos ocupados pelas ovelhas e guanacos <math display="inline">P\left(x_{1}\cup x_{2}\right)</math> e os fragmentos livres das pumas <math display="inline">P\left(y\right)^{c}</math> | |||
==== Análise dos pontos de equilíbrio==== | |||
Utilizando o software [https://www.wolfram.com/mathematica/index.html.pt-br?footer=lang Mathematica] pode-se obter os pontos de equilíbrio. Para este conjunto de equações diferenciais, de maneira geral, há 10 pontos de equilíbrio distribuídos da seguinte forma: | |||
[[Ficheiro:pts_es.png|miniaturadaimagem|Posição dos pontos de equilíbrio estáveis à direita e os correspondente autovalores à esquerda.]] | |||
*1 ponto que nenhuma espécie sobrevive <math display="inline">\left(0,0,0\right)</math>; | |||
*1 ponto que apenas o guanaco sobrevive: <math display="inline">\left(x_{j},0,0\right)</math>; | |||
*1 ponto em que sobrevive apenas a ovelha: <math display="inline">\left(0,y_{j},0\right)</math>; | |||
*1 ponto em que sobrevive apenas presas: <math display="inline">\left(x_{j},y_{j},0\right)</math>; | |||
*2 pontos que sobrevivem apenas o guanaco e a puma <math display="inline">\left(x_{j},0,z_{j}\right)</math>; | |||
*2 pontos que sobrevivem apenas a ovelha e a puma <math display="inline">\left(0,y_{j},z_{j}\right)</math>; | |||
*2 ponto que todas espécies sobrevivem <math display="inline">\left(x_{j},y_{j},z_{j}\right)</math>. | |||
Para que seja possível efetuar uma análise, devido a complexidade dos pontos, será utilizado o seguinte conjunto de parâmetros: <math>c_1=0.2</math>,<math>c_2=0.4</math>, <math>c_y=0.06</math>, <math>e_1=0.05</math>, <math>e_2=0.01</math>, <math>\mu_1=0.2</math> e <math>\mu_2=0.8</math>. Pode-se perceber que a destruição do sistema <math>D</math> foi mantida como variável. Utilizando-se então o método de linearização da matriz Jacobiana, tem-se 5 pontos que possuem todos os autovalores negativos em alguma faixa de valores de <math>D</math>. Especificamente: | |||
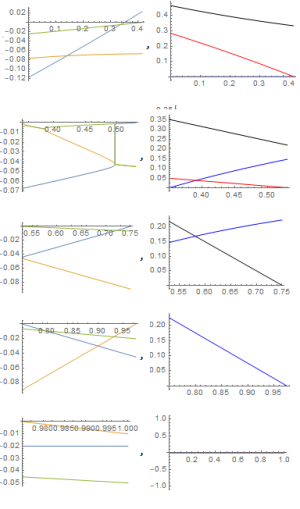
[[Ficheiro:pts_ins.png|miniaturadaimagem|Posição dos pontos de equilíbrio instáveis à direita e os correspondente autovalores à esquerda.]] | |||
*<math display="inline">D<0.35</math>: Guanaco e puma sobrevivem: | |||
**Após <math display="inline">0.35</math> até aproximadamente <math display="inline">0.4</math> este ponto segue sendo um ponto de equilíbrio, mas instável. | |||
*<math display="inline">0.35<D<0.53</math>: Todas as espécies sobrevivem; | |||
*<math display="inline">0.53<D<0.75</math>: Todas as presas sobrevivem; | |||
*<math display="inline">0.75<D<0.975</math>: Somente ovelha sobrevive; | |||
*<math display="inline">0.975<D<1</math>: Nenhuma espécie sobrevive. | |||
2 pontos de equilíbrio que ainda são estados possíveis, mas posuem ao menos um autovalor positivo, isto é, são pontos de equilíbrio instável. Estes pontos não possuem todos os autovalores positivo, o que implica que se o sistema estiver certas direções (dadas pelo autovetores correspondente aos autovalor negativo) vai se aproximar do ponto de equilíbrio. O primeiro ponto é um ponto de estabilidade em uma situação sem guanacos, os 2 autovetores com autovalores negativos estão no plano <math display="inline">x_{2}\times y</math> com <math display="inline">x_{1}=0</math>, ou seja, um sistema sem guanacos se aproximaria deste ponto de equilíbrio. | |||
[[Ficheiro:pts_ss.png|miniaturadaimagem|Posição dos pontos de equilíbrio que não fazem sentido ecologicamente à direita e os correspondentes autovalores à esquerda.]] | |||
E o segundo ponto tem diferentes comportamentos para diferentes faixas de <math display="inline">D</math>. Em um primeiro momento <math display="inline">\left(D<D_{1}\right)</math> os autovetores de autovalor negativo estão em um plano sem predador <math display="inline">x_{1}\times x_{2}</math>. Em um segundo momento <math display="inline">\left(D_{1}<D<D_{2}\right)</math> temos apenas um autovetor apontando no eixo dos guanacos, por fim <math display="inline">D>D_{2}</math> sem ovelhas, isto é, os 2 autovetores estão no plano <math display="inline">x_{1}\times y</math>. Além disso, como comentamos, o primeiro ponto deixa de ser estável a partir de <math display="inline">0.35</math>, este continua sendo um ponto de equilíbrio, apresentando os 2 autovetores com o autovalor negativo no plano <math display="inline">x_{1}\times y</math>, isto é, se não existir ovelhas, é um ponto de estabilidade. Em todo caso, podemos ver que ambos se comportam como estável apenas em situações em que alguma espécie está extinta, ou seja quando já temos um sistema de duas espécies. | |||
Vale destacar que os pontos de equilíbrio fora do ’volume de estados possíveis’ e que possuem algum autovalor negativo, a direção no qual o sistema se aproximaria deste ponto, não passa pelo volume de estados possíveis. Por exemplo, para <math display="inline">D=0.8</math> há um ponto de equilíbrio em <math display="inline">\left(0,0.31,-0.068\right)</math>, o que não é aceitável por possuir uma população de predador negativa. Porém o seu autovalor negativo possui o seguinte autovetor: <math display="inline">\left(-0.29,0.,0.95\right)</math>, ou seja, o sistema nessa direção se aproxima deste ponto de equilíbrio. Porém esta direção não passa pelo volume de estados aceitáveis. | |||
<div class="center">[[Ficheiro:vol.png|centro|miniaturadaimagem|400x200px|À esquerda um ponto de equilíbrio instável fora do volume de configurações aceitáveis e à direita um ponto de equilíbrio também instável, mas aceitável.]] | |||
</div> | |||
Na imagem anterior, à esquerda ponto mencionado anteriormente, mostrando como o autovetor não aponta em uma direção que passe pelo cubo de volumes aceitáveis. Agora, para <math display="inline">D=0.4</math>, o mesmo ponto se desloca para um valor aceitável, <math display="inline">\left(0,0.37,0.10\right)</math>, sem deixar de ser instável. Dois dos seus autovalores são negativos com os correspondentes autovetores <math display="inline">\left(0,1.00,-0.04\right)</math> e <math display="inline">\left(0,-0.91,0.41\right)</math>. Então nestas direções o sistema se aproxima do ponto de equilíbrio, ou seja, apresentam um comportamento estável no plano em que não há guanacos, uma vez que nosso sistema é <math display="inline">\left(x_{1},x_{2},y\right)</math>. Além dos 7 pontos discutidos aqui, há mais 3 pontos que não representam um estado acessível ao sistema, portanto não há interesse em analisá-los. | |||
Plotando as frações ocupada <math display="inline">\times</math> a destruição do sistema, tem-se: | |||
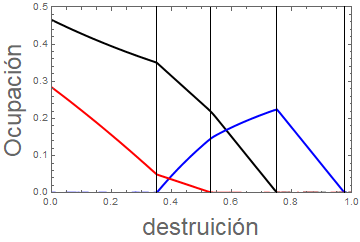
<div class="center">[[Ficheiro:d_var.png|centro|miniaturadaimagem|360x242px|A fração ocupada por cada uma das espécies em função da destruição do sistema.]] | |||
</div>As diferentes condições de coexistência entre as espécies com o sistema em equilíbrio fica evidente. Além disso, plotando em 3 dimensões <math display="inline">\left(e_{y}\times D\times\text{frações ocupadas}\right)</math> tem-se: | |||
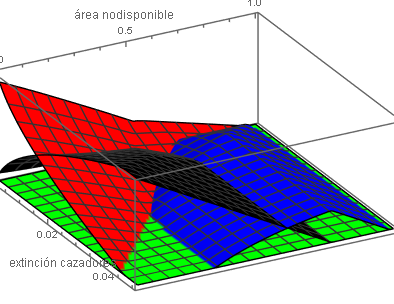
<div class="center">[[Ficheiro:dxey.png|centro|miniaturadaimagem|394x304px|Gráfico em 3 dimensões com a fração ocupada por cada uma das espécies em função da destruição do sistema e da taxa de extinção do predador.]]</div> | |||
Ou ainda como um diagrama de fases <math display="inline">e_{y}\times D\rightarrow\left[0.001,0.05\right]\times\left[0,0.99\right]</math>: | |||
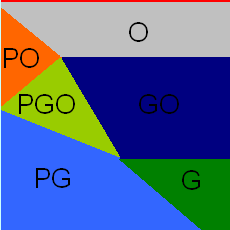
<div class="center">[[Ficheiro:diagrama_fases.png|centro|miniaturadaimagem|230x230px|Diagrama de fase sistema para o conjunto de parâmetros trabalhado.]] | |||
</div> | |||
Pode-se perceber todas combinações possíveis de sobrevivência: as duas presas sozinhas (G,O), presas coexistindo entre si (GO), cada presa coexistindo apenas com o predador (PO,PG), e a coexistência das três espécies (PGO) e ainda para uma faixa próxima <math display="inline">D\approx1</math> a extinção total de todas as espécies. Podemos perceber que a destruição do sistema é o que mais pesa para a sobrevivência ou não das presas, sendo que o Guanaco tem vantagem para valores de destruição mais baixos devido a ser um competidor superior, e as ovelhas para maiores destruições, devido ao suporte humano. | |||
====== Códigos ====== | |||
Os seguintes códigos foram executados no notebook do Mathematica. O primeiro código é responsável por identificar os pontos de equilíbrio do sistema: | |||
Parametros = Rationalize[{c1 -> 4*0.05, c2 -> 4*0.1, cy -> 4*0.015, e1 -> 0.05, e2 -> 0.01, ey -> 0.02, m1 -> 0.2, m2 -> 0.8}]; | |||
dx1 = (c1*x1*(1 - d - x1) - e1*x1 - m1*x1*y)/.Parametros; | |||
dx2 = (x2*(c2*(1 - d - x1 - x2 + x1*x2) - (e2 + m2*y + c1*x1)))/.Parametros; | |||
dy = (y*(cy*((x1 + x2 - x1*x2) - y*(x1 + x2 - x1*x2)) - ey))/.Parametros; | |||
sol = Solve[dx1 == 0 && dx2 == 0 && dy == 0, {x1, x2, y}]; | |||
Os parâmetros podem ser facilmente removidos em caso de interesse. Para um ponto de equilíbrio <math>A</math> , pode-se plotar a dependência da posição do ponto equilíbrio e do autovalor, ambos em relação à <math>D</math>, fazendo: | |||
M = <nowiki>{{D[dx1, x1], D[dx1, x2], D[dx1, y]}, | |||
{D[dx2, x1], D[dx2, x2], D[dx2, y]}, | |||
{D[dy, x1], D[dy, x2], D[dy, y]}}</nowiki> /. Parametros | |||
A = 9; | |||
AV = Eigenvalues[M/.sol<nowiki>[[A]]</nowiki>]; | |||
{Plot[{AV<nowiki>[[1]]</nowiki>, AV<nowiki>[[2]]</nowiki>, AV<nowiki>[[3]]</nowiki>}, {d, 0., 0.415}], | |||
<nowiki> </nowiki>Plot[{sol<nowiki>[[A]]</nowiki><nowiki>[[1]]</nowiki><nowiki>[[2]]</nowiki>, sol<nowiki>[[A]]</nowiki><nowiki>[[2]]</nowiki><nowiki>[[2]]</nowiki>, sol<nowiki>[[A]]</nowiki><nowiki>[[3]]</nowiki><nowiki>[[2]]</nowiki>}, {d, 0., 0.415},PlotStyle -> {Black, Blue, Red}, PlotLegends -> {"Guanaco", "Ovelha", "Puma"}]} | |||
Além disso, pode-se plotar o autovalor e autovetor para um valor para um <math>D</math> em específico: | |||
A = 9; | |||
AV = Eigenvalues[M /. sol<nowiki>[[A]]</nowiki> /. d -> 0.39]; | |||
EV = Eigenvectors[M /. sol<nowiki>[[A]]</nowiki> /. d -> 0.39]; | |||
<nowiki>{{AV[[1]], EV[[1]]}, {AV[[2]], EV[[2]]}, {AV[[3]], EV[[3]]}}</nowiki> | |||
O código abaixo é responsável por resolver numericamente o sistema de equações diferenciais e plotar o resultado: | |||
parametros = Rationalize[{c1 -> 4*0.05, c2 -> 4*0.1, cy -> 4*0.015, e1 -> 0.05, e2 -> 0.01, ey -> 0.02, m1 -> 0.2, m2 -> 0.8}]; | |||
dest = {d -> 0.4}; | |||
tmax = 200; | |||
dsol = NDSolve[{ | |||
c1 x1[t] (1. - d - x1[t]) - e1 x1[t] - m1 x1[t] y[t] == x1'[t], | |||
c2 x2[t] (1. - d - x1[t] - x2[t] + x1[t]*x2[t]) - e2 x2[t] - m2 x2[t] y[t] - c1 x1[t] x2[t] == x2'[t], | |||
cy y[t] (x1[t] + x2[t] - x1[t]*x2[t] - y[t]*(x1[t] + x2[t] - x1[t]*x2[t])) - ey y[t] == y'[t], | |||
x1[0] == 0.2, x2[0] == 0.2, y[0] == 0.2} /. parametros /.dest, {x1, x2, y}, {t, 0, tmax}]; | |||
Plot[{x1[t] /. dsol, x2[t] /. dsol, y[t] /. dsol}, {t, 0, tmax}, PlotRange -> {0, Automatic}, PlotStyle -> {Black, Blue, Red}] | |||
Para plotar o gráfico das frações ocupadas tendo como variável a destruição do sistema: | |||
Manipulate[ | |||
<nowiki> </nowiki>tmax = 10000; | |||
<nowiki> </nowiki>bifu1 = {}; bifu2 = {}; bifu3 = {}; | |||
<nowiki> </nowiki>Do[ | |||
<nowiki> </nowiki> dsol = Quiet@NDSolve[{ | |||
<nowiki> </nowiki> c1 x1[t] (1. - d - x1[t]) - e1 x1[t] - m1 x1[t] y[t] == x1'[t], | |||
<nowiki> </nowiki> c2 x2[t] (1. - d - x1[t] - x2[t] + x1[t]*x2[t]) - e2 x2[t] - m2 x2[t] y[t] - c1 x1[t] x2[t] == x2'[t], | |||
<nowiki> </nowiki> cy y[t] (x1[t] + x2[t] - x1[t]*x2[t] - y[t]*(x1[t] + x2[t] - x1[t]*x2[t])) - ey y[t] == y'[t], | |||
<nowiki> </nowiki> x1[0] == 0.1, x2[0] == 0.1, y[0] == 0.1}, {x1, x2, y}, {t, 0, | |||
<nowiki> </nowiki> tmax} | |||
<nowiki> </nowiki> ]; | |||
<nowiki> </nowiki> AppendTo[bifu1, {d, First[x1[tmax] /. dsol]}]; | |||
<nowiki> </nowiki> AppendTo[bifu2, {d, First[x2[tmax] /. dsol]}]; | |||
<nowiki> </nowiki> AppendTo[bifu3, {d, First[y[tmax] /. dsol]}], {d, 0, 1, 0.01}]; | |||
<nowiki> </nowiki> ListPlot[{bifu1, bifu2, bifu3}, PlotRange -> <nowiki>{{0, 1}, {0, 0.5}}</nowiki>, | |||
<nowiki> </nowiki> Frame -> True, FrameLabel -> {Style["destruición", Large], Style["Ocupación", Large]}, | |||
<nowiki> </nowiki> Joined -> True, PlotStyle -> {Directive[Thick, Black], Directive[Thick, Blue], Directive[Thick, Red]}], | |||
<nowiki> </nowiki> Style["COLONIZACIÓN",Bold], | |||
<nowiki> </nowiki> {{c1, 4*0.05, Style["Competidor superior", Black, Bold]}, 0, 1}, | |||
<nowiki> </nowiki> {{c2, 4*0.1, Style["Competidor inferior", Blue, Bold]}, 0, 1}, | |||
<nowiki> </nowiki> {{cy, 4*0.015, Style["Cazador", Red, Bold]}, 0, 1}, | |||
<nowiki> </nowiki> Style["EXTINCIÓN", Bold], | |||
<nowiki> </nowiki> {{e1, 0.05, Style["Competidor superior", Black, Bold]}, 0, 1}, | |||
<nowiki> </nowiki> {{e2, 0.01, Style["Competidor inferior", Blue, Bold]}, 0, 1}, | |||
<nowiki> </nowiki> {{ey, 0.02, Style["Cazador", Red, Bold]}, 0, 1}, | |||
<nowiki> </nowiki> Style["DEPREDACIÓN", Bold], | |||
<nowiki> </nowiki> {{m1, 0.2, Style["Competidor superior", Black, Bold]}, 0, 1}, | |||
<nowiki> </nowiki> {{m2, 0.8, Style["Competidor inferior", Blue, Bold]}, 0, 1}, | |||
<nowiki> </nowiki> ControlPlacement -> Left, SynchronousUpdating -> False] | |||
E por fim, para gerar o gráfico em 3 dimensões onde além da destruição do sistema <math>D</math> consideramos a taxa de extinção dos predadores também como variável: | |||
Manipulate[ | |||
<nowiki> </nowiki>tmax = 1000; | |||
<nowiki> </nowiki>bifu1 = {}; bifu2 = {}; bifu3 = {}; | |||
<nowiki> </nowiki>Do[ | |||
<nowiki> </nowiki> dsol = NDSolve[{ | |||
<nowiki> </nowiki> c1 x1[t] (1. - d - x1[t]) - e1 x1[t] - m1 x1[t] y[t] == x1'[t], | |||
<nowiki> </nowiki> c2 x2[t] (1. - d - x1[t] - x2[t] + x1[t]*x2[t]) - e2 x2[t] - m2 x2[t] y[t] - c1 x1[t] x2[t] == x2'[t], | |||
<nowiki> </nowiki> cy y[t] (x1[t] + x2[t] - x1[t]*x2[t] - y[t]*(x1[t] + x2[t] - x1[t]*x2[t])) - ey y[t] == y'[t], | |||
<nowiki> </nowiki> x1[0] == 0.01, x2[0] == 0.01, y[0] == 0.01}, {x1, x2, y}, {t, 0, | |||
<nowiki> </nowiki> tmax} | |||
<nowiki> </nowiki> ]; | |||
<nowiki> </nowiki> AppendTo[bifu1, {ey, d, First[x1[tmax] /. dsol]}]; | |||
<nowiki> </nowiki> AppendTo[bifu2, {ey, d, First[x2[tmax] /. dsol]}]; | |||
<nowiki> </nowiki> AppendTo[bifu3, {ey, d, First[y[tmax] /. dsol]}], | |||
<nowiki> </nowiki>{ey, 0., 0.5, 0.02}, {d, 0., 1, 0.05}]; | |||
<nowiki> </nowiki>g1 = ListPlot3D[bifu1, ColorFunction -> "AvocadoColors"]; | |||
<nowiki> </nowiki>g2 = ListPlot3D[bifu2, ColorFunction -> "AtlanticColors"]; | |||
<nowiki> </nowiki>g3 = ListPlot3D[bifu3, ColorFunction -> "SolarColors",PlotRange -> All]; | |||
<nowiki> </nowiki>Show[g1,g2,g3, ViewPoint -> {0, 0, Infinity}, AxesLabel -> {Style["extinción cazadores", Larger], | |||
<nowiki> </nowiki>Style["área nodisponible", Larger], Style["ocupación", Larger]}], | |||
<nowiki> </nowiki>Style["COLONIZACIÓN", Bold], | |||
<nowiki> </nowiki>{{c1, 0.2, Style["Competidor superior", Black, Bold]}, 0, 1}, | |||
<nowiki> </nowiki>{{c2, 0.35, Style["Competidor inferior", Blue, Bold]}, 0, 1}, | |||
<nowiki> </nowiki>{{cy, 0.4, Style["Cazador", Red, Bold]}, 0, 1}, | |||
<nowiki> </nowiki>Style["EXTINCIÓN", Bold], | |||
<nowiki> </nowiki>{{e1, 0.05, Style["Competidor superior", Black, Bold]}, 0, 1}, | |||
<nowiki> </nowiki>{{e2, 0.02, Style["Competidor inferior", Blue, Bold]}, 0, 1}, | |||
<nowiki> </nowiki>Style["DEPREDACIÓN", Bold], | |||
<nowiki> </nowiki>{{m1, 0.3, Style["Competidor superior", Black, Bold]}, 0, 1}, | |||
<nowiki> </nowiki>{{m2, 0.2, Style["Competidor inferior", Blue, Bold]}, 0, 1}, | |||
<nowiki> </nowiki>ControlPlacement -> Left, SynchronousUpdating -> False] | |||
===Principal material utilizado=== | |||
#[https://arxiv.org/pdf/1409.0024.pdf Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances] (Fabiana Laguna e outros, Ecological Modelling) | |||
{{Ecologia| [[Modelo espacialmente explícito para 2 espécies]] | [[Modelo espacialmente explícito | Modelo espacialmente explícito para 3 espécies]] }} | |||
Edição atual tal como às 21h16min de 28 de abril de 2021
Anterior: Modelo espacialmente explícito para 2 espécies | Índice: Ecologia | Próximo: Modelo espacialmente explícito para 3 espécies
Para três espécies o modelo de Levins se torna:
Guanaco
O termo responsável pelo aumento na população é o que representa a colonização. Podemos pensar em termos probabilísticos, que temos 3 eventos independentes:
- Probabilidade de selecionar um fragmento com um guanaco disponível para tentar a colonização;
- Probabilidade selecionar um fragmento disponível para ser colonizado;
- Probabilidade de que cada tentativa de colonização tenha sucesso.
A queda na população acontece por dois termos que representam dois eventos diferentes:
- Extinção local: depende da taxa . Temos como dois eventos independentes a probabilidade selecionar um fragmento com guanaco e a probabilidade de que cada guanaco sofra a extinção local.
- Predação: depende da população de predadores e a taxa de predação . Novamente podemos interpretar como três eventos independentes. Probabilidade de selecionarmos uma puma, probabilidade de selecionarmos um guanaco e probabilidade de ocorrer a predação a cada encontro. Assim como o modelo de Lotka-Volterra, a predação é proporcional a população de ambas as espécies.
Ovelha
A ovelha talvez tenha a dinâmica mais complexa do sistema, pois é tanto um competidor inferior ao gunaco, quanto uma presa para o puma, e isso interfere diretamente nos fragmentos disponíveis para a colonização. Pensando em probabilidade e conectando a probabilidade de ocorrer a colonização, é dada pela probabilidade de que cada tentativa de colonização tenha sucesso e a probabilidade de selecionarmos um fragmento disponível pra as ovelhas é . Lembrando que para o caso do guanaco, isso era apenas:
Agora precisamos considerar os fragmentos que estão destruídos e os ocupados por ovelhas ou guanacos. Mas a ocupação de guanacos e ovelhas não é exclusiva, isto é, temos fragmentos ocupados por guanacos e ovelhas. Então a probabilidade de selecionarmos um fragmento ocupado por guanaco ou ovelha é dado por , uma vez são eventos independentes. Sendo assim a probabilidade de selecionarmos um fragmento indisponível é dado por . E novamente recorrendo a complementaridade, a probabilidade de selecionarmos um fragmento disponível para a ovelha é dada por então por .
De resto, a população diminui de forma semelhante ao guanaco:
- Termo de extinção local: proporcional a taxa de extinção local ;
- Termo de predação: proporcional a população de predadores e a taxa de predação .;
- Termo de deslocamento: ocorre devido a competição hierárquica e matematicamente é idêntico a predação, apenas substituímos e .
Puma
Começando com a parte simples do que já discutimos, a população é reduzida devido a um fator de extinção , e não temos predação, pois o puma é próprio predador.

Agora novamente a parte complexa reside na hora de levarmos em conta a probabilidade de selecionarmos um fragmento disponível. Precisamos considerar todos os fragmentos ocupados ocupados por guanacos ou ovelhas. E quando fazemos isso, precisamos tomar cuidado para não contar duas vezes fragmentos que estejam ocupados por ambas as espécies, então temos . Além disso, também precisamos descontar os fragmentos que já estão ocupados por pumas, então precisamos descontar os que possuem guanaco e puma , ovelha e puma . Porém novamente, não podemos descontar duas vezes os fragmentos que possuem ovelha, guanaco e puma, então é necessário "devolver" . Temos então:
Como são todos eventos independentes:
Análise dos pontos de equilíbrio
Utilizando o software Mathematica pode-se obter os pontos de equilíbrio. Para este conjunto de equações diferenciais, de maneira geral, há 10 pontos de equilíbrio distribuídos da seguinte forma:
- 1 ponto que nenhuma espécie sobrevive ;
- 1 ponto que apenas o guanaco sobrevive: ;
- 1 ponto em que sobrevive apenas a ovelha: ;
- 1 ponto em que sobrevive apenas presas: ;
- 2 pontos que sobrevivem apenas o guanaco e a puma ;
- 2 pontos que sobrevivem apenas a ovelha e a puma ;
- 2 ponto que todas espécies sobrevivem .
Para que seja possível efetuar uma análise, devido a complexidade dos pontos, será utilizado o seguinte conjunto de parâmetros: ,, , , , e . Pode-se perceber que a destruição do sistema foi mantida como variável. Utilizando-se então o método de linearização da matriz Jacobiana, tem-se 5 pontos que possuem todos os autovalores negativos em alguma faixa de valores de . Especificamente:
- : Guanaco e puma sobrevivem:
- Após até aproximadamente este ponto segue sendo um ponto de equilíbrio, mas instável.
- : Todas as espécies sobrevivem;
- : Todas as presas sobrevivem;
- : Somente ovelha sobrevive;
- : Nenhuma espécie sobrevive.
2 pontos de equilíbrio que ainda são estados possíveis, mas posuem ao menos um autovalor positivo, isto é, são pontos de equilíbrio instável. Estes pontos não possuem todos os autovalores positivo, o que implica que se o sistema estiver certas direções (dadas pelo autovetores correspondente aos autovalor negativo) vai se aproximar do ponto de equilíbrio. O primeiro ponto é um ponto de estabilidade em uma situação sem guanacos, os 2 autovetores com autovalores negativos estão no plano com , ou seja, um sistema sem guanacos se aproximaria deste ponto de equilíbrio.
E o segundo ponto tem diferentes comportamentos para diferentes faixas de . Em um primeiro momento os autovetores de autovalor negativo estão em um plano sem predador . Em um segundo momento temos apenas um autovetor apontando no eixo dos guanacos, por fim sem ovelhas, isto é, os 2 autovetores estão no plano . Além disso, como comentamos, o primeiro ponto deixa de ser estável a partir de , este continua sendo um ponto de equilíbrio, apresentando os 2 autovetores com o autovalor negativo no plano , isto é, se não existir ovelhas, é um ponto de estabilidade. Em todo caso, podemos ver que ambos se comportam como estável apenas em situações em que alguma espécie está extinta, ou seja quando já temos um sistema de duas espécies.
Vale destacar que os pontos de equilíbrio fora do ’volume de estados possíveis’ e que possuem algum autovalor negativo, a direção no qual o sistema se aproximaria deste ponto, não passa pelo volume de estados possíveis. Por exemplo, para há um ponto de equilíbrio em , o que não é aceitável por possuir uma população de predador negativa. Porém o seu autovalor negativo possui o seguinte autovetor: , ou seja, o sistema nessa direção se aproxima deste ponto de equilíbrio. Porém esta direção não passa pelo volume de estados aceitáveis.
Na imagem anterior, à esquerda ponto mencionado anteriormente, mostrando como o autovetor não aponta em uma direção que passe pelo cubo de volumes aceitáveis. Agora, para , o mesmo ponto se desloca para um valor aceitável, , sem deixar de ser instável. Dois dos seus autovalores são negativos com os correspondentes autovetores e . Então nestas direções o sistema se aproxima do ponto de equilíbrio, ou seja, apresentam um comportamento estável no plano em que não há guanacos, uma vez que nosso sistema é . Além dos 7 pontos discutidos aqui, há mais 3 pontos que não representam um estado acessível ao sistema, portanto não há interesse em analisá-los.
Plotando as frações ocupada a destruição do sistema, tem-se:
As diferentes condições de coexistência entre as espécies com o sistema em equilíbrio fica evidente. Além disso, plotando em 3 dimensões tem-se:
Ou ainda como um diagrama de fases :
Pode-se perceber todas combinações possíveis de sobrevivência: as duas presas sozinhas (G,O), presas coexistindo entre si (GO), cada presa coexistindo apenas com o predador (PO,PG), e a coexistência das três espécies (PGO) e ainda para uma faixa próxima a extinção total de todas as espécies. Podemos perceber que a destruição do sistema é o que mais pesa para a sobrevivência ou não das presas, sendo que o Guanaco tem vantagem para valores de destruição mais baixos devido a ser um competidor superior, e as ovelhas para maiores destruições, devido ao suporte humano.
Códigos
Os seguintes códigos foram executados no notebook do Mathematica. O primeiro código é responsável por identificar os pontos de equilíbrio do sistema:
Parametros = Rationalize[{c1 -> 4*0.05, c2 -> 4*0.1, cy -> 4*0.015, e1 -> 0.05, e2 -> 0.01, ey -> 0.02, m1 -> 0.2, m2 -> 0.8}];
dx1 = (c1*x1*(1 - d - x1) - e1*x1 - m1*x1*y)/.Parametros;
dx2 = (x2*(c2*(1 - d - x1 - x2 + x1*x2) - (e2 + m2*y + c1*x1)))/.Parametros;
dy = (y*(cy*((x1 + x2 - x1*x2) - y*(x1 + x2 - x1*x2)) - ey))/.Parametros;
sol = Solve[dx1 == 0 && dx2 == 0 && dy == 0, {x1, x2, y}];
Os parâmetros podem ser facilmente removidos em caso de interesse. Para um ponto de equilíbrio , pode-se plotar a dependência da posição do ponto equilíbrio e do autovalor, ambos em relação à , fazendo:
M = {{D[dx1, x1], D[dx1, x2], D[dx1, y]},
{D[dx2, x1], D[dx2, x2], D[dx2, y]},
{D[dy, x1], D[dy, x2], D[dy, y]}} /. Parametros
A = 9;
AV = Eigenvalues[M/.sol[[A]]];
{Plot[{AV[[1]], AV[[2]], AV[[3]]}, {d, 0., 0.415}],
Plot[{sol[[A]][[1]][[2]], sol[[A]][[2]][[2]], sol[[A]][[3]][[2]]}, {d, 0., 0.415},PlotStyle -> {Black, Blue, Red}, PlotLegends -> {"Guanaco", "Ovelha", "Puma"}]}
Além disso, pode-se plotar o autovalor e autovetor para um valor para um em específico:
A = 9;
AV = Eigenvalues[M /. sol[[A]] /. d -> 0.39];
EV = Eigenvectors[M /. sol[[A]] /. d -> 0.39];
{{AV[[1]], EV[[1]]}, {AV[[2]], EV[[2]]}, {AV[[3]], EV[[3]]}}
O código abaixo é responsável por resolver numericamente o sistema de equações diferenciais e plotar o resultado:
parametros = Rationalize[{c1 -> 4*0.05, c2 -> 4*0.1, cy -> 4*0.015, e1 -> 0.05, e2 -> 0.01, ey -> 0.02, m1 -> 0.2, m2 -> 0.8}];
dest = {d -> 0.4};
tmax = 200;
dsol = NDSolve[{
c1 x1[t] (1. - d - x1[t]) - e1 x1[t] - m1 x1[t] y[t] == x1'[t],
c2 x2[t] (1. - d - x1[t] - x2[t] + x1[t]*x2[t]) - e2 x2[t] - m2 x2[t] y[t] - c1 x1[t] x2[t] == x2'[t],
cy y[t] (x1[t] + x2[t] - x1[t]*x2[t] - y[t]*(x1[t] + x2[t] - x1[t]*x2[t])) - ey y[t] == y'[t],
x1[0] == 0.2, x2[0] == 0.2, y[0] == 0.2} /. parametros /.dest, {x1, x2, y}, {t, 0, tmax}];
Plot[{x1[t] /. dsol, x2[t] /. dsol, y[t] /. dsol}, {t, 0, tmax}, PlotRange -> {0, Automatic}, PlotStyle -> {Black, Blue, Red}]
Para plotar o gráfico das frações ocupadas tendo como variável a destruição do sistema:
Manipulate[
tmax = 10000;
bifu1 = {}; bifu2 = {}; bifu3 = {};
Do[
dsol = Quiet@NDSolve[{
c1 x1[t] (1. - d - x1[t]) - e1 x1[t] - m1 x1[t] y[t] == x1'[t],
c2 x2[t] (1. - d - x1[t] - x2[t] + x1[t]*x2[t]) - e2 x2[t] - m2 x2[t] y[t] - c1 x1[t] x2[t] == x2'[t],
cy y[t] (x1[t] + x2[t] - x1[t]*x2[t] - y[t]*(x1[t] + x2[t] - x1[t]*x2[t])) - ey y[t] == y'[t],
x1[0] == 0.1, x2[0] == 0.1, y[0] == 0.1}, {x1, x2, y}, {t, 0,
tmax}
];
AppendTo[bifu1, {d, First[x1[tmax] /. dsol]}];
AppendTo[bifu2, {d, First[x2[tmax] /. dsol]}];
AppendTo[bifu3, {d, First[y[tmax] /. dsol]}], {d, 0, 1, 0.01}];
ListPlot[{bifu1, bifu2, bifu3}, PlotRange -> {{0, 1}, {0, 0.5}},
Frame -> True, FrameLabel -> {Style["destruición", Large], Style["Ocupación", Large]},
Joined -> True, PlotStyle -> {Directive[Thick, Black], Directive[Thick, Blue], Directive[Thick, Red]}],
Style["COLONIZACIÓN",Bold],
{{c1, 4*0.05, Style["Competidor superior", Black, Bold]}, 0, 1},
{{c2, 4*0.1, Style["Competidor inferior", Blue, Bold]}, 0, 1},
{{cy, 4*0.015, Style["Cazador", Red, Bold]}, 0, 1},
Style["EXTINCIÓN", Bold],
{{e1, 0.05, Style["Competidor superior", Black, Bold]}, 0, 1},
{{e2, 0.01, Style["Competidor inferior", Blue, Bold]}, 0, 1},
{{ey, 0.02, Style["Cazador", Red, Bold]}, 0, 1},
Style["DEPREDACIÓN", Bold],
{{m1, 0.2, Style["Competidor superior", Black, Bold]}, 0, 1},
{{m2, 0.8, Style["Competidor inferior", Blue, Bold]}, 0, 1},
ControlPlacement -> Left, SynchronousUpdating -> False]
E por fim, para gerar o gráfico em 3 dimensões onde além da destruição do sistema consideramos a taxa de extinção dos predadores também como variável:
Manipulate[
tmax = 1000;
bifu1 = {}; bifu2 = {}; bifu3 = {};
Do[
dsol = NDSolve[{
c1 x1[t] (1. - d - x1[t]) - e1 x1[t] - m1 x1[t] y[t] == x1'[t],
c2 x2[t] (1. - d - x1[t] - x2[t] + x1[t]*x2[t]) - e2 x2[t] - m2 x2[t] y[t] - c1 x1[t] x2[t] == x2'[t],
cy y[t] (x1[t] + x2[t] - x1[t]*x2[t] - y[t]*(x1[t] + x2[t] - x1[t]*x2[t])) - ey y[t] == y'[t],
x1[0] == 0.01, x2[0] == 0.01, y[0] == 0.01}, {x1, x2, y}, {t, 0,
tmax}
];
AppendTo[bifu1, {ey, d, First[x1[tmax] /. dsol]}];
AppendTo[bifu2, {ey, d, First[x2[tmax] /. dsol]}];
AppendTo[bifu3, {ey, d, First[y[tmax] /. dsol]}],
{ey, 0., 0.5, 0.02}, {d, 0., 1, 0.05}];
g1 = ListPlot3D[bifu1, ColorFunction -> "AvocadoColors"];
g2 = ListPlot3D[bifu2, ColorFunction -> "AtlanticColors"];
g3 = ListPlot3D[bifu3, ColorFunction -> "SolarColors",PlotRange -> All];
Show[g1,g2,g3, ViewPoint -> {0, 0, Infinity}, AxesLabel -> {Style["extinción cazadores", Larger],
Style["área nodisponible", Larger], Style["ocupación", Larger]}],
Style["COLONIZACIÓN", Bold],
{{c1, 0.2, Style["Competidor superior", Black, Bold]}, 0, 1},
{{c2, 0.35, Style["Competidor inferior", Blue, Bold]}, 0, 1},
{{cy, 0.4, Style["Cazador", Red, Bold]}, 0, 1},
Style["EXTINCIÓN", Bold],
{{e1, 0.05, Style["Competidor superior", Black, Bold]}, 0, 1},
{{e2, 0.02, Style["Competidor inferior", Blue, Bold]}, 0, 1},
Style["DEPREDACIÓN", Bold],
{{m1, 0.3, Style["Competidor superior", Black, Bold]}, 0, 1},
{{m2, 0.2, Style["Competidor inferior", Blue, Bold]}, 0, 1},
ControlPlacement -> Left, SynchronousUpdating -> False]
Principal material utilizado
- Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances (Fabiana Laguna e outros, Ecological Modelling)
Anterior: Modelo espacialmente explícito para 2 espécies | Índice: Ecologia | Próximo: Modelo espacialmente explícito para 3 espécies
![{\displaystyle {\begin{aligned}{\frac {dx_{1}}{dt}}=&c_{1}x_{1}\left(1-D-x_{1}\right)-e_{1}x_{1}-\mu _{1}x_{1}y\\{\frac {dx_{2}}{dt}}=&x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu _{2}y+c_{x_{1}}x_{1}\right)\right]\\{\frac {dy}{dt}}=&y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4444c86924b1c8ccbe06e3a0d4daa0810fb7188c)
![{\displaystyle {\frac {dx_{1}}{dt}}=x_{1}\left[c_{1}\left(1-D-x_{1}\right)-\left(e_{1}+\mu _{1}y\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45780c155e0b7dc74b67c355560f93a09a3671fa)










![{\displaystyle {\frac {dx_{2}}{dt}}=x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu _{2}y+c_{x_{1}}x_{1}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8210254bd39cee171327567c3abf27ca544e4fa8)













![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a089f756adf720cbde0c3032e1d6dfdd06dea324)





![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[P\left(x_{1}\cup x_{2}\right)-P\left(x_{1}\cap y\right)-P\left(x_{2}\cap y\right)+P\left(x_{2}\cap y\cap x_{1}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38c975e8999819e0d580c47695965f68bba00c7d)
![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[P\left(x_{1}\right)+P\left(x_{2}\right)-P\left(x_{1}\cap x_{2}\right)-P\left(x_{1}\cap y\right)-P\left(x_{2}\cap y\right)+P\left(x_{2}\cap y\cap x_{1}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47cf55fd2b4caca9fd1da33f7d3fb77f35c59165)
![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[P\left(x_{1}\right)+P\left(x_{2}\right)-P\left(x_{1}\right)P\left(x_{2}\right)-P\left(x_{1}\right)P\left(y\right)-P\left(x_{2}\right)P\left(x_{y}\right)+P\left(x_{1}\right)P\left(x_{2}\right)P\left(x_{y}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d6033cca4b3a2ee2b5f9f820f55c0cc7e26d72c)
![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[x_{1}+x_{2}-x_{1}x_{2}-x_{1}y-x_{2}y+x_{1}x_{2}y\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b75ceec5c4bc7ad9cde132a44759580d3b13a2)

![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[P\left(x_{1}\cup x_{2}\right)-P\left(y\right)P\left(x_{1}\cup x_{2}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5654970881fed4773c29673c7e349eb86928f8ad)
![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left(1-P\left(y\right)\right)P\left(x_{1}\cup x_{2}\right)-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17993cbe44dcac8c5e0009ac8b8fd485783da74)

![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}P\left(y\right)^{c}P\left(x_{1}\cup x_{2}\right)-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6210c695ef59c0ebb4895556a7efe5c5fa1fc2ff)












































![{\textstyle e_{y}\times D\rightarrow \left[0.001,0.05\right]\times \left[0,0.99\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8981961e3ad24c5f69f44d86b170d243ec940947)