Medidas estáticas

Em dinâmica molecular, medidas estáticas são medidas realizadas em um passo específico de tempo da simulação.

Pair Distribution Function

Representação do cálculo numérico de $g(r)$;

A Pair Distribution Function , ou "$g(r)$", é uma função que estima o quão provável é encontrar duas partículas a uma distância $r$ dentro de um sistema de várias partículas.

Em um sistema de $N$ partículas, o $g(r)$ é definido como a média do número de partículas a uma distância $r$:

$g(r)={\frac {V}{N^{2}}}\langle \sum _{i=1}^{N}\sum _{j\neq i}^{N}\delta (r-|r_{i}-r_{j}|)\rangle$

Numéricamente pode ser interpretado como a média do número de pares de partículas a uma distância entre $r$ e $r+\Delta r$ pesado pelo volume/área desta região.

$g(r,\Delta r)={\frac {V_{t}}{N^{2}}}\sum _{i=1}^{N}\sum _{j\neq i}^{N}\left[{\frac {rect\left({\frac {r-|r_{i}-r_{j}|}{\Delta r}}\right)}{V\left(r+{\frac {\Delta r}{2}}\right)-V\left(r-{\frac {\Delta r}{2}}\right)}}\right]$

Onde $V_{t}$ é o/a volume/área total e $rect$ é a função retangular.

Em resumo, o $g(r,\Delta r)$ é a média dos histogramas do número de partículas em um bin de largura $\Delta r$ a uma $r$ feitos para cada partícula no sistema pesado pelo volume/área deste bin.

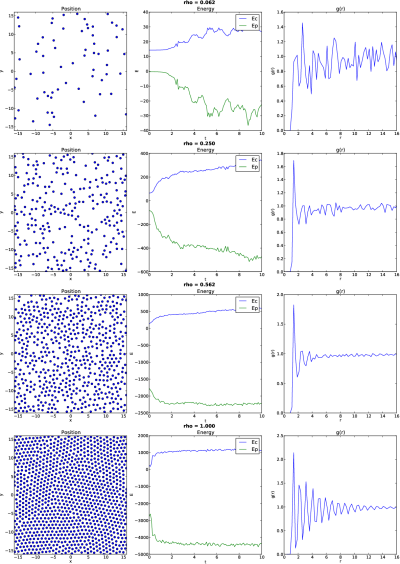
Resultados

Referências

• Frenkel, Daan and Smit, Berend (2001). Understanding Molecular Simulation. Academic Press.

Psi 6 ($\psi _{6}$)

No estudo do agrupamento de pontos equidistantes em um espaço 2D, é possível provar matematicamente que o formato formado pelos pontos que maximiza a utilização do espaço é o padrão hexagonal. Para dinâmicas moleculares com potenciais de Lennard-Jones com densidade suficientemente alta (rho ~0.8) é possível observar que o padrão formado após o relaxamento (tempo suficiente para a rede se estabilizar) é de fato o padrão hexagonal.

O psi 6 é uma análise de o quão hexagonal um padrão de posições está em um certo tempo da simulação. É possível associar a cada partícula um valor que varia entre -1 e 1 da hexagonalidade do padrão de posições formado por ele e seus primeiros vizinhos (conjunto de partículas mais próximas). Com essa medida é possível quantificar diferentes regiões da "caixa" em que as partículas estão localizadas e então localizar possíveis "defeitos" no padrão hexagonal.

Para um padrão hexagonal perfeito, cada partícula apresenta 6 primeiros vizinhos, cada qual posicionado simetricamente em torno dessa. Analisando a simetria, cada vizinho consecutivo deve apresentar um ângulo de ${\frac {\pi }{3}}$. Buscando uma relação em que esta situação seja a situação de $\psi _{6}=1$, é possível definir que o $\psi _{6}$ vale:

$\psi _{6}={\frac {1}{6}}\sum _{i}^{n}cos(6\theta _{i})$

Onde i é o índice do i-ésimo vizinho e n é o número de primeiros vizinhos. Esta relação deixa específico que o caso de 6 primeiros vizinhos e $\theta ={\frac {\pi }{3}}$ resulte em um valor de $\psi _{6}=1$.

Implementação Computacional

Definição de vizinhança:O primeiro círculo pontilhado delimita os primeiros vizinhos, o segundo círculo pontilhado delimita os segundos vizinhos;

Pode-se separar a implementação computacional em dois procedimentos necesssários: Encontrar os primeiros vizinhos para cada partícula e então calcular, de fato, o valor de $\psi _{6}$.

Encontrando vizinhos

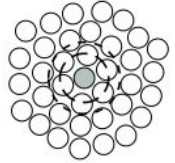
Por definição, os primeiros vizinhos de uma partícula são aquelas partículas que estão presentes em um anel mais próximo dela, como mostra a figura ao lado.

O problema de encontrar primeiros vizinhos é um problema bastante discutido em teoria da computação e diversos métodos foram desenvolvidos para efetuar esta tarefa. Desta forma a maioria dos métodos otimizados são de difícil implementação e então não serão tratados nesse verbete.

O método aqui citado é pouco otimizado, pois utiliza-se um for em $N^{2}$, porém de implementação razoavelmente simples. O método consiste em encontrar as partículas mais próximas da partícula-teste (partícula em que busca-se calcular o valor de $\psi _{6}$ baseando-se em outro valor já calculado, a medida do g(r), desta forma o valor de $\psi _{6}$ resultará em um valor razoável ( >0.8 ) se os vizinhos dentro do raio medido no g(r) são de fato 6 e estão localizados em um padrão quase-hexagonal em torno da partícula-teste.

Para encontrar os primeiros vizinhos baseando-se no g(r), precisa-se observar qual a medida do primeiro pico no gráfico do g(r) e então definir este como uma distância de corte para a partícular ser ou não vizinha (isto é, um circulo com o raio da distância de corte ao redor da partícula-teste de forma que outras partículas dentro deste círculo são suas vizinhas). Neste caso, definem-se três vetores: "neighborsX" (que guarda a posição X do vizinho), "neighborsY"(que guarda a posição Y do vizinho) e "dNeighbors"(que guarda a distância do vizinho)[É recomendado definir estes vetores com tamanho pelo menos de 10, pois é possível que sejam encontrados mais de 6 vizinhos, para isso existe a variável de controle "k" que guarda quantos vizinhos cada partícula tem] e então faz-se o for em $N^{2}$ buscando-se as distância menores que o raio de corte:

	for(i=0;i<NP;i++){
                k=0;
                xOrg=xx[i];
		yOrg=yy[i];
		for(j=0;j<NP;j++){
			x2=xx[j];
			y2=yy[j];
			if(i!=j){
                                deltaX=fabs(x2-x1);
                        	deltaY=fabs(y2-y1);
                                //Condições de contorno
                                deltaX=deltaX-rint(deltaX/Lx)*Lx;
                                deltaY=deltaY-rint(deltaY/Ly)*Ly;
                                // --- //
                                d=sqrt((deltaX*deltaX)+(deltaY*deltaY));
				if(d<radiusLimit)
				{	
					neighborsX[k]=x2;
					neighborsY[k]=y2;
					dNeighbors[k]=d;
					k+=1;
				}
			}		
                 }

Portanto após esse algoritmo, temos guardadas as posições das partículas mais próximas. É importante ressaltar que o "for" em partícula-teste ainda não foi fechado, e ainda dentro deste mesmo loop serão calculados os valores de $\psi _{6}$.

Calculando o Psi 6

Tendo os valores de X e Y dos vizinhos da partícula-teste, podemos proceder para o cálculo do $\psi _{6}$. Para este cálculo, precisamos dos ângulos que cada vizinho tem em relação a partícula-teste, isto é, setamos um referencial X-Y com a origem na partícula-teste e calculamos o ângulo que cada vizinho tem com o eixo X, este ângulo será chamado de $\phi$ e será dado pela seguinte relação:

$\phi _{i}=arctg\left({\frac {\Delta Y}{\Delta X}}\right)$

Na implementação em código fica:

	for(j=0;j<k;j++){
		delX=neighborsX[j]-xx[i];
		delY=neighborsY[j]-yy[i];

                //Condições de contorno periódicas
		delX=delX-rint(delX/Lx)*Lx; 
        	delY=delY-rint(delY/Ly)*Ly;
                // --- //

		angle[j]=atan2(delY,delX);
		if (angle[j]<0)
			angle[j]=2*PI+angle[j];
                psix[i]=0;
 

Agora somente precisa-se realizar um algoritmo que ordene o vetor "angle" do menor para o maior ângulo, utilizando algoritmos de ordenamento (bubblesort, quicksort, etc) desta forma é possível calcular os $\theta _{i}$.

Feito o ordenamento do vetor, basta calcular a média do valor do $\psi _{6}$ de cada vizinho. Para isto, precisamos calcular os valores de $\theta _{i}$ em função dos $\phi$, basta realizar a subtração do próximo vizinho no vetor pelo valor do ângulo do vizinho atual, dessa forma: $\theta _{i}=\psi _{i+1}-\psi _{i}$ com exceção do último vizinho, que será o ângulo dele menos o do primeiro, desta forma a implementação fica:

		firstAngle=angle[0];	
		for(j=0;j<k-1;j++){ 
			angle[j]=cos(6.*(angle[j+1]-angle[j]));
		}		
		angle[k-1]=cos(6.*(firstAngle+2*3.1415-angle[k-1]));
		for(j=0;j<k;j++){ 
			psix[i]+=angle[j]/6.;
		}	
	}
}

E então está calculado o valor de $\psi _{6}$, para facilitar a implementação é recomendado que este algoritmo seja uma função dentro de seu código e desta forma retorne o vetor "psix".

Exemplos

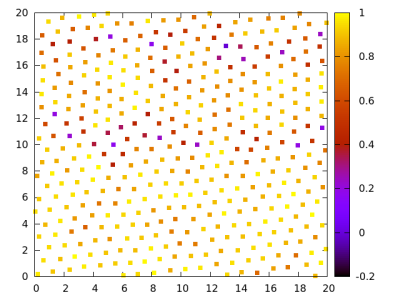
Para o caso de um potencial de Lennard-Jones, é possível observar resultados de mapas de $\psi _{6}$, isto é, um mapa que mostra para cada partícula o seu valor da medida, da seguinte forma para cada valor de rho:

Resultados do valor de $\psi _{6}$ (em cores) para o caso de um potencial de Lennard Jones para $\rho =1.000$

Resultados do valor de $\psi _{6}$ (em cores) para o caso de um potencial de Lennard Jones para $\rho =0.360$.

Resultados do valor de $\psi _{6}$ (em cores) para o caso de um potencial de Lennard Jones para $\rho =0.640$

Aplicações em outras áreas

Mapa neural de células de grade em que o valor de $\psi _{6}$ equivale 0,99.

No estudo de como animais processam a sua posição em seu cerébro, são observadas as chamadas "Células de grade", neurônios que disparam em certos locais específicos do espaço e tendem a formar padrões de grade (hexagonal). Em posse das posições de disparo desses neurônios é possível utilizar a medida do $\psi _{6}$ para determinar a "hexagonalidade" dos disparos, podendo-se realizar estudos da influência desse formato na interpretação geoespacial do animal.