Grupo - Solução Exata para Movimento Anisotrópico de Ornstein-Uhlenbeck
Aluno: Juliano Almeida Machado - Física
Introdução
Movimento coletivo ordenado de diversos organismos é um fenômeno que pode ser observado em diversas situações, como em movimento de cardumes, migração de pássaros, migração celular, etc..
Aquilo que é mais curioso destes tipos de movimento é que o mesmo surge através de movimentos aleatórios dos indivíduos que o compõem, ou seja, o movimento individual e aleatório de um grupo de células quando postos a interagir entre si leva a um movimento ordenado em curtas escalas de tempo.
Um dos modelos anteriores a este, o modelo de Vicsek [1], visa descrever o movimento coletivo ordenado de partículas “inteligentes”, isto é, partículas que podem observar as outras partículas na vizinhança e mover-se de acordo com a média do movimento do grupo. Um bom exemplo disso é o movimento de pássaros ou peixes, da onde movimentos ordenados podem emergir de movimentos aleatórios dos indivíduos autopropulsionados. Curiosamente, mesmo que estes sistemas estejam longe de um estado de equilíbrio, os mesmos apresentam características típicas de sistemas no equilíbrio, como transições de fase bem definidas.
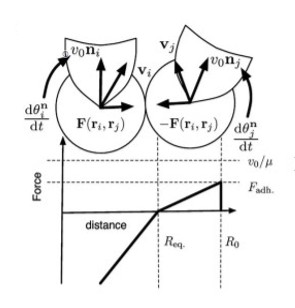
Contudo, partículas “não inteligentes” já haviam demonstrado o mesmo tipo de movimento coletivo experimentalmente, com as mesmas mudanças de fase bem definidas. É para explicar isso, que o modelo de Szabó (Grupo - Modelo de Szabó) foi criado. Nele, o mesmo fenômeno é descrito utilizando somente as forças de interação intercelulares já que isso é algo que independe da capacidade da célula de poder observar a média do movimento da vizinhança, como em Vicsek.
Essas forças são repulsivas para distâncias () menores que , sendo o seu máximo para esse caso, atrativa para , sendo o máximo para esse caso, e zero para maior que um certo .
Essas forças levam às seguintes equações de movimento:
Onde é o número de partículas e é o somatório da todas as interações sobre uma partícula i.
Onde é o tempo de relaxamento, é o vetor na direção de polarização, tal que , é o vetor normal, e é um ruído branco.
Neste modelo, o movimento bidimensional das células é descrito por uma dinâmica superamortecida. Na mesma, cada célula tenta manter uma velocidade de magnitude na direção do vetor , sendo que a direção desse vetor é descrita pelo ângulo que tenta relaxar na direção da velocidade enquanto sofre ruído gaussiano.
Embora descreva bem este movimento, o modelo de Szabó fornece somente soluções numéricas para o problema. Para obtermos uma solução analítica, o problema precisa ser descrito de outra forma. É com esse objetivo que o modelo de Rita et al. foi feito.
Modelo
Neste modelo, em vez de ter a relaxação da velocidade na direção da polarização, a mesma é projetada sobre a polarização, enquanto ela muda com ruído. Essa direção de polarização interna pode representar, p.e., a polarização dos filamentos de actina na direção preferencial em migração celular.
Com isso pode-se observar duas transições, ou seja, uma transição de um estado desordenado para um estado ordenado e para um estado desordenado de novo. Essas duas transições representam a aleatoriedade do movimento inicial das células, depois a escolha de uma direção preferencial e por último a variação desta direção preferencial.
Contudo, neste modelo deve-se assumir que, para a partícula, seu movimento é anisotrópico, ou seja, apresenta assimetria nas dinâmicas de movimento em direções diferentes, uma na direção paralela à direção de polarização e outra perpendicular.
Movimento Paralelo
Na direção paralela à polarização, temos o sistema agindo numa dinâmica semelhante a de Langevin ()[2], mais especificamente, um processo de Orstein-Uhlenbeck amortecido. Nesta direção a velocidade (paralela) é bem definida. Tanto para o movimento paralelo, quanto para o movimento perpendicular, é o vetor que indica a direção de polarização e é o vetor perpendicular a .
Onde é a velocidade paralela, é o coeficiente de atrito e é o ruído gaussiano paralelo.
A velocidade diminui por causa do atrito com o substrato, já que pode-se observar que tende a se for pequeno, e diminui ou aumenta por causa do termo estocástico . A primeira equação assume que durante o intervalo , a direção de polarização é constante. Somente em , a velocidade na direção é projetada sobre a nova direção de polarização .
Movimento Perpendicular
Na direção perpendicular à polarização, o sistema segue um processo de Wiener (movimento aleatório) por causa das flutuações na direção de polarização.
Onde é o ruído gaussiano na direção perpendicular. Pode-se observar que . Este movimento, por ser puramente um processo de Wiener, é melhor descrito pelo deslocamento do que pela velocidade.
Ângulo e Ruídos
A direção de polarização é definida pelo ângulo teta que também apresenta ruído branco. Esse ruído é relacionado à através de . É essa mudança na direção de polarização que causa o deslocamento aleatório perpendicular.
Embora o ruído no ângulo e o ruído na direção perpendicular estejam relacionados, os mesmos são independentes do ruído na direção paralela. Abaixo pode-se ver a correlação dos mesmos. Os três são ruídos gaussianos, então a média deles é zero.
Onde tem unidades de 1/tempo, tem unidades de comprimento, e tanto quanto tem unidades de [comprimento]^2 / tempo.
Em resumo, este modelo considera uma partícula com dois graus de liberdades espaciais e um grau de liberdade interna, que considera a polarização interna. Esse grau de liberdade interna quebra a simetria espacial de tal forma que a dinâmica na direção da polarização é semelhante a Langevin e na direção perpendicular a dinâmica segue um processo de Wiener. Existem duas fontes independentes de ruído: Uma age na dinâmica na direção de polarização e a outra age na polarização em si. Além da força de dissipação, a mudança na polarização age como mais um termo na perda de energia cinética.
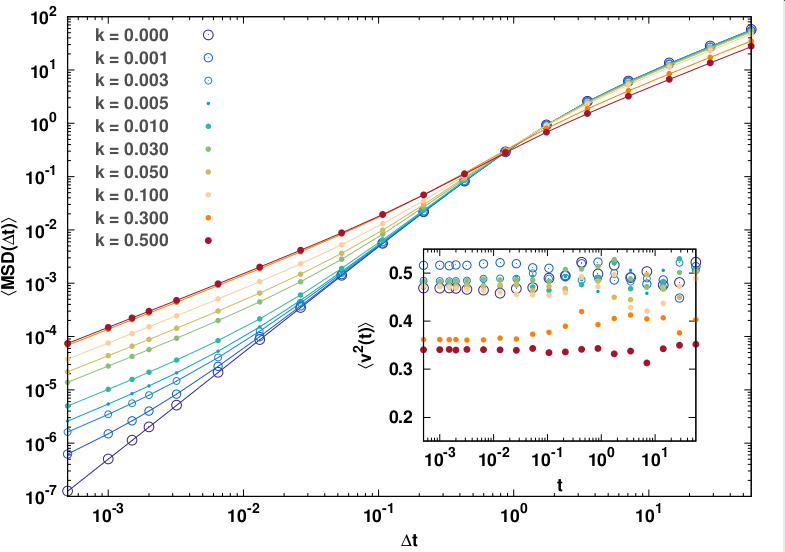
Mean Square Displacement(MSD)
O MSD é uma quantificação do movimento líquido das partículas. O mesmo foi utilizado para medir a aglomeração e a transição de fase das mesmas. Para isso foi feita uma média do MSD de 100 trajetórias sendo que o Método das Janelas foi feito para cada uma das mesmas. Através do resultados analíticos para as equações de movimento pode-se obter um resultado analítico para o MSD também:
Onde é o tempo de persistência do movimento em um estado cinético, é uma fração deste tempo, relacionado a quanto tempo o movimento persiste no primeiro estado cinético e , sendo que e .
Para testar este modelo resolveu-se numericamente as equações diferenciais de movimento com um algoritmo simples de Euler-Maruyama e comparadas com os resultados analíticos do MSD para diferentes valores do parâmetro .
O resultado obtido consta abaixo. Nele os pontos são os valores obtidos pela simulação e as linhas são as previsões da solução analítica para o MSD. No mesmo pode-se claramente ver as duas transições de estado cinético, especialmente para valores pequenos de .
O Programa
O programa criado para gerar simulações do modelo descrito e calcular o MSD do mesmo foi feito em C. O mesmo começa com uma inialização de todas as variáveis necessárias e a definição das mesmas de acordo com aquilo que foi descrito acima sendo os parâmetros iniciais: e e os parâmetros termodinâmicos e que descrevem o comportamento macroscópico da célula.
//Escrito por Mendeli Vainstein;
#define N 100
#define GAMMA 1.0 //3.0
#define M 1.0 //5.0
#define G 1.0 //7.0
#define K 0.00 // 0.01 //0.001
#define T_MAX (1e2) // 1e2 //5e1 //1e2 //5e2
#define DT (1e-4) // 1e-5//1e-5 //1e-6
#define TRANSIENT (2e1)
#define NUM_CORR_MEASURES 200
#define NUM_VCORR_MEASURES 200
#define T_MAX_VCORR 20
unsigned long int rseed;
double *rx,*dr_par,*vpar,*dx,*dy;
double *ry,*dr_perp,*vperp;
double *v2, *corr_v, *r2, *v2_ave,*v_ave, *corr_v_ave;
double K;
int N, MAX_STEPS, TRANSIENT_STEPS, STEP_SIZE_VCORR;
long corr_time[NUM_CORR_MEASURES];//, vcorr_time[NUM_VCORR_MEASURES];
double TAUB, GAMMA_M, TAU2,GAMMA_M2,V02;
double DT_DIV_2,M2, TAU, Q, SQRT_Q;
double EXP_VPAR, SQRT_DT;
double XI_PAR,XI_PAR_SQRT_DT,XI_PAR_SQRT_DT_DIV_M;
double XI_THETA,XI_THETA_SQRT_DT; // Used if langevin theta dynamics
double *theta, *d_theta;
double two_PI = 2*M_PI;
const gsl_rng_type * T;
gsl_rng * rand_vec;
char filename[200];
FILE *fcorr, *ftraj, *fr2;
/************************************************************************************************
* *
************************************************************************************************/
void allocate_pointers(int n);
void free_pointers(int n);
void measure(double *rx, double *ry,double *rx0, double *ry0, double *v2, unsigned long int t);
void set_initial_conditions(int N);
void set_correlation_vecs();
void calculate_correlations(double *rx, double *ry, double *v);
void print_correlations(void);
void reset_initial_condition(int t_counter);
void set_gsl_rng(void);
double wrap_angle(double theta);
void create_time_table(long *t1, int total_time, int measures);
/************************************************************************************************
* *
************************************************************************************************/
Inicialização:
void set_constants(void)
{
MAX_STEPS = (int)(T_MAX/DT) + 1;
TRANSIENT_STEPS = TRANSIENT/DT;
DT_DIV_2 = 0.5*DT;
SQRT_DT = sqrt(DT);
M2 = M*M;
TAU = GAMMA/M + K;
TAU2 = TAU*TAU;
TAUB = GAMMA/M + 2*K;
GAMMA_M = GAMMA/M;
GAMMA_M2 = GAMMA_M*GAMMA_M;
XI_THETA = sqrt(2.0*K);
XI_THETA_SQRT_DT = XI_THETA * SQRT_DT; // Used if langevin theta dynamics
XI_PAR = sqrt(G); //sqrt(2.0*(GAMMA+K*M)*kT);
XI_PAR_SQRT_DT = XI_PAR * SQRT_DT;
XI_PAR_SQRT_DT_DIV_M = XI_PAR * SQRT_DT/M;
EXP_VPAR = exp(-DT_DIV_2*GAMMA/M); //For langevin algorithm
V02 = G/(2*M2*TAU); //G/(2*M2*(GAMMA/M + K))
Q = V02/TAU2; //(kT/M)/TAU2;//v2/(TAU*TAU);
SQRT_Q = sqrt(Q);
create_time_table(corr_time, MAX_STEPS, NUM_CORR_MEASURES);
//create_time_table(vcorr_time, T_MAX_VCORR/DT, NUM_VCORR_MEASURES);
STEP_SIZE_VCORR = T_MAX_VCORR/(NUM_VCORR_MEASURES*DT);
return;
}
Em seguida foram definidas as funções que iriam calcular a dinâmica descrita acima, sendo que cada parte foi feita numa função separada (p.e. a dinâmica paralela e a perpendicular). Com isso polarizações e velocidades iniciais foram atribuidas, tal que as mesmas começassem em equilibrio.
double msd_analitico (double t)
{
return (G/(M2*TAUB*TAU)) * (t - (1.0-exp(-TAUB*t))/TAUB) + 2*Q*K*t;
}
/************************************************************************************************
* *
************************************************************************************************/
void set_gsl_rng(void)
{
#ifdef DEBUG
rseed=0;
#else
rseed=time(NULL);
#endif
gsl_rng_env_setup();
T = gsl_rng_default;
rand_vec = gsl_rng_alloc (T);
gsl_rng_set (rand_vec, rseed);
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void open_output_files(void)
{
sprintf(filename,"corr_K_%.2e_N_%d.txt",K,N);
fcorr = fopen(filename,"w");
fprintf(fcorr,"#Delta t\t vcorr\n");
sprintf(filename,"traj_K_%.2e.txt",K);
ftraj = fopen(filename,"w");
fprintf(ftraj,"#t\t x\t y\n");
sprintf(filename,"r2_K_%.2e_N_%d.txt",K,N);
fr2 = fopen(filename,"w");
fprintf(fr2,"#Delta t\t r2\t r2_exact\t vcorr\n");
return;
}
Dinâmicas (Euler-Maruyama[3]):
/************************************************************************************************
* *
************************************************************************************************/
void dynamics_r_parallel(int tstep)
{
/**********************************************************************
* dv_par/dt = -gamma/m v_par + (1/m) xi(t)
*
* < xi(t2)x(t1) > = G delta (t2-t1)
*
**********************************************************************/
double dr_par_1k,vpar_1k,vpar_2k,eta_par;
// Wiener process propto sqrt(dt)
eta_par = XI_PAR_SQRT_DT_DIV_M * gsl_ran_gaussian_ziggurat(rand_vec,1.0);
// Langevin eq. in par direction // EXP_VPAR = exp(-DT_DIV_2*GAMMA/M);
vpar_1k = vpar[tstep-1]*EXP_VPAR; dr_par_1k = DT_DIV_2*vpar_1k; //rpar_1k = rpar[i-1] + DT_DIV_2*vpar_1k;
vpar_2k = vpar_1k + eta_par;
vpar[tstep] = vpar_2k*EXP_VPAR; dr_par[tstep] = dr_par_1k + DT_DIV_2*vpar_2k; //rpar[i] = rpar_1k + DT_DIV_2*vpar_2k;
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void dynamics_r_perpendicular(int tstep)
{
/**
// Overdamped langevin eq. in perp direction
dr_perp[i] = eta_perp; //rperp[i] += eta_perp;
rB[i] += eta_perp;
vperp[i] = INV_DT*eta_perp;
*/
dr_perp[tstep] = SQRT_Q*sin(d_theta[tstep]);
//dr_perp[tstep] = SQRT_Q*d_theta[tstep]; // Does not change aparently
return;
}
/************************************************************************************************
* *
************************************************************************************************/
double wrap_angle(double theta)
{
return theta - two_PI*floor(theta/two_PI);
}
/************************************************************************************************
* *
************************************************************************************************/
void dynamics_theta(int tstep)
{
// Overdamped langevin eq. in THETA
double eta_theta;
eta_theta = XI_THETA_SQRT_DT * gsl_ran_gaussian_ziggurat(rand_vec,1.0);
d_theta[tstep] = eta_theta;
theta[tstep] = theta[tstep-1] + eta_theta;
theta[tstep] = wrap_angle(theta[tstep]);
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void dynamics(int tstep)
{
double sin_alpha,cos_alpha;
double dr,dr2;
double cos_theta_old,sin_theta_old,cos_theta_dr,sin_theta_dr;
dynamics_r_parallel(tstep);
cos_theta_old = cos(theta[tstep-1]);
sin_theta_old = sin(theta[tstep-1]);
dynamics_theta(tstep);
vpar[tstep] *= cos(d_theta[tstep]);
dynamics_r_perpendicular(tstep);
//Find total displacement
dr2 = dr_par[tstep]*dr_par[tstep] + dr_perp[tstep]*dr_perp[tstep];
dr = sqrt(dr2);
// Find displacement direction relative to original (old) direction (orientation)
if (dr != 0.0)
{
sin_alpha = dr_perp[tstep]/dr;
cos_alpha = dr_par[tstep] /dr;
}
else // Maintain direction (alpha = 0.0)
{
//fprintf(stderr,"=====>>> dr == 0.0\n");fflush(stderr);
sin_alpha = 0.0;
cos_alpha = 1.0;
}
// Find displacement angle relative to x-axis
// + is the counterclockwise direction: (theta_old + alpha)
cos_theta_dr = cos_theta_old*cos_alpha - sin_alpha*sin_theta_old;
sin_theta_dr = sin_theta_old*cos_alpha + sin_alpha*cos_theta_old;
dx[tstep] = dr*cos_theta_dr;
dy[tstep] = dr*sin_theta_dr;
rx[tstep] = rx[tstep-1] + dx[tstep];
ry[tstep] = ry[tstep-1] + dy[tstep];
// Find velocity
v2[tstep] = vpar[tstep]*vpar[tstep];
return;
}
Por fim, colocou-se a ordem de execução das funções na ordem correta e calculou-se os parâmetros termodinâmicos relevantes.
int main(int argc, char *argv[])
{
int npart,k;
unsigned long int t_counter;
if (TRANSIENT_STEPS > MAX_STEPS)
{
printf("Number of transient steps must be smaller than MAX_STEPS\n");
exit(1);
}
if (argc != 3)
{
printf("Program needs 2 arguments:\n 1) Value of N,\n 2) Value of K.\n");
exit(1);
}
N=atoi(argv[1]);
K=atof(argv[2]);
fprintf(stderr,"Setting constants... "); fflush(stderr);
set_constants();
fprintf(stderr,"Done\n"); fflush(stderr);
printf("Allocating pointers...\n");fflush(stdout);
allocate_pointers(MAX_STEPS);
set_correlation_vecs();
printf("Done: Allocating pointers\n");fflush(stdout);
set_gsl_rng();
printf("Done: Seting initial conditions.\n");fflush(stdout);
open_output_files();
printf("Done: Opening files.\n");fflush(stdout);
for(npart=0; npart<N; ++npart)
{
set_initial_conditions(MAX_STEPS);
for(t_counter=1;t_counter<TRANSIENT/DT;++t_counter)
dynamics(t_counter);
--t_counter; // == TRANSIENT_STEPS - 1 // fprintf(stderr,"Done transient.\n");fflush(stderr);
reset_initial_condition(t_counter);
//fprintf(stderr,"Done transient\n"); fflush(stderr);
for(t_counter=1;t_counter<MAX_STEPS;++t_counter)
dynamics(t_counter);
if (npart==0)
{
for(k=0;k<MAX_STEPS;++k)
fprintf(ftraj,"%f %e %e\n", k*DT, rx[k], ry[k]);
fclose(ftraj);
}
if (npart%10==0)
{
printf("Done particle %d dynamics. Calculating correlations... ", npart);
fflush(stdout);
}
calculate_correlations(rx,ry,vpar);
if (npart%10==0) printf("Done.\n");
}
print_correlations();
fclose(fcorr);
fclose(fr2);
//for(i=0;i<NUM_CORR_MEASURES;++i) printf("%ld\n",corr_time[i]);
printf("Freeing pointers\n");fflush(stdout);
free_pointers(MAX_STEPS);
return 0;
}
/************************************************************************************************
* *
************************************************************************************************/
void set_correlation_vecs()
{
int i;
for(i=0;i<NUM_CORR_MEASURES;++i)
{
r2[i] = 0.0;
v2_ave[i] = 0.0;
v_ave[i] = 0.0;
corr_v_ave[i] = 0.0;
}
for(i=0;i<NUM_VCORR_MEASURES;++i)
corr_v[i] = 0.0;
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void calculate_correlations(double *rx, double *ry, double *v)
{
double c_v, dr2, dx, dy, v_ave_temp,temp;
int i,j,k,num_points;
for(k=0; k<NUM_VCORR_MEASURES;++k)
{
i=k*STEP_SIZE_VCORR; //vcorr_time[k];
c_v = 0.0;
num_points = 0;
for (j=0; j < MAX_STEPS - i; ++j)
{
c_v += v[j+i] * v[j];
++num_points;
}
corr_v[k] += c_v/num_points;
//fprintf(stderr," Done corr delta t %f\n",i*DT);fflush(stderr);
}
//printf("Done 1\n");fflush(stdout);
//for (i=0; i < MAX_STEPS; ++i)
for(k=0; k<NUM_CORR_MEASURES;++k)
{
i=corr_time[k];
dr2 = 0.0;
v_ave_temp = 0.0;
v2_ave[k] += v[i]*v[i];
num_points = 0;
for (j=0; j < MAX_STEPS - i; ++j)
{
dx = rx[j+i]-rx[j];
dy = ry[j+i]-ry[j];
temp = dx*dx + dy*dy;
dr2 += temp; // dx*dx + dy*dy;
v_ave_temp += sqrt(temp)/(i*DT);
++num_points;
}
r2[k] += dr2/num_points;
v_ave[k] += v_ave_temp/num_points;
//fprintf(stderr," Done corr delta t %f\n",i*DT);fflush(stderr);
}
//printf("Done 2\n");fflush(stdout);
/*
* for(k=0; k<NUM_VCORR_MEASURES;++k)
{
i=corr_time[k];
c_v = 0.0;
num_points = 0;
for (j=0; j < MAX_STEPS - i; ++j)
{
c_v += v_ave[j+i] * v_ave[j];
++num_points;
}
corr_v_ave[k] += c_v/num_points;
//fprintf(stderr," Done corr delta t %f\n",i*DT);fflush(stderr);
}
*/
//printf("Done 3\n");fflush(stdout);
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void print_correlations(void)
{
int i,k;
double t;
//for(i=0;i<MAX_STEPS;++i)
for(k=0;k<NUM_VCORR_MEASURES;++k)
{
i=k*STEP_SIZE_VCORR;//vcorr_time[k];
t=i*DT;
corr_v[k] /= N;
fprintf(fcorr,"%f %e\n", t, corr_v[k]);
}
for(k=0;k<NUM_CORR_MEASURES;++k)
{
i=corr_time[k];
t=i*DT;
r2[k] /= N;
v2_ave[k] /= N;
v_ave[k] /= N;
corr_v_ave[k] /= N;
//fprintf(fr2,"%f %e %e %e %e %e\n", t, r2[k], msd_analitico (t), v2_ave[k], v_ave[k],corr_v_ave[k]);
fprintf(fr2,"%f %e %e %e %e\n", t, r2[k], msd_analitico (t), v2_ave[k], v_ave[k]);
}
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void set_initial_conditions(int N)
{
int i;
for (i=0;i<N;++i)
{
rx[i] = 0.0;
ry[i] = 0.0;
dr_par[i] = 0.0;
dr_perp[i] = 0.0;
vpar[i] = 0.0; //(G/(2*M2*(GAMMA_M+K))) * gsl_ran_gaussian_ziggurat(rand_vec,1.0);
v2[i] = 0.0; //vpar[i]*vpar[i]+vperp[i]*vperp[i];
theta[i] = 0.0; //two_PI*gsl_rng_uniform(rand_vec);
}
vpar[0] = (G/(2*M2*(GAMMA_M+K))) * gsl_ran_gaussian_ziggurat(rand_vec,1.0); //raiz, nao?!?!
//Isotropic Initial condition
//Choose a rand_vec with direction uniformly distributed in [0,2pi)
theta[0] = two_PI*gsl_rng_uniform(rand_vec);
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void reset_initial_condition(int t_counter)
{
rx[0] = 0.0; //rx[t_counter];
ry[0] = 0.0; //ry[t_counter];
dr_par[0] = dr_par[t_counter];
dr_perp[0] = dr_perp[t_counter];
theta[0] = theta[t_counter];
vpar[0] = vpar[t_counter];
v2[0] = v2[t_counter];
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void allocate_pointers(int n)
{
rx = create_double_pointer(n);
ry = create_double_pointer(n);
dx = create_double_pointer(n);
dy = create_double_pointer(n);
dr_par = create_double_pointer(n);
dr_perp = create_double_pointer(n);
vpar = create_double_pointer(n);
v2 = create_double_pointer(n);
theta = create_double_pointer(n);
d_theta = create_double_pointer(n);
r2 = create_double_pointer(NUM_CORR_MEASURES);
v2_ave = create_double_pointer(NUM_CORR_MEASURES);
corr_v = create_double_pointer(NUM_VCORR_MEASURES);
v_ave = create_double_pointer(NUM_CORR_MEASURES);
corr_v_ave = create_double_pointer(NUM_CORR_MEASURES);
return;
}
/************************************************************************************************
* *
************************************************************************************************/
void free_pointers(int n)
{
free(rx);
free(ry);
free(dx);
free(dy);
free(dr_par);
free(dr_perp);
free(vpar);
free(corr_v);
free(theta);
free(d_theta);
free(r2);
free(v2);
free(v2_ave);
free(v_ave);
free(corr_v_ave);
gsl_rng_free (rand_vec);
return;
}
/*********************************************************************
*** Time Table ***
*** The total number of time steps and the number of measures are ***
*** specified. ***
*********************************************************************/
void create_time_table(long *t1, int total_time, int measures)
{
unsigned long i,k;
double temp;
t1[0] = 0;
temp = pow((double) total_time,1.0/(measures-1));
k=0;
for (i=1; i<measures; ++i)
{
t1[i] = (int) pow(temp, (double) i);
if (t1[i]<=k) t1[i]=k+1;
k = t1[i];
}
t1[--i] = total_time-2;
return;
}











![{\displaystyle {\frac {d_{i}^{n}(t)}{dt}}={\frac {1}{\tau }}arcsin[(n_{i}(t){\frac {v_{i}(t)}{|v_{i}(t)|}})e_{z}]+\xi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e5655a8c3f515b003ca81221614704e523bb889)













p_{i}(t+\Delta t))p_{i}(t+\Delta t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2b19a64a7b87d6e0516194a6ceeb6651163c4fc)










![{\displaystyle [r_{\perp }(t+\Delta t)-r_{\perp }(t)]n_{i}(t)=n_{i}(t)\int _{t}^{t+\Delta t}\xi _{\perp }(t)dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1c8ffa1d2f99204a928af58440d2913ffd534f6)












![{\displaystyle <r^{2}>={\frac {4DP}{1-S}}[\tau -(1-S)(1-e^{-\tau })]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ea00b13505130fbf626604fd5285bac32c3bb7)