Fórmula de Lagrange

Polinômios de Lagrange

Baseado no fato de que sobre $N$ pontos $(X_{1},Y_{1}),(X_{2},Y_{2}),\cdots ,(X_{N},Y_{N})$ passa um único polinômio de grau $N-1$, o Polinômio de Lagrange pode ser usado como fórmula de interpolação ou extrapolação:

$P(x)=\sum _{i=1}^{N}Y_{i}L_{i}(x)$

onde

$L_{i}(x)=\prod _{j=1,j\neq i}^{N}{\frac {x-X_{j}}{X_{i}-X_{j}}}={\frac {x-X_{1}}{X_{i}-X_{1}}}\cdots {\frac {x-X_{i-1}}{X_{i}-X_{i-1}}}{\frac {x-X_{i+1}}{X_{i}-X_{i+1}}}\cdots {\frac {x-X_{N}}{X_{i}-X_{N}}}$

é um polinômio de grau $\;N-1$ em $\;x$. Tendo em vista que $L_{i}(X_{j})=\delta _{i,j}\;,$ onde o delta de Kronecker

$\delta _{ij}=\left\{{\begin{matrix}1,&{\mbox{se }}i=j\\0,&{\mbox{se }}i\neq j\end{matrix}}\right.$

é fácil verificar que, de fato,$\;P(X_{i})=Y_{i}$. Assim,$\;P(x)$ pode ser empregado para se estimar o valor de $\;Y(x)$ em pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;x} não tabulados.

Exemplo 1

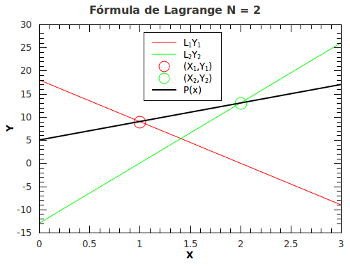
Fórmula de Lagrange para N=2.

Para exemplificar a fórmula de Lagrange, consideramos primeiramente uma reta que passa pelos pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_1,Y_1) = (1,9)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_2,Y_2) = (2,13)} , tendo assim Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 2} . Aplicando a fórmula de Lagrange, temos

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1 = \frac{x-X_2}{X_1-X_2} = \frac{x-2}{1-2} = -(x-2)}

e

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2 = \frac{x-X_1}{X_2-X_1} = \frac{x-1}{2-1} = (x-1)} ,

assim, o polinômio de Lagrange que passa pelos pontos desejados é dado por:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)=\sum_{i=1}^N Y_i L_i(x) = Y_1L_1 + Y_2L_2 = 9(-x+2) + 13(x-1) = 4x + 5 } .

Note que substituindo na equação acima, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(1) = 9} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(2) = 13} .

Exemplo 2

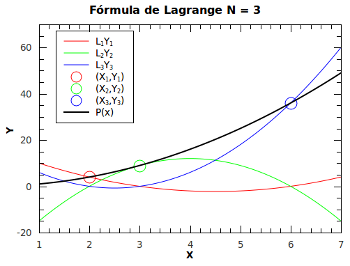
Fórmula de Lagrange para N=3.

Verificando a fórmula de Lagrange para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 3} . Suponhamos que desejamos encontrar qual é o polinômio que passa pelos pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_1,Y_1) = (2,4)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_2,Y_2) = (3,9)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_3,Y_3) = (6,36)} . Temos que:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1 = \left(\frac{x-X_2}{X_1-X_2}\right) \left(\frac{x-X_3}{X_1-X_3}\right) = \left(\frac{x-3}{2-3}\right) \left(\frac{x-6}{2-6}\right) = \frac{x^2-9x+18}{4}} ,

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2 = \left(\frac{x-X_1}{X_2-X_1}\right) \left(\frac{x-X_3}{X_2-X_3}\right) = \left(\frac{x-2}{3-2}\right) \left(\frac{x-6}{3-6}\right) = -\frac{x^2-8x+12}{3}}

e

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_3 = \left(\frac{x-X_1}{X_3-X_1}\right) \left(\frac{x-X_2}{X_3-X_2}\right) = \left(\frac{x-2}{6-2}\right) \left(\frac{x-3}{6-3}\right) = \frac{x^2-5x+6}{12}} ,

assim

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)=\sum_{i=1}^N Y_i L_i(x) = Y_1L_1 + Y_2L_2 + Y_3L_3 = 4\frac{x^2-9x+18}{4} - 9\frac{x^2-8x+12}{3} + 36\frac{x^2-5x+6}{12} = x^2 } .

Exemplo 3

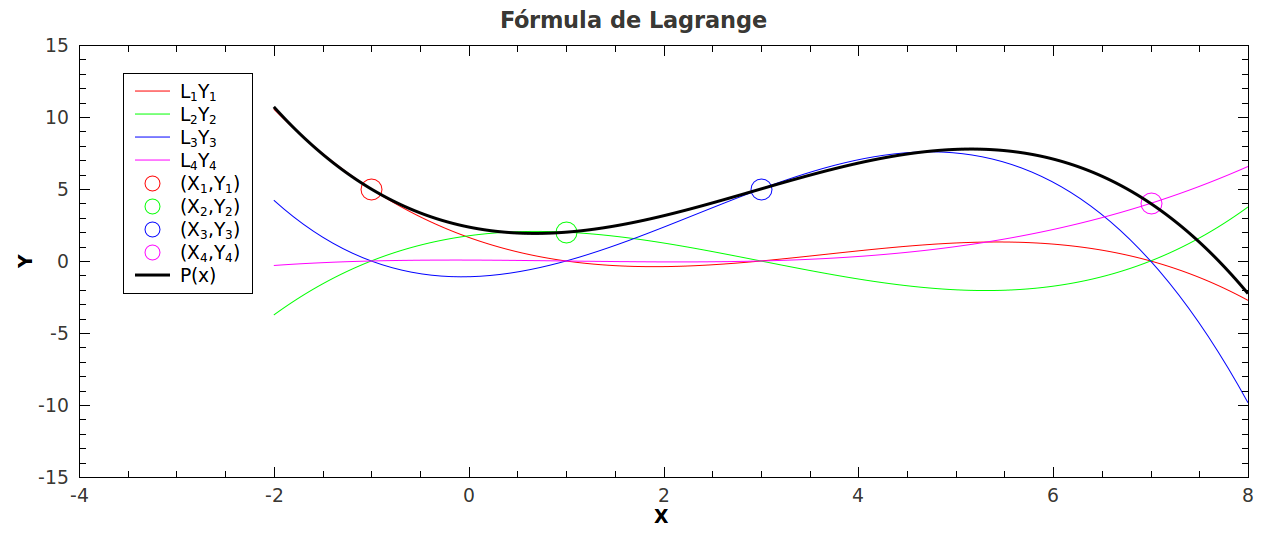
Para ilustrar graficamente o método da fórmula de Lagrange, usaremos um exemplo com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=4} . Considerando os quatro pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_1,Y_1) = (-1,5)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_2,Y_3) = (1,2)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_3,Y_3) = (-3,5)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_4,Y_4) = (7,4)} , as equações Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_i} ficam

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1 = -\frac{1}{64}(x^3-11x^2+31x-21)} ,

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2 = \frac{1}{24}(x^3-9x^2+11x+21)} ,

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_3 = -\frac{1}{32}(x^3-7x^2-x+7)}

e

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_4 = \frac{1}{192}(x^3-3x^2-x+3)} .

O gráfico abaixo mostra os quatro pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_i,Y_i)} , as curvas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_iY_i} e a curva final Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)} . Lembre-se que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)} é a curva gerada pela soma dos polinômios Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_iY_i} . Note que a curva Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1Y_1} passa pelo ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_1,Y_1)} , assim como as demais e a curva Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)} passa por todos os pontos.

Numericamente

Na prática, a implementação numérica do polinômio de Lagrange é complicada. Computacionalmente não é possível fazer um programa geral para interpolação de ordem arbitrária, isto é fazer um programa que, com os N pontos de entrada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {X_i,Y_i}} , devolva um polinômio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)} interpolador de grau N. Isto envolve computação simbólica (do tipo utilizada em programas proprietários como o Mathematica, Maple, ou livres como Maxima). Por outro lado a implementação numérica do método na força bruta envolve um duplo laço de ordem N: devem ser somados N termos (os Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_i(x)} ) onde cada um deles é construído como um produto de N-1 termos; ao todo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^2} cálculos para cada ponto x (isto fica como exercício a partir da fórmula geral do Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)} ).

O Algoritmo de Neville [1], Implementação do algoritmo de Neville, é muito útil na realização desta tarefa.Ao final, veremos que o polinômio interpolador de grau n pode ser reconstruído com polinômios de grau n-1. Este processo gera uma fórmula de recorrência, que é um recurso bastante comum em algoritmos computacionais.

Para deduzirmos esta fórmula de recorrência, começamos aproximando cada intervalo por um valor constante. Podemos representar esta aproximação por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_1(x)=Y_1,\; P_2(x)=Y_2,\; \cdots\,\; P_N(x)=Y_N} . Melhorando a descrição, empregando agora uma aproximação linear em cada intervalo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [X_i,\;X_{i+1}]} , denotamos por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{12}(x),\;P_{23}(x),\; \cdots,\; P_{N-1,N}(x)} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i,i+1}(x)\;} é o polinômio que passa exatamente sobre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_i,Y_i)\;} eFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;(X_{i+1},Y_{i+1})} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i,i+1}(x)=\frac{x-X_{i+1}}{X_i-X_{i+1}}Y_i+\frac{x-X_i}{X_{i+1}-X_i}Y_{i+1}\;. }

Vemos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i, i+1}(x)\;} pode ser escrito como:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i,i+1}(x)=\frac{(x-X_{i+1})P_i(x)-(x-X_i)P_{i+1}(x)}{X_i-X_{i+1}} }

Isto sugere que há uma relação entre os polinômios de ordem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;n} com os de ordem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;n+1} . Para verificar isto, vamos considerar, agora, uma parábola passando exatamente sobre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_i,Y_i)\;,(X_{i+1},Y_{i+1})} eFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;(X_{i+2},Y_{i+2})} , que denotaremos por,Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;P_{i,i+1,i+2}(x)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i,i+1,i+2}(x)=\frac{x-X_{i+1}}{X_i-X_{i+1}}\frac{x-X_{i+2}}{X_i -X_{i+2}}Y_i +\frac{x-X_i}{X_{i+1}-X_i}\frac{x-X_{i+2}}{X_{i+1}-X_{i+2}}Y_{i+1} +\frac{x-X_i}{X_{i+2}-X_i}\frac{x-X_{i+1}}{X_{i+2}-X_{i+1}}Y_{i+2} }

Fatorando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;1/(X_i-X_{i+2})} e somando e subtraindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x-X_i}{X_{i+1}-X_i}(x-X_{i+2})Y_{i+1}} , obtemos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i,i+1,i+2}(x) =\frac{1}{X_i-X_{i+2}}\left[(x-X_{i+2})P_{i,i+1}(x) -F(x)\right] }

onde

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x)=(x-X_i)\left[\frac{x-X_{i+1}}{X_{i+2}-X_{i+1}}Y_{i+2} -\frac{X_i-X_{i+2}}{X_{i+1}-X_i}\frac{x-X_{i+2}}{X_{i+1}-X_{i+2}}Y_{i+1} +\frac{x-X_{i+2}}{X_{i+1}-X_i}Y_{i+1}\right]\;. }

Note que o último termo desta expressão corresponde àquele que foi subtraído após seu termo de sinal contrário ter sido somado à expressão que levou aFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;P_{i,i+1}(x)} na equação paraFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;P_{i,i+1,i+2}(x)} . Rearranjando os termos acima, encontramos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x)=(x-X_i)\left[\frac{x-X_{i+2}}{X_{i+1}-X_{i+2}}Y_{i+1}+\frac{x-X_{i+1}}{X_{i+2}-X_{i+1}}Y_{i+2}\right] =(x-X_i)P_{i+1,i+2}(x)\;. }

Substituindo este resultado na equação paraFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;P_{i,i+1,i+2}(x)} , obtemos finalmente:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i,i+1,i+2}(x) =\frac{1}{X_i-X_{i+2}}\left[(x-X_{i+2})P_{i,i+1}(x) -(x-X_i)P_{i+1,i+2}(x)\right] }

Assim, notamos que, de fato, há uma relação de recorrência bastante simples entre os polinômios que envolvem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;n} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;n+1} pontos, cuja forma geral é dada por:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i,i+1,\cdots,i+k}(x) =\frac{1}{X_i-X_{i+k}}\left[(x-X_{i+k})P_{i,i+1,\cdots,i+k-1}(x) -(x-X_i)P_{i+1,i+2,\cdots,i+k}(x)\right] }

Por ser muito mais simples de se implementar numericamente do que a expressão original para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;P(x)} , é esta relação de recorrência que é, de fato, utilizada em cálculos numéricos. Os erros cometidos podem ser estimados calculando-se as diferenças entre as diferentes ordens do polinômio:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{(1)}_{k,i}(x)=P_{i,i+1,\cdots,i+k}(x)-P_{i,i+1,\cdots,i+k-1}(x) }

e

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{(2)}_{k,i}(x)=P_{i,i+1,\cdots,i+k}(x)-P_{i+1,i+2,\cdots,i+k}(x)\;. }

Ao invés de se gerar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;P(x)} a partir da relação de recorrência para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{i,i+1,\cdots,i+k}(x)} , pode-se utilizar as equações acima e obter relações de recorrência para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;D^{(1)} \mbox{ e } D^{(2)}} . No final, obtemos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;P(x)} a partir destas quantidades. Este desenvolvimento é deixado como exercício.

É importante notar que em nenhum ponto da discussão foi evocada a necessidade dos pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\{X_i\}} serem igualmente espaçados. Portanto, as fórmulas apresentadas aqui podem ser aplicadas em situações bastante gerais.

---

Como discutido na seção Interpolação e extrapolação, é desaconselhável o uso de polinômios de grau elevado. Por isto, apenas um pequeno subconjunto dos valores tabulados, nas vizinhanças do ponto de interesse Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;X} , deve ser empregado. Por exemplo, digamos que temos uma tabela com 100 pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\{(X_i,Y_i)\}} . Se desejamos estimar o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;Y} no interior da região Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [X_1,\; X_N]} , ao invés de construir um polinômio de grau 99, podemos, por exemplo, dividir o espaço em 25 sub-regiões e usar polinômios cúbicos em cada uma delas, utilizando apenas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_{i-1},Y_{i-1}),\; (X_i,Y_i),\; (X_{i+1},Y_{i+1})} eFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;(X_{i+2},Y_{i+2})} .

Contudo, devemos notar que, embora a interpolação seja contínua nas interfaces das regiões, a continuidade das derivadas 1^a e 2^a não é garantida. Em situações em que estas propriedades importam, outras aproximações devem ser adotadas (veja, por exemplo, Spline cúbico).

---