Modelo espacialmente explícito: mudanças entre as edições
(Criou página com '{{Ecologia| Modelo de Lotka-Volterra amortecido | - }} {{Ecologia| Modelo de Lotka-Volterra amortecido | - }}') |
Sem resumo de edição |
||
| (9 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[Modelo de | {{Ecologia| [[Modelo de Levins aprimorado para 3 espécies]] | - }} | ||
=== Características === | |||
{{Ecologia| [[Modelo de | O modelo foi construído para ser coerente com o [[contexto]] ecológico da região norte da patagônia. | ||
*<math display="inline">L\times L</math> fragmentos que pode estar destruídos, vagos ou ocupados (por uma ou mais espécies): | |||
*<math display="inline">x_{i}\rightarrow</math> denota a fração de fragmentos ocupados por herbívoros da espécie <math display="inline">i</math> (<math display="inline">1:</math> guanaco, <math display="inline">2:</math> ovelha); | |||
*<math display="inline">y\rightarrow</math> fração ocupada por predadores; | |||
*Tempo avança discretamente e os seguintes passos ocorrem de forma síncrona: | |||
**'''Colonização''': um fragmento disponível pode ser colonizado pela espécie <math display="inline">\alpha\in\left\{ x_{1},x_{2},y\right\}</math> por um fragmento como primeiro vizinho ocupado, com probabilidade de colonização <math display="inline">c_{\alpha}</math> | |||
**'''Extinção''': Um fragmento ocupado pode se tornar vago pela espécie <math display="inline">\alpha</math> por probabilidade de extinção local <math display="inline">e_{\alpha}</math> | |||
***'''Predação''': Um fragmento que é ocupado tanto por presa quanto um predador, tem uma probabilidade de extinção da presa, dada por uma probabilidade <math display="inline">\mu_{\alpha}</math> (<math display="inline">\mu_{y}=0</math>). Neste caso então é utilizado a probabilidade de extinção local (<math>e_\alpha+\mu_\alpha </math>), ou seja, consideramos como eventos mutuamente exclusivos. | |||
**'''Deslocamento competitivo''': Um fragmento ocupado por ambos herbívoros, pode ser liberado do herbívoro inferior (<math display="inline">x_{2}</math>) com probabilidade <math display="inline">c_{x_{1}}</math>. | |||
Se temos <math display="inline">n</math> vizinhos ocupados na vizinhança de um fragmento disponível para a colonização, a probabilidade de ser colonizado por qualquer um dos vizinhos é dado por: | |||
<math display="block">p_{\alpha}=1-\left(1-c_{\alpha}\right)^{n}</math>Uma vez que <math display="inline">b_{\alpha}=\left(1-c_{\alpha}\right)</math> é a probabilidade de que <math display="inline">\alpha</math> não colonize o fragmento. Como são eventos independentes a probabilidade de não colonizar tendo 4 vizinhos ocupados por exemplo, seria: <math display="inline">b_{\alpha}b_{\alpha}b_{\alpha}b_{\alpha}=b_{\alpha}^{4}</math>, logo a probabilidade de colonizar é dada por <math display="inline">p_{\alpha}=1-b_{\alpha}^{4}</math>. A dinâmica do modelo é estudada através de uma simulação computacional realizada em um sistema fechado por barreiras impenetráveis, isto é, o perímetro é composto por fragmentos destruídos, então a grade tem tamanho <math display="inline">L+2\times L+2</math>. O algoritmo pode ser sintetizado nos seguintes passos: | |||
#Definir os parâmetros do modelo; | |||
#Destruir a fração <math display="inline">D</math> de fragmentos; | |||
#Distribuir a população inicial: | |||
#*Cada herbívoro ocupa 50% dos fragmentos disponíveis. | |||
#*O predador ocupa 50% dos fragmentos ocupados por herbívoros. | |||
#O sistema evolui de forma síncrona seguindo regras estocástica e os eventos discutidos anteriormente; | |||
#O sistema evolui durante um transiente (por volta de 3000 passos) até que a flutuação nas populações se estabilize; | |||
#Média temporal: é realizada então a média temporal (tipicamente ao longo dos últimos 2000 passos da atual simulação) da fração de fragmentos ocupados por cada espécie na atua simulação. | |||
#Média do ensemble: São realizadas nova simulações (tipicamente 100) com os mesmos parâmetros, e então é calculado médias do conjunto das frações ocupadas por cada espécie. | |||
Um ensemble nada mais é que uma idealização consistindo de um largo número de cópias mentais de um sistema, onde cada uma destas cópias corresponde a um possível estado que o sistema pode estar. Basicamente uma coleção onde todas cópias possuem as mesmas propriedades, porém em estados diferentes<ref>[https://ocw.mit.edu/courses/physics/8-08-statistical-physics-ii-spring-2005/lecture-notes/microcanonical_en.pdf Statistical Ensembles] (Instituto de Tecnologia de Massachusetts)</ref>. Dessa forma, enquanto uma média temporal (ou espacial) é a quantidade média de uma certa quantidade de um único sistema em um certo intervalo de tempo (ou espaço), a média do ensemble é quantidade média de uma certa quantidade entre muitos sistemas idênticas em um certo momento no tempo (ou espaço)<ref>[https://www.nii.ac.jp/qis/first-quantum/e/forStudents/lecture/pdf/noise/chapter1.pdf Mathematical Methods] (Yoshihisa Yamamoto, Instituto Nacional de Informática)</ref>. | |||
====Controle de predação==== | |||
Foi analisado o sistema em diferentes cenários buscando entender a dependência do estado do sistema para diferentes probabilidades de extinção de predadores e destruição do habitat. Estes parâmetros foram escolhidos pois tem origem antropogênicas. A primeira análise analisamos a a controle de predação, varia-se a probabilidade de extinção do predador (<math display="inline">e_{y}</math>) para obter a fração ocupada pelas três espécies após o sistema estar em equilíbrio. Os parâmetros são: | |||
*<math display="inline">D=0.3</math> | |||
*<math display="inline">c_{x_{2}}=0.1>c_{x_{1}}=0.05</math> | |||
*<math display="inline">e_{x_{2}}=0.01<e_{x_{1}}=0.05</math> | |||
*<math display="inline">\mu_{x_{2}}=0.8\gg\mu_{x_{1}}=0.2</math> | |||
*<math display="inline">c_{y}=0.015</math> | |||
*<math display="inline">L=100</math> | |||
Além disso, para cada valor de <math display="inline">e_{y}</math> a simulação tem a duração de 5000 passos e é calculada então a média temporal de simulação para os últimos 2000 passos. É executado 100 simulações para cada valor de <math>e_y</math> e então é obtido a média do ensemble. | |||
===Destruição do habitat=== | |||
A segunda análise é inspirada nos três cenários discutido no [[contexto]]. cada cenário é identificado por um fração diferente de destruição do habitat: | |||
*Baixo conflito: <math display="inline">D=0.1</math> | |||
*Médio conflito: <math display="inline">D=0.3</math> | |||
*Alto conflito: <math display="inline">D=0.5</math> | |||
Para baixo e alto conflito é executado uma simulação de 9000 passos enquanto para médio conflito é executado de 18000 passos. Porém todas compartilham do fator em comum que as ovelhas são retiradas no passo <math display="inline">5000</math> e então é realizado a seguinte alteração de parâmetros para reiniciar a simulação: | |||
*<math display="inline">c_{x_{1}}=0.05\rightarrow0.1</math> | |||
*<math display="inline">e_{x_{1}}=0.05\rightarrow0.025</math> | |||
*<math display="inline">e_{y}=0.02\rightarrow0.015</math> | |||
*<math display="inline">\mu_{x_{1}}=0.2\rightarrow0.3</math> | |||
Vale destacar que aqui as simulações são executadas para um valor fixo de <math display="inline">e_{y}</math>, e que com o reinicio da simulação, as espécies apesar de manterem a mesma fração ocupada, acabam sendo redistribuídas aleatoriamente pelo habitat. | |||
===Resultados=== | |||
Primeiro vamos comparando resultado da simulação do código disponível abaixo com os dados originais: | |||
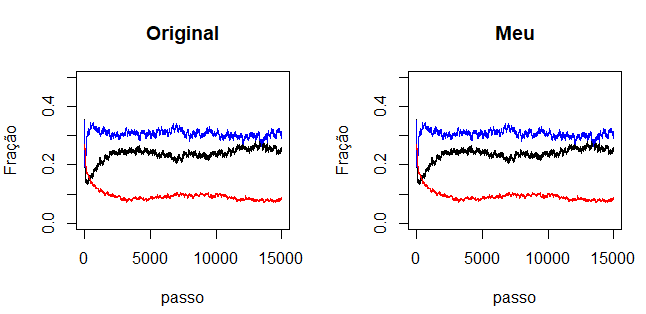
<div class="center">[[Ficheiro:comparacao.png|centro|miniaturadaimagem|Comparação entre os dados originais e os gerados pelo código em Python para uma evolução temporal com <math>e_y=0.017</math>.|alt=|646x314px]] | |||
</div> | |||
O módulo da diferença entre a fração final ocupada por cada espécie do código em Python e os dados originais foram: | |||
*<math display="inline">\left|\Delta x_{1}\right|=3.22\times10^{-8}</math> | |||
*<math display="inline">\left|\Delta x_{2}\right|=9.12\times10^{-9}</math> | |||
*<math display="inline">\left|\Delta y\right|=1.15\times10^{-9}</math> | |||
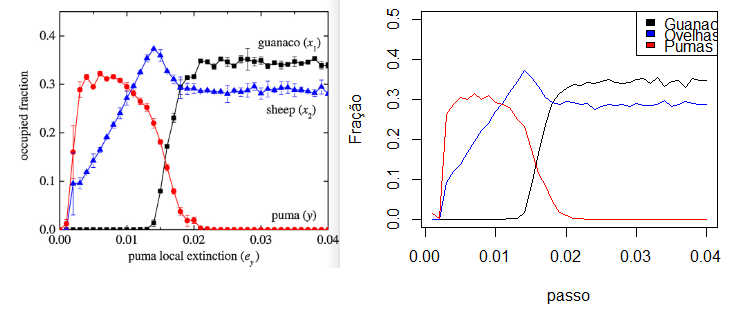
Variando então a taxa de extinção local dos pumas (<math display="inline">e_{y}</math>) para e calculando as médias dos ensembles temos: | |||
[[Ficheiro:media_esemble.png|centro|miniaturadaimagem|729x318px|A esquerda o gráfico retirado do artigo, e a direita o gerado em Python. ]] | |||
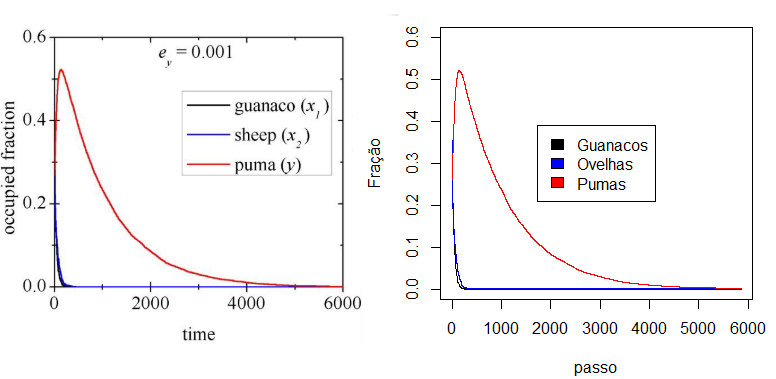
Porém devido à limitação de recursos computacionais, foi executado apenas 1 vez a simulação com cada valor <math>e_y</math>. Além disso foi reproduzido o cenário para <math display="inline">e_{y}=0.001</math>. | |||
[[Ficheiro:0001.png|centro|miniaturadaimagem|614x300px|A esquerda o gráfico retirado do artigo, e a direita o gerado em Python. ]] | |||
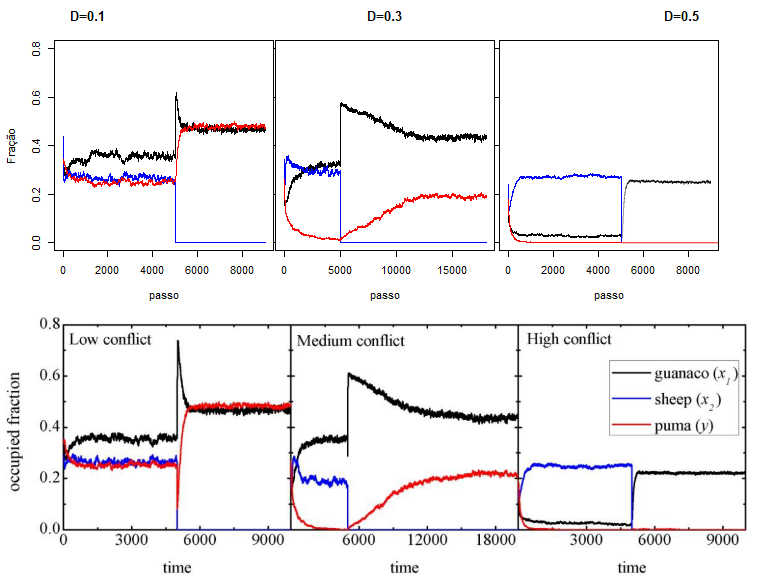
Conforme discutido, também foi simulado o cenário de conflitos:<div class="center">[[Ficheiro:conflitos.png|centro|miniaturadaimagem|397x300px|as três imagens superiores se referem aos gráficos gerados via Python e as inferiores ás originais do artigo.]] | |||
</div> | |||
<div align="center"> | |||
{| class="wikitable" | |||
| align="center" |Espécie | |||
| align="center" |Baixo conflito | |||
| align="center" | | |||
| align="center" |Médio Conflito | |||
| align="center" | | |||
| align="center" | Alto Conflito | |||
| align="center" | | |||
|- | |||
| align="center" | | |||
| align="center" |Artigo | |||
| align="center" |Meu | |||
| align="center" |Artigo | |||
| align="center" | Meu | |||
| align="center" | Artigo | |||
| align="center" |Meu | |||
|- | |||
| align="center" |Guanaco (<math display="inline">x_{1}</math>) | |||
| align="center" |<math display="inline">0.35\rightarrow0.47</math> | |||
| align="center" |<math display="inline">0.34\rightarrow0.47</math> | |||
| align="center" |<math display="inline">0.32\rightarrow0.45</math> | |||
| align="center" |<math display="inline">0.31\rightarrow0.44</math> | |||
| align="center" |<math display="inline">0.03\rightarrow0.20</math> | |||
| align="center" |<math display="inline">0.02\rightarrow0.18</math> | |||
|- | |||
| align="center" | Ovelha (<math display="inline">x_{2}</math>) | |||
| align="center" |<math display="inline">0.26\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.24\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.29\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.29\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.29\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.27\rightarrow0.00</math> | |||
|- | |||
| align="center" |Puma (<math display="inline">y</math>) | |||
| align="center" |<math display="inline">0.25\rightarrow0.48</math> | |||
| align="center" |<math display="inline">0.25\rightarrow0.47</math> | |||
| align="center" |<math display="inline">0.02\rightarrow0.17</math> | |||
| align="center" |<math display="inline">0.01\rightarrow0.19</math> | |||
| align="center" |<math display="inline">0.00\rightarrow<0.01</math> | |||
| align="center" |<math display="inline">0.00\rightarrow0.00</math> | |||
|} | |||
</div> | |||
=== Códigos=== | |||
O seguinte código em fortran foi utilizado para gerar os números pseudo-aleatórios:<pre> | |||
! Gerador de números pseudo-aleatórios | |||
! Jhordan Silveira de Borba | |||
! sbjhordan@gmail.com | |||
program mytest1 | |||
real RAN2 | |||
EXTERNAL RAN2 | |||
IDUM= -135 | |||
open (unit=1,file="psd.dat") | |||
DO i=1,2000000000 | |||
write(1,*),real(RAN2(IDUM)) | |||
!print *,i | |||
END DO | |||
close(1) | |||
end | |||
FUNCTION RAN2(IDUM) | |||
PARAMETER (M=714025,IA=1366,IC=150889,RM=1.4005112E-6) | |||
DIMENSION IR(97) | |||
save IR, IY | |||
DATA IFF /0/ | |||
IF(IDUM.LT.0.OR.IFF.EQ.0)THEN | |||
IFF=1 | |||
IDUM=MOD(IC-IDUM,M) | |||
DO J=1,97 | |||
IDUM=MOD(IA*IDUM+IC,M) | |||
IR(J)=IDUM | |||
END DO | |||
IDUM=MOD(IA*IDUM+IC,M) | |||
IY=IDUM | |||
ENDIF | |||
J=1+(97*IY)/M | |||
IF(J.GT.97.OR.J.LT.1)PAUSE | |||
IY=IR(J) | |||
RAN2=IY*RM | |||
IDUM=MOD(IA*IDUM+IC,M) | |||
IR(J)=IDUM | |||
RETURN | |||
END | |||
</pre>E o seguinte código base em Python é responsável pela simulação: | |||
# -*- coding: UTF-8 -*- | |||
# Modelo espacialmente explícito | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
#Bibliotecas | |||
import numpy as np # Biblioteca de funções matemáticas | |||
import copy # Biblioteca com funções para copiar | |||
#CONDIÇÕES INICIAIS ------------------------------------------------------ | |||
maxt = 15000 #tiempo total de cada realizacion | |||
Lx = 100 #tamaño del sustrato | |||
Ly = 100 | |||
#Fracciones iniciales | |||
D = 0.3 #fraccion inicial de sitios destruidos | |||
x10 = 0.5 #fraccion inicial de sitios ocupados por x1 | |||
x20 = 0.5 #fraccion inicial de sitios ocupados por x2 | |||
y0 = 0.5 #fraccion inicial de sitios ocupados por y | |||
#Tasas | |||
cx1 = 0.05 #colonizaciones | |||
cx2 = 0.1 | |||
cy = 0.015 | |||
ex1 = 0.05 #extinciones | |||
ex2 = 0.01 | |||
ey = 0.017 | |||
mx1y = 0.2 #depredaciones | |||
mx2y = 0.8 | |||
depx1 = ex1+mx1y #mortalidad aumentada=extincion+depredacion | |||
depx2 = ex2+mx2y | |||
g = open("psd.dat", "r") | |||
#Inicializaciones | |||
s = np.full((Lx, Ly), [1]) #matriz de habitat (1=sitio disponible, 0=destruido) | |||
x1 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio | |||
x2 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio | |||
y = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio | |||
for i in range(1,Lx-1): | |||
for j in range (1,Ly-1): | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < D): s[i,j]=0 | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < x10 and s[i,j]==1): x1[i,j]=1 | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < x20 and s[i,j]==1): x2[i,j]=1 | |||
rnd=float(g.readline())#np.random.rand() | |||
if ((x1[i,j]==1 or x2[i,j]==1) and rnd < y0): y[i,j]=1 | |||
for i in range(Lx): #destruimos los bordes del habitat | |||
s[i,0]=0 | |||
s[i,Ly-1]=0 | |||
for j in range(Ly): | |||
s[0,j]=0 | |||
s[Lx-1,j]=0 | |||
#------------------------------------------------------- | |||
#Lazo temporal | |||
fx1=sum(sum(x1))/((Lx-2)*(Ly-2)) | |||
fx2=sum(sum(x2))/((Lx-2)*(Ly-2)) | |||
fy =sum(sum(y)) /((Lx-2)*(Ly-2)) | |||
f = open("minha.dat", "w") | |||
f.write(" "+str(0)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n") | |||
for it in range(maxt): | |||
if (float(it)%(float(maxt)/100)==0.): | |||
print("Porcentagem: "+str(it*100/maxt)) # Exibe o passo atual | |||
x1old=copy.copy(x1) #poblaciones del paso anterior | |||
x2old=copy.copy(x2) | |||
yold=copy.copy(y) | |||
#Recorro la malla | |||
for i in range (1,Lx-1): | |||
for j in range (1,Ly-1): | |||
#colonizaciones | |||
if (x1old[i,j]==0 and s[i,j]==1): #colonizacion de x1 si el sitio esta libre de x1 y no destruido: | |||
nvec=x1old[i-1,j]+x1old[i+1,j]+x1old[i,j-1]++x1old[i,j+1] #cantidad de vecinos ocupados | |||
p=1.0-(1.0-cx1)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < p):x1[i,j]=1 | |||
if (x2old[i,j]==0 and s[i,j]==1 and x1old[i,j]==0): #colonizacion de x2 si el sitio esta libre de x1 y x2, y no destruido: | |||
nvec=x2old[i-1,j]+x2old[i+1,j]+x2old[i,j-1]+x2old[i,j+1] #cantidad de vecinos ocupados | |||
p=1.0-(1.0-cx2)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < p): x2[i,j]=1 | |||
ocup=0 #ocupacion de herbivoros | |||
if (x1old[i,j]==1 or x2old[i,j]==1): ocup=1 | |||
if (yold[i,j]==0 and ocup==1): #colonizacion de y si el sitio está libre de y,y ocupado por un x | |||
nvec=yold[i-1,j]+yold[i+1,j]+yold[i,j-1]+yold[i,j+1] #cantidad de vecinos ocupados | |||
p=1.0-(1.0-cy)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < p): y[i,j]=1 | |||
#extinciones sin depredadores | |||
if (x1old[i,j]==1 and yold[i,j]==0): #extincion de x1 si el sitio esta ocupado | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < ex1): x1[i,j]=0 | |||
if (x2old[i,j]==1 and yold[i,j]==0): #extincion de x2 si el sitio esta ocupado | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < ex2): x2[i,j]=0 | |||
if (yold[i,j]==1): #extincion de y si el sitio esta ocupado | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < ey): y[i,j]=0 | |||
#depredacion (extinción de presas donde hay depredadores) | |||
if (x1old[i,j]==1 and yold[i,j]==1): #depredacion de y sobre x1 | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < depx1): x1[i,j]=0 | |||
if (x2old[i,j]==1 and yold[i,j]==1): #depredacion de y sobre x2 | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < depx2): x2[i,j]=0 | |||
#desplazamiento por competencia (jerarquia) | |||
if (x1old[i,j]==1 and x2old[i,j]==1): | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < cx1): x2[i,j]=0 | |||
fx1=sum(sum(x1))/((Lx-2)*(Ly-2)) | |||
fx2=sum(sum(x2))/((Lx-2)*(Ly-2)) | |||
fy =sum(sum(y)) /((Lx-2)*(Ly-2)) | |||
f.write(" "+str(it+1)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n") | |||
f.close | |||
g.close() | |||
Além disso, foi usado o script em R para gerar os gráficos comparando dois conjunto de dados, este script é facilmente editável pra exibir o resultado de apenas uma simulação:<pre> | |||
# Visualização de gráficos | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
Dados0 <- read.table("Endereço do arquivo 0") | |||
Dados1 <- read.table("Endereço do arquivo 1") | |||
par(mfrow=c(1,2)) | |||
plot( c(Dados0[,1]), c(Dados0[,2]), col="black", main="Original", ylab="Fração", xlab="passo" ,type="l",ylim=c(0,0.5)) | |||
lines(c(Dados0[,1]), c(Dados0[,3]), col="blue") | |||
lines(c(Dados0[,1]), c(Dados0[,4]), col="red") | |||
legend("topright", c("Guanacos","Ovelhas","Pumas"), fill=c("black","blue","red")) | |||
plot( c(Dados1[,1]), c(Dados1[,2]), col="black", main="Meu", ylab="Fração", xlab="passo" ,type="l",ylim=c(0,0.5)) | |||
lines(c(Dados1[,1]), c(Dados1[,3]), col="blue") | |||
lines(c(Dados1[,1]), c(Dados1[,4]), col="red") | |||
legend("topright", c("Guanacos","Ovelhas","Pumas"), fill=c("black","blue","red")) | |||
</pre> | |||
===Principal material utilizado=== | |||
#[https://arxiv.org/pdf/1409.0024.pdf Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances] (Fabiana Laguna e outros, Ecological Modelling) | |||
===Referências=== | |||
<references /> | |||
{{Ecologia| [[Modelo de Levins aprimorado para 3 espécies]] | - }} | |||
Edição atual tal como às 19h45min de 13 de abril de 2021
Anterior: Modelo de Levins aprimorado para 3 espécies | Índice: Ecologia | Próximo: -
Características
O modelo foi construído para ser coerente com o contexto ecológico da região norte da patagônia.
- fragmentos que pode estar destruídos, vagos ou ocupados (por uma ou mais espécies):
- denota a fração de fragmentos ocupados por herbívoros da espécie ( guanaco, ovelha);
- fração ocupada por predadores;
- Tempo avança discretamente e os seguintes passos ocorrem de forma síncrona:
- Colonização: um fragmento disponível pode ser colonizado pela espécie por um fragmento como primeiro vizinho ocupado, com probabilidade de colonização
- Extinção: Um fragmento ocupado pode se tornar vago pela espécie por probabilidade de extinção local
- Predação: Um fragmento que é ocupado tanto por presa quanto um predador, tem uma probabilidade de extinção da presa, dada por uma probabilidade (). Neste caso então é utilizado a probabilidade de extinção local (), ou seja, consideramos como eventos mutuamente exclusivos.
- Deslocamento competitivo: Um fragmento ocupado por ambos herbívoros, pode ser liberado do herbívoro inferior () com probabilidade .
Se temos vizinhos ocupados na vizinhança de um fragmento disponível para a colonização, a probabilidade de ser colonizado por qualquer um dos vizinhos é dado por:
- Definir os parâmetros do modelo;
- Destruir a fração de fragmentos;
- Distribuir a população inicial:
- Cada herbívoro ocupa 50% dos fragmentos disponíveis.
- O predador ocupa 50% dos fragmentos ocupados por herbívoros.
- O sistema evolui de forma síncrona seguindo regras estocástica e os eventos discutidos anteriormente;
- O sistema evolui durante um transiente (por volta de 3000 passos) até que a flutuação nas populações se estabilize;
- Média temporal: é realizada então a média temporal (tipicamente ao longo dos últimos 2000 passos da atual simulação) da fração de fragmentos ocupados por cada espécie na atua simulação.
- Média do ensemble: São realizadas nova simulações (tipicamente 100) com os mesmos parâmetros, e então é calculado médias do conjunto das frações ocupadas por cada espécie.
Um ensemble nada mais é que uma idealização consistindo de um largo número de cópias mentais de um sistema, onde cada uma destas cópias corresponde a um possível estado que o sistema pode estar. Basicamente uma coleção onde todas cópias possuem as mesmas propriedades, porém em estados diferentes[1]. Dessa forma, enquanto uma média temporal (ou espacial) é a quantidade média de uma certa quantidade de um único sistema em um certo intervalo de tempo (ou espaço), a média do ensemble é quantidade média de uma certa quantidade entre muitos sistemas idênticas em um certo momento no tempo (ou espaço)[2].
Controle de predação
Foi analisado o sistema em diferentes cenários buscando entender a dependência do estado do sistema para diferentes probabilidades de extinção de predadores e destruição do habitat. Estes parâmetros foram escolhidos pois tem origem antropogênicas. A primeira análise analisamos a a controle de predação, varia-se a probabilidade de extinção do predador () para obter a fração ocupada pelas três espécies após o sistema estar em equilíbrio. Os parâmetros são:
Além disso, para cada valor de a simulação tem a duração de 5000 passos e é calculada então a média temporal de simulação para os últimos 2000 passos. É executado 100 simulações para cada valor de e então é obtido a média do ensemble.
Destruição do habitat
A segunda análise é inspirada nos três cenários discutido no contexto. cada cenário é identificado por um fração diferente de destruição do habitat:
- Baixo conflito:
- Médio conflito:
- Alto conflito:
Para baixo e alto conflito é executado uma simulação de 9000 passos enquanto para médio conflito é executado de 18000 passos. Porém todas compartilham do fator em comum que as ovelhas são retiradas no passo e então é realizado a seguinte alteração de parâmetros para reiniciar a simulação:
Vale destacar que aqui as simulações são executadas para um valor fixo de , e que com o reinicio da simulação, as espécies apesar de manterem a mesma fração ocupada, acabam sendo redistribuídas aleatoriamente pelo habitat.
Resultados
Primeiro vamos comparando resultado da simulação do código disponível abaixo com os dados originais:
O módulo da diferença entre a fração final ocupada por cada espécie do código em Python e os dados originais foram:
Variando então a taxa de extinção local dos pumas () para e calculando as médias dos ensembles temos:
Porém devido à limitação de recursos computacionais, foi executado apenas 1 vez a simulação com cada valor . Além disso foi reproduzido o cenário para .
Conforme discutido, também foi simulado o cenário de conflitos:
| Espécie | Baixo conflito | Médio Conflito | Alto Conflito | |||
| Artigo | Meu | Artigo | Meu | Artigo | Meu | |
| Guanaco () | ||||||
| Ovelha () | ||||||
| Puma () |
Códigos
O seguinte código em fortran foi utilizado para gerar os números pseudo-aleatórios:
! Gerador de números pseudo-aleatórios ! Jhordan Silveira de Borba ! sbjhordan@gmail.com program mytest1 real RAN2 EXTERNAL RAN2 IDUM= -135 open (unit=1,file="psd.dat") DO i=1,2000000000 write(1,*),real(RAN2(IDUM)) !print *,i END DO close(1) end FUNCTION RAN2(IDUM) PARAMETER (M=714025,IA=1366,IC=150889,RM=1.4005112E-6) DIMENSION IR(97) save IR, IY DATA IFF /0/ IF(IDUM.LT.0.OR.IFF.EQ.0)THEN IFF=1 IDUM=MOD(IC-IDUM,M) DO J=1,97 IDUM=MOD(IA*IDUM+IC,M) IR(J)=IDUM END DO IDUM=MOD(IA*IDUM+IC,M) IY=IDUM ENDIF J=1+(97*IY)/M IF(J.GT.97.OR.J.LT.1)PAUSE IY=IR(J) RAN2=IY*RM IDUM=MOD(IA*IDUM+IC,M) IR(J)=IDUM RETURN END
E o seguinte código base em Python é responsável pela simulação:
# -*- coding: UTF-8 -*-
# Modelo espacialmente explícito
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
#Bibliotecas
import numpy as np # Biblioteca de funções matemáticas
import copy # Biblioteca com funções para copiar
#CONDIÇÕES INICIAIS ------------------------------------------------------
maxt = 15000 #tiempo total de cada realizacion
Lx = 100 #tamaño del sustrato
Ly = 100
#Fracciones iniciales
D = 0.3 #fraccion inicial de sitios destruidos
x10 = 0.5 #fraccion inicial de sitios ocupados por x1
x20 = 0.5 #fraccion inicial de sitios ocupados por x2
y0 = 0.5 #fraccion inicial de sitios ocupados por y
#Tasas
cx1 = 0.05 #colonizaciones
cx2 = 0.1
cy = 0.015
ex1 = 0.05 #extinciones
ex2 = 0.01
ey = 0.017
mx1y = 0.2 #depredaciones
mx2y = 0.8
depx1 = ex1+mx1y #mortalidad aumentada=extincion+depredacion
depx2 = ex2+mx2y
g = open("psd.dat", "r")
#Inicializaciones
s = np.full((Lx, Ly), [1]) #matriz de habitat (1=sitio disponible, 0=destruido)
x1 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
x2 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
y = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
for i in range(1,Lx-1):
for j in range (1,Ly-1):
rnd=float(g.readline())#np.random.rand()
if (rnd < D): s[i,j]=0
rnd=float(g.readline())#np.random.rand()
if (rnd < x10 and s[i,j]==1): x1[i,j]=1
rnd=float(g.readline())#np.random.rand()
if (rnd < x20 and s[i,j]==1): x2[i,j]=1
rnd=float(g.readline())#np.random.rand()
if ((x1[i,j]==1 or x2[i,j]==1) and rnd < y0): y[i,j]=1
for i in range(Lx): #destruimos los bordes del habitat
s[i,0]=0
s[i,Ly-1]=0
for j in range(Ly):
s[0,j]=0
s[Lx-1,j]=0
#-------------------------------------------------------
#Lazo temporal
fx1=sum(sum(x1))/((Lx-2)*(Ly-2))
fx2=sum(sum(x2))/((Lx-2)*(Ly-2))
fy =sum(sum(y)) /((Lx-2)*(Ly-2))
f = open("minha.dat", "w")
f.write(" "+str(0)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n")
for it in range(maxt):
if (float(it)%(float(maxt)/100)==0.):
print("Porcentagem: "+str(it*100/maxt)) # Exibe o passo atual
x1old=copy.copy(x1) #poblaciones del paso anterior
x2old=copy.copy(x2)
yold=copy.copy(y)
#Recorro la malla
for i in range (1,Lx-1):
for j in range (1,Ly-1):
#colonizaciones
if (x1old[i,j]==0 and s[i,j]==1): #colonizacion de x1 si el sitio esta libre de x1 y no destruido:
nvec=x1old[i-1,j]+x1old[i+1,j]+x1old[i,j-1]++x1old[i,j+1] #cantidad de vecinos ocupados
p=1.0-(1.0-cx1)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre
rnd=float(g.readline())#np.random.rand()
if (rnd < p):x1[i,j]=1
if (x2old[i,j]==0 and s[i,j]==1 and x1old[i,j]==0): #colonizacion de x2 si el sitio esta libre de x1 y x2, y no destruido:
nvec=x2old[i-1,j]+x2old[i+1,j]+x2old[i,j-1]+x2old[i,j+1] #cantidad de vecinos ocupados
p=1.0-(1.0-cx2)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre
rnd=float(g.readline())#np.random.rand()
if (rnd < p): x2[i,j]=1
ocup=0 #ocupacion de herbivoros
if (x1old[i,j]==1 or x2old[i,j]==1): ocup=1
if (yold[i,j]==0 and ocup==1): #colonizacion de y si el sitio está libre de y,y ocupado por un x
nvec=yold[i-1,j]+yold[i+1,j]+yold[i,j-1]+yold[i,j+1] #cantidad de vecinos ocupados
p=1.0-(1.0-cy)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre
rnd=float(g.readline())#np.random.rand()
if (rnd < p): y[i,j]=1
#extinciones sin depredadores
if (x1old[i,j]==1 and yold[i,j]==0): #extincion de x1 si el sitio esta ocupado
rnd=float(g.readline())#np.random.rand()
if (rnd < ex1): x1[i,j]=0
if (x2old[i,j]==1 and yold[i,j]==0): #extincion de x2 si el sitio esta ocupado
rnd=float(g.readline())#np.random.rand()
if (rnd < ex2): x2[i,j]=0
if (yold[i,j]==1): #extincion de y si el sitio esta ocupado
rnd=float(g.readline())#np.random.rand()
if (rnd < ey): y[i,j]=0
#depredacion (extinción de presas donde hay depredadores)
if (x1old[i,j]==1 and yold[i,j]==1): #depredacion de y sobre x1
rnd=float(g.readline())#np.random.rand()
if (rnd < depx1): x1[i,j]=0
if (x2old[i,j]==1 and yold[i,j]==1): #depredacion de y sobre x2
rnd=float(g.readline())#np.random.rand()
if (rnd < depx2): x2[i,j]=0
#desplazamiento por competencia (jerarquia)
if (x1old[i,j]==1 and x2old[i,j]==1):
rnd=float(g.readline())#np.random.rand()
if (rnd < cx1): x2[i,j]=0
fx1=sum(sum(x1))/((Lx-2)*(Ly-2))
fx2=sum(sum(x2))/((Lx-2)*(Ly-2))
fy =sum(sum(y)) /((Lx-2)*(Ly-2))
f.write(" "+str(it+1)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n")
f.close
g.close()
Além disso, foi usado o script em R para gerar os gráficos comparando dois conjunto de dados, este script é facilmente editável pra exibir o resultado de apenas uma simulação:
# Visualização de gráficos
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
Dados0 <- read.table("Endereço do arquivo 0")
Dados1 <- read.table("Endereço do arquivo 1")
par(mfrow=c(1,2))
plot( c(Dados0[,1]), c(Dados0[,2]), col="black", main="Original", ylab="Fração", xlab="passo" ,type="l",ylim=c(0,0.5))
lines(c(Dados0[,1]), c(Dados0[,3]), col="blue")
lines(c(Dados0[,1]), c(Dados0[,4]), col="red")
legend("topright", c("Guanacos","Ovelhas","Pumas"), fill=c("black","blue","red"))
plot( c(Dados1[,1]), c(Dados1[,2]), col="black", main="Meu", ylab="Fração", xlab="passo" ,type="l",ylim=c(0,0.5))
lines(c(Dados1[,1]), c(Dados1[,3]), col="blue")
lines(c(Dados1[,1]), c(Dados1[,4]), col="red")
legend("topright", c("Guanacos","Ovelhas","Pumas"), fill=c("black","blue","red"))
Principal material utilizado
- Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances (Fabiana Laguna e outros, Ecological Modelling)
Referências
- ↑ Statistical Ensembles (Instituto de Tecnologia de Massachusetts)
- ↑ Mathematical Methods (Yoshihisa Yamamoto, Instituto Nacional de Informática)
Anterior: Modelo de Levins aprimorado para 3 espécies | Índice: Ecologia | Próximo: -