Modelo de Levins aprimorado para 3 espécies: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 3: | Linha 3: | ||
Para três espécies o modelo de Levins se torna: | Para três espécies o modelo de Levins se torna: | ||
<math>\begin{align} | <math display="block">\begin{align} | ||
\frac{dx_{1}}{dt}= & c_{1}x_{1}\left(1-D-x_{1}\right)-e_{1}x_{1}-\mu_{1}x_{1}y \\ | \frac{dx_{1}}{dt}= & c_{1}x_{1}\left(1-D-x_{1}\right)-e_{1}x_{1}-\mu_{1}x_{1}y \\ | ||
\frac{dx_{2}}{dt}= & x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu_{2}y+c_{x_{1}}x_{1}\right)\right] \\ | \frac{dx_{2}}{dt}= & x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu_{2}y+c_{x_{1}}x_{1}\right)\right] \\ | ||
| Linha 21: | Linha 21: | ||
====== Ovelha ====== | ====== Ovelha ====== | ||
<math>\frac{dx_{2}}{dt}= x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu_{2}y+c_{x_{1}}x_{1}\right)\right]</math> | <math display="block">\frac{dx_{2}}{dt}= x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu_{2}y+c_{x_{1}}x_{1}\right)\right]</math> | ||
A ovelha talvez tenha a dinâmica mais complexa do sistema, pois é tanto um competidor inferior ao gunaco, quanto uma presa para o puma, e isso interfere diretamente nos fragmentos disponíveis para a colonização. Pensando em probabilidade e conectando a probabilidade de ocorrer a colonização, é dada pela probabilidade de que cada tentativa de colonização tenha sucesso <math display="inline">c_{2}</math> '''e''' a probabilidade de selecionarmos um fragmento disponível pra as ovelhas é <math display="inline">P\left(F_{D}^{O}\right)</math>. Lembrando que para o caso do guanaco, isso era apenas:<math display="block">P\left(F_{D}^{G}\right)=\left(1-D-x_{1}\right)</math>Pois probabilidade de selecionarmos um fragmento destruído é <math display="inline">D</math>, e de selecionarmos um fragmento ocupado por guanacos é <math display="inline">x_{1}</math>, e são eventos independentes, isto é, nunca temos um fragmento destruído com guanacos. Então a probabilidade de selecionarmos um fragmento que o guanaco não pode colonizar é dado por <math display="inline">D+x_{1}</math>, uma vez que são eventos mutuamente exclusivos. Por complementaridade a probabilidade de selecionarmos um fragmento que o guanaco pode colonizar é dado por <math display="inline">1-\left(D+x_{1}\right)</math>. | A ovelha talvez tenha a dinâmica mais complexa do sistema, pois é tanto um competidor inferior ao gunaco, quanto uma presa para o puma, e isso interfere diretamente nos fragmentos disponíveis para a colonização. Pensando em probabilidade e conectando a probabilidade de ocorrer a colonização, é dada pela probabilidade de que cada tentativa de colonização tenha sucesso <math display="inline">c_{2}</math> '''e''' a probabilidade de selecionarmos um fragmento disponível pra as ovelhas é <math display="inline">P\left(F_{D}^{O}\right)</math>. Lembrando que para o caso do guanaco, isso era apenas:<math display="block">P\left(F_{D}^{G}\right)=\left(1-D-x_{1}\right)</math>Pois probabilidade de selecionarmos um fragmento destruído é <math display="inline">D</math>, e de selecionarmos um fragmento ocupado por guanacos é <math display="inline">x_{1}</math>, e são eventos independentes, isto é, nunca temos um fragmento destruído com guanacos. Então a probabilidade de selecionarmos um fragmento que o guanaco não pode colonizar é dado por <math display="inline">D+x_{1}</math>, uma vez que são eventos mutuamente exclusivos. Por complementaridade a probabilidade de selecionarmos um fragmento que o guanaco pode colonizar é dado por <math display="inline">1-\left(D+x_{1}\right)</math>. | ||
| Linha 33: | Linha 33: | ||
====== '''Puma''' ====== | ====== '''Puma''' ====== | ||
<math>\frac{dy}{dt}= y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right] </math> | <math display="block">\frac{dy}{dt}= y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right] </math> | ||
Começando com a parte simples do que já discutimos, a população é reduzida devido a um fator de extinção <math display="inline">e_{y}</math>, e não temos predação, pois o puma é próprio predador. <div class="center">[[Ficheiro:Veinn.png|esquerda|miniaturadaimagem|208x208px|[https://pt.wikipedia.org/wiki/Diagrama_de_Venn Diagrama de Veinn] representando os conjuntos envolvidos no sistema.]] | Começando com a parte simples do que já discutimos, a população é reduzida devido a um fator de extinção <math display="inline">e_{y}</math>, e não temos predação, pois o puma é próprio predador. <div class="center">[[Ficheiro:Veinn.png|esquerda|miniaturadaimagem|208x208px|[https://pt.wikipedia.org/wiki/Diagrama_de_Venn Diagrama de Veinn] representando os conjuntos envolvidos no sistema.]] | ||
Edição das 20h48min de 13 de abril de 2021
Anterior: Modelo de Levins aprimorado para 2 espécies | Índice: Ecologia | Próximo: Modelo espacialmente explícito
Para três espécies o modelo de Levins se torna:
Guanaco
O termo responsável pelo aumento na população é o que representa a colonização. Podemos pensar em termos probabilísticos, que temos 3 eventos independentes:
- Probabilidade de selecionar um fragmento com um guanaco disponível para tentar a colonização;
- Probabilidade selecionar um fragmento disponível para ser colonizado;
- Probabilidade de que cada tentativa de colonização tenha sucesso.
A queda na população acontece por dois termos que representam dois eventos diferentes:
- Extinção local: depende da taxa . Temos como dois eventos independentes a probabilidade selecionar um fragmento com guanaco e a probabilidade de que cada guanaco sofra a extinção local.
- Predação: depende da população de predadores e a taxa de predação . Novamente podemos interpretar como três eventos independentes. Probabilidade de selecionarmos uma puma, probabilidade de selecionarmos um guanaco e probabilidade de ocorrer a predação a cada encontro. Assim como o modelo de Lotka-Volterra, a predação é proporcional a população de ambas as espécies.
Ovelha
A ovelha talvez tenha a dinâmica mais complexa do sistema, pois é tanto um competidor inferior ao gunaco, quanto uma presa para o puma, e isso interfere diretamente nos fragmentos disponíveis para a colonização. Pensando em probabilidade e conectando a probabilidade de ocorrer a colonização, é dada pela probabilidade de que cada tentativa de colonização tenha sucesso e a probabilidade de selecionarmos um fragmento disponível pra as ovelhas é . Lembrando que para o caso do guanaco, isso era apenas:
Agora precisamos considerar os fragmentos que estão destruídos e os ocupados por ovelhas ou guanacos. Mas a ocupação de guanacos e ovelhas não é exclusiva, isto é, temos fragmentos ocupados por guanacos e ovelhas. Então a probabilidade de selecionarmos um fragmento ocupado por guanaco ou ovelha é dado por , uma vez são eventos independentes. Sendo assim a probabilidade de selecionarmos um fragmento indisponível é dado por . E novamente recorrendo a complementaridade, a probabilidade de selecionarmos um fragmento disponível para a ovelha é dada por então por .
De resto, a população diminui de forma semelhante ao guanaco:
- Termo de extinção local: proporcional a taxa de extinção local ;
- Termo de predação: proporcional a população de predadores e a taxa de predação .;
- Termo de deslocamento: ocorre devido a competição hierárquica e matematicamente é idêntico a predação, apenas substituímos e .
Puma
Começando com a parte simples do que já discutimos, a população é reduzida devido a um fator de extinção , e não temos predação, pois o puma é próprio predador.
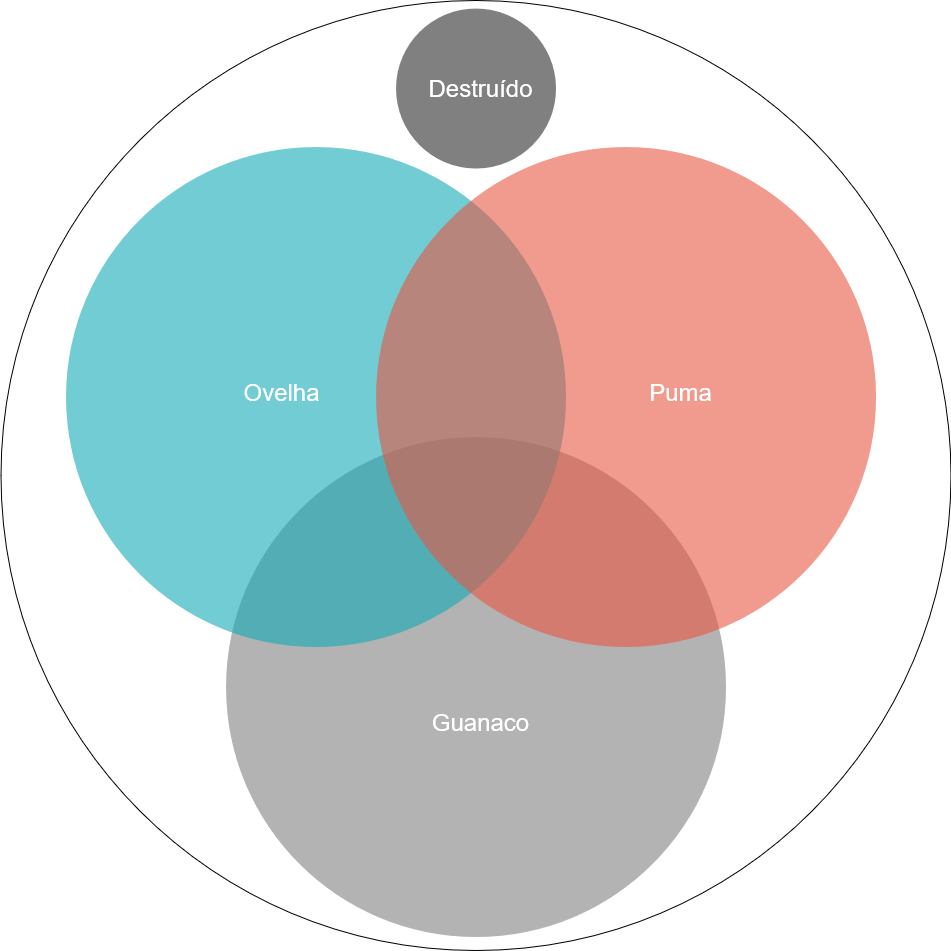
Agora novamente a parte complexa reside na hora de levarmos em conta a probabilidade de selecionarmos um fragmento disponível. Precisamos considerar todos os fragmentos ocupados ocupados por guanacos ou ovelhas. E quando fazemos isso, precisamos tomar cuidado para não contar duas vezes fragmentos que estejam ocupados por ambas as espécies, então temos . Além disso, também precisamos descontar os fragmentos que já estão ocupados por pumas, então precisamos descontar os que possuem guanaco e puma , ovelha e puma . Porém novamente, não podemos descontar duas vezes os fragmentos que possuem ovelha, guanaco e puma, então é necessário "devolver" . Temos então:
Como são todos eventos independentes:
Principal material utilizado
- Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances (Fabiana Laguna e outros, Ecological Modelling)
Anterior: Modelo de Levins aprimorado para 2 espécies | Índice: Ecologia | Próximo: Modelo espacialmente explícito
![{\displaystyle {\begin{aligned}{\frac {dx_{1}}{dt}}=&c_{1}x_{1}\left(1-D-x_{1}\right)-e_{1}x_{1}-\mu _{1}x_{1}y\\{\frac {dx_{2}}{dt}}=&x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu _{2}y+c_{x_{1}}x_{1}\right)\right]\\{\frac {dy}{dt}}=&y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4444c86924b1c8ccbe06e3a0d4daa0810fb7188c)
![{\displaystyle {\frac {dx_{1}}{dt}}=x_{1}\left[c_{1}\left(1-D-x_{1}\right)-\left(e_{1}+\mu _{1}y\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45780c155e0b7dc74b67c355560f93a09a3671fa)










![{\displaystyle {\frac {dx_{2}}{dt}}=x_{2}\left[c_{2}\left(1-D-x_{1}-x_{2}+x_{1}x_{2}\right)-\left(e_{2}+\mu _{2}y+c_{x_{1}}x_{1}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8210254bd39cee171327567c3abf27ca544e4fa8)













![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[\left(x_{1}+x_{2}-x_{1}x_{2}\right)-y\left(x_{1}+x_{2}-x_{1}x_{2}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a089f756adf720cbde0c3032e1d6dfdd06dea324)





![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[P\left(x_{1}\cup x_{2}\right)-P\left(x_{1}\cap y\right)-P\left(x_{2}\cap y\right)+P\left(x_{2}\cap y\cap x_{1}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38c975e8999819e0d580c47695965f68bba00c7d)
![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[P\left(x_{1}\right)+P\left(x_{2}\right)-P\left(x_{1}\cap x_{2}\right)-P\left(x_{1}\cap y\right)-P\left(x_{2}\cap y\right)+P\left(x_{2}\cap y\cap x_{1}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47cf55fd2b4caca9fd1da33f7d3fb77f35c59165)
![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[P\left(x_{1}\right)+P\left(x_{2}\right)-P\left(x_{1}\right)P\left(x_{2}\right)-P\left(x_{1}\right)P\left(y\right)-P\left(x_{2}\right)P\left(x_{y}\right)+P\left(x_{1}\right)P\left(x_{2}\right)P\left(x_{y}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d6033cca4b3a2ee2b5f9f820f55c0cc7e26d72c)
![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[x_{1}+x_{2}-x_{1}x_{2}-x_{1}y-x_{2}y+x_{1}x_{2}y\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b75ceec5c4bc7ad9cde132a44759580d3b13a2)

![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left[P\left(x_{1}\cup x_{2}\right)-P\left(y\right)P\left(x_{1}\cup x_{2}\right)\right]-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5654970881fed4773c29673c7e349eb86928f8ad)
![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}\left(1-P\left(y\right)\right)P\left(x_{1}\cup x_{2}\right)-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17993cbe44dcac8c5e0009ac8b8fd485783da74)

![{\displaystyle {\frac {dy}{dt}}=y\left[c_{y}P\left(y\right)^{c}P\left(x_{1}\cup x_{2}\right)-e_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6210c695ef59c0ebb4895556a7efe5c5fa1fc2ff)

