Modelo de Gray-Scott
Grupo: Paula Pandolfo, Ramiro de Souza e Wallace Carvalho
Objetivo: Este trabalho tem como objetivo principal implementar numericamente o modelo de Gray-Scott bidimensional, um tipo particular de sistema de reação-difusão, a fim de ilustrar, entre outras características, a emergência da complexidade através de equações de relativa simplicidade matemática. Para isso, primeiramente, será introduzida a formalidade do modelo: suas equações diferenciais e seus estados estacionários. Analisar-se-ão, também, as condições em que tais estados são estáveis ou não, e se aqueles que forem estáveis assim permanecem após a introdução de processos difusivos. Os resultados da implementação serão comparados com aqueles obtidos por uma das referências principais, Introduction to the Modeling and Analysis of Complex Systems, por Hiroki Sayama. A comparação mostrará uma boa concordância qualitativa, apesar de ficarem também perceptíveis discrepâncias com as simulações feitas por Sayama, indicando, possivelmente, uma alta sensibilidade dos resultados com a resolução e/ou condições iniciais utilizadas.
Introdução
Sistemas de reação-difusão são modelos matemáticos de grande importância, que podem ser aplicados a múltiplas situações. Sua principal aplicação, como o nome sugere, é na descrição da cinética química; mais especificamente, em como evoluem no tempo as concentrações de múltiplas substâncias em cada ponto do espaço, dado um determinado conjunto de reações associadas a essas espécies químicas que, ademais, também podem se difundir no meio. As equações diferenciais que descrevem tal sistema são um conjunto de equações em que a variação temporal das concentrações depende de termos de reação (funções associadas às reações químicas e à reposição ou não das espécies envolvidas) e de difusão (termos proporcionais ao laplaciano ):[1]
Sistemas descritos por equações como essas oferecem uma descrição matemática relativamente simples, com separação clara entre dinâmica não espacial e espacial, sendo a última ainda mais facilitada por ser descrita apenas por um termo laplaciano, que simplifica incorporar difusão a um problema que, inicialmente, possui apenas termos de reação. Além disso, a forma das equações atalha a análise de estabilidade, obtida através da matriz Jacobiana dos termos de reação.[1]
Dentre as mais diversas possibilidades de reações químicas e reagentes envolvidos, vamos estudar um caso simples: o modelo de Gray-Scott. Este modelo foi primeiramente introduzido por Peter Gray e Steve Scott entre os anos de 1983 e 1985,[2][3][4] e foi popularizado por John Pearson nos anos 1990.[5] Como Pearson sugere já no título de seu texto ("Padrões Complexos em um Sistema Simples", em português), tal dinâmica de reação-difusão produz, a partir de um modelo matematicamente simples, um conjunto variado de padrões complexos, não dessemelhantes àqueles encontrados na evolução de células biológicas,[5][6] sendo, portanto, de profundo interesse enquanto exemplo de emergência de complexidade na natureza.
Descrição do modelo
O modelo de Gray-Scott descreve uma reação autocatalítica. Sejam duas substâncias químicas cujas concentrações em um dado ponto do espaço são dadas pelas variáveis e , a reação pode ser representada como
Isso significa que uma molécula da substância é transformada em uma molécula da substância por meio da ação de outras duas moléculas da substância , ou seja, é um catalisador de sua própria produção (daí o termo autocatálise).[6] Além dessa reação, ambas as substâncias difundem-se pelo meio (por isso este modelo pertence à classe mais geral de modelos reativos-difusivos) e, dessa forma, as concentrações e mudam com o tempo e diferem em cada ponto. Por simplicidade, assume-se que a reação reversa (i.e., ) não ocorre.
O comportamento geral do sistema pode ser descrito pelas equações diferenciais parciais abaixo:[6]
A primeira das equações acima pode ser interpretada da seguinte forma: em um dado ponto, a variação na concentração aumenta proporcionalmente ao laplaciano de naquele ponto — ou seja, quando a concentração na vizinhança desse ponto é alta —, e proporcionalmente à taxa de reposição de (taxa de alimentação, ou feed rate); a concentração diminui com o termo reativo , que representa a reação .
Já na segunda equação, a concentração aumenta com o termo reativo e também proporcionalmente ao laplaciano de naquele ponto, mas diminui com a remoção de a uma taxa , mais rápida, portanto, do que a reposição de .
Assim, tem-se que e são os parâmetros do modelo, juntamente com os coeficientes de difusão e .
Uma maneira de compreender esse sistema é imaginá-lo como consistindo de duas substâncias e , envoltas por uma membrana semipermeável e imersas em um meio em que essas mesmas duas substâncias estão presentes. A membrana permite a entrada da substância , mas não da substância , e permite a saída da substância , mas não da substância .[7]
Análise de estabilidade linear
Nota: A análise em toda esta seção pressupõe sempre que os parâmetros e coeficientes de difusão são positivos.
Soluções estacionárias sem difusão
O modelo de Gray-Scott depende dos parâmetros e dos coeficientes de difusão das espécies químicas. Ignorando em um primeiro momento os termos de difusão, percebe-se que, por inspeção, o sistema possui uma solução estacionária em para quaisquer valores dos parâmetros. Esse ponto, no entanto, não é a única solução estacionária do sistema; para encontrar as outras, é necessário impor nas equações do sistema. Fazendo isso e dispensando os termos de difusão (), obtém-se o seguinte sistema de equações:
Somando essas duas equações, relacionamos as variáveis e :
onde definiu-se o parâmetro auxiliar .
Substituindo na segunda equação do sistema (2) (e reescrevendo ), ficamos com:
Evidentemente, é solução dessa equação, implicando em , como já havíamos inspecionado. Alternativamente, considerando , podemos dividir (4) por , ficando com . Resolvendo esta equação quadrática, obtemos duas novas soluções estacionárias para :
Disso, pela relação (3), temos que os valores correspondentes para são:
É necessário apontar que, para que as duas últimas soluções (não-triviais) existam — isto é, sejam números reais — o fator dentro da raiz quadrada tem de ser positivo ( ). Por consequência:
- , para que existam as soluções não-triviais.
Nesse caso, então, há três soluções estacionárias do sistema:[8]
Estabilidade dos estados estacionários (sem difusão)
Para avaliar a estabilidade das soluções acima, faz-se necessário obter a matriz Jacobiana dos termos de reação, . Explicitamente, analisando o sistema (1) de equações, temos que e . A matriz Jacobiana do sistema é então dada por:
Analisemos a estabilidade para os três pares de soluções estacionárias:
- Para :
- Por essa ser uma matriz diagonal, os autovalores são justamente as entradas das diagonais; ou seja, e . Uma vez que e são parâmetros positivos, os dois autovalores são reais e negativos, e portanto o ponto é sempre estável.
- Para , podemos utilizar uma estratégia que simplifica as contas. Em particular, nota-se que os dois pontos obedecem à segunda equação do sistema (2) com . Desse modo, se dividirmos tal equação por , percebemos que ambos os pontos obedecem a:
- Dessa equação, podemos calcular as entradas da segunda coluna da matriz jacobiana com facilidade:
- Assim, a matriz jacobiana desses pontos fica:
- Sabemos que o produto dos autovalores dessa matriz é igual ao seu determinante. Calculando-o, obtém-se:
- Dividindo por :[8]
- onde se definiu (observação: este é o definido no Gros[8]). Nota-se que a condição de existência para os dois pontos não-triviais é equivalente a . Expandindo os termos, é possível mostrar que a expressão acima pode ser reescrita como:
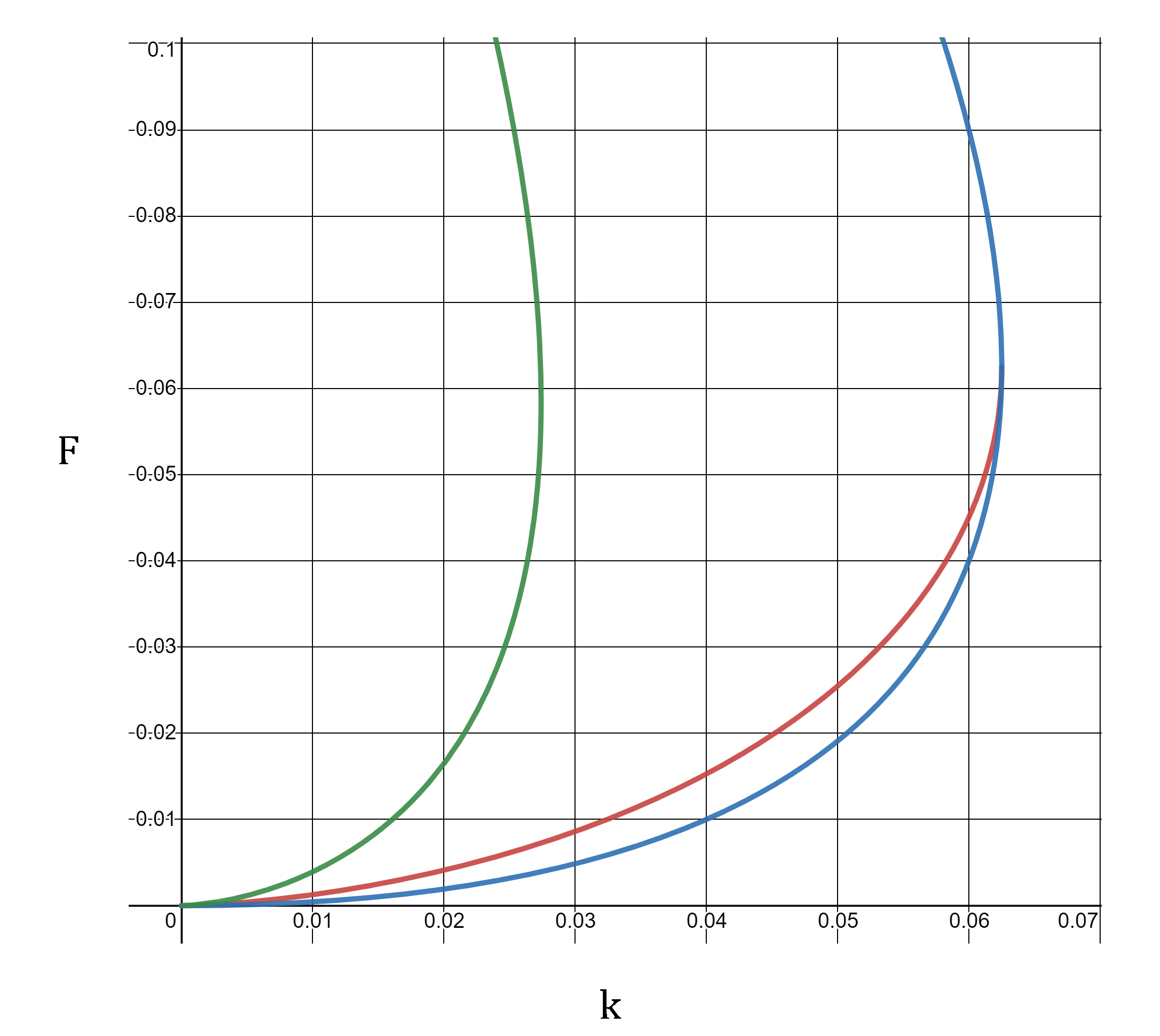
- Para o caso (sinal negativo em (11)), temos a cota superior . Portanto, para todo que satisfaça a condição de existência. Como o determinante é negativo, sabemos que os autovalores são reais (comentário: como as entradas da matriz são reais, se os autovalores fossem complexos, seriam também conjugados, de modo que o produto deles fosse igual ao módulo ao quadrado de qualquer um, que seria um valor positivo). Ademais, como seu produto é negativo, eles têm sinais opostos; isto é, um deles é positivo, de modo que o ponto nunca seja estável. Assim, esse ponto sempre será um ponto de sela.[8] Depreendemos desse raciocínio que o determinante da matriz jacobiana de entradas reais ser positivo é uma condição necessária para que haja estabilidade do ponto.
- Já para (sinal positivo em (11)), temos sempre que . Para verificar a estabilidade, temos que agora calcular o traço da matriz jacobiana, pois o traço é a soma dos autovalores: se os autovalores são reais, eles têm o mesmo sinal por seu determinante ser positivo, de modo que o traço compartilhe o sinal com os dois autovalores; se os autovalores são complexos, eles serão conjugados e o traço será , de modo que a parte real dos autovalores tenha o mesmo sinal do traço. Assim, basta que o traço seja negativo para que o ponto seja estável, e que seja positivo para que seja instável. No caso, temos que:
- Esse traço é negativo quando e positivo quando ; ou seja, é estável quando e instável quando (lembrando que para todo e ). Desse modo, pode-se caracterizar uma transição de estabilidade quando .
- Utilizando simultaneamente as equações (3) e (8), obtemos:[8]
- Substituindo , obteremos ao final:[8]
- Que é uma relação entre e que caracteriza a fronteira de estabilidade para o ponto .
- Como um fato adicional, podemos separar quando é um nó estável (stable node) de quando ele é um foco estável (stable focus). Um nó estável ocorre quando os autovalores da matriz jacobiana forem reais, enquanto o foco ocorrem quando forem complexo-conjugados. Sabendo que os autovalores podem ser escritos como[10]
- Vemos que a fronteira entre nó e foco para o ponto é caracterizada por . O resultado de todas essas fronteiras é o diagrama de fases da Figura 1, baseado no gráfico feito por Gros.[9]
Estabilidade dos estados estacionários (com difusão)
Precisamos agora analisar a estabilidade dos pontos estacionários na presença de difusão, como prescreve o sistema de equações (1), que descreve o modelo. Para isso, é necessário levar em consideração, para cada um dos estados de equilíbrio, os autovalores da matriz , em que é a matriz diagonal cujas entradas são e :[11]
Se escrevermos, genericamente, que , teremos a seguinte matriz jacobiana de reação-difusão:
Como já detalhado acima, para que o ponto seja estável, tal matriz tem que ter a parte real de todos os seus autovalores negativa, de modo que seu determinante seja positivo () e seu traço negativo ().[12] Impondo tais condições à matriz acima, obteremos, após manipulações:[11]
Se o traço é negativo, vemos que a segunda equação é imediatamente satisfeita, pois o lado esquerdo é positivo em qualquer situação.[11] Para este trabalho, interessa-nos apenas verificar se o estado estacionário permanece estável após a introdução da difusão. Dispensaremos a análise do ponto , pois nossas simulações não o incluirão como ponto estável, nem mesmo desconsiderando difusão.
Para o ponto , utilizamos a matriz (7), obtendo as seguintes desigualdades:
Que são, evidentemente, satisfeitas, por análise simples de sinais de cada lado. Portanto, conclui-se que o ponto é sempre estável, inclusive na presença de difusão.
Esse é um resultado, à primeira vista, surpreendente. Em geral, o surgimento de padrões complexos e não homogêneos em sistemas reativos-difusivos está relacionado à desestabilização de um ou mais estados de equilíbrio homogêneo causada pela introdução dos coeficientes de difusão (conhecida como instabilidade de Turing).[13] Entretanto, no caso do modelo de Gray-Scott, o surgimento de padrões complexos e não homogêneos não decorre da instabilidade de Turing, uma vez que o surgimento de padrões não-triviais neste modelo ocorre mesmo quando apenas o estado de equilíbrio trivial existir,[14] como veremos nas simulações da seção de resultados.
Implementação numérica
O método usado para integrar as equações diferenciais parciais do modelo foi o FTCS (Foward Time Central Space). Como existem explicações do método em toda literatura e em outras entradas da Wiki (ver, por exemplo, Modelo de Turing), a explicação aqui será sucinta.
O método consiste em discretizar a derivada parcial em relação ao tempo para frente e discretizar as derivadas parciais de segunda ordem em relação ao espaço centralmente (isto é, levando em consideração os pontos adjacentes ao ponto em que ela é calculada). Para uma função :
Das duas últimas equações acima, é fácil mostrar que o laplaciano em duas dimensões, presente nas equações do sistema (1) deste trabalho, pode ser escrito como
Utilizando passos de mesmo tamanho nas direções e , ou seja, fazendo , pode-se simplificar a discretização do laplaciano para
Usando a notação e definindo as separações de pontos como , , , fica possível então escrever as equações do modelo de forma discretizada:
Utilizou-se uma rede quadrada de tamanho . O estado inicial do sistema é aquele em que todos os pontos estão no estado de equilíbrio estável trivial , exceto o ponto central, em que é introduzida uma perturbação com .
Foram usadas condições de fronteira totalmente periódicas. Cada elemento na matriz tem quatro vizinhos, denominados U (Up), D (Down), L (Left), R (Right). Na Figura 2, o elemento , possui os vizinhos , , , ; o elemento possui como vizinhos , , , ; o elemento tem vizinhos , , , ; e, finalmente, os vizinhos de são , , e .
Resultados e discussão
As simulações abaixo reproduzem algumas condições simuladas por Sayama.[15]
| Simulações do Modelo de Gray-Scott para a concentração , com . A concentração é maior nas áreas mais claras. | |
|---|---|
| Simulações do Modelo de Gray-Scott para a concentração , com . Nos dois casos abaixo, a concentração é menor nas áreas mais claras. | |
|---|---|
Em geral, todas as simulações apresentaram boa concordância qualitativa com os padrões simulados por Sayama;[15] entretanto, as imagens não são isomorficamente equivalentes. Seguem abaixo mais exemplos de simulações:
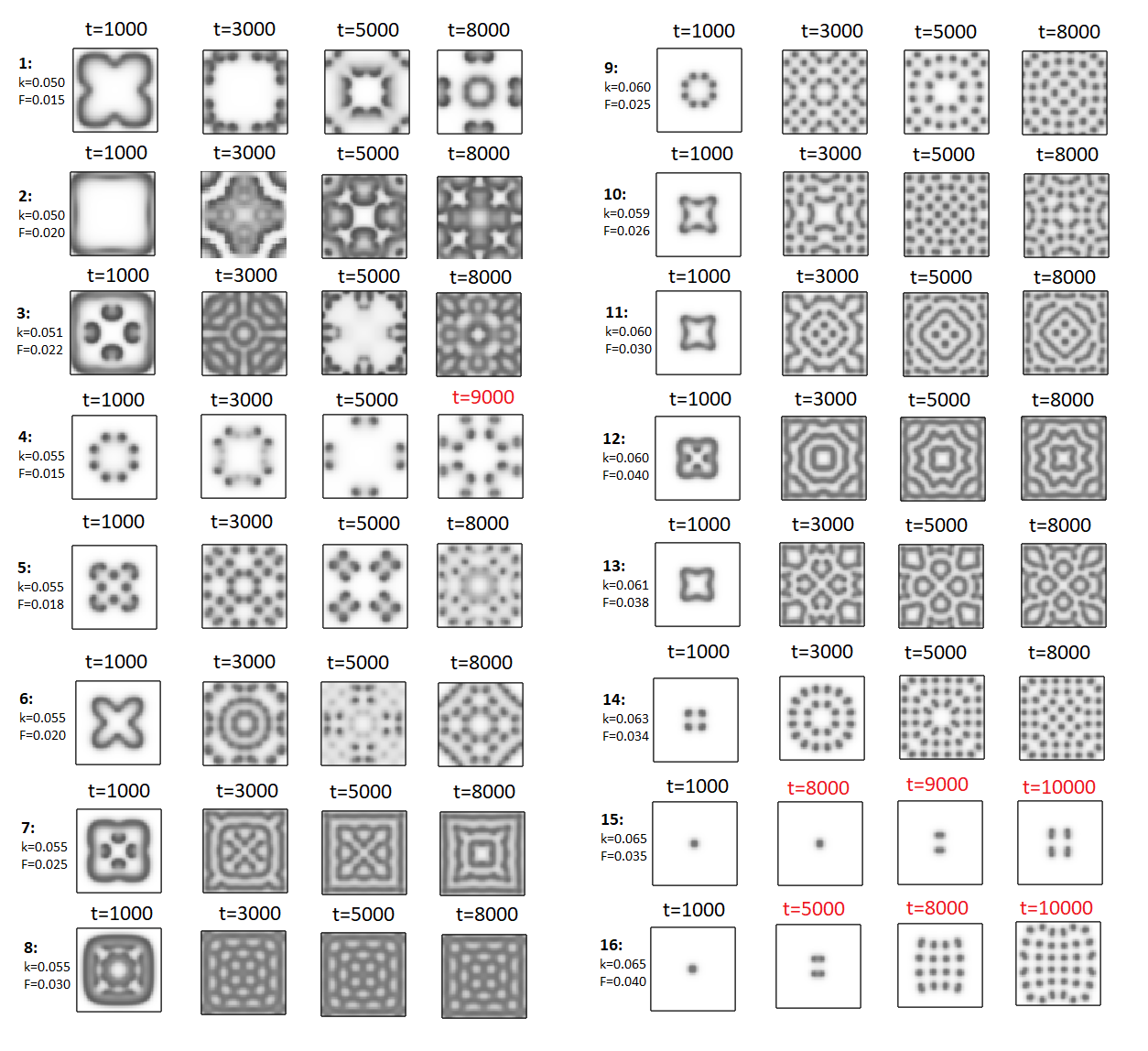
Uma explicação possível para as discrepâncias observadas é o tamanho do grid utilizado e a aplicação das condições iniciais. Possivelmente, Sayama usou um grid de tamanho par, como , por exemplo, e escolheu dois ou quatro pontos no centro da matriz como condição inicial. Como se trata da simulação de um sistema não linear, os resultados são muito sensíveis às condições iniciais. Além disso, observamos uma forte dependência de alguns padrões formados em relação à resolução espacial, , e em relação à resolução temporal, (os valores que utilizamos no programa mostraram a melhor concordância com o comportamento qualitativo conhecido nos pontos testados).
Segue abaixo uma amostragem de algumas simulações realizadas e suas posições no diagrama de fases do modelo:
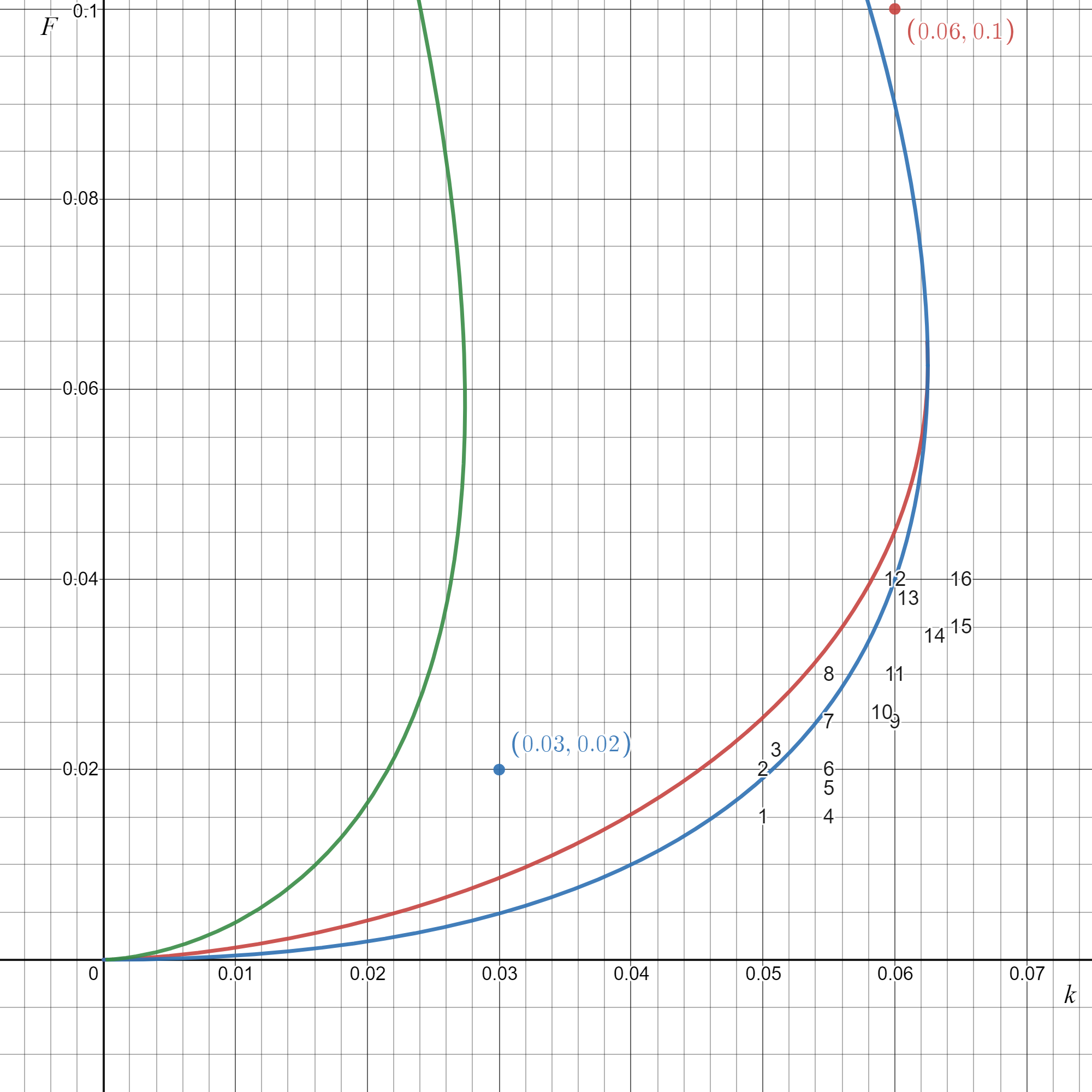
Na Figura 4 é possível observar que a grande maioria das condições que geram padrões complexos está na vizinhança da curva , próximo à saliência, no intervalo e .
Nota-se que, de fato, muitos padrões são gerados com a condição (à direita da curva azul), ou seja, na região onde o único estado de equilíbrio é o estado trivial . Como esse estado é sempre estável (ver [2]), independentemente dos valores dos coeficientes de difusão, a instabilidade de Turing não explica a formação de padrões nesses casos.
Ainda em relação à Figura 4, o ponto em vermelho (classificado como "R" por Pearson[5]), com , é um exemplo em que a taxa de alimentação de é muito grande em relação à taxa de eliminação () de , de modo que o sistema rapidamente atinge o equilíbrio trivial em todos os pontos. De outro lado, o ponto em azul (classificado como "B" por Pearson[5]), com , é um exemplo contrário, em que a taxa de eliminação () de é muito grande em relação à taxa de alimentação de , de modo que, para tempos longos, também não há formação de padrões, mas o estado que se atinge é tal que a concentração de é próxima de .
O modelo de Gray-Scott é reconhecido por exibir grande riqueza de padrões. Esses padrões foram originalmente classificados por Pearson.[5] Uma classificação aprimorada, mais recente, pode ser encontrada nas referências.[16] A classificação, de acordo com letras do alfabeto grego (, , , etc), leva em consideração a dinâmica e a formação de padrões complexos estáveis ou não para tempos longos, em que os sistemas, para dadas condições, atingem uma espécie de equilíbrio. Alguns dos padrões formados são linhas (stripes), manchas, pontos, padrões hexagonais. Essas formas estão em constante transformação por um período, interagindo umas com as outras, dividindo-se, mesclando-se. Eventualmente, dependendo das condições, alguns sistemas atingem um padrão estável; outros nunca se estabilizam. Alguns são mais lentos, outros mais rápidos. Por exemplo, padrões do tipo levam muito tempo para se formar (não conseguimos observar padrões desse tipo). Outros sistemas dependem muito mais do que outros do tamanho do grid e das condições iniciais (por exemplo, sistemas do tipo , que também não conseguimos observar).
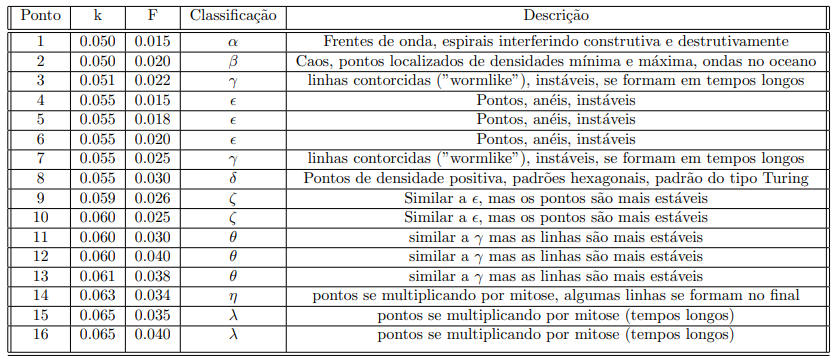
A Tabela 1 é uma tentativa de classificar os resultados observados nas simulações de acordo com a padronização normalmente adotada. A descrição é informal e relata parcialmente o que foi observado. Obviamente pode conter erros, mas demonstra, no geral, que a simulação conseguiu reproduzir o comportamento qualitativo esperado dos pontos mostrados no espaço de fases da Figura 4, o que é um resultado notável para um método tão simples como o FCTS, com um grid pequeno e tempo/recurso computacional limitados.
Programa
Referências
- ↑ 1,0 1,1 Sayama, p. 259
- ↑ P. Gray and S. Scott, “Autocatalytic reactions in the isothermal, continuous stirred tank reactor: isolas and other forms of multistability,” Chemical Engineering Science, vol. 38, no. 1, pp. 29–43, 1983.
- ↑ P. Gray and S. Scott, “Autocatalytic reactions in the isothermal, continuous stirred tank reactor: Oscillations and instabilities in the system A+2B → 3B; B → C,” Chemical Engineering Science, vol. 39, no. 6, pp. 1087–1097, 1984.
- ↑ P. Gray and S. Scott, “Sustained oscillations and other exotic patterns of behavior in isothermal reactions,” Journal of Physical Chemistry, vol. 89, no. 1, pp. 22–32, 1985.
- ↑ 5,0 5,1 5,2 5,3 5,4 J. E. Pearson, “Complex patterns in a simple system,” Science, vol. 261, no. 5118, pp. 189–192, 1993. PDF
- ↑ 6,0 6,1 6,2 Sayama, p. 266
- ↑ Reaction-Diffusion by the Gray-Scott Model: Pearson's Parametrization
- ↑ 8,0 8,1 8,2 8,3 8,4 8,5 Gros, p. 113
- ↑ 9,0 9,1 Gros, p. 114
- ↑ Sayama, p. 123
- ↑ 11,0 11,1 11,2 Sayama, pp. 287-289
- ↑ Sayama, p. 124
- ↑ Week 13, MCB111: Mathematics in Biology (Fall 2021)
- ↑ Gros, p. 115
- ↑ 15,0 15,1 Sayama, p. 268
- ↑ 16,0 16,1 Pearson's Classification (Extended) of Gray-Scott System Parameter Values
Bibliografia principal
- C. Gros, "Complex and Adaptive Dynamical Systems". Springer-Verlag, Berlim, 2015.
- H. Sayama, "Introduction to the Modeling and Analysis of Complex Systems". Open SUNY Textbooks, Geneseo, NY, 2015.



















































![{\displaystyle \Delta _{i}:=\operatorname {det} \left(J_{R}(u_{i}^{*},v_{i}^{*})\right)=(F+k)\left[(v_{i}^{*})^{2}-F\right]\quad (10)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d30ce1b2dd5a0638ce7860d81732fa18fab8be48)

![{\displaystyle {\frac {\Delta _{i}}{F(F+k)}}={\frac {(v_{i}^{*})^{2}}{F}}-1=\left[{\frac {1\mp {\sqrt {1-4(\gamma {\sqrt {F}})^{2}}}}{2(\gamma {\sqrt {F}})}}\right]^{2}-1=\left[{\frac {1\mp {\sqrt {1-4a^{2}}}}{2a}}\right]^{2}-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6dc4e89a50fb14385e69f7ae2244be3caa56cfa)















































![{\displaystyle \nabla ^{2}f(x,y,t)\approx {\frac {1}{\Delta h^{2}}}\left[f(x+\Delta h,y,t)+f(x-\Delta h,y,t)+f(x,y+\Delta h,t)+f(x,y-\Delta h,t)-4f(x,y,t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7119cf33bdfa46db2adc9177482f8bd3a1178cc7)




![{\displaystyle {\begin{aligned}u_{i,j}^{n+1}=u_{i,j}^{n}&+\left[-u_{i,j}^{n}(v_{i,j}^{n})^{2}+F(1-u_{i,j}^{n})+D_{u}{\frac {u_{i+1,j}^{n}+u_{i-1,j}^{n}+u_{i,j+1}^{n}+u_{i,j-1}^{n}-4u_{i,j}^{n}}{\Delta h^{2}}}\right]\Delta t\\v_{i,j}^{n+1}=v_{i,j}^{n}&+\left[u_{i,j}^{n}(v_{i,j}^{n})^{2}-(F+k)v_{i,j}^{n}+D_{v}{\frac {v_{i+1,j}^{n}+v_{i-1,j}^{n}+v_{i,j+1}^{n}+v_{i,j-1}^{n}-4v_{i,j}^{n}}{\Delta h^{2}}}\right]\Delta t\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd9ff0cba26c1af6ff749b825b7b81edc1693093)













































