Mudanças entre as edições de "Algoritmo de Wang-Landau"
(Criou página com ' ==Introdução== Ao contrário dos métodos convencionais de Monte Carlo, que geram diretamente uma distribuição canônica <math>g(E) e^{-E/k_B T}</math> a uma dada tempera...') |
(→Resultados) |
||
| Linha 27: | Linha 27: | ||
====Implementação==== | ====Implementação==== | ||
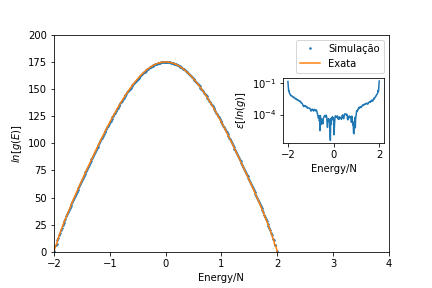
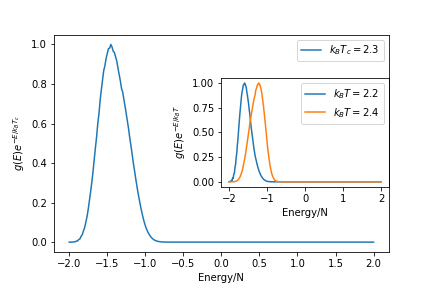
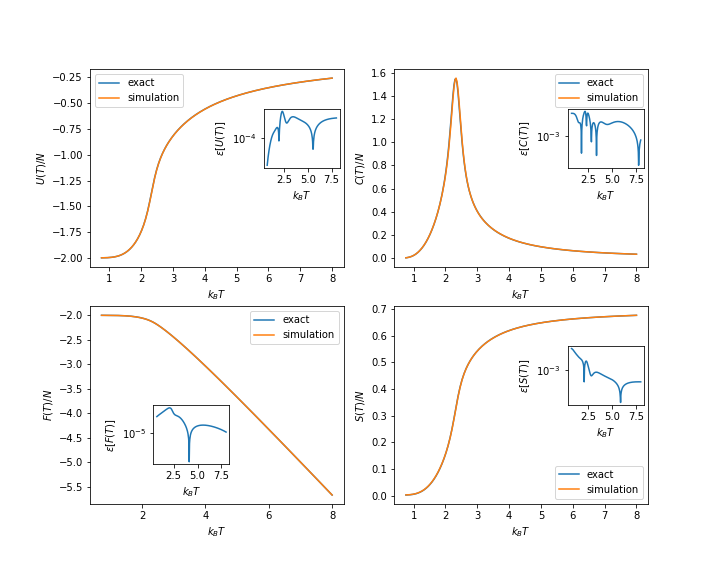
====Resultados==== | ====Resultados==== | ||
| + | |||
| + | [[Arquivo:fig1.png]] | ||
| + | [[Arquivo:fig2.png]] | ||
| + | [[Arquivo:fig3.png]] | ||
Edição das 14h06min de 28 de novembro de 2021
Índice
Introdução
Ao contrário dos métodos convencionais de Monte Carlo, que geram diretamente uma distribuição canônica 
a uma dada temperatura 
, a abordagem de Wang-Landau estima a densidade de estados 
diretamente por meio de um passeio aleatório, que produz um histograma plano no espaço de energia 
.
Algoritmo
No início da simulação, é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir 
para todas as energias possíveis 
. A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando aleatoriamente seu estado.
Cada vez que uma energia é visitada, a entrada correspondente em é incrementada em 1. A estimativa de é então modificada por um fator multiplicativo 
, e o valor atualizado realiza um passeio aleatório adicional no espaço de .
Se 
e 
são energias antes e depois de um valor de spin ser alterado, a probabilidade de transição da energia para é
A razão das probabilidades de transição de para e de a podem ser calculados como
Logo, o algoritmo de passeio aleatório satisfaz o equilíbrio detalhado:
onde 
é a probabilidade na energia e 
é a probabilidade de transição de para .
Aplicação ao Modelo de Ising 2D
Modelo de Ising
Implementação
Resultados
