Algoritmo de Wang-Landau

Nomes: Rafael Abel da Silveira e William Machado Pantaleão

Introdução

Simulações computacionais, como o método de Monte Carlo, são vastamente utilizadas para estudar transições de fase e fenômenos críticos. O método padrão para simulações de Monte Carlo é o algoritmo de Metropolis, entretanto, algoritmos novos e mais eficientes são usados em simulações modernas, como o algoritmo de Wang-Landau. Ao contrário dos métodos convencionais de Monte Carlo, que geram diretamente uma distribuição canônica $g(E)e^{-E/k_{B}T}$ a uma dada temperatura $T$ , a abordagem de Wang-Landau estima a densidade de estados $g(E)$ diretamente por meio de um passeio aleatório, que produz um histograma plano no espaço de energia $H(E)$ . ^[1]

Mesmo para modelos que podem ser resolvidos analiticamente, a densidade de estados $g(E)$ não pode ser determinada para sistemas maiores ^[2]. Com o algoritmo de Wang-Landau, é possível obter a $g(E)$ a partir de um passeio aleatório. A estimativa para $g(E)$ é melhorada a cada etapa do passeio aleatório, usando um fator de modificação $f$ cuidadosamente controlado, para produzir um resultado que converge para o valor real rapidamente.

Amostragem de Wang-Landau

No início da simulação, $g(E)$ é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir $g(E)=1$ para todas as energias possíveis $E$ . A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando seu estado (single-spin flip).

Cada vez que uma energia $E$ é visitada, o histograma $H(E)$ é incrementado em 1. A estimativa de $g(E)$ é então modificada por um fator multiplicativo $f$ , e o valor atualizado realiza um passeio aleatório adicional no espaço de $E$ .

Se $E_{1}$ e $E_{2}$ são as energias antes e depois de um valor de spin ser alterado, a probabilidade de transição da energia $E_{1}$ para $E_{2}$ é dada por

$p(E_{1}\rightarrow E_{2})=min\left({\frac {g(E_{1})}{g(E_{2})}},1\right).$

A razão das probabilidades de transição de $E_{1}$ para $E_{2}$ e de $E_{2}$ a $E_{1}$ podem ser calculados como

${\frac {p(E_{1}\rightarrow E_{2})}{p(E_{2}\rightarrow E_{1})}}={\frac {g(E_{1})}{g(E_{2})}}.$

Logo, o algoritmo de passeio aleatório satisfaz o balanço detalhado no limite em que $f\to 1$ :

${\frac {1}{g(E_{1})}}p(E_{1}\rightarrow E_{2})={\frac {1}{g(E_{2})}}p(E_{2}\rightarrow E_{1}),$

onde $1/g(E_{1})$ é a probabilidade na energia $E_{1}$ e $p(E_{1}\rightarrow E_{2})$ é a probabilidade de transição de $E_{1}$ para $E_{2}$ .

Se o estado de energia $E_{2}$ é aceito, a densidade de estados $g(E_{2})$ é multiplicada pelo fator de modificação $f>1$ de maneira que $g(E_{2})\to f\times g(E_{2})$ e a entrada no histograma para $H(E_{2})$ é atualizada de forma $H(E_{2})\to H(E_{2})+1$ . Se o estado de energia não é aceito, a densidade de estados $g(E_{1})$ é multiplicada pelo fator de modificação, $g(E_{1})\to f\times g(E_{1})$ e $H(E_{1})$ é atualizada de forma $H(E_{1})\to H(E_{1})+1$ .

Flatness

O procedimento de passeio aleatório é seguido até o histograma $H(E)$ estar plano (do inglês, "flat"), e para determinar isso, a cada $n$ iterações verificamos se todos valores possíveis de $E$ estão a uma distância, no máximo, $x\%$ de $\langle H(E)\rangle$ . A variável $x$ é denominada "flatness". Quando o histograma está plano, todos estados de energia foram visitados muitas vezes.

O número de passos, $n$ que devemos realizar antes de checar deve ser maior que $L^{2}$ onde $L$ indica o tamanho da rede, para que o algoritmo tenha a oportunidade de visitar cada estado várias vezes.

Para sistemas simples, podemos utilizar um valor tão alto quanto 95%, entretanto, para este trabalho foi escolhido o valor de 80%.

Fator de modificação

Em geral, como $g(E)$ se torna muito grande, trabalhamos com o logaritmo natural dessas quantidades, $\ln g(E)$ . Portanto, cada atualização da densidade de estados é dada por $\ln g(E)\to \ln g(E)+\ln f$ . O valor comumente utilizado para o fator de modificação é $f=f_{0}=e$ .

Quando o histograma é considerado plano, pelas condições descritas acima, reduzimos o valor de $f$ de forma que o novo valor será $f_{1}={\sqrt {f_{0}}}$ , resetamos o histograma $H(E)$ e recomeçamos o passeio aleatório.

A simulação é parada para um valor de $f$ predeterminado. No caso, usamos $f_{final}=\exp(10^{-8})=1.00000001$ .

Aplicação ao Modelo de Ising 2D

Modelo de Ising

O modelo de Ising é uma rede 2D, de tamanho $L\times L$ que consiste de uma variável discreta em cada sítio que pode ser usada para representar o momento de dipolo magnético de um átomo^[3] Cada sítio pode ter o valor de spin $+1$ ou $-1$ .

Para este trabalho, o hamiltoniano de interação pode ser calculado por ${\mathcal {H}}=-\sum _{\langle i,j\rangle }\sigma _{i}\sigma _{j}$ onde $\langle i,j\rangle$ indica pares distintos de vizinhos-mais-próximos.

Com a densidade de estados, podemos calcular as seguintes quantidades termodinâmicas:

Energia interna:

$U(T)={\frac {\sum _{E}Eg(E)e^{-E/k_{B}T}}{\sum _{E}g(E)e^{-E/k_{B}T}}}=\langle E\rangle$

Calor específico:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C(T) = \frac{\partial U(T)}{\partial T} = \frac{\langle E^2 \rangle - \langle E \rangle ^2}{k_BT^2} }

Energia livre de Helmoltz:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(T) = -k_BT\ln\left( \sum_E g(E) e^{-E/k_BT} \right) }

Entropia:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(T) = \frac{U(T) - F(T)}{T} }

Finalmente, podemos também calcular a distribuição canônica usando:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E,T) = g(E) e^{-E/k_BT} }

Algoritmo

Resumindo, o passo a passo do algoritmo pode ser escrito como:

1. Defino Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(E) = 1} para todos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E } e o fator de modificação inicial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_0 = e} ;

2. Aleatoriamente, escolho um spin e troco o seu valor. Aceito a transição com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(E_1 \to E_2) = \min (g(E_1)/g(E_2), 1) } ;

3. Modifico a densidade de estados Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(E) \to g(E) \times f } e atualizo o histograma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(E)} ;

4. Continuo até o histograma estar plano, então diminuo o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} , fazendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1 = \sqrt{f_0} } e reseto o histograma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(E)} ;

5. Repito os passos 2-4 até Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f < 1.00000001 } .

6. Obtendo a $g(E)$ , posso calcular as quantidades termodinâmicas descritas anteriormente.

Resultados

Densidade de estados

A estimativa da densidade de estados para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 16} usando a amostragem de Wang-Landau é mostrada na Fig. 1, junto com os resultados exatos de Beale ^[2].

Os fatores de modificação inicial e final para os passeios aleatórios foram Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ln(f_0) = 1 e \ln(f_{final}) = 10^{−8} } .

O histograma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(E)} foi considerado plano quando todas as entradas não eram inferiores a 80% da média Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle H(E)\rangle } .

A densidade absoluta de estados na Fig. 1 é obtida pela condição de que o número de estados fundamentais seja 2 para o modelo de Ising 2D.

Com a escala logarítmica usada na Fig. 1, os dados simulados e a solução exata se sobrepõem perfeitamente. Na inserção da Fig. 1, vemos que o erro relativo é, de fato, muito pequeno.

Figura 1: Logaritmo da densidade de estados Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln g(E) } do modelo de Ising 2D com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 16 } .

Distribuição canônica

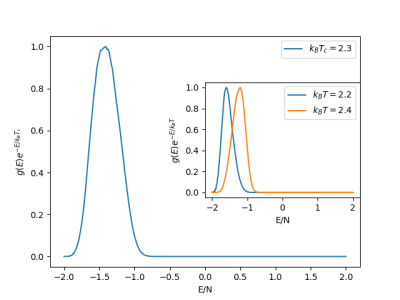
Podemos calcular a distribuição canônica usando a equação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E, T) = g(E)e^{−E/k_BT}} a qualquer temperatura, sem a necessidade de realizar várias simulações.

Na Fig. 2, mostramos a distribuição canônica resultante na temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} , que exibe um único pico.

Figura 2: Distribuição canônica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E,T_c) = g(E)e^{-E/k_BT_c} } na temperatura de transição do modelo de Ising 2D com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 16 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_BT_c = 2.3 } .

As distribuições em temperaturas acima e abaixo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} também apresentam pico único, conforme ilustrado no detalhe da Fig. 3.

Figura 3: Distribuição canônica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E,T) = g(E)e^{-E/k_BT} } nas temperaturas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 2.2 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 2.4 } do modelo de Ising 2D com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 16 } .

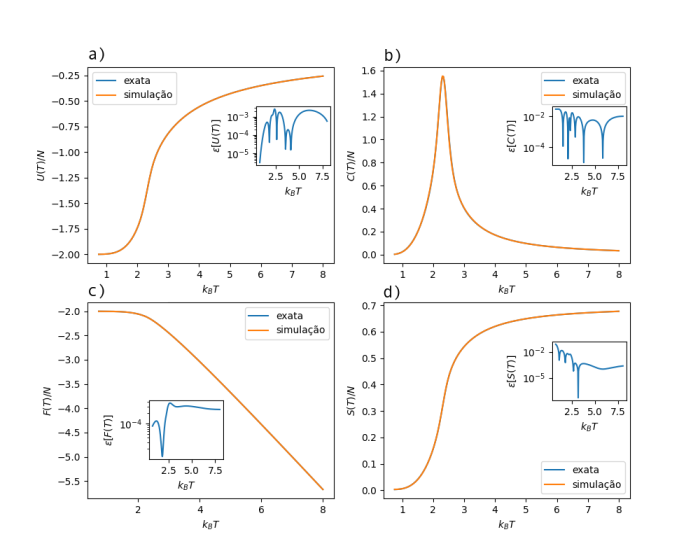
Quantidades termodinâmicas

Os resultados simulados, calculados diretamente com as equações descritas no capítulo anterior, e as soluções exatas se sobrepõem quase perfeitamente em uma ampla região de temperatura de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_BT = 0 - 8} .

Testes mais rigorosos de precisão são fornecidos a partir dos erros relativos para as respectivas quantidades termodinâmicas. Os erros relativos são muito pequenos para toda a região de temperatura de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_BT = 0 - 8} .

Como o sistema tem uma transição de fase de segunda ordem, a primeira derivada da energia livre é uma função contínua da temperatura. Não há saltos na energia interna ou na entropia, mesmo no limite em que o tamanho do sistema vai para o infinito.

Figura 4: Quantidades termodinâmicas do modelo de Ising 2D com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = 16 } calculado a partir da densidade de estados

g(E)

. Na figura, estão mostrados: (a) energia interna, (b) calor específico, (c) energia livre de Helmholtz e (d) entropia. Os gráficos inset são os erros relativos.

Magnetização

Na presença de um campo magnético externo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} , o hamiltoniano do modelo de Ising 2D é dado por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} =-\sum_{\langle i,j\rangle} \sigma_i \sigma_j - h \sum_{i=1} \sigma_i} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M' = \sum_{i=1} \sigma_i } é a magnetização e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E' =-\sum_{\langle i,j\rangle} \sigma_i \sigma_j } é a energia de troca.

A diferença para o algoritmo anterior é que o passeio aleatório agora é executando tanto na energia Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E' } quanto no parâmetro de ordem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M' } , e um histograma 2D Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(E',M') } é acumulado.

A função de partição pode ser calculada como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z(T,h)=\sum_{E',M'}g(E',M')e^{-(E'-hM')/k_BT} } e, a parir dela, podemos obter quantidades termodinâmicas para todos os valores de temperatura e campo magnético.

Ainda, a magnetização média do sistema é dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(T,h) = \frac{\sum_{E',M'}M'g(E',M')e^{-(E'-hM')/k_BT}}{\sum_{E',M'}g(E',M')e^{-(E'-hM')/k_BT}} } .

Conclusões

O algoritmo de Wang-Landau é uma ferramenta eficiente para o cálculo direto da densidade de estados para grandes sistemas. A alta precisão do método se dá pela modificação da estimativa em cada etapa do passeio aleatório no espaço de energia Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E } e pelo controle cuidadoso do fator de modificação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } .

Diferentemente das simulações convencionais de MC, quantidades termodinâmicas como a energia livre de Helmholtz estão diretamente disponíveis uma vez que, usando a densidade de estados, essas quantidades podem ser calculadas essencialmente a qualquer temperatura.

É importante ressaltar que o método de Wang-Landau não está limitado ao passeio aleatório no espaço de energia ou a modelos simples em redes pequenas. Ele pode ser aplicado a qualquer parâmetro e também se mostra eficiente para sistemas grandes, como sistemas complexos gerais com paisagens irregulares.

Código

from scipy import *
import sys
import numpy as np
from pylab import *
from matplotlib import pyplot as plt

#Rede aleatória para Ising 2D
def redeAleatoria(L):
    latt=zeros((L,L),dtype=int)
    for i in range(L):
        for j in range(L):
            latt[i,j]=sign(2*rand()-1)
    return latt
    
#Energia da rede
def energia(latt):
    Ene=0
    for i in range(L):
        for j in range(L):
            S=latt[i,j]
            WF=latt[(i+1)%L,j]+latt[i,(j+1)%L]+latt[(i-1)%L,j]+latt[i,(j-1)%L]
            Ene+=-WF*S
    return int(Ene/2.)
    
#Quantidades termodinâmicas usando a densidade de estados
def quantTermod(T,lngE,Energies,E0):
    Z=0
    Ev=0
    E2v=0
    for i,E in enumerate(Energies):
        w=exp(lngE[i]-E/T)
        Z+=w
        Ev+=w*E
        E2v+=w*E**2
    Ev*=1./Z
    cv=(E2v/Z-Ev**2)/T**2
    F = -T*np.log(Z)
    S = (Ev - F)/T
    return (Ev/N,cv/N,F/N,S/N)
    
#Algoritmo de Wang-Landau
def WangLandau(L,N,indices,E0,flatness,fmin):
    latt=redeAleatoria(L)
    Ene=energia(latt)
    lngE=zeros(len(Energies),dtype=float)
    Hist=zeros(len(Energies),dtype=float)
    lnf=1.0
    itt = 0
    while exp(lnf) > fmin:
        itt = itt + 1
        ii=int(rand()*N)       
        (i,j)=(ii%L,ii/L) 
        i=int(rand()*L)
        j=int(rand()*L)
        S=latt[i,j] 
        WF=latt[(i+1)%L,j]+latt[i,(j+1)%L]+latt[(i-1)%L,j]+latt[i,(j-1)%L]
        Enew=Ene+2*S*WF
        P=exp(lngE[indices[Ene+E0]]-lngE[indices[Enew+E0]])
        if P>rand():   
            latt[i,j]=-S        
            Ene=Enew       
        Hist[indices[Ene+E0]]+=1.
        lngE[indices[Ene+E0]]+=lnf
        if itt%1000==0:
            aH=sum(Hist)/(N) 
            mH=min(Hist)          
            if mH>aH*flatness:  
                Hist=zeros(len(Hist)) 
                lnf/=2.             
                print("iteracao =", itt, 'f=', exp(lnf))
    return lngE,Hist
    


fmin = 1.00000001
print(fmin)
L=16
flatness=0.8
N=L*L

# energias possiveis
Energies = (4*arange(N+1)-2*N).tolist()
print(Energies)
Energies.pop(1)   
Energies.pop(-2)
E0=Energies[-1]
print(Energies)                      
indices=-ones(E0*2+1,dtype=int)

for i,E in enumerate(Energies):
  indices[E+E0]=i

(lngE, Hist) = WangLandau(L, N, indices, E0, flatness, fmin)

Hist *= len(Hist)/sum(Hist)

len(lngE),len(Hist)

from pylab import *
EE=array(Energies);EE=EE/(L*L)
plt.plot(EE,lngE,'o',markersize=1.5,label='Simulação')
#plt.plot(EE,Hist,'-s',markersize=2.0,label='Histogram')
xlabel(r'$E/N$')
ylabel(r'$ln[g(E)]$')
legend(loc='best')
show()

f=open('bealeL16.dat','r');f=f.readlines()

beale=[]
for i in range(len(f)):
  beale.append(float(f[i]))

plt.plot(Energies,beale,label='Exata')
xlabel('Energia')
ylabel('ln[g(E)]')
legend(loc='best')
show()

plt.plot(EE,beale,label='Exata')
plt.plot(EE,lngE,'o',markersize=1.5,label='Simulação')
xlabel(r'$E/N$')
ylabel(r'$ln[g(E)]$')
legend(loc='best')
show()

#Erro relativo

erro=[]
for i in range(len(lngE)):
  erro.append((abs(lngE[i]-beale[i]))/beale[i])

plt.plot(Energies,erro)
xlabel('Energia')
ylabel(r'$\epsilon [ln(g)]$')
#legend(loc='best')
yscale('log')
show()

from mpl_toolkits.axes_grid.inset_locator import (inset_axes,InsetPosition,mark_inset)

fig,ax1=subplots()
ax1.plot(EE,lngE,'o',markersize=1.5,label='Simulação')
ax1.plot(EE,beale,label='Exata')
ax1.set_xlabel('E/N')
ax1.set_ylabel(r'$ln[g(E)]$')
ax1.set_xlim(-2.,4.)
ax1.set_ylim(0.,200.)
ax1.legend(loc='best')
ax2=axes([0,0,1,1])
ip=InsetPosition(ax1,[0.685,0.5,0.3,0.3])
ax2.set_axes_locator(ip)
ax2.plot(EE,erro)
ax2.set_yscale('log')
ax2.set_xlabel('E/N')
ax2.set_ylabel(r'$\epsilon [ln(g)]$')
savefig('fig1.png')
show()

print(beale[0:5])

print(lngE[0:5])

lmb23 = -1**300
lmb23e = -1**300

i=0
while i<N-1:
  termo23 = lngE[i] - Energies[i]/2.3
  if termo23 > lmb23:
    lmb23 = termo23
  i = i+1

i=0
while i<N-1:
  termo23e = beale[i] - Energies[i]/2.3
  if termo23e > lmb23e:
    lmb23e = termo23e
  i = i+1

print(lmb23,lmb23e)

lmb22 = -1**300
lmb22e = -1**300
lmb24 = -1**300
lmb24e = -1**300

i=0
while i<N-1:
  termo22 = lngE[i] - Energies[i]/2.2
  if termo22 > lmb22:
    lmb22 = termo22
  i = i+1

i=0
while i<N-1:
  termo22e = beale[i] - Energies[i]/2.2
  if termo22e > lmb22e:
    lmb22e = termo22e
  i = i+1

i=0
while i<N-1:
  termo24 = lngE[i] - Energies[i]/2.4
  if termo24 > lmb24:
    lmb24 = termo24
  i = i+1

i=0
while i<N-1:
  termo24e = beale[i] - Energies[i]/2.4
  if termo24e > lmb24e:
    lmb24e = termo24e
  i = i+1

print(lmb22,lmb22e,lmb24,lmb24e)

E=array(Energies);E1=E/N
P=exp(lngE-E/2.3 - lmb23)
Pexact=exp(beale-E/2.3 - lmb23e)


plt.plot(E1,P,label=r'$k_B T_c = 2.3$')
plt.plot(E1,Pexact,label=r'$k_B T_c = 2.3$ exata')
#plt.plot(Energies,P2,label=r'$k_B T_c = 2.2$')
#plt.plot(Energies,P3,label=r'$k_B T_c = 2.4$')
xlabel('E/N')
ylabel(r'$g(E)e^{-E/k_B T_c}$')
legend(loc='best')
show()

P2=exp(lngE-E/2.2-lmb22)
P2exact=exp(beale-E/2.2-lmb22e)
P3=exp(lngE-E/2.4-lmb24)
P3exact=exp(beale-E/2.4-lmb24e)

fig,ax1=subplots()
ax1.plot(E1,P,label=r'$k_B T_c = 2.3$')
#ax1.plot(E1,Pexact,label=r'$k_B T_c = 2.3$ exata')
ax1.set_xlabel('E/N')
ax1.set_ylabel(r'$g(E)e^{-E/k_B T_c}$')
#ax1.set_ylim(0.,200.)
ax1.legend(loc='best')
ax2=axes([0,0,1,1])
ip=InsetPosition(ax1,[0.5,0.3,0.5,0.5])
ax2.set_axes_locator(ip)
ax2.plot(E1,P2,label=r'$k_B T = 2.2$')
#ax2.plot(E1,P2exact,label=r'$k_B T = 2.2$ exata')
ax2.plot(E1,P3,label=r'$k_B T = 2.4$')
#ax2.plot(E1,P3exact,label=r'$k_B T = 2.4$ exata')
#ax2.set_yscale('log')
ax2.set_xlabel('E/N')
ax2.set_ylabel(r'$g(E)e^{-E/k_B T}$')
ax2.legend(loc='best')
savefig('fig2.png')
show()

E=array(Energies);E1=E/N
P=exp(lngE-E/2.3 - lmb23)
Pexact=exp(beale-E/2.3 - lmb23e)


plt.plot(E1,P,label=r'$k_B T_c = 2.3$')
plt.plot(E1,Pexact,label=r'$k_B T_c = 2.3$ exata')
#plt.plot(Energies,P2,label=r'$k_B T_c = 2.2$')
#plt.plot(Energies,P3,label=r'$k_B T_c = 2.4$')
xlabel('E/N')
ylabel(r'$g(E)e^{-E/k_B T_c}$')
legend(loc='best')
show()

lmb22 = -1**300
lmb22e = -1**300
lmb24 = -1**300
lmb24e = -1**300

i=0
while i<N-1:
  termo22 = lngE[i] - Energies[i]/2.2
  if termo22 > lmb22:
    lmb22 = termo22
  i = i+1

i=0
while i<N-1:
  termo22e = beale[i] - Energies[i]/2.2
  if termo22e > lmb22e:
    lmb22e = termo22e
  i = i+1

i=0
while i<N-1:
  termo24 = lngE[i] - Energies[i]/2.4
  if termo24 > lmb24:
    lmb24 = termo24
  i = i+1

i=0
while i<N-1:
  termo24e = beale[i] - Energies[i]/2.4
  if termo24e > lmb24e:
    lmb24e = termo24e
  i = i+1

print(lmb22,lmb22e,lmb24,lmb24e)

P2=exp(lngE-E/2.2-lmb22)
P2exact=exp(beale-E/2.2-lmb22e)
P3=exp(lngE-E/2.4-lmb24)
P3exact=exp(beale-E/2.4-lmb24e)

fig,ax1=subplots()
ax1.plot(E1,P,label=r'$k_B T_c = 2.3$')
#ax1.plot(E1,Pexact,label=r'$k_B T_c = 2.3$ exata')
ax1.set_xlabel('E/N')
ax1.set_ylabel(r'$g(E)e^{-E/k_B T_c}$')
#ax1.set_ylim(0.,200.)
ax1.legend(loc='best')
ax2=axes([0,0,1,1])
ip=InsetPosition(ax1,[0.5,0.3,0.5,0.5])
ax2.set_axes_locator(ip)
ax2.plot(E1,P2,label=r'$k_B T = 2.2$')
#ax2.plot(E1,P2exact,label=r'$k_B T = 2.2$ exata')
ax2.plot(E1,P3,label=r'$k_B T = 2.4$')
#ax2.plot(E1,P3exact,label=r'$k_B T = 2.4$ exata')
#ax2.set_yscale('log')
ax2.set_xlabel('E/N')
ax2.set_ylabel(r'$g(E)e^{-E/k_B T}$')
ax2.legend(loc='best')
savefig('fig2.png')
show()

Te = linspace(0,8,255)
Thm=[];Thm_exact=[]

for T in Te:
  Thm.append(quantTermod(T, lngE, Energies, E0))
  Thm_exact.append(quantTermod(T, beale, Energies, E0))

Thm = array(Thm)
Thm_exact=array(Thm_exact)

#Energia interna
plt.plot(Te,Thm_exact[:,0],label='exata')
plt.plot(Te,Thm[:,0],label='simulação')
plt.xlabel(r'$k_B T$')
plt.ylabel(r'$U(T)/N$')
plt.legend(loc='best')
plt.show()

#Calor específico
plt.plot(Te,Thm_exact[:,1],label='exata')
plt.plot(Te,Thm[:,1],label='simulação')
plt.xlabel(r'$k_B T$')
plt.ylabel(r'$C(T)/N$')
plt.legend(loc='best')
plt.show()

#Energia livre de Helmholtz
plt.plot(Te,Thm_exact[:,2],label='exata')
plt.plot(Te,Thm[:,2],label='simulação')
plt.xlabel(r'$k_B T$')
plt.ylabel(r'$F(T)/N$')
plt.legend(loc='best')
plt.show()

#Entropia
plt.plot(Te,Thm_exact[:,3],label='exata')
plt.plot(Te,Thm[:,3],label='simulação')
plt.xlabel(r'$k_B T$')
plt.ylabel(r'$S(T)/N$')
plt.legend(loc='best')
plt.show()

erroUt=(abs(Thm[:,0]-Thm_exact[:,0]))/abs(Thm_exact[:,0])
erroCt=(abs(Thm[:,1]-Thm_exact[:,1]))/Thm_exact[:,1]
erroFt=(abs(Thm[:,2]-Thm_exact[:,2]))/abs(Thm_exact[:,2])
erroSt=(abs(Thm[:,3]-Thm_exact[:,3]))/Thm_exact[:,3]

#Erro relativo para energia interna
plt.plot(Te,erroUt)
xlabel(r'$k_B T$')
ylabel(r'$\epsilon [U(T)]$')
yscale('log')
plt.show()

#Erro relativo para calor específico
plt.plot(Te,erroCt)
xlabel(r'$k_B T$')
ylabel(r'$\epsilon [C(T)]$')
yscale('log')
plt.show()

#Erro relativo para energia livre de Helmholtz
plt.plot(Te,erroFt)
xlabel(r'$k_B T$')
ylabel(r'$\epsilon [F(T)]$')
yscale('log')
plt.show()

#Erro relativo para entropia
plt.plot(Te,erroSt)
xlabel(r'$k_B T$')
ylabel(r'$\epsilon [S(T)]$')
yscale('log')
plt.show()

figure(figsize=(10,8))

ax1=subplot(2,2,1)
ax1.plot(Te,Thm_exact[:,0],label='exata')
ax1.plot(Te,Thm[:,0],label='simulação')
ax1.set_xlabel(r'$k_B T$')
ax1.set_ylabel(r'$U(T)/N$')
ax1.legend(loc='best')
ax12=axes([1,0,0,0])
ip=InsetPosition(ax1,[0.685,0.5,0.3,0.3])
ax12.set_axes_locator(ip)
ax12.plot(Te,erroUt)
ax12.set_yscale('log')
ax12.set_xlabel(r'$k_B T$')
ax12.set_ylabel(r'$\epsilon [U(T)]$')

ax2=subplot(2,2,2)
ax2.plot(Te,Thm_exact[:,1],label='exata')
ax2.plot(Te,Thm[:,1],label='simulação')
ax2.set_xlabel(r'$k_B T$')
ax2.set_ylabel(r'$C(T)/N$')
ax2.legend(loc='best')
ax22=axes([0,1,0,0])
ip=InsetPosition(ax2,[0.685,0.5,0.3,0.3])
ax22.set_axes_locator(ip)
ax22.plot(Te,erroCt)
ax22.set_yscale('log')
ax22.set_xlabel(r'$k_B T$')
ax22.set_ylabel(r'$\epsilon [C(T)]$')

ax3=subplot(2,2,3)
ax3.plot(Te,Thm_exact[:,2],label='exata')
ax3.plot(Te,Thm[:,2],label='simulação')
ax3.set_xlabel(r'$k_B T$')
ax3.set_ylabel(r'$F(T)/N$')
ax3.legend(loc='best')
ax32=axes([0,0,1,0])
ip=InsetPosition(ax3,[0.25,0.2,0.3,0.3])
ax32.set_axes_locator(ip)
ax32.plot(Te,erroFt)
ax32.set_yscale('log')
ax32.set_xlabel(r'$k_B T$')
ax32.set_ylabel(r'$\epsilon [F(T)]$')

ax4=subplot(2,2,4)
ax4.plot(Te,Thm_exact[:,3],label='exata')
ax4.plot(Te,Thm[:,3],label='simulação')
ax4.set_xlabel(r'$k_B T$')
ax4.set_ylabel(r'$S(T)/N$')
ax4.legend(loc='best')
ax42=axes([0,0,0,1])
ip=InsetPosition(ax4,[0.685,0.5,0.3,0.3])
ax42.set_axes_locator(ip)
ax42.plot(Te,erroSt)
ax42.set_yscale('log')
ax42.set_xlabel(r'$k_B T$')
ax42.set_ylabel(r'$\epsilon [S(T)]$')
savefig('fig3.png')
show()

Referências

↑ D. P. Landau, Shan-ho Tsai, M. Exler, A new approach to Monte Carlo simulations in statistical physics: Wang-Landau sampling, American Journal of Physics 72, 1294 (2004). https://doi.org/10.1119/1.1707017
↑ ^2,0 ^2,1 P. D. Beale, Exact Distribution of Energies in the Two-Dimensional Ising Model, Phys. Rev. Lett. 76,78 (1996). https://doi.org/10.1103/PhysRevLett.76.78
↑ A. Rosa, C. Pires, L. Doria, Ising 2D, Wiki da Física Computacional da UFRGS. https://fiscomp.if.ufrgs.br/index.php/Ising_2D#Modelo_de_Ising

[wanglandau-1] D. P. Landau, Shan-ho Tsai, M. Exler, A new approach to Monte Carlo simulations in statistical physics: Wang-Landau sampling, American Journal of Physics 72, 1294 (2004). https://doi.org/10.1119/1.1707017

[beale-2] 2,0 ^2,1 P. D. Beale, Exact Distribution of Energies in the Two-Dimensional Ising Model, Phys. Rev. Lett. 76,78 (1996). https://doi.org/10.1103/PhysRevLett.76.78

[ising-3] A. Rosa, C. Pires, L. Doria, Ising 2D, Wiki da Física Computacional da UFRGS. https://fiscomp.if.ufrgs.br/index.php/Ising_2D#Modelo_de_Ising

[1]

[2]

[3]

Algoritmo de Wang-Landau

Índice

Introdução