Modelos Logísticos

Anterior: Modelo de Levins | Índice: Ecologia | Próximo: AC: Jogo da Vida

Modelo logístico simples

A equação logística pode ser escrita da seguinte forma:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dN}{dt}=rN\left[1-\frac{N}{K}\right]}

Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle K} são as constantes de crescimento e de suporte respectivamente, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N} é a densidade populacional que tem como variável independente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t} . Há dois estados de equilíbrio: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N_{1}=0} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle ,N_{2}=K} . Linearizando o sistema próximo do primeiro ponto de equilíbrio conforme pode ser visto em Linearização de sistemas de equações não lineares, calculando o único termo da matriz jacobiana:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\dot{N}}{dN}|_{N=0}=r}

Logo o sistema linearizado próximo ao ponto de equilíbrio é:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{N} & =\left(\frac{d\dot{N}}{dN}|_{N=0}\right)\left(N\right)\\ & =rN\end{align}}

Temos simplesmente que se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r>0} , então é um ponto de equilíbrio instável. Realizando o mesmo procedimento para analisar na vizinhança do segundo ponto:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{N} & =\left(\frac{d\dot{N}}{dN}|_{N=K}\right)\left(N\right)\\ & =-rN\end{align}}

Então se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r>0} , este ponto é estável. Como usa-se uma constante de crescimento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r>0} , o sistema evolui até atingir o ponto de equilíbrio de saturação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=K} . A solução pode ser obtida através do uso do Mathematica:

parametros = Rationalize[{r -> 1, k -> 1}];
sol = NDSolve[{n'[t] == r*n[t]*(1 - n[t]/k) /. parametros,
      n[0] == 0.5}, n, {t, 0, tmax}];
Plot[n[t] /. sol, {t, 0, tmax}]

Modelo logístico atrasado

A equação logística assume que a taxa de variação da população dos organismos depende instantaneamente das variações no tamanho da população, porém em muitos casos, pode haver um atraso. Por exemplo, populações que armazenam nutrientes, podem não sofrer imediatamente os efeitos, mesmo se a população se tornar muito grande para a quantidade de recursos disponíveis. Por isso a equação logística pode incorporar um atraso na sua taxa de variação da seguinte maneira:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dN\left(t\right)}{dt}=rN\left(t\right)\left(1-\frac{N\left(t-\tau\right)}{K}\right)}

Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \tau} é o Atraso. Para facilitar, denotando então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N=N\left(t\right)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N_{\tau}=N\left(1-\tau\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{N}=rN\left(1-\frac{N_{\tau}}{K}\right)}

Observação: As constantes poderiam ser simplificadas realizando a substituição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle y\left(t\right)=\frac{N\left(t\right)}{K}} , de forma que restaria apenas a constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha\equiv r\tau} . Vale a pena ressaltar que esta equação exige que para as condições iniciais seja especificado o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N} sobre todo o intervalo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left[0,\tau\right]} . Frequentemente isso é feito considerando que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N} é constante no intervalo, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N=N_{0}} para todo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle t\in\left[0,\tau\right]} . Para encontrar o equilíbrio analiticamente, tem-se então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N=N_{\tau}} , uma vez que no equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N} não deve variar no tempo, dessa maneira o valor para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N} deve ser o mesmo, com ou sem atraso. Então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0=rN\left(1-\frac{N}{K}\right)}

Os mesmos pontos de equilíbrio discutidos anteriormente são recuperados: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N_{1}=0} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N_{2}=K} . Plotando para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle k=\tau=1} , e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r=1.5} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r=1.6} tem-se:

Soluções numéricas do sistema. Na esquerda superior a solução para a equação logística simples com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r>0} , na direita superior a solução para a equação logística com atraso para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=\tau=1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=1.5} . E embaixo também a equação logística com atraso porém para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=1.6} .

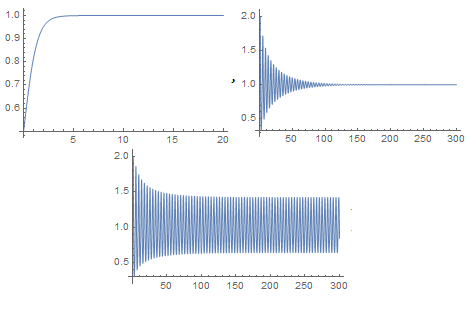
Verifica-se a existência de uma bifurcação de Hopf entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r=1.5} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle r=1.6} , isto é, um ponto crítico no qual a estabilidade do sistema sofre uma mudança e uma solução periódica surge. Então um modelo de população com uma única espécie ainda pode ter um comportamento oscilatório. Para analisar o ponto de equilíbrio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N=K} , pode-se introduzir uma pequena perturbação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u} e verificar se o ponto no espaço de fase retorna ao ponto de equilíbrio. Então sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle N\left(t\right)=K+u\left(t\right)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \dot{N} & =rN\left(1-\frac{N_{\tau}}{K}\right)\\ \dot{u} & =r\left(K+u\right)\left(1-\frac{\left(K+u_{\tau}\right)}{K}\right)\\ & =-r\left(K+u\right)\frac{u_{\tau}}{K}\end{align}}

Para pequenas perturbações Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle K+u\approx K} , então:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du}{dt}=-ru_{\tau}}

Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha=-r} , é exatamente a questão discutida anteriormente (Análise de estabilidade de equações diferenciais lineares atrasadas), quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau=1} . Então há um ponto de equilíbrio estável em ${\textstyle u=0}$ se ${\textstyle -{\frac {\pi }{2}}<\alpha <0}$. Ou seja, ${\textstyle N=K}$ é um ponto de equilíbrio estável para ${\textstyle 0>r>{\frac {\pi }{2}}}$. O que significa que em ${\textstyle r={\frac {\pi }{2}}}$ o sistema perde a estabilidade, é o ponto no qual um autovalor complexo passa a ter sua parte real positiva. A bifurcação de Hopf está em ${\textstyle r={\frac {\pi }{2}}}$, exatamente neste ponto não há partes reais dos autovalores, apenas a parte imaginária do autovalor complexo e o sistema oscila em torno do ponto de equilíbrio. Para ${\textstyle r>{\frac {\pi }{2}}}$ o sistema tem uma solução estável periódica, uma vez que ainda que o sistema se afaste do ponto de equilíbrio, eventualmente ele volta a se aproximar, permanecendo assim em um comportamento periódico. A discussão foi feita com $\tau =1$, mas mas pode ser facilmente replicada para outro valores de interesse.

A solução numérica também pode ser obtida computacionalmente via Mathematica:

parametros = Rationalize[{r -> 1, k -> 1, tau -> 1}]; 
sol = NDSolve[{n'[t] == r*n[t]*(1 - n[t - tau]/k), 
      n[t /; t <= tau] == 0.5} /. parametros, n, {t, 0, 20}]; 
Plot[n[t] /. sol, {t, 0, 20}, PlotRange -> Full]

Principais materiais utilizados

1. Delay-Differential Equations (Richard Bertram, Universidade Estadual da Flórida)

Anterior: Modelo de Levins | Índice: Ecologia | Próximo: AC: Jogo da Vida