MBA: Gás simples
Anterior: Por que usar e o que são modelos baseados em indivíduos | Índice: Ecologia | Próximo: MBA: Caminhante aleatório
Colisão entre partículas
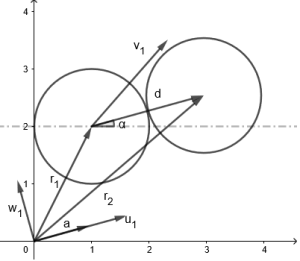
Considerando um modelo simples de gás ideal, não há força atuando sob as partículas, então a interação que ocorre entre as partículas se dá apenas por meio de colisões. Assim é necessário calcular a variação na velocidade de cada partícula após a colisão. Começando em uma dimensão, precisamos garantir a conservação do momento: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{1}v_{1}'+m_{2}v_{2}'=m_{1}v_{1}''+m_{2}v_{2}'' } E da energia cinética: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}m_{1}v_{1}'^{2}+\frac{1}{2}m_{2}v_{2}'^{2}=\frac{1}{2}m_{1}v_{1}''^{2}+\frac{1}{2}m_{2}v_{2}''^{2}} Colocando o referencial de forma que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v_2'=0} , então as velocidades no novo referencial podem ser escritas como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_i=v_i-v_2'} , de forma que da conservação do momento ficamos com: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{1}''=u_{1}'-\frac{m_{2}}{m_{1}}u_{2}'', \qquad (1) } Elevando ao quadrado: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{1}''^{2}=u_{1}'^{2}-\left(\frac{m_{2}}{m_{1}}\right)^{2}u_{2}''^{2}-2\frac{m_{2}}{m_{1}}u_{1}'u_{2}''} Substituindo na equação de conservação de energia, podemos encontrar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_2''} : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} m_{1}u_{1}'^{2}=m_{1}u_{1}''^{2}+m_{2}u_{2}''^{2}\\ m_{1}u_{1}'^{2}=m_{1}\left[u_{1}'{}^{2}+\left(\frac{m_{2}}{m_{1}}\right)^{2}u_{2}''^{2}-2\frac{m_{2}}{m_{1}}u_{1}'u_{2}''\right]+m_{2}u_{2}''^{2}\\ m_{1}u_{1}'^{2}=m_{1}u_{1}'{}^{2}+\frac{m_{2}^{2}}{m_{1}}u_{2}''^{2}-2m_{2}u_{1}'u_{2}''+m_{2}u_{2}''^{2}\\ 0=\left(\frac{m_{2}^{2}}{m_{1}}+m_{2}\right)u_{2}''^{2}+\left(-2m_{2}u_{1}'\right)u_{2}''\\ 0=\left(\frac{m_{2}+m_{1}}{m_{1}}\right)u_{2}''^{2}+\left(-2u_{1}'\right)u_{2}'' \end{array}} Calculando as raízes do segundo grau, temos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{2}''=\frac{2u_{1}'\pm\sqrt{4u_{1}'^{2}}}{2\left(\frac{m_{2}+m_{1}}{m_{1}}\right)}=\frac{m_{1}}{m_{2}+m_{1}}\left(u_{1}'\pm u_{1}'\right)} E como uma solução é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_{2}'=0} , mas queremos a situação em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_{2}'\neq0} , logo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{2}''=\frac{2m_{1}}{m_{2}+m_{1}}u_{1}'} Substituindo em (1), temos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} u_{1}''=u_{1}'-\frac{m_{2}}{m_{1}}\left(\frac{2m_{1}}{m_{2}+m_{1}}u_{1}'\right)\\ u_{1}''=\left(1-\frac{2m_{2}}{m_{2}+m_{1}}\right)u_{1}\\ u_{1}''=\left(\frac{m_{2}+m_{1}-2m_{2}}{m_{2}+m_{1}}\right)u_{1} \end{array}} Ou seja: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{1}''=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}u_{1}'} Retornando ao referencial original, sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v_i=u_i+v_2'} , temos então para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v_1'} : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} u_{1}''=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}u_{1}'\\ v_{1}''-v_{2}'=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}\left(v_{1}'-v_{2}'\right)\\ v_{1}''=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}v_{1}'+\left(1-\frac{m_{1}-m_{2}}{m_{2}+m_{1}}\right)v_{2}'\\ v_{1}''=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}v_{1}'+\frac{2m_{2}}{m_{2}+m_{1}}v_{2}' \end{array}} E de maneira análoga para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v_2'} : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} u_{2}''=\frac{2m_{1}}{m_{2}+m_{1}}u_{1}'\\ v_{2}''-v_{2}'=\frac{2m_{1}}{m_{2}+m_{1}}\left(v_{1}'-v_{2}'\right)\\ v_{2}''=\frac{2m_{1}}{m_{2}+m_{1}}v_{1}'+\left(1-\frac{2m_{1}}{m_{2}+m_{1}}\right)v_{2}'\\ v_{2}''=\frac{2m_{1}}{m_{2}+m_{1}}v_{1}'+\frac{m_{2}-m_{1}}{m_{2}+m_{1}}v_{2}' \end{array}} Um caso especial ocorre se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle m_1=m_2, \qquad (2)} então temos simplesmente: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_1''=v_2',\qquad \text{e} \qquad v_2''=v_1'} Em duas dimensões, podemos reduzir o problema a uma dimensão, considerando que toda a alteração na velocidade devido a colisão entre partículas ocorre apenas na componente paralela a reta que liga o centro das duas esferas. Considerando que a posição de cada partícula é dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{r}_{i}} , então um vetor entre as partículas pode ser escrito como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{d}=\overrightarrow{r}_{2}-\overrightarrow{r}_{1}} . Podemos projetar ambas as velocidades então fazendo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {u}_{i}'=\frac{\overrightarrow{v}_{i}\cdot\overrightarrow{d}}{\left|\overrightarrow{d}\right|}=\overrightarrow{v}_{i}\cdot\widehat{d}} Obtemos o módulo da velocidade da partícula Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i} na direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{d}} e podemos trabalhar em uma única dimensão para encontrarmos a velocidade de ambas partículas após a colisão nesta dimensão. Ao fim podemos decompor novamente a velocidade final Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_i''} em ambos os eixos mantendo a mesma direção utilizando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \theta=\arctan\left(\frac{\Delta{y}}{\Delta x}\right)} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \Delta z = z_2 - z_1} é a diferença entre a posição das partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 2} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 1} na componente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle z} .
Além disso vale lembrar que há a componente da velocidade perpendicular a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{d}} , que vamos denotar como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{w}_i=\overrightarrow{v}_i-u_{i}'\left(\cos\theta,\sin\theta\right)} . Esta componente perpendicular permanece inalterada e pode ser visualizada na figura ao lado.
Sendo assim, a velocidade final é dada por: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} \overrightarrow{v}_{i}^{\left(f\right)}=\left(u_{i}''\cos\theta,u_{i}''\sin\theta\right)+\overrightarrow{w}_{i}\\ \overrightarrow{v}_{i}^{\left(f\right)}=u_{i}''\left(\cos\theta,\sin\theta\right)+\overrightarrow{v}_{i}-u_{i}'\left(\cos\theta,\sin\theta\right)\\ \overrightarrow{v}_{i}^{\left(f\right)}=\overrightarrow{v}_{i}+\left(u_{i}''-u_{i}'\right)\left(\cos\theta,\sin\theta\right)\\ \overrightarrow{v}_{i}^{\left(f\right)}=\overrightarrow{v}_{i}^{\left(f\right)}=\overrightarrow{v}_{i}+\left(u_{i}''-u_{i}'\right)\overrightarrow{a} \end{array}} Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{a}} é um vetor unitário que nos dá a direção entre os centros das partículas. Utilizando ad identidades: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos\left(\arctan\left(x\right)\right)=\frac{1}{\sqrt{1+x^{2}}}, \qquad \sin\left(\arctan\left(x\right)\right)=\frac{x}{\sqrt{1+x^{2}}}} ficamos então com: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} \overrightarrow{a}=\left(\cos\theta,\sin\theta\right)\\ \overrightarrow{a}=\left(\cos\arctan\left(\frac{\Delta y}{\Delta x}\right),\sin\arctan\left(\frac{\Delta y}{\Delta x}\right)\right)\\ \overrightarrow{a}=\left(\frac{1}{\sqrt{1+\left(\frac{\Delta{y}}{\Delta x}\right)^{2}}},\frac{\left(\frac{\Delta y}{\Delta x}\right)}{\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^{2}}}\right)\\ \overrightarrow{a}=\frac{1}{\Delta x}\frac{1}{\sqrt{1+\left(\frac{\Delta{y}}{\Delta x}\right)^{2}}}\left(\Delta x,\Delta y\right)\\ \overrightarrow{a}=\frac{1}{\frac{\Delta x}{\Delta x}}\frac{1}{\sqrt{\Delta x^{2}+\Delta y^{2}}}\left(\Delta x,\Delta y\right) \end{array}} Logo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{a} =\frac{\left(\Delta x,\Delta y\right)}{\sqrt{\Delta x^{2}+\Delta y^{2}}}} E uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{d}=\overrightarrow{r}_{2}-\overrightarrow{r}_{1}=\left(x_{2}-x_{1},y_{2}-y_{1}\right)=\left(\Delta x,\Delta y\right)} , então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{a}= \overrightarrow{d}/\left|d\right|= \widehat{d}} . Logo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{v}_{i}^{\left(f\right)}=\overrightarrow{v}_{i}+\left(u_{i}''-u_{i}'\right)\widehat{d}} Ou ainda mais explícito, se fizermos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle m_1=m_2} , sendo as partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle j} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\neq j} , usando (2): Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{cc} \overrightarrow{v}_{i}^{\left(f\right)} & =\overrightarrow{v}_{i}+\left(u_{j}'-u_{i}'\right)\widehat{d}\\ \overrightarrow{v}_{i}^{\left(f\right)} & =\overrightarrow{v}_{i}+\left(\overrightarrow{v}_{j}\cdot\widehat{d}-\overrightarrow{v}_{i}\cdot\widehat{d}\right)\widehat{d} \end{array}} Temos então que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{v}_{i}^{\left(f\right)} =\overrightarrow{v}_{i}+\left[\left(\overrightarrow{v}_{j}-\overrightarrow{v}_{i}\right)\cdot\widehat{d}\right]\widehat{d}} Todo o cálculo exibido foi para uma partícula, para a segunda partícula, o cálculo é análogo.
Código
Anterior: Por que usar e o que são modelos baseados em indivíduos | Índice: Ecologia | Próximo: MBA: Caminhante aleatório