MBA: Caminhante aleatório

Anterior: MBA: Gás simples | Índice: Ecologia | Próximo: Contexto

Caminhante aleatório

O problema do caminhante aleatório pode ser definido da seguinte forma: Um homem começa de um ponto ${\textstyle 0}$ e caminha 1 metro em uma linha reta, então ele vira um ângulo qualquer e anda outro ${\textstyle 1}$ metro em uma linha reta. Ele repete esse processo ${\textstyle n}$ vezes, qual é a probabilidade de após estes ${\textstyle N}$ passos que o homem esteja a uma distância entre ${\textstyle r}$ e ${\textstyle r+\delta r}$ da origem.

Inspirado por este problema, propõe-se uma situação bidimensional similar. A principal diferença constitui-se no fato de que o ângulo não é mais aleatório. Reescrevendo o problema, agora em cada um dos eixos, nos quais o homem se move de maneira independe, há uma probabilidade ${\textstyle p}$ de se mover ${\textstyle 1}$ metro em um sentido e uma probabilidade ${\textstyle q=1-p}$ de se mover no sentido contrário.

Trabalhando inicialmente apenas com uma dimensão, executando ${\textstyle N}$ passos, um caminho possível para o homem terminar a simulação em uma posição ${\textstyle m=n_{1}-n_{2}}$ tendo dado ${\textstyle n_{1}}$ passos à direita e ${\textstyle n_{2}}$ passos à esquerda, é dado por:

$$p^{n_{1}}q^{n_{2}}=p^{\frac {N+m}{2}}q^{\frac {N-m}{2}}$$

Pois sendo ${\textstyle N=n_{1}+n_{2}}$ podemo escrever:

$$n_{1}={\frac {N+m}{2}},\qquad n_{2}={\frac {N-m}{2}}$$

Porém, está é a probabilidade de obtermos apenas um dos caminhos que leva o homem a ${\textstyle m}$. O número total de caminhos indistinguíveis com ${\textstyle n_{1}}$ passos à direita e ${\textstyle n_{2}}$ passos a esquerda é dado por:

$${\frac {N!}{n_{1}!n_{2}!}}={\frac {N!}{n_{1}!\left(N-n_{1}\right)!}}={\frac {N!}{\left({\frac {N+m}{2}}\right)!\left({\frac {N-m}{2}}\right)!}}$$

Temos então que a probabilidade estar na posição ${\textstyle m}$ após ${\textstyle N}$ passos é dado por:

$$p\left(m,N\right)={\frac {N!}{\left({\frac {N+m}{2}}\right)!\left({\frac {N-m}{2}}\right)!}}p^{\frac {N+m}{2}}q^{\frac {N-m}{2}}$$

Ou reescrevendo ${\textstyle n_{1}=n}$ para facilitar, e lembrando que ${\textstyle n_{1}={\frac {N+m}{2}}}$ e ${\textstyle N=n_{1}+n_{2}}$:

$$p\left(n\right)={\frac {N!}{n!\left(N-n\right)!}}p^{n}q^{N-n}=\left({\begin{array}{c}N\\n\end{array}}\right)p^{n}q^{N-n}$$

Onde ${\textstyle \left({\begin{array}{c}N\\n\end{array}}\right)=C_{n}^{N}}$ também é chamado de combinatória. Utilizando o binômio de Newton:

$$\left(x+y\right)^{n}=\sum _{k=0}^{n}\left({\begin{array}{c}n\\k\end{array}}\right)x^{n-k}y^{k}$$

Temos a normalização:

$$\sum _{n=0}^{n}p\left(n\right)=\sum _{n=0}^{n}\left({\begin{array}{c}N\\n\end{array}}\right)q^{N-n}p^{n}=\left(p+q\right)^{N}=1$$

Uma vez que ${\textstyle p+q=1}$. E lembrando que ${\textstyle p\left(n\right)}$ é a probabilidade de estar em ${\textstyle m=2n-N}$, ou seja de obtermos ${\textstyle n}$ vezes passo a direita em ${\textstyle N}$ passos no total, então o valor médio de ${\textstyle n}$ pode ser dado por:

$$\left\langle n\right\rangle =\sum _{n=0}^{N}np\left(n\right)$$

Derivando o binômio de Newton:

$${\begin{array}{c}p{\frac {d}{dp}}\left(p+q\right)^{N}=pN\left(p+q\right)^{N-1}=pN\end{array}}$$

E também:

$${\begin{aligned}p{\frac {d}{dp}}\left(p+q\right)^{N}&=p{\frac {d}{dp}}\left[\sum _{n=0}^{n}\left({\begin{array}{c}N\\n\end{array}}\right)q^{N-n}p^{n}\right]\\&=p\sum _{n=0}^{n}n\left({\begin{array}{c}N\\n\end{array}}\right)q^{N-n}p^{n-1}\\&=\sum _{n=0}^{n}n\left({\begin{array}{c}N\\n\end{array}}\right)q^{N-n}p^{n}\\&=\sum _{n=0}^{n}np\left(n\right)\end{aligned}}$$

Então:

$$pN=\sum _{n=0}^{n}np\left(n\right)=\left\langle n\right\rangle$$

E com isso podemos obter a posição final média ${\textstyle \left\langle m\right\rangle }$. Utilizando a notação anterior posição final exata é ${\textstyle m=n_{1}-n_{2}}$, ou ainda podemos rescrever como ${\textstyle m=2n-N}$, pois:

$$n_{1}-n_{2}=n_{1}-\left(N-n_{1}\right)=2n_{1}-N$$

A partir destes resultados podemos obter:

$${\begin{aligned}\left\langle m\right\rangle &=\sum _{n=0}^{N}mp\left(n\right)\\&=\sum _{n=0}^{N}\left(2n-N\right)p\left(n\right)\\&=2\sum _{n=0}^{N}np\left(n\right)-\sum _{n=0}^{N}Np\left(n\right)\\&=2\left\langle n\right\rangle -N\sum _{n=0}^{N}p\left(n\right)\\&=2\left\langle n\right\rangle -N\end{aligned}}$$

A princípio, não temos motivos para dar preferência para o movimento em nenhuma direção, logo é razoável utilizar ${\textstyle p=q=1/2}$, o que resulta em ${\textstyle \left\langle n\right\rangle =N/2}$ consequentemente ${\textstyle \left\langle m\right\rangle =0}$. O que pode parecer contra-intuitivo para nosso modelo, mas além de distribuirmos animais por todo o espaço, o que resultado implica é a posição final média, mas é preciso entender que não impede que ao longo da simulação cada indivíduo percorra diferentes áreas do espaço.

Distribuição Gaussiana

Quando ${\textstyle N\rightarrow \infty }$ tendo ${\textstyle p\not \approx 1}$ temos a distribuição Gaussiana:

$$p\left(n\right)=\left({\begin{array}{c}N\\n\end{array}}\right)p^{n}q^{N-n}\approx {\frac {1}{\sqrt {2\pi Npq}}}\exp \left({\frac {-\left(n-Np\right)^{2}}{2Npq}}\right)$$

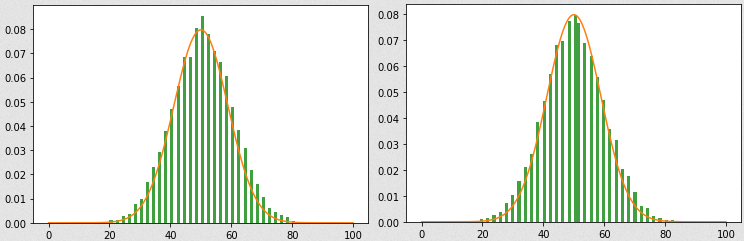
Foi realizada uma simulação utilizando Python e o módulo Mesa, grande parte do código segue a mesma discussão feita anteriormente no Jogo da Vida. A figura ilustra uma simulação com 10.000 caminhantes aleatórios em uma grade 100 X 100, iniciando na posição P=(50,50).

Resultado da simulação com a distribuição gaussiana sobreposta para N=100 para ambas as coordenadas.

Código

#Bibliotecas necessárias
from mesa import Agent, Model                                      #Classes Agente e Modelo
from mesa.time import SimultaneousActivation                       #Agendador simultâneo
from mesa.space import MultiGrid                                   #Malha multigrid
import random                                                      #Número aleatórios

#AGENTE---------------------------------------------------------------------------------
class Agente(Agent):
    """Classe do agente"""
    def __init__(self,modelo):
      """Bibliotecas necessárias"""
      #modelo     - Modelo que ao qual o agente pertence
      super().__init__(self,modelo)             #Necessário para funcionar o modelo
      self.ppos=(0,0)
      
    def step(self):
      """Método obrigatório que prepara as mudanças"""
      dx = (+1) if (random.random()<0.5) else(-1)
      dy = (+1) if (random.random()<0.5) else (-1)
      self.ppos = (self.pos[0]+dx,self.pos[1]+dy)                                 #Próxima posição
          
    def advance(self):
        """Método obrigatório que aplica as mudanças"""
        self.model.grid.move_agent(self, self.ppos)

#MODELO
class Modelo(Model):
    """Modelo geral"""

    def __init__(self, modelo,N,seed=None):
        """Função chamada quando o modelo é inicializazdo"""
        # Modelo   - Dicionário com especificações do modelo
        # N        - Quantiade de caminhantes
        # seed     - Seed dos números aleatórios do modelo do mesa
        
        largura = modelo["Largura"];altura=modelo["Altura"];seed_random=modelo["Seed"]
        random.seed(seed_random)                                 #Seed dos números aleatórios
        self.grid     = MultiGrid(largura, altura, True)         #Configura a grade
        self.schedule = SimultaneousActivation(self)             #Configura o agendador
        self.running  = True                                     #Condiçao para seguir executando o modelo
        for n in range(N):
          a = Agente(self)
          self.schedule.add(a)
          X= 50
          Y= 50
          self.grid.place_agent(a, (X, Y))
            
    def step(self):
        """Avançar um passo do modelo"""
        self.schedule.step()                              #Avançamos os agentes


MAX =100
N=10000
modelo  = {"Largura":100   ,"Altura":100       ,"Seed":0} 
M = Modelo(modelo,N)
for i in range(MAX):
    M.step()
    if ((i+1)%(MAX/100)==0):
      print(str(100*(1+i)/MAX)+"%")

E o gráfico foi gerado utilizando:

import numpy as np
import matplotlib.pyplot as plt


x=[];y=[]
for a in M.schedule.agents:
  x.append(a.pos[0])
  y.append(a.pos[1])

a,b,c=plt.hist(x, 70, density=True, facecolor='g', alpha=0.75)
m=1
K=100
X=np.arange(0,100, 0.1)
sigma = 2*np.pi*K*0.5*0.5
plt.plot(X,np.exp(-((X-K*0.5)**2)/sigma)/(np.sqrt(sigma)))

Acima fazendos um histograma das posições em x, uma alteração simples permite visualizarmos o equivalente em y.

Principais materiais utilizados:

• The Problem of the Random Walk. (Karl Pearson, Nature)
• A Modern Course in Statistical Physics (L.E. Reichl)

Anterior: MBA: Gás simples | Índice: Ecologia | Próximo: Contexto