Método dos Elementos Finitos - Equação do Calor

Equação do Calor (1D)

A equação do calor em 1D descreve a evolução da temperatura $u(x,t)$ ao longo do tempo em uma barra unidimensional, sujeita a condições de contorno e a uma difusão térmica (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} ). A equação diferencial que governa o comportamento do sistema é dada por:

Forma Forte

${\frac {\partial u(x,t)}{\partial t}}=\alpha {\frac {\partial ^{2}u(x,t)}{\partial x^{2}}}$

Condição Inicial

$u(t=0,x)=sin(\pi x)$

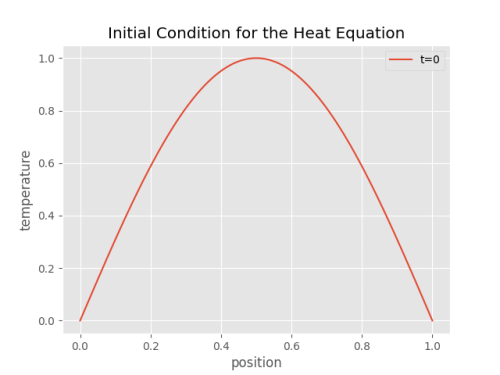
Figura 1: Condição inicial para a equação do calor.

Condição de Contorno

$u(t,x=0)=0=u(t,x=L)$

Método dos Elementos Finitos (FEM)

O Método dos Elementos Finitos (FEM, do inglês Finite Element Method) é uma técnica amplamente utilizada para resolver equações diferenciais parciais, como a equação do calor. Para aplicar o FEM à equação do calor em 1D, a barra [0,1] é dividida em um número finito de elementos (intervalos) de comprimento $\Delta x$, e as variáveis contínuas são aproximadas por funções de base definidas localmente em cada elemento.

Forma Fraca

Apesar de o problema estar completo na forma forte, que é a mostrada acima, precisamos representá-lo na forma equivalente, chamada forma fraca. A forma fraca é preferível por diversos motivos, sendo um dos principais o fato de que ela não possui derivadas de segunda ordem, possibilitando o uso de funções lineares para fazer a aproximação, que na forma forte teriam essa derivada nula. Para obter a forma fraca a partir da forma forte, deve-se seguir os seguintes passos:

• Multiplica-se por uma função teste $v$ do mesmo espaço de funções definido nos elementos.

${\frac {\partial u(x,t)}{\partial t}}v=\alpha {\frac {\partial ^{2}u(x,t)}{\partial x^{2}}}v$

$\int _{0}^{L}{\frac {\partial u(x,t)}{\partial t}}v(x)\,dx=\alpha \int _{0}^{L}{\frac {\partial ^{2}u(x,t)}{\partial x^{2}}}v(x)\,dx$

$\int _{0}^{1}{\frac {\partial ^{2}u}{\partial x^{2}}}v\,dx=\left[{\frac {\partial u}{\partial x}}v\right]_{0}^{1}-\int _{0}^{1}{\frac {\partial u}{\partial x}}{\frac {\partial v}{\partial x}}\,dx$

$\int _{0}^{1}{\frac {\partial u}{\partial t}}v\,dx+\int _{0}^{1}\alpha {\frac {\partial u}{\partial x}}{\frac {\partial v}{\partial x}}\,dx=\left[\alpha {\frac {\partial u}{\partial x}}v\right]_{0}^{1}$

O lado direito zera devido às condições de contorno

$\int _{0}^{1}{\frac {\partial u}{\partial t}}v\,dx+\int _{0}^{1}\alpha {\frac {\partial u}{\partial x}}{\frac {\partial v}{\partial x}}\,dx=0$

Essa é a forma fraca, mas ainda precisamos discretizá-la tanto no espaço quanto no tempo para aplicar o FEM.

Fenics

O Fenics é uma plataforma de computação popular e de código aberto para resolver equações diferenciais parciais (PDEs) usando o método dos elementos finitos (FEM). Na prática, ajuda a discretizar a parte espacial e a resolver o sistema de equações lineares.

Discretização Temporal

Devemos discretizar a parte temporal para obter a forma fraca final para usar o Fenics. Para isso, usaremos o método de Euler Implícito.

Fazemos a aproximação:

${\frac {\partial u}{\partial t}}\approx {\frac {u^{t+1}-u^{t}}{\Delta t}}$

Substituindo na forma fraca: $\int _{0}^{L}{\frac {u^{t+1}-u^{t}}{\Delta t}}v\,dx+\int _{0}^{L}\alpha {\frac {\partial u^{t+1}}{\partial x}}{\frac {\partial v}{\partial x}}\,dx=0$

Multiplicando por $\Delta t$: $\int _{0}^{L}u^{t+1}v\,dx-\int _{0}^{L}u^{t}v\,dx+\Delta t\int _{0}^{L}\alpha {\frac {\partial u^{t+1}}{\partial x}}{\frac {\partial v}{\partial x}}\,dx=0$

Reorganizando os termos, temos: $\int _{0}^{L}u^{t+1}v\,dx+\Delta t\int _{0}^{L}\alpha {\frac {\partial u^{t+1}}{\partial x}}{\frac {\partial v}{\partial x}}\,dx=\int _{0}^{L}u^{t}v\,dx$

Para fazer a implementação no Fenics, devemos escrever na versão mais geral, com dimensão arbitrária, utilizando gradiente e produto escalar:

$\int _{\Omega }u^{t+1}v\,d\Omega +\Delta t\int _{\Omega }\alpha \nabla u^{t+1}\cdot \nabla v\,d\Omega =\int _{\Omega }u^{t}v\,d\Omega$

Resultados

Como esperado pela solução analítica, a partir das condições iniciais e de contorno escolhidas, a amplitude do seno diminui exponencialmente com o tempo

Figura 2: Evolução temporal para a equação do calor utilizando o método dos elementos finitos, com dt=0.001.

O intervalo de tempo escolhido tem grande influência na acurácia do resultado. Nas figuras 3, 4 e 5 são mostradas a solução obtida pelo FEM em comparação com a solução analítica para diferentes instantes de tempo. É possível perceber que a solução, independente do intervalo de tempo (dt) escolhido, é muito boa para tempos curtos. Entretanto, quanto maior o tempo, maior será o erro para dt maiores.

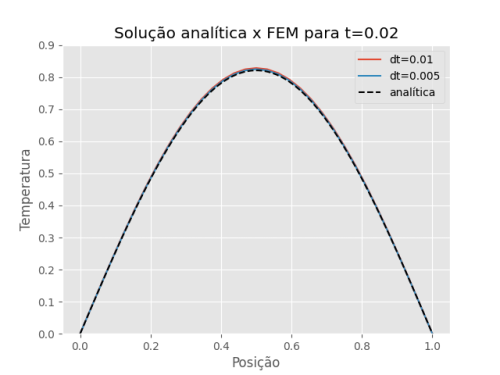
Figura 2: Comparação da solução analítica com a solução do método dos elementos finitos para diferentes intervalos de tempo e mantendo fixo t=0.02.

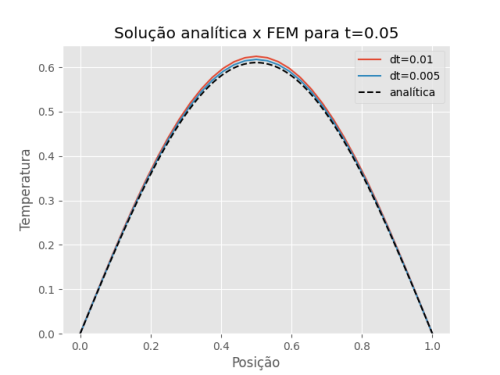
Figura 3: Comparação da solução analítica com a solução do método dos elementos finitos para diferentes intervalos de tempo e mantendo fixo t=0.05.

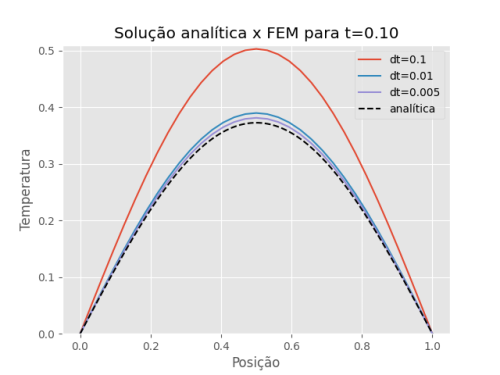
Figura 4: Comparação da solução analítica com a solução do método dos elementos finitos para diferentes intervalos de tempo e mantendo fixo t=0.01..

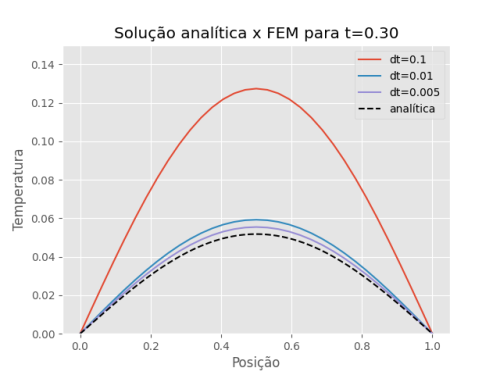
Figura 5: Comparação da solução analítica com a solução do método dos elementos finitos para diferentes intervalos de tempo e mantendo fixo t=0.3.

Alem disso, para demonstrar a influência do número de elementos para a qualidade do resultado, são comparadas nas figuras 6, 7 e 8 a solução analítica com a solução obtida pelo FEM. Para um número de elementos muito pequeno, a curva é uma aproximação grosseira e claramente linear em partes. Quando aumentamos os elementos, entretanto, rapidamente a curva suaviza e obtemos uma ótima aproximação para o resultado analítico. Assim como discutido anteriormente, a aproximação piora com o passar do tempo.

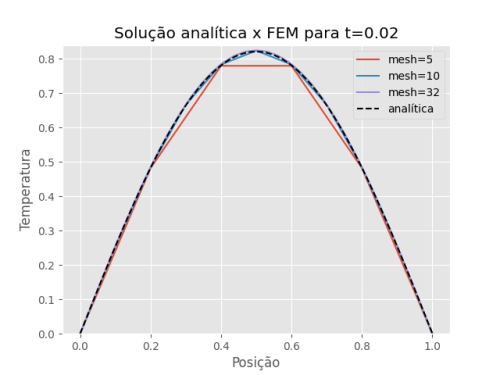
Figura 6: Comparação de diferentes números de elementos (mesh) com a solução analítica, mantendo fixos dt=0.0001 e mantendo fixo t=0.02.

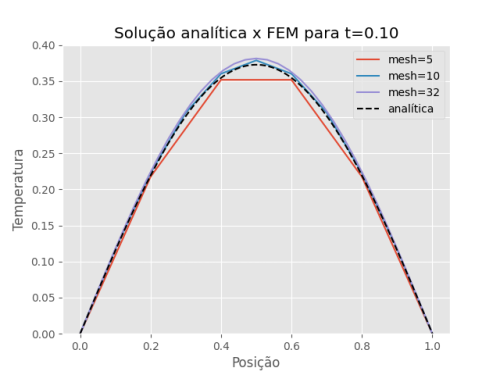
Figura 7: Comparação de diferentes números de elementos (mesh) com a solução analítica, mantendo fixos dt=0.0001 e mantendo fixo t=0.1.

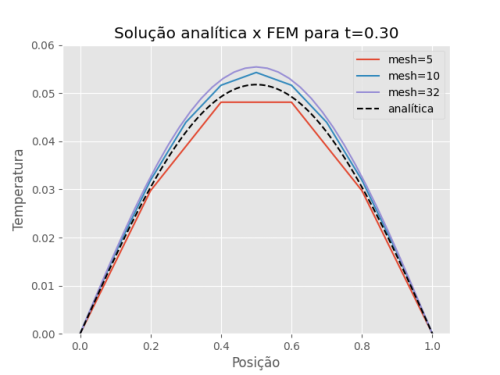
Figura 8: Comparação de diferentes números de elementos (mesh) com a solução analítica, mantendo fixos dt=0.0001 e mantendo fixo t=0.3.