MBA: Caminhante aleatório: mudanças entre as edições
(Criou página com '{{Ecologia| Por que usar e o que são modelos baseados em indivíduos |Contexto}} = Caminhante aleatório = O problema do caminhante aleatório pode ser definido da se...') |
Sem resumo de edição |
||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[ | {{Ecologia| [[MBA: Gás simples]] |[[Contexto]]}} | ||
= Caminhante aleatório = | = Caminhante aleatório = | ||
O problema do caminhante aleatório pode ser definido da seguinte forma: Um homem começa de um ponto <math display="inline">0</math> e caminha 1 metro em uma linha reta, então ele vira um ângulo qualquer e anda outro <math display="inline">1</math> metro em uma linha reta. Ele repete esse processo <math display="inline">n</math> vezes, qual é a probabilidade de após estes <math display="inline">N</math> passos que o homem esteja a uma distância entre <math display="inline">r</math> e <math display="inline">r+\delta r</math> da origem. | O problema do caminhante aleatório pode ser definido da seguinte forma: Um homem começa de um ponto <math display="inline">0</math> e caminha 1 metro em uma linha reta, então ele vira um ângulo qualquer e anda outro <math display="inline">1</math> metro em uma linha reta. Ele repete esse processo <math display="inline">n</math> vezes, qual é a probabilidade de após estes <math display="inline">N</math> passos que o homem esteja a uma distância entre <math display="inline">r</math> e <math display="inline">r+\delta r</math> da origem. | ||
| Linha 145: | Linha 145: | ||
* [https://books.google.com.br/books?id=ue1ScAAACAAJ A Modern Course in Statistical Physics] (L.E. Reichl) | * [https://books.google.com.br/books?id=ue1ScAAACAAJ A Modern Course in Statistical Physics] (L.E. Reichl) | ||
{{Ecologia| [[ | {{Ecologia| [[MBA: Gás simples]] |[[Contexto]]}} | ||
Edição atual tal como às 03h14min de 21 de julho de 2022
Anterior: MBA: Gás simples | Índice: Ecologia | Próximo: Contexto
Caminhante aleatório
O problema do caminhante aleatório pode ser definido da seguinte forma: Um homem começa de um ponto e caminha 1 metro em uma linha reta, então ele vira um ângulo qualquer e anda outro metro em uma linha reta. Ele repete esse processo vezes, qual é a probabilidade de após estes passos que o homem esteja a uma distância entre e da origem.
Inspirado por este problema, propõe-se uma situação bidimensional similar. A principal diferença constitui-se no fato de que o ângulo não é mais aleatório. Reescrevendo o problema, agora em cada um dos eixos, nos quais o homem se move de maneira independe, há uma probabilidade de se mover metro em um sentido e uma probabilidade de se mover no sentido contrário.
Trabalhando inicialmente apenas com uma dimensão, executando passos, um caminho possível para o homem terminar a simulação em uma posição tendo dado passos à direita e passos à esquerda, é dado por:
Distribuição Gaussiana
Quando tendo temos a distribuição Gaussiana:
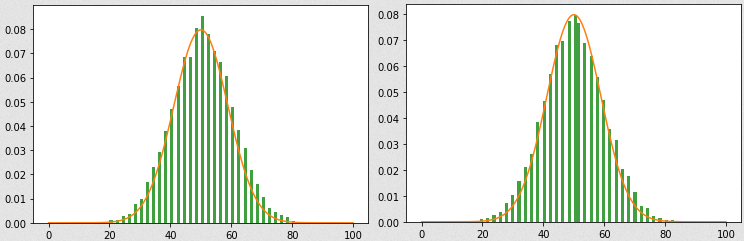
Foi realizada uma simulação utilizando Python e o módulo Mesa, grande parte do código segue a mesma discussão feita anteriormente no Jogo da Vida. A figura ilustra uma simulação com 10.000 caminhantes aleatórios em uma grade 100 X 100, iniciando na posição P=(50,50).
Código
#Bibliotecas necessárias
from mesa import Agent, Model #Classes Agente e Modelo
from mesa.time import SimultaneousActivation #Agendador simultâneo
from mesa.space import MultiGrid #Malha multigrid
import random #Número aleatórios
#AGENTE---------------------------------------------------------------------------------
class Agente(Agent):
"""Classe do agente"""
def __init__(self,modelo):
"""Bibliotecas necessárias"""
#modelo - Modelo que ao qual o agente pertence
super().__init__(self,modelo) #Necessário para funcionar o modelo
self.ppos=(0,0)
def step(self):
"""Método obrigatório que prepara as mudanças"""
dx = (+1) if (random.random()<0.5) else(-1)
dy = (+1) if (random.random()<0.5) else (-1)
self.ppos = (self.pos[0]+dx,self.pos[1]+dy) #Próxima posição
def advance(self):
"""Método obrigatório que aplica as mudanças"""
self.model.grid.move_agent(self, self.ppos)
#MODELO
class Modelo(Model):
"""Modelo geral"""
def __init__(self, modelo,N,seed=None):
"""Função chamada quando o modelo é inicializazdo"""
# Modelo - Dicionário com especificações do modelo
# N - Quantiade de caminhantes
# seed - Seed dos números aleatórios do modelo do mesa
largura = modelo["Largura"];altura=modelo["Altura"];seed_random=modelo["Seed"]
random.seed(seed_random) #Seed dos números aleatórios
self.grid = MultiGrid(largura, altura, True) #Configura a grade
self.schedule = SimultaneousActivation(self) #Configura o agendador
self.running = True #Condiçao para seguir executando o modelo
for n in range(N):
a = Agente(self)
self.schedule.add(a)
X= 50
Y= 50
self.grid.place_agent(a, (X, Y))
def step(self):
"""Avançar um passo do modelo"""
self.schedule.step() #Avançamos os agentes
MAX =100
N=10000
modelo = {"Largura":100 ,"Altura":100 ,"Seed":0}
M = Modelo(modelo,N)
for i in range(MAX):
M.step()
if ((i+1)%(MAX/100)==0):
print(str(100*(1+i)/MAX)+"%")
E o gráfico foi gerado utilizando:
import numpy as np import matplotlib.pyplot as plt x=[];y=[] for a in M.schedule.agents: x.append(a.pos[0]) y.append(a.pos[1]) a,b,c=plt.hist(x, 70, density=True, facecolor='g', alpha=0.75) m=1 K=100 X=np.arange(0,100, 0.1) sigma = 2*np.pi*K*0.5*0.5 plt.plot(X,np.exp(-((X-K*0.5)**2)/sigma)/(np.sqrt(sigma)))
Acima fazendos um histograma das posições em x, uma alteração simples permite visualizarmos o equivalente em y.
Principais materiais utilizados:
- The Problem of the Random Walk. (Karl Pearson, Nature)
- A Modern Course in Statistical Physics (L.E. Reichl)
Anterior: MBA: Gás simples | Índice: Ecologia | Próximo: Contexto




























![{\displaystyle {\begin{aligned}p{\frac {d}{dp}}\left(p+q\right)^{N}&=p{\frac {d}{dp}}\left[\sum _{n=0}^{n}\left({\begin{array}{c}N\\n\end{array}}\right)q^{N-n}p^{n}\right]\\&=p\sum _{n=0}^{n}n\left({\begin{array}{c}N\\n\end{array}}\right)q^{N-n}p^{n-1}\\&=\sum _{n=0}^{n}n\left({\begin{array}{c}N\\n\end{array}}\right)q^{N-n}p^{n}\\&=\sum _{n=0}^{n}np\left(n\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbf733c2f884cb90365fb9ae7e30eb3763bf2e6d)