Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou

Grupo: Paula Pandolfo, Ramiro de Souza, Samuel Dieterich e Wallace Carvalho

Objetivo: Este trabalho tem dois objetivos principais: apresentar alguns resultados analíticos de osciladores lineares acoplados, comparando esses resultados com simulações computacionais; e implementar o modelo de osciladores acoplados com a adição de um termo quadrático, conforme inicialmente apresentado pelo artigo original do problema de Fermi-Pasta-Ulam-Tsingou (FPUT), analisando os resultados. Apresentaremos algumas simulações dos casos bidimensionais, mas as análises de resultados serão restritas aos casos unidimensionais, por simplicidade.

Introdução

Os osciladores talvez sejam os sistemas mais estudados em toda a Física, sendo capazes de modelar uma ampla gama de fenômenos, como, p. ex., pêndulos, circuitos eletrônicos e interações moleculares. O comportamento linear desse tipo de sistema, em particular, possui resultados analíticos bem conhecidos, facilitando o tratamento matemático de sistemas complexos que possam ser modelados por conjuntos de osciladores.

O problema de FPUT (Enrico Fermi, John R. Pasta, Stanislaw M. Ulam, Mary Tsingou) resulta da análise computacional de um sistema de partículas que apenas interagem com seus vizinhos, com interações modeladas por oscilações acopladas com a adição de um termo não-linear, que pode ser quadrático ou cúbico. O intuito original da simulação era estudar como tal sistema evolui para o equilíbrio térmico. Se as forças envolvidas forem estritamente lineares, a energia alocada em cada modo de vibração não se distribui entre os demais modos, e o sistema nunca atinge o equilíbrio térmico. Adicionando termos não lineares, supunha-se que, pelo Teorema da Equipartição da Energia, a energia total do sistema seria distribuída uniformemente entre os modos normais de vibração após um certo tempo, resultando no equilíbrio térmico do sistema. Entretanto, isso não foi observado nas simulações computacionais.

O caso foi estudado pela primeira vez em Los Alamos, nos Estados Unidos, e implementado no computador MANIAC I (Mathematical Analyzer Numerical Integrator and Automatic Computer Model I). Além dos três participantes coautores do artigo , que relataram o caso em 1955, Mary Tsingou implementou o código e resolveu numericamente o sistema. Atualmente, por essa razão, o paradoxo é denominado pela sigla FPUT (Fermi-Pasta-Ulam-Tsingou).

A abordagem adotada no presente trabalho é a seguinte: inicialmente, serão apresentados alguns resultados teóricos bem conhecidos de osciladores lineares acoplados. Em seguida, compararemos esses resultados com simulações computacionais, a fim de exemplificar visualmente seu significado. Após apresentar as fundações teóricas desses casos mais simples em que as forças são lineares, trataremos do problema de FPUT em si, examinando a situação em que a interação não-linear se dá através de um termo quadrático nas coordenadas generalizadas utilizadas. Tal tratamento tem de ser majoritariamente computacional, já que as equações diferenciais envolvidas não são, em geral, fáceis de se resolver. [falta complementar]

Osciladores Lineares Acoplados

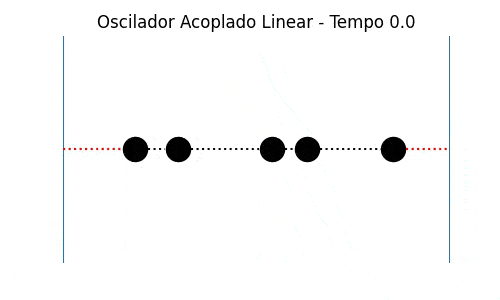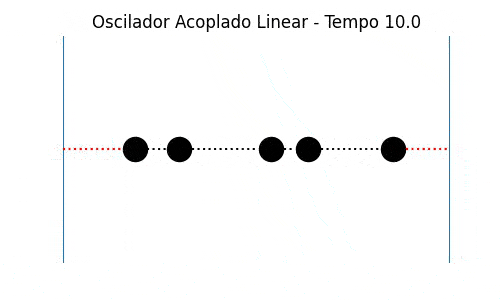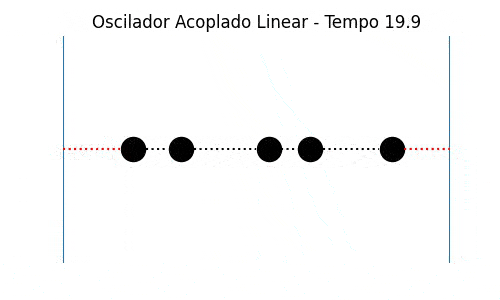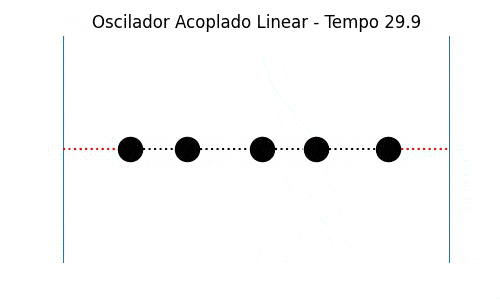
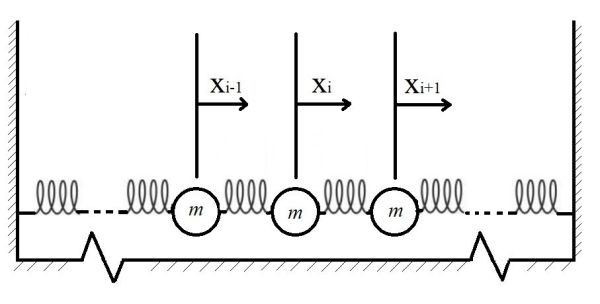
Um modelo geral de sistema unidimensional de osciladores lineares acoplados é ilustrado pela Figura 1.

Figura 1. Ilustração de um modelo geral unidimensional de oscilações acopladas. A figura foi criada por Paula Pandolfo, uma das integrantes do grupo.

Cada partícula possui duas vizinhas com as quais interage por meio das molas, exceto as partículas localizadas nos extremos da cadeia, que possuem apenas uma partícula vizinha cada. As interações das partículas dos extremos das cadeias se restringem, portanto, à interação com uma vizinha e com uma mola conectada a uma das paredes externas à cadeia. Como este problema é unidimensional, a posição de cada partícula pode ser descrita por apenas um grau de liberdade. Vamos escolher os deslocamentos $x_{i}$ em relação à respectiva posição de equilíbrio da partícula $i$ como nossas coordenadas generalizadas, definindo como positivos os deslocamentos para a direita e negativos para a esquerda. No total, um sistema com $N$ partículas terá, portanto, $N$ graus de liberdade. Vamos tratar aqui o caso em que as forças das molas são lineares, seguindo a lei de Hooke; i.e., forças dadas pela forma $F=-kx$. Além disso, para simplificar e minimizar o número de parâmetros das simulações, vamos considerar que, em todos os casos mostrados, todas as molas possuem as mesmas constantes de acoplamento linear $k$ e todas as partículas possuem as mesmas massas $m$.

N=2

Nota: O conteúdo abaixo segue aproximadamente a seção 12.2 de Marion e Thornton (2004). Entretanto, há diversas modificações e inclusões. Por exemplo, na descrição das equações de movimento e nas definições dos modos normais.

Para nos familiarizarmos com este sistema, consideremos inicialmente o caso do oscilador linear acoplado mais simples, com apenas duas partículas ($N=2$), cada uma com massa $m$, e três molas com os mesmos valores de constantes, $k$.

Utilizando a segunda lei de Newton, mostra-se que as equações de movimento do sistema são:

${\begin{aligned}m{\ddot {x}}_{1}&=-kx_{1}-k(x_{1}-x_{2})\\m{\ddot {x}}_{2}&=-kx_{2}-k(x_{2}-x_{1}){\text{.}}\quad (1)\\\end{aligned}}$

Uma forma direta de se montar as equações de movimento de um sistema acoplado é pensar em termos dos deslocamentos em relação às posições de equilíbrio ($x_{i}$, com $i=1,2$, no sistema considerado aqui). Por exemplo, na primeira das equações acima, a partícula 1 está sujeita à força elástica da mola conectada à parede (termo $-kx_{1}$) e à força da mola conectada à partícula 2 (termo $-k(x_{1}-x_{2})$). Esse último termo é definido conforme o seguinte: caso a mola que está conectada às partículas 1 e 2 esteja comprimida, $x_{1}$ deve ser maior que $x_{2}$ e a partícula 1 estará sofrendo uma força que é contrária à compressão, ou seja, com sinal negativo. De modo semelhante para a partícula 2, mas nesse caso, devido à posição ocupada pela partícula 2 na cadeia, com $x_{1}$ maior que $x_{2}$, o sentido da força contrária à compressão tem sinal positivo, manifestando a terceira lei de Newton.

Uma dificuldade imposta pelo sistema (1) é o fato das equações serem acopladas, que a aceleração da partícula 1 depende da posição da partícula 2, e vice-versa. Vamos supor que esse sistema de equações tenha soluções na seguinte forma:

${\begin{aligned}x_{1}(t)&=A_{1}e^{-i\omega t}\\x_{2}(t)&=A_{2}e^{-i\omega t}{\text{,}}\quad (2)\end{aligned}}$

onde $A_{1}$ e $A_{2}$ são constantes e $\omega$ é uma frequência angular ainda indeterminada. Essa suposição é fisicamente justificável: sabemos que as soluções são oscilatórias, e exponenciais imaginárias podem ser escritas em termos de senos e cossenos pela fórmula de Euler. Se substituirmos as expressões em (2) na equação (1) e rearranjarmos os termos, obteremos:

${\begin{aligned}-mw^{2}A_{1}e^{-i\omega t}+2kA_{1}e^{-i\omega t}-kA_{2}e^{-i\omega t}&=0\\-mw^{2}A_{2}e^{-i\omega t}+2kA_{2}e^{-i\omega t}-kA_{1}e^{-i\omega t}&=0{\text{.}}\\\end{aligned}}$

Ou, eliminando as exponenciais e reagrupando termos:

${\begin{aligned}(2k-mw^{2})&A_{1}&-kA_{2}&=0\\-k&A_{1}&+(2k-mw^{2})A_{2}&=0{\text{.}}\quad (3)\\\end{aligned}}$

O sistema de equações (3) apenas terá soluções não triviais se o determinante da matriz dos coeficientes que acompanham os $A_{i}$ for igual a zero, i.e.:

${\begin{vmatrix}(2k-mw^{2})&-k\\-k&(2k-mw^{2})\end{vmatrix}}=0{\text{.}}$

O resultado desse determinante ser igual a zero é uma equação quadrática simples em $\omega ^{2}$, sendo as soluções facilmente obtidas. Como para cada solução $\omega$ existe uma solução $-\omega$, apresentaremos apenas o módulo das frequências:

${\begin{aligned}\omega _{1}={\sqrt {\frac {k}{m}}}\quad {\text{,}}\quad \omega _{2}={\sqrt {\frac {3k}{m}}}{\text{.}}\quad (4)\end{aligned}}$

$\omega _{1}$ e $\omega _{2}$ são então denominadas as frequências características ou autofrequências do sistema. As soluções mais gerais do sistema de equações diferenciais lineares (1) vão ser então combinações lineares das soluções (2) com as frequências dadas por (4):

${\begin{aligned}x_{1}(t)=a_{1}^{1}e^{i\omega _{1}t}&+a_{1}^{2}e^{-i\omega _{1}t}&+a_{1}^{3}e^{i\omega _{2}t}&+a_{1}^{4}e^{-i\omega _{2}t}\\x_{2}(t)=a_{2}^{1}e^{i\omega _{1}t}&+a_{2}^{2}e^{-i\omega _{1}t}&+a_{2}^{3}e^{i\omega _{2}t}&+a_{2}^{4}e^{-i\omega _{2}t}{\text{.}}\quad (5)\end{aligned}}$

Nota-se que cada uma das soluções é uma superposição (em geral) complicada que envolve as duas autofrequências. Isso é uma consequência direta do acoplamento presente no sistema (1). Para eliminar este acoplamento, vamos definir novas variáveis: $\eta _{1}=x_{1}+x_{2}$ e $\eta _{2}=x_{1}-x_{2}$, ou

$x_{1}={\frac {\eta _{1}+\eta _{2}}{2}}\quad {\text{,}}\quad x_{2}={\frac {\eta _{1}-\eta _{2}}{2}}{\text{.}}$

Substituindo essas expressões no sistema de equações (1), ficamos com:

${\begin{aligned}&m({\ddot {\eta }}_{1}+{\ddot {\eta }}_{2})+k\eta _{1}+3k\eta _{2}=0\\&m({\ddot {\eta }}_{1}-{\ddot {\eta }}_{2})+k\eta _{1}-3k\eta _{2}=0{\text{.}}\end{aligned}}$

Se somarmos as duas equações acima, e se subtrairmos a segunda da primeira, obtemos, respectivamente:

${\begin{aligned}&m{\ddot {\eta }}_{1}+k\eta _{1}=0\\&m{\ddot {\eta }}_{2}+3k\eta _{2}=0{\text{.}}\end{aligned}}$

Reconhecemos imediatamente as equações acima como equações de osciladores harmônicos simples, desacopladas e, portanto, com soluções independentes. As soluções são dadas por

${\begin{aligned}\eta _{1}(t)&=c_{1}e^{i\omega _{1}t}+c_{2}e^{-i\omega _{1}t}\\\eta _{2}(t)&=c_{3}e^{i\omega _{2}t}+c_{4}e^{-i\omega _{2}t}\quad (6)\end{aligned}}$

$\eta _{1}$ e $\eta _{2}$ são chamadas de coordenadas normais. Por definição, são coordenadas que desacoplam as equações diferenciais do sistema e possuem soluções com frequências únicas, bem definidas. Sempre podem ser escritas como algum tipo de combinação linear das coordenadas originais. De modo semelhante, as coordenadas usuais do sistema sempre podem ser escritas como combinações lineares das coordenadas normais. No caso geral, para mais partículas, a combinação linear dos deslocamentos $x_{i}$ que produz as coordenadas normais é trabalhosa de se encontrar. Note-se que, no caso de duas partículas, é simples encontrá-las meramente por inspeção. Se impusermos as condições iniciais $x_{1}(0)=x_{2}(0)$ e ${\dot {x}}_{1}(0)={\dot {x}}_{2}(0)$, $\eta _{2}(0)=x_{1}(0)-x_{2}(0)=0$ e as constantes $c_{3}$ e $c_{4}$ vão ser iguais a zero, o que implica $\eta _{2}(t)=0$, para todo $t$. Esse primeiro modo normal corresponderá a uma oscilação simétrica, em que as duas partículas oscilarão em fase, com frequência $\omega _{1}$. De modo semelhante, se impusermos as condições iniciais $x_{1}(0)=-x_{2}(0)$ e ${\dot {x}}_{1}(0)=-{\dot {x}}_{2}(0)$, $\eta _{1}(t)=0$, para todo $t$, e as partículas oscilarão fora de fase, com frequência $\omega _{2}$. Pelas expressões dadas em (4) e pelas simulações abaixo, destaca-se que a frequência associada ao modo simétrico é menor do que a frequência do modo antissimétrico. Esse é um resultado geral de oscilações acopladas: quanto maior o grau de simetria da oscilação, menor o valor da frequência.

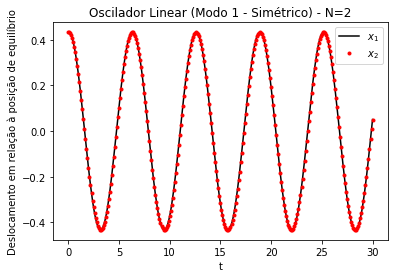
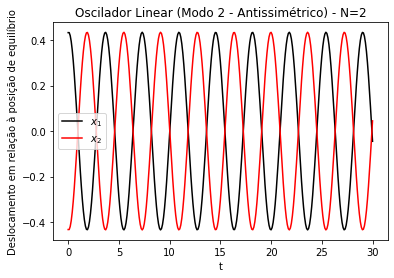
Alguns resultados das simulações para os modos desse caso podem ser observados na Figura 2 e na Figura 3. Fica evidente a menor frequência do modo simétrico em relação ao modo antissimétrico. Além disso, podemos observar a concordância com os valores teóricos encontrados para as frequências: $\omega _{1}=1$ e $\omega _{2}={\sqrt {3}}$. O modo simétrico consiste em uma oscilação em que as partículas estão em fase; no modo antissimétrico, as partículas oscilam fora de fase.

• 

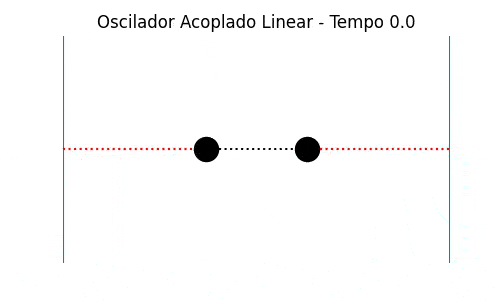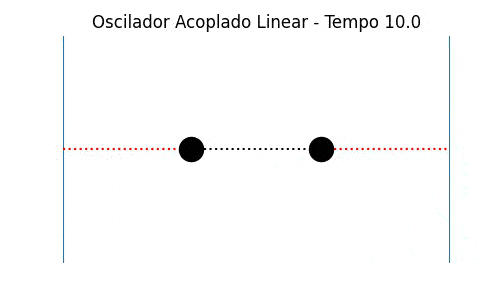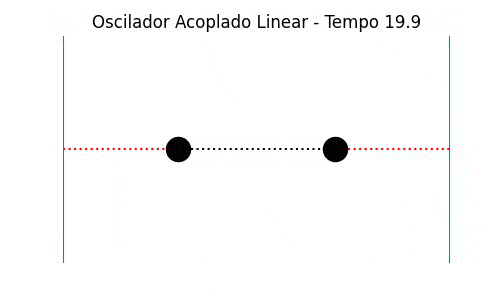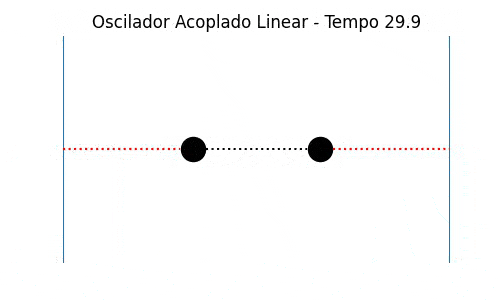
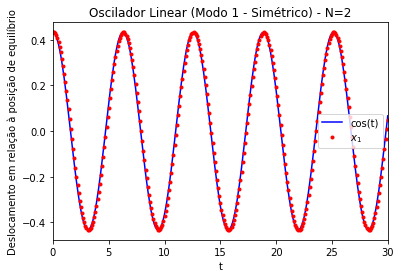
  Figura 2. Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta no gráfico, partícula da esquerda na simulação ao lado) e 2 (pontos vermelhos no gráfico, partícula da direita na simulação ao lado). k=m=1. Amplitude inicial de ~0.433. N=2

• 

  Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=2

• 

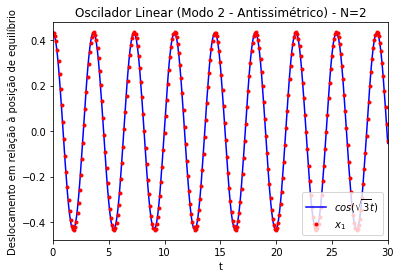
  Figura 3.Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta, partícula da esquerda na simulação ao lado) e 2 (pontos vermelhos, partícula da direita na simulação ao lado). k=m=1. Amplitude inicial de ~0.433. N=2

• 

  Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=2

A concordância das frequências com os valores teóricos calculados pode ser vista na Figura 4 e na Figura 5. Podemos observar a concordância com os valores teóricos encontrados para as frequências: $\omega _{1}=1$ e $\omega _{2}={\sqrt {3}}$.

• 

  Figura 4. Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1 (esquerda na simulação acima), conforme integração numérica (pontos vermelhos), em relação ao valor teórico (linha azul). k=m=1. Amplitude inicial de ~0.433. N=2

• 

  Figura 5. Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1 (esquerda na simulação acima), conforme integração numérica (pontos vermelhos), em relação ao valor teórico (linha azul). Amplitude inicial de ~0.433. k=m=1. Amplitude inicial de ~0.433. N=2

N=3

Seguindo a mesma lógica apresentada para $N=2$ partículas, podemos montar as equações de movimento do sistema com $N=3$ partículas. A única diferença é que a partícula central apenas está conectada a partículas vizinhas, não estando conectada a paredes externas:

${\begin{aligned}m{\ddot {x}}_{1}&=-kx_{1}-k(x_{1}-x_{2})\\m{\ddot {x}}_{2}&=-k(x_{2}-x_{1})-k(x_{2}-x_{3})\\m{\ddot {x}}_{3}&=-kx_{3}-k(x_{3}-x_{2})\quad (7)\\\end{aligned}}$

Supondo soluções do tipo

${\begin{aligned}x_{1}(t)&=A_{1}e^{-i\omega t}\\x_{2}(t)&=A_{2}e^{-i\omega t}\\x_{3}(t)&=A_{3}e^{-i\omega t}\quad (8)\end{aligned}}$

Substituindo (8) em (7) e seguindo os mesmos passos feitos para $N=2$ partículas:

${\begin{aligned}(2k-mw^{2})A_{1}&-kA_{2}&+0A_{3}&=0\\-kA_{1}&+(2k-mw^{2})A_{2}&-kA_{3}&=0\\0A_{1}&-kA_{2}&+(2k-mw^{2})A_{3}&=0\\\end{aligned}}$

O sistema de equações acima apenas terá soluções não triviais se o determinante dos coeficientes dos $A_{i}$ for igual a zero, i.e.:

${\begin{vmatrix}(2k-mw^{2})&-k&0\\-k&(2k-mw^{2})&-k\\0&-k&(2k-mw^{2})\end{vmatrix}}=0$

A equação resultante é $(2k-m\omega ^{2})^{3}-2k^{2}(2k-m\omega ^{2})=0$. Simples de ser resolvida analiticamente por fatoração, esta equação tem as soluções:

${\begin{aligned}\omega _{1}={\sqrt {{\frac {k}{m}}(2-{\sqrt {2}})}}\quad \quad \omega _{2}={\sqrt {\frac {2k}{m}}}\quad \quad \omega _{3}={\sqrt {{\frac {k}{m}}(2+{\sqrt {2}})}}\quad (9)\end{aligned}}$

Note-se que aqui já não é mais tão simples identificar as coordenadas normais. Além disso, embora tenha sido simples até aqui obter as autofrequências, o processo é tedioso e a equação característica pode ser difícil de se resolver analiticamente.

Podemos escrever as soluções da seguinte forma, de modo semelhante a como fizemos para $N=2$:

${\begin{aligned}x_{1}(t)=a_{1}^{1}e^{i\omega _{1}t}&+a_{1}^{2}e^{-i\omega _{1}t}&+a_{1}^{3}e^{i\omega _{2}t}&+a_{1}^{4}e^{-i\omega _{2}t}&+a_{1}^{5}e^{i\omega _{3}t}&+a_{1}^{6}e^{-i\omega _{3}t}\\x_{2}(t)=a_{2}^{1}e^{i\omega _{1}t}&+a_{2}^{2}e^{-i\omega _{1}t}&+a_{2}^{3}e^{i\omega _{2}t}&+a_{2}^{4}e^{-i\omega _{2}t}&+a_{2}^{5}e^{i\omega _{3}t}&+a_{2}^{6}e^{-i\omega _{3}t}\\x_{3}(t)=a_{3}^{1}e^{i\omega _{1}t}&+a_{3}^{2}e^{-i\omega _{1}t}&+a_{3}^{3}e^{i\omega _{2}t}&+a_{3}^{4}e^{-i\omega _{2}t}&+a_{3}^{5}e^{i\omega _{3}t}&+a_{3}^{6}e^{-i\omega _{3}t}\quad (10)\end{aligned}}$

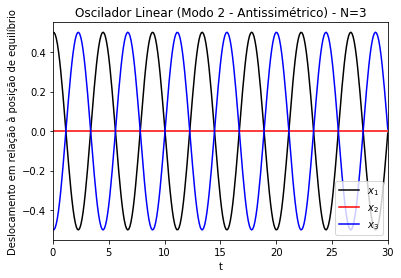
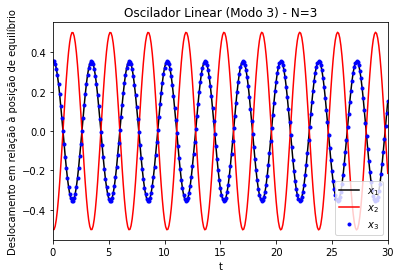
Alguns resultados das simulações para os modos desse caso podem ser observados na Figura 6, na Figura 7 e na Figura 8. Note-se a menor frequência do modo simétrico em relação aos demais modos. O modo simétrico consiste em uma oscilação em que todas as partículas estão em fase; no modo antissimétrico, as partículas 1 e 3 oscilam fora de fase, a 2 permanece parada. A novidade em relação ao caso de $N=2$ é o surgimento de um novo modo, o modo 3, em que as partículas 1 e 3 oscilam em fase, e a partícula 2 oscila fora de fase em relação às partículas 1 e 3.

• 

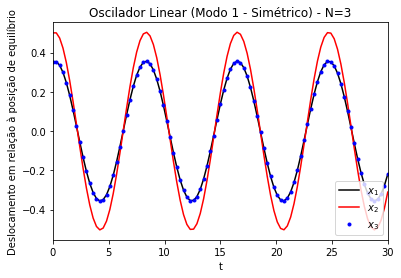
  Figura 6. Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta), 2 (linha vermelha) e 3 (pontos azuis). k=m=1. Amplitude inicial de ~ 0.35 para as partículas 1 e 3, e ~0.5 para a partícula 2. N=3

• 

  Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas.

• 

  Figura 7. Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta), 2 (linha vermelha) e 3 (linha azul). k=m=1. Amplitude inicial de ~ 0.5 para as partículas 1 e 3. N=3

• 

  Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas.

• 

  Figura 8. Modo de oscilação 3 de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta), 2 (linha vermelha) e 3 (pontos azuis). k=m=1. Amplitude inicial de ~ 0.35 para as partículas 1 e 3, e ~0.5 para a partícula 2. N=3

• 

  Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas.

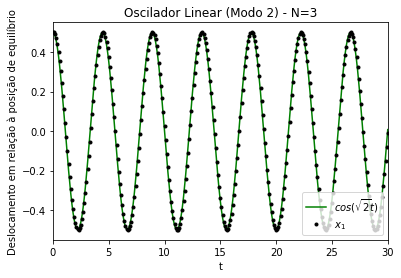
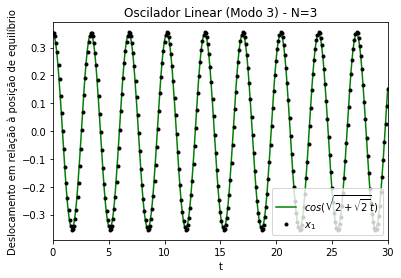
A concordância das frequências com os valores teóricos calculados pode ser vista na Figura 9, na Figura 10 e na Figura 11. Podemos observar a concordância com os valores teóricos encontrados para as frequências: $\omega _{1}={\sqrt {2-{\sqrt {2}}}}$, $\omega _{2}={\sqrt {2}}$ e $\omega _{3}={\sqrt {2+{\sqrt {2}}}}$.

• 

  Figura 9. Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1, conforme integração numérica (pontos pretos), em relação ao valor teórico (linha verde). k=m=1. Amplitude inicial de ~ 0.35. N=3

• 

  Figura 10. Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1, conforme integração numérica (pontos pretos), em relação ao valor teórico (linha verde). k=m=1. Amplitude inicial de ~ 0.5. N=3

• 

  Figura 11. Modo de oscilação 3 de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1, conforme integração numérica (pontos pretos), em relação ao valor teórico (linha verde). k=m=1. Amplitude inicial de ~ 0.35. N=3

Caso geral

O formalismo lagrangeano fornece uma técnica poderosa para encontrar as coordenadas normais, bem como as autofrequências [inserir referências]. No entanto, no presente trabalho, não precisamos fazer uso do formalismo lagrangeano. Será suficiente tratar o problema por análise de Fourier.

Podemos generalizar, para o caso de um N qualquer maior que 3, e obter as seguintes equações de movimento:

$m{\ddot {x}}_{i}={\begin{cases}-kx_{1}-k(x_{1}-x_{2}){\text{,}}&\quad {\text{se}}\quad i=1\\-k(x_{i}-x_{i-1})-k(x_{i}-x_{i+1}){\text{,}}&\quad {\text{se}}\quad 1<i<N\\-kx_{N}-k(x_{N}-x_{N-1}){\text{,}}&\quad {\text{se}}\quad i=N\quad \quad (11)\\\end{cases}}$

O conjunto de equações (11) vai ser importante para a implementação numérica.

As soluções (5) e (10) apresentam um padrão. Se tomarmos apenas as partes reais das soluções, podemos redefinir as constantes duas a duas e escrever a solução geral como:

${\begin{aligned}x_{l}(t)&=\sum _{m=1}^{N}a_{m}^{l}\cos(\omega _{m}t){\text{,}}\quad {\text{com}}\quad l=1{\text{,}}\,{\text{...}}{\text{,}}\,N\quad \\\end{aligned}}$

As constantes $a_{m}^{l}$ são chamadas de amplitudes dos modos normais e indicam o quanto de cada modo normal, de frequência bem definida, está presente na solução de cada $x_{l}(t)$. É possível mostrar (o que não faremos aqui por razões de tempo e espaço, mas pode ser consultado nas referências ) que, usando condições de contorno $x_{0}(t)=x_{N+1}(t)=0$, as soluções podem ser reescritas como

${\begin{aligned}x_{l}(t)&=\sum _{m=1}^{N}c_{m}\sin \left({\frac {lm\pi }{N+1}}\right)\cos(w_{m}t){\text{, com}}\quad l=1{\text{,}}\,{\text{...}}{\text{,}}\,N\quad (12)\\\end{aligned}}$

É comum na literatura redefinir a constante $c_{m}$ da seguinte forma:

${\begin{aligned}x_{l}(t)&={\sqrt {\frac {2}{N+1}}}\sum _{m=1}^{N}a_{m}\sin \left({\frac {lm\pi }{N+1}}\right)\cos(w_{m}t){\text{, com}}\quad l=1{\text{,}}\,{\text{...}}{\text{,}}\,N\\\end{aligned}}$

A qualquer instante de tempo, os deslocamentos das partículas em relação às posições de equilíbrio podem ser escritos como uma soma de modos normais. Esses modos normais são ondas estacionárias. Ver, por exemplo, a Figura 12, com os cinco primeiros modos.

Figura 12. Cinco primeiros modos de oscilação para um oscilador acoplado com N=32 partículas. Os gráficos correspondem à equação (12), no tempo $t=0$, com $c_{m}=1$.

É possível, portanto, por uma transformada inversa, escrever

${\begin{aligned}a_{m}&={\sqrt {\frac {2}{N+1}}}\sum _{i=1}^{N}x_{i}\sin \left({\frac {im\pi }{N+1}}\right){\text{, com}}\quad m=1{\text{,}}\,{\text{...}}{\text{,}}\,N\\\end{aligned}}\quad (13)$

As energias de cada modo podem ser escritas como (com ${\dot {a}}_{m}$ representando a amplitude da velocidade do modo):

${\begin{aligned}E_{m}&={\frac {1}{2}}\left[\left({\dot {a}}_{m}^{2}+\omega _{m}^{2}a_{m}^{2}\right)\right]\quad (14)\end{aligned}}$

E as frequências podem ser calculadas por (uma demonstração pode ser encontrada nas referências, supõe-se que as frequências dos modos são menores ou iguais a duas vezes a frequência natural, $\omega _{m}\leq 2\omega _{0}=2{\sqrt {k/m}}$ ):

${\begin{aligned}\omega _{m}&=2\omega _{0}\sin \left({\frac {m\pi }{2(N+1)}}\right)\quad (15)\end{aligned}}$

Todas as expressões mostradas nesta seção são válidas mesmo para o caso de oscilações acopladas não lineares, como é o caso do FPUT. [adicionar mais referências]

Podemos comparar, por exemplo, os valores que encontramos para as autofrequências nos casos $N=2$ e $N=3$ com os resultados da equação (15). Seja, por exemplo, $k=m=1$. Para $N=2$, pelas expressões (4), $\omega _{1}=1$ e $\omega _{2}={\sqrt {3}}$, que são os mesmos resultados fornecidos pela equação (15). De modo semelhante, para $N=3$, pelas expressões (9), $\omega _{1}={\sqrt {2-{\sqrt {2}}}}$, $\omega _{2}={\sqrt {2}}$ e $\omega _{3}={\sqrt {2+{\sqrt {2}}}}$, que também são os mesmos resultados fornecidos pela equação (15).

Adição de Termos Não-Lineares: Problema de FPUT

Como já discutido, se as forças em um sistema de osciladores acoplados forem todas da forma da lei de Hooke, o sistema jamais alcançará o equilíbrio térmico, pois os modos têm independência linear entre si. Para fazer isso, temos de acrescentar termos não-lineares de interação. Vamos tratar aqui o primeiro caso estudado no artigo original, em que os termos não-lineares são quadráticos nas coordenadas $x_{i}$.

Para os osciladores internos, teremos então a seguinte equação de movimento:

$m{\ddot {x}}_{i}=k_{1}\left[(x_{i+1}-x_{i})+(x_{i-1}-x_{i})\right]+k_{2}\left[(x_{i+1}-x_{i})^{2}-(x_{i-1}-x_{i})^{2}\right]$

Nessa equação, a constante $k_{1}$ faz o papel da constante das molas $k$ apresentada anteriormente para o caso puramente linear, enquanto $k_{2}$ informa a intensidade da força não-linear. É importante ressaltar que nem todos os autores definem os termos quadráticos dessa forma. Atualmente é mais comum ver esses termos definidos como faz, por exemplo, Lucero et al., 2021, que usa o sinal positivo entre os termos quadráticos, no interior dos colchetes. Podemos isolar a aceleração ${\ddot {x}}_{i}$ nesta equação; vamos escolher $k_{1}/m=1$ e definir $\alpha \equiv k_{2}/m$. A equação fica então:

${\ddot {x}}_{i}=(x_{i+1}-x_{i})+(x_{i-1}-x_{i})+\alpha \left[(x_{i+1}-x_{i})^{2}-(x_{i-1}-x_{i})^{2}\right]$

Esperava-se teoricamente que, pelo Teorema de Equipartição da Energia, o comportamento desse sistema seria a termalização. Isso significa que, diferentemente dos sistemas lineares, em que, iniciado em um modo, o sistema permanece naquele modo para todo tempo $t>0$ (como podemos perceber nas simulações apresentadas acima para diversos modos com $N=1,\,{\text{...}},\,5$) [inserir referência da própria wiki], o sistema tenderia a se tornar uma mistura complicada de modos a partir de um determinado tempo, e permanecer nesse estado. Uma análise normalmente é feita por meio de gráficos da distribuição de energia entre os modos.

Quando o sistema é linear, a energia total do sistema se reduz a uma soma $E=\sum _{k}^{N}E_{k}$ das energias de cada modo. Essas energias são integrais do movimento, o que leva a $E_{k}(t)=E_{k}(0)$. Quando há termos não lineares, as energias dos modos normais não são mais integrais do movimento e um argumento de mecânica estatística sugere que as médias temporais das energias de cada modo,$E_{k}(t)=(1/t)\int _{0}^{t}E_{k}(\tau )d\tau$ , deveriam tender a um mesmo valor [inserir referências].

O paradoxo ou problema de FPUT consiste em um comportamento de recorrência que não era esperado. Como pode ser observado nas simulações [inserir referência da própria wiki], após um determinado tempo, o sistema volta ao modo em que o

Implementação numérica

$m{\ddot {x}}_{i}={\begin{cases}-kx_{1}-k(x_{1}-x_{2}){\text{,}}&\quad {\text{se}}\quad i=1\\-k(x_{i}-x_{i-1})-k(x_{i}-x_{i+1}){\text{,}}&\quad {\text{se}}\quad 1<i<N\\-kx_{N}-k(x_{N}-x_{N-1}){\text{,}}&\quad {\text{se}}\quad i=N\quad \quad (11)\\\end{cases}}$

Simulações

Osciladores Lineares Acoplados

N=2

• 

  Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=2

• 

  Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=2

N=3

• 

  Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas.

• 

  Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas.

• 

  Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas.

N=4

Embora não tenhamos feito análises para os casos de N=4 e N=5 partículas, abaixo seguem simulações dos modos desses osciladores acoplados lineares unidimensionais. Observa-se o mesmo padrão de aumento da frequência com o número do modo. O modo simétrico sempre apresenta menor frequência.

• 

  Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=4

• 

  Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=4

• 

  Modo de oscilação 3 de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=4

• 

  Modo de oscilação 4 de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=4

N=5

• 

  Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=5

• 

  Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=5

• 

  Modo de oscilação 3 de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=5

• 

  Modo de oscilação 4 de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=5

• 

  Modo de oscilação 5 de um oscilador linear acoplado unidimensional, simulado com k=m=1 para todas as massas e molas. N=5

Bidimensional N=49 (Em um grid 7x7)

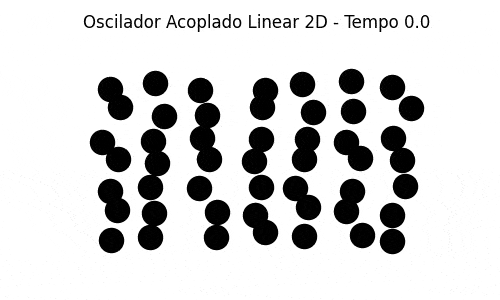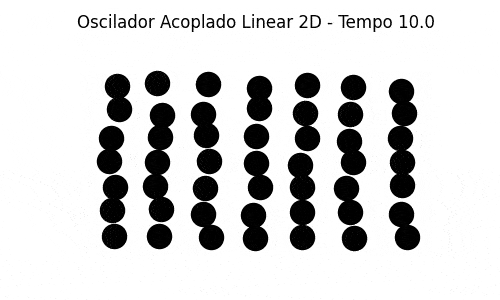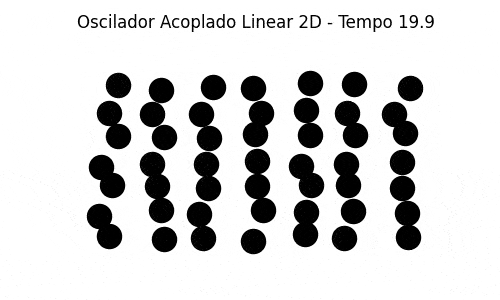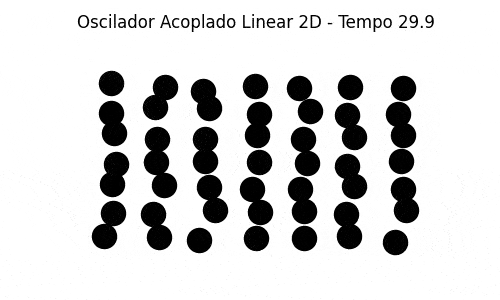
Também implementamos uma simulação bidimensional de massas acopladas com as partículas vizinhas de cima, de baixo e dos lados. As partículas das fronteiras estão conectadas às paredes (em cima, embaixo e dos lados). A generalização do caso unidimensional é direta e foi razoavelmente simples de se implementar, uma vez estabelecida a condição inicial (colocar as partículas nas posições de equilíbrio, espaçadas igualmente em um grid, e deslocar randomicamente cada uma de sua posição de equilíbrio por um valor bem pequeno). A simulação mostra um comportamento que pode ser associado à dinâmica molecular.

• 

  Nessa simulação, usamos k=1 e m=6 para diminuir a força e evitar sobreposições entre as partículas.

FPUT quadrático

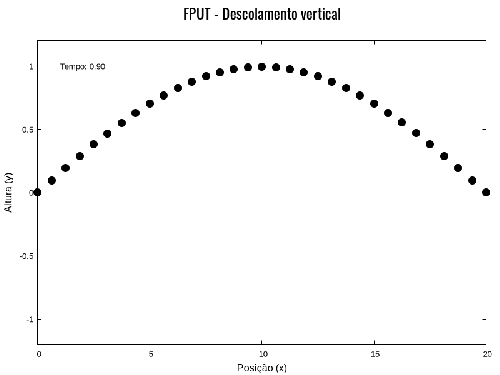
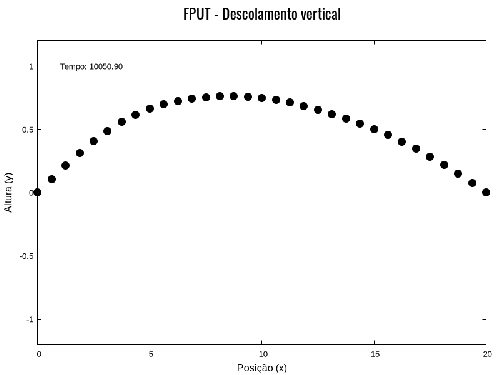
Abaixo segue uma simulação em que as partículas são deslocadas das posições de equilíbrio verticalmente. Esse modelo é muito interessante para visualizar a propriedade de recorrência ao primeiro modo, embora não seja um modelo muito físico, porque as partículas oscilam apenas na vertical, acopladas às partículas vizinhas. Não há deslocamento na horizontal, e a simulação é na verdade uma simulação unidimensional.

Parâmetros da simulação com deslocamento vertical: $k=1.0;m=1.0;\alpha =0.25;\Delta t=0.01;L=20.0;N=32$.

• 

  Figura X. Primeira parte da simulação do oscilador acoplado com N=32 partículas com deslocamento limitado a vertical. Nessa animação podemos ver as primeiras iterações após a condição inicial proposta no trabalho original.

• 

  Figura X. Segunda parte da simulação do oscilador acoplado com N=32 partículas com deslocamento limitado a vertical. Nessa animação vemos o sistema retornando a uma posição próxima da condição inicial.

Programa

• Código em C e scripts para FPUT com deslocamento vertical

• Código em Python para simulações de osciladores lineares e FPUT quadrático

Bibliografia principal

• Marion, J.B., Thornton, S.T. "Classical Dynamics of Particles and Systems". Thomson Learning, Belmont, 2004.
• Giordano, N.J., Nakanishi, H. "Computational Physics". 2nd Edition. Prentice Hall, Upper Saddle River, 2006.