Modelo Brusselator de Reação-Difusão

Grupo: Carolina Lenzi, Eric Naiber e Vitória Xavier

O objetivo deste trabalho é implementar o modelo de reação-difusão Brusselator em duas dimensões, frequentemente utilizado para estudar sistemas complexos químicos e biológicos. O modelo é um sistema não linear de equações diferenciais parciais e foi proposto em 1970 por Ilya Prigogine e seus colaboradores da Universidade Livre de Bruxelas. Desde então tem sido aplicado para analisar reações oscilatórias e autocatalíticas. O método computacional utilizado para implementar o modelo foi o método FTCS (Forward Time Centered Space).

Modelo de Brusselator

O estudo de sistemas químicos e biológicos frequentemente requer o uso de modelos que caracterizam reações de reação-difusão. Um dos modelos mais utilizados é o modelo de Brusselator, que é utilizado para descrever o mecanismo químico de reação-difusão com oscilações não lineares. . Turing [ref?] observou que quando determinadas reações são associadas a difusão, é possível obter um padrão espacial estável, e isso leva a teoria de morfogênese. Além de processos de reação-difusão, o modelo Brusselator é observado em reações enzimáticas e na física de plasma e de lasers.

O mecanismo de Brusselator proposto por Prigogine (1970) é dado por:

$A\to U$ (1.a)

$B+U\to V+D$ (1. b)

$2U+V\to 3U$ (1.c)

$U\to E$ (1.d)

Onde U e V são as espécies químicas de interesse. Assumimos A e B em excesso para que o sistema não atinja o equilíbrio. Esse sistema químico foi importante para o avanço na área de sistemas complexos porque possibilita o uso de modelos matemáticos de duas dimensões, já que U e V são variáveis dependentes, e admite “limit-cycle oscilations”. [ R. Lefever and G. Nicolis, Chemical instabilities and sustained oscillations, J. Theor. Biol. 30 (1971) 267.].

As equações diferenciais parciais associadas com o sistema Brusselator são dadas por(G. Adomian, The diffusion-Brusselator equation. Comput. Math. Appl. 29, 1–3 (1995)):

${\frac {\partial u}{\partial t}}=a+u^{2}v-(b+1)u+D_{u}\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}\right)$

${\frac {\partial v}{\partial t}}=bu-u^{2}v+D_{v}\left({\frac {\partial ^{2}v}{\partial x^{2}}}+{\frac {\partial ^{2}v}{\partial y^{2}}}\right)$

onde $u(x,y,t)$ e $v(x,y,t)$ são as concentrações a serem investigadas em função de tempo e espaço, $a$ e $b$ são constantes relativas às concentrações dos reagentes A e B, e $D_{u}$ e $D_{v}$ constantes de difusão.

A solução analítica do sistema reação-difusão Brusselator ainda não é conhecida e por isso há o interesse de explorá-la numericamente.

Análise da estabilidade do sistema

Análise de ponto crítico

Considerando o sistema livre de difusão, quando $\partial x=\partial y=0$:

${\frac {du}{dt}}=f(u,v)=a+u^{2}v-(b+1)u\qquad t<0\quad u(0)=U^{0}$

${\frac {dv}{dt}}=g(u,v)=bu-u^{2}v\qquad \qquad \qquad \,\,t<0\quad v(0)=V^{0}$

Onde $u=u(t)$ e $v=v(t)$ e $a$ e $b$ são constantes positivas e reais. A matriz jacobiana $J^{*}$ no ponto crítico $(u^{*},v^{*})$ é dada por

$J^{*}={\begin{bmatrix}b-1&a^{2}\\-b&-a^{2}\end{bmatrix}}$

Os autovalores de $J^{*}$ são os valores $\lambda$ que satisfazem a equação caracterísitca

$\lambda ^{2}+(1-b+a^{2})\lambda +a^{2}=0$

Os autovalores claramente mostram dependência em $1-b+a^{2}$ e no determinante $\Delta =(1-b+a^{2})^{2}-4a^{2}$. Esses autovalores governam a estabilidade do ponto crítico ou determinam a existência de um ciclo limite. As propriedades de estabilidade ou a existência de um ciclo limite estão sumarizadas na tabela abaixo, em relação a figura 1.

[[Arquivo:]]

Utilizando a teoria Hopf, é mostrado que o ponto crítico perde sua estabilidade quando A e B movem da região 2 para região 3, na figura 1, atravessando a curva $1-b+a^{2}=0$. Uma bifurcação Hopf ocorre quando ao passo que essa curva é atravessada e um ciclo limite estável existe para A e B nas regiões 1 e 2, mas não para A e B nas regiões 3 e 4.

Conclui-se que a curva $1-b+a^{2}=0$ governa a estabilidade do sistema.

Análise de ponto fixo

O estado estacionário do sistema pode ser encontrado igualando o coeficiente de difusão, e portanto as derivadas parciais, a zero. Percebe-se que esse sistema converge para os pontos fixos:

$u=a$

$v={\frac {b}{a}}$

Em [twizell] a manipulação da matriz jacobiana nos pontos fixos resulta nos seguintes autovalores

$\mu _{1}={\frac {1+{\frac {1}{2}}\ell (1-b+a^{2})-{\frac {1}{4}}\ell ^{2}a^{2}}{1+{\frac {1}{2}}\ell (1-b+a^{2})+{\frac {1}{4}}\ell ^{2}a^{2}}}$

$\mu _{2}={\frac {1-{\frac {1}{2}}\ell (1-b+a^{2})-{\frac {1}{4}}\ell ^{2}a^{2}}{1+{\frac {1}{2}}\ell (1-b+a^{2})+{\frac {1}{4}}\ell ^{2}a^{2}}}$

Onde fica claro que os denominadores dos autovalores são sempre positivos quando $1-b+a^{2}>0$ and $\ell >0$. As inequações

$|\mu _{1}|<1\quad$ e $\quad |\mu _{2}|<1$

São verdadeiras sempre que $1-b+a^{2}=0$. Portanto, uma condição suficiente para o ponto fixo $\left(a,{\frac {b}{a}}\right)$ atrair a sequência gerada pelo sistema é $1-b+a^{2}>0$.

Ainda em [Twizell] o modelo reação-difusão Brusselator foi discretizado e a análise dos pontos fixos concluiu que o sistema converge para $u(x,t)=a$ e $v(x,t)={\frac {b}{a}}$, sendo esse o único estado estacionário do sistema.

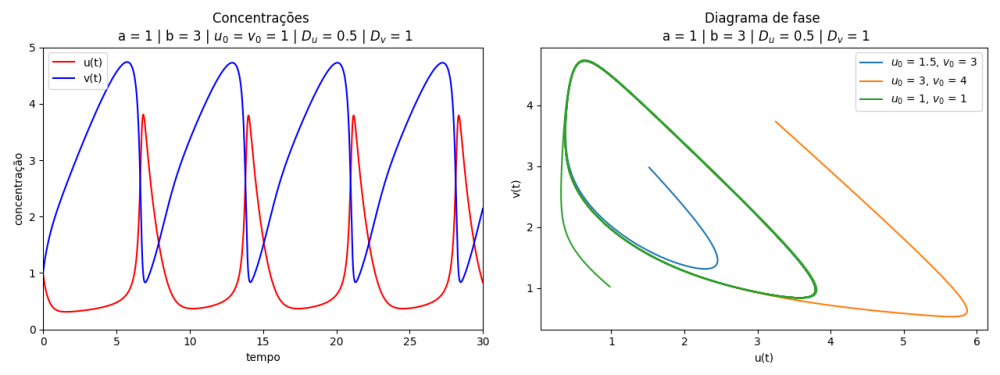
Concluiu que também que o sistema apresenta estado oscilatório quando

$1-b+a<0$

Estado em que o sistema não converge para nenhum ponto.

Método FTCS

O FTCS (Forward Time Centered Space) é um método de diferença finita que utiliza a derivada à direita ("para frente") no tempo e a derivada segunda centralizada no espaço para discretizar as variáveis. As derivadas no tempo e no espaço bidimensional ficam:

${\frac {\partial f(x,y,t)}{\partial t}}\to {\frac {f(x,y,t+\Delta t)-f(x,y,t)}{\Delta t}}+{\mathcal {O}}(\Delta t^{2})$

${\frac {\partial ^{2}f(x,y,t)}{\partial x^{2}}}\to {\frac {f(x-\Delta x,y,t)-2f(x,y,t)+f(x+\Delta x,y,t)}{(\Delta x)^{2}}}+{\mathcal {O}}(\Delta x^{3})$

${\frac {\partial ^{2}f(x,y,t)}{\partial y^{2}}}\to {\frac {f(x,y-\Delta y,t)-2f(x,y,t)+f(x,y+\Delta y,t)}{(\Delta y)^{2}}}+{\mathcal {O}}(\Delta y^{3})$

Substituindo nas equações do Brusselator

${\frac {u(x,y,t+\Delta t)-u(x,y,t)}{\Delta t}}=f(u,v)+D_{u}\left({\frac {u(x-\Delta x,y,t)-2u(x,y,t)+u(x+\Delta x,y,t)}{(\Delta x)^{2}}}+{\frac {u(x,y-\Delta y,t)-2u(x,y,t)+u(x,y+\Delta y,t)}{(\Delta y)^{2}}}\right)$

${\frac {v(x,y,t+\Delta t)-v(x,y,t)}{\Delta t}}=g(u,v)+D_{v}\left({\frac {v(x-\Delta x,y,t)-2v(x,y,t)+v(x+\Delta x,y,t)}{(\Delta x)^{2}}}+{\frac {v(x,y-\Delta y,t)-2v(x,y,t)+v(x,y+\Delta y,t)}{(\Delta y)^{2}}}\right)$

onde $f(u,v)$ e $g(u,v)$ são as funções que representam a reação sem difusão.

Utilizamos discretização do tipo

$t=0,1\Delta t,2\Delta t,3\Delta t,...,t_{max}$

$x=0,1\Delta x,2\Delta x,3\Delta x,...,N_{x}$

$y=0,1\Delta y,2\Delta y,3\Delta y,...,N_{y}$

Utilizando a notação $f(i\Delta x,j\Delta y,n\Delta t)=f_{i,j}^{n}$, assumindo $\Delta x=\Delta y=\Delta s$ e rearranjando os termos, reescrevemos as equações como

$u_{i,j}^{n+1}=u_{i,j}^{n}+f(u_{i,j}^{n},v_{i,j}^{n})\Delta t+K_{u}(u_{i-1,j}^{n}+u_{i+1,j}^{n}+u_{i,j-1}^{n}+u_{i,j+1}^{n}-4u_{i,j}^{n})$

$v_{i,j}^{n+1}=v_{i,j}^{n}+g(u_{i,j}^{n},v_{i,j}^{n})\Delta t+K_{v}(v_{i-1,j}^{n}+v_{i+1,j}^{n}+v_{i,j-1}^{n}+v_{i,j+1}^{n}-4v_{i,j}^{n})$

onde $K_{u}={\frac {D_{u}\Delta t}{(\Delta s)^{2}}}$ e $K_{v}={\frac {D_{v}\Delta t}{(\Delta s)^{2}}}$.

Análise de estabilidade

A análise de estabilidade do método FTCS pode ser feita com a análise local de von Neumann. Para isso precisamos linearizar as equações do modelo Brusselator e escrever as soluções em modos de Fourier, da seguinte forma:

$\delta u_{i,j}^{n+1}=\delta u_{i,j}^{n}+K_{u}\left(\delta u_{i+1,j}^{n}+\delta u_{i-1,j}^{n}\delta u_{i,j+1}^{n}+\delta u_{i,j-1}^{n}-4\delta u_{i,j}^{n}\right)+\Delta tf_{u}\delta u_{i,j}^{n}+\Delta tf_{v}\delta v_{i,j}^{n}$

$\delta v_{i,j}^{n+1}=\delta v_{i,j}^{n}+K_{v}\left(\delta v_{i+1,j}^{n}+\delta v_{i-1,j}^{n}\delta v_{i,j+1}^{n}+\delta v_{i,j-1}^{n}-4\delta v_{i,j}^{n}\right)+\Delta tg_{u}\delta u_{i,j}^{n}+\Delta tg_{v}\delta v_{i,j}^{n}$

${\delta u^{n} \choose \delta v^{n}}=A^{n}e^{i(k_{x}i\Delta x+k_{y}j\Delta y)}{\delta u_{0} \choose \delta v_{0}}$

Para que o método seja estável, é preciso que $|A|<1$. Após inserir as soluções nas equações linearizadas e realizar manipulações algébricas, como feito por Scholz (2009), obtemos

$A_{\pm }={\frac {1}{2}}\left[\beta \pm {\sqrt {\beta ^{2}-4(\Delta t)^{2}a^{2}b}}\right]$

onde

$\beta =2-4\gamma (K_{u}+K_{v})+\Delta t(b-1-a^{2})$

e

$\gamma =sin^{2}\left({\frac {k_{x}\Delta s}{2}}\right)+sin^{2}\left({\frac {k_{y}\Delta s}{2}}\right)$

Os valores $\Delta t=0.01$ e $\Delta s=1$ satisfazem a condição de estabilidade, como mostrado em .

Implementação

O método foi implementado em Python, utilizando as constantes definidas na tabela abaixo.

Os valores de $b$ e as condições iniciais foram variados, como descrito na seção de resultados.

A seguir, o trecho do código relativo à implementação do método. O código completo, com a geração dos gráficos, encontra-se no Github [1]

#Nx = Ny -> Tamanho do recipiente

    while t < t_max:

        for i in range(Nx):
            i_e = (i - 1) % Nx  # vizinho a esquerda de 0 é o da ultima posicao
            i_d = (i + 1) % Nx  # vizinho a direita da ultima posicao é o zero

            for j in range(Ny):
                j_e = (j - 1) % Ny
                j_d = (j + 1) % Ny

                u_n1[i, j] = u_n[i, j] + dt * f(u_n[i, j], v_n[i, j], b) \
                             + ku * (u_n[i_e, j] + u_n[i_d, j] + u_n[i, j_e] + u_n[i, j_d] - 4 * u_n[i, j])
                v_n1[i, j] = v_n[i, j] + dt * g(u_n[i, j], v_n[i, j], b) \
                             + kv * (v_n[i_e, j] + v_n[i_d, j] + v_n[i, j_e] + v_n[i, j_d] - 4 * v_n[i, j])

        # atualizar u_n e v_n
        for i in range(Nx):
            for j in range(Ny):
                u_n[i, j] = u_n1[i, j]
                v_n[i, j] = v_n1[i, j]

        t += dt

Resultados

Esta seção se dedica ao resultados das simulações realizadas, que mostram o caráter oscilatório do Brusselator ao longo do tempo e também como se dá a difusão dos reagentes em um recipiente em duas dimensões. As constantes utilizadas foram identificadas abaixo para plotar os gráficos (exceto quando indicado o contrário).

Tabela de Constantes e Valores
Símbolo	Nome	Valor
$N_{x}$	Dimensão analisada ao longo do eixo x	50
$N_{y}$	Dimensão analisada ao longo do eixo y	50
$a$	Constante relativa à concentração do reagente A	1
$b$	Constante relativa à concentração do reagente B	-
$D_{u}$	Constante de difusão do reagente U	0.5
$D_{v}$	Constante de difusão do reagente V	1
$u_{0}$	Concentração de u no tempo inicial (t=0)	-
$v_{0}$	Concentração de v no tempo inicial (t=0)	-
$dt$	Passo de tempo entre iterações	0.01
$ds$	Unidade de avanço dos eixos no espaço	1

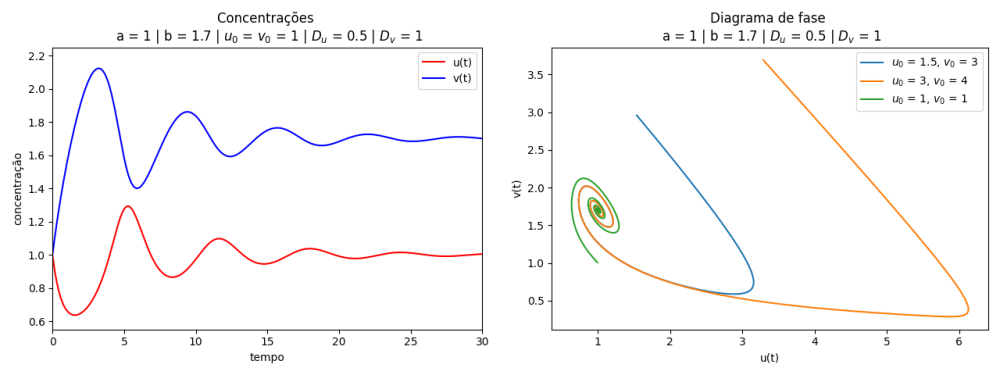
Na figura abaixo, as soluções do Brusselator e os diagramas de fase, variando $b$ e as condições iniciais.

Figura 1: Gráfico de concentrações.

Figura 1: Gráfico de concentrações.

As posições das condições iniciais foram escolhidas arbitrariamente, tendo um total de 6 modos que serão explicados logo à frente, sendo eles:

1. Condição em formato do sinal "+".
2. Condição de borda.
3. Condição aleatória.
4. Condição de nove pontos centrais.
5. Condição da borda completa.

Simulação

No gráfico abaixo podemos notar o caráter ondulatório da variação da concentração ao longo do tempo, as linhas (azul e vermelho) significam a taxa de concentração no recipiente.

Note que quando $U$ diminui, $V$ aumenta rapidamente, mantendo-se um ciclo oscilatório em que a amplitude das ondas de $U$ e $V$ vai diminuindo ao longo do tempo, como mostrado nas figuras.

Pensando no gráfico da reação-difusão como ondas, é correto afirmar que ambas juntas formam um padrão de interferência destrutivo. A animação abaixo mostra exatamente este comportamento, observando o reagente $U$ no gráfico da direita. Note que quando o ponto do gráfico da esquerda chega ao mínimo local, o valor de $U$ é alto e o de $V$ muito baixo, fazendo com que o gráfico da direita fique muito amarelo (amarelo significa uma alta concentração de $U$ sendo formada).

Figura 2:: Comportamento do reagente.

---

Condições Iniciais

Para observar melhor os resultados, foram feitas diversas condições iniciais que foram separadas em tópicos citados em Definindo Constantes.

Levando em consideração que u_n é um array de tamanho $N_{x}$ por $N_{y}$.

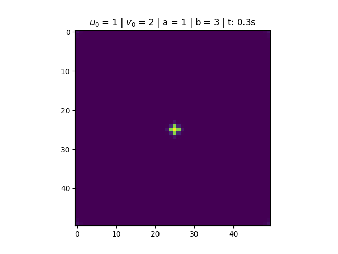
Condição em Formato do Sinal "+"

O reagente $u_{0}$ é distribuído no centro formando um sinal de "+".

Figura 3:: Comportamento em formato de "+" para o reagente u. Para o reagente v foi utilizado a condição de borda.

# u_n [Nx, Ny]

# Centro
u_n[int(Nx / 2), int(Ny / 2)] = u0


# Lateral do sinal
#       X                   Y
u_n[int(Nx / 2) + 1, int(Ny / 2)] = u0
u_n[int(Nx / 2) - 1, int(Ny / 2)] = u0


# Altura do sinal
#       X                   Y
u_n[int(Nx / 2), int(Ny / 2) + 1] = u0
u_n[int(Nx / 2), int(Ny / 2) - 1] = u0

---

Condição de borda

O reagente $v_{0}$ foi distribuído nos 4 cantos do recipiente.

Figura 4:: Analisando u com condição de borda "+". Para o reagente v foi utilizado a condição de borda. Foi utilizado b=3 para mostrar a diferença na simulação.

# u_n [Nx, Ny]

# Sup Esq
v_n[0, 0] = v0


# Sup Dir
v_n[0, Nx - 1] = v0


# Inf Esq
v_n[Nx - 1, 0] = v0


# Inf Dir
v_n[Nx - 1, Nx - 1] = v0

---

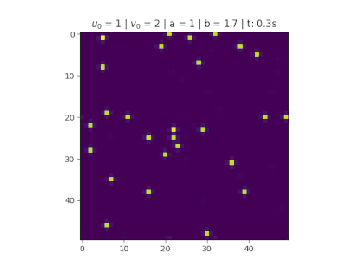
Condição aleatória

Os reagentes são aleatoriamente distribuídos ao longo do recipiente, a quantidade de focos de reagente também é aleatória para $u_{0}$ e $v_{0}$.

Figura 5:: Posição aleatória.

from random import *

# u_n [Nx, Ny]

aleatorio = randint(int(Nx / 5)


# Aleatório para u
for _ in range(aleatorio, Nx)):
    u_n[randint(0, size), randint(0, size)] = u0


# Aleatório para v
for _ in range(aleatorio, Nx)):
    v_n[randint(0, size), randint(0, size)] = v0

---

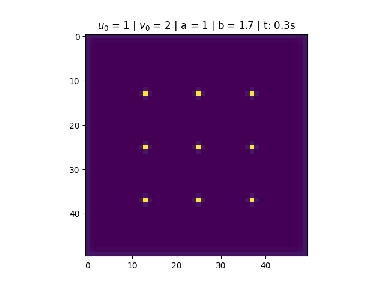
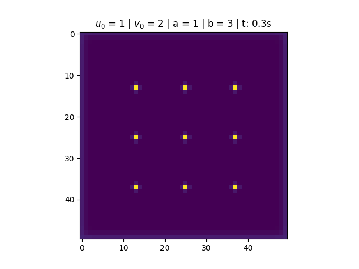
Condição de nove pontos centrais

Foi utilizado na figura 2.

No centro divide 9 pontos igualmente espaçados de tamanho $N_{x}/4$, para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_0} .

Figura 6:: Utilizando a condição de borda para v.

# Nove pontos centrais (u0)
mid = int(Nx / 2); mov = int(Nx / 4)

# Meio & direita
u_n[mid, mid] = u0
u_n[mid + mov, mid + mov] = u0
# Meio & esquerda
u_n[mid + mov, mid] = u0
u_n[mid, mid + mov] = u0
# Meio, p/baixo & p/lados
u_n[mid + mov, mid - mov] = u0
u_n[mid - mov, mid - mov] = u0
# Meio, p/cima & p/lados
u_n[mid - mov, mid] = u0
u_n[mid, mid - mov] = u0
u_n[mid - mov, mid + mov] = u0

---

Condição da borda completa

Foi utilizado na figura 2.

Completa toda a borda do recipiente com reagente $v_{0}$.

Figura 7:: Utilizando a condição de borda para v e b=3.

# v_n = [Nx, Ny]


# Toda a borda (v0)


for i in range(Nx):

    # Completa primeira coluna e primeira linha
    v_n[0, i] = v0
    v_n[i, 0] = v0

    # Completa última coluna e última linha
    v_n[Nx - 1, i] = v0
    v_n[i, Nx - 1] = v0