Modelo Brusselator de Reação-Difusão

Grupo: Carolina Lenzi, Eric Naiber e Vitória Xavier

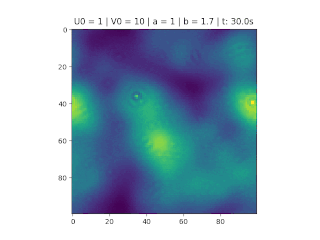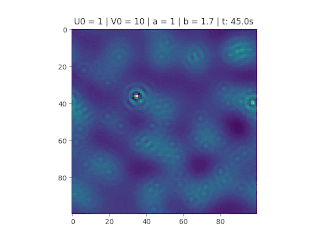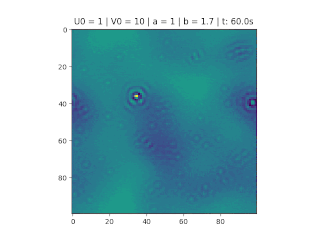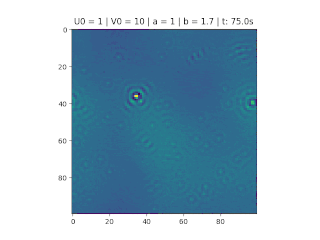
Figura 1: Variação da concentração em um recipiente de 100x100. Áreas em amarelo correspondem a uma grande quantidade de reagente U.

O objetivo deste trabalho é implementar o modelo de reação-difusão Brusselator em duas dimensões, frequentemente utilizado para estudar sistemas complexos químicos e biológicos. O modelo é um sistema não linear de equações diferenciais parciais e foi proposto em 1970 por Ilya Prigogine e seus colaboradores da Universidade Livre de Bruxelas. Desde então tem sido aplicado para analisar reações oscilatórias e autocatalíticas. O método computacional utilizado para implementar o modelo foi o método FTCS (Forward Time Centered Space).

Modelo de Brusselator

Figura 2: O gráfico da esquerda mostra a variação dos reagentes U e V dentro do sistema. Levando em consideração o gráfico "Reação-Difusão", note que quando U e V se anulam temos um mínimo no gráfico da esquerda. No gráfico da direita podemos perceber este comportamento, quando o ponto está em um mínimo, a quantidade de U sobe rapidamente, fazendo com que o gráfico fique com muitos pontos amarelos.

O estudo de sistemas químicos e biológicos frequentemente requer o uso de modelos que caracterizam reações de reação-difusão. Um dos modelos mais utilizados é o modelo de Brusselator, que é utilizado para descrever o mecanismo químico de reação-difusão com oscilações não lineares. [J. Tyson, Some further studies of nonlinear oscillations in chemical systems, J. Chem. Phys. 58 (1973) 3919.] Turing [ref?] observou que quando determinadas reações são associadas a difusão, é possível obter um padrão espacial estável, e isso leva a teoria de morfogênese. Além de processos de reação-difusão, o modelo Brusselator é observado em reações enzimáticas e na física de plasma e de lasers.

O mecanismo de Brusselator proposto por Prigogine (1970) é dado por [I. Prigogine, R. Lefever, Symmetries breaking instabilities in dissipative systems II. J. Phys. Chem. 48, 1695–1700 (1968)]:

$A\to U$ (1.a)

$B+U\to V+D$ (1. b)

$2U+V\to 3U$ (1.c)

$U\to E$ (1.d)

Onde U e V são as espécies químicas de interesse. Assumimos A e B em excesso para que o sistema não atinja o equilíbrio. Esse sistema químico foi importante para o avanço na área de sistemas complexos porque possibilita o uso de modelos matemáticos de duas dimensões, já que U e V são variáveis dependentes, e admite “limit-cycle oscilations”. [ R. Lefever and G. Nicolis, Chemical instabilities and sustained oscillations, J. Theor. Biol. 30 (1971) 267.].

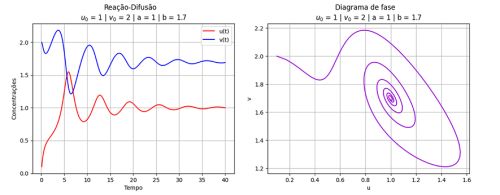
Figura 3: Relação entre concentrações e o diagrama de fase.

As equações diferenciais parciais associadas com o sistema Brusselator são dadas por(G. Adomian, The diffusion-Brusselator equation. Comput. Math. Appl. 29, 1–3 (1995)):

${\frac {\partial u}{\partial t}}=a+u^{2}v-(b+1)u+D_{u}\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}\right)$

${\frac {\partial v}{\partial t}}=bu-u^{2}v+D_{v}\left({\frac {\partial ^{2}v}{\partial x^{2}}}+{\frac {\partial ^{2}v}{\partial y^{2}}}\right)$

onde $u(x,y,t)$ e $v(x,y,t)$ são as concentrações a serem investigadas em função de tempo e espaço, $a$ e $b$ são constantes relativas às concentrações dos reagentes A e B, e $D_{u}$ e $D_{v}$ constantes de difusão.

A solução analítica do sistema reação-difusão Brusselator ainda não é conhecida e por isso há o interesse de explorá-la numericamente.

Análise da estabilidade do sistema

Análise de ponto crítico

Considerando o sistema livre de difusão, quando $\partial x=\partial y=0$:

${\frac {du}{dt}}=f(u,v)=a+u^{2}v-(b+1)u\qquad t<0\quad u(0)=U^{0}$

${\frac {dv}{dt}}=g(u,v)=bu-u^{2}v\qquad \qquad \qquad \,\,t<0\quad v(0)=V^{0}$

Onde $u=u(t)$ e $v=v(t)$ e $a$ e $b$ são constantes positivas e reais. A matriz jacobiana $J^{*}$ no ponto crítico $(u^{*},v^{*})$ é dada por

$J^{*}={\begin{bmatrix}b-1&a^{2}\\-b&-a^{2}\end{bmatrix}}$

Os autovalores de $J^{*}$ são os valores $\lambda$ que satisfazem a equação caracterísitca

$\lambda ^{2}+(1-b+a^{2})\lambda +a^{2}=0$

Os autovalores claramente mostram dependência em $1-b+a^{2}$ e no determinante $\Delta =(1-b+a^{2})^{2}-4a^{2}$. Esses autovalores governam a estabilidade do ponto crítico ou determinam a existência de um ciclo limite. As propriedades de estabilidade ou a existência de um ciclo limite estão sumarizadas na tabela abaixo, em relação a figura 1.

[[Arquivo:]]

Utilizando a teoria Hopf, é mostrado que o ponto crítico perde sua estabilidade quando A e B movem da região 2 para região 3, na figura 1, atravessando a curva $1-b+a^{2}=0$. Uma bifurcação Hopf ocorre quando ao passo que essa curva é atravessada e um ciclo limite estável existe para A e B nas regiões 1 e 2, mas não para A e B nas regiões 3 e 4.

Conclui-se que a curva $1-b+a^{2}=0$ governa a estabilidade do sistema.

Análise de ponto fixo

O estado estacionário do sistema pode ser encontrado igualando o coeficiente de difusão, e portanto as derivadas parciais, a zero. Percebe-se que esse sistema converge para os pontos fixos:

$u=a$

$v={\frac {b}{a}}$

Em [twizell] a manipulação da matriz jacobiana nos pontos fixos resulta nos seguintes autovalores

$\mu _{1}={\frac {1+{\frac {1}{2}}\ell (1-b+a^{2})-{\frac {1}{4}}\ell ^{2}a^{2}}{1+{\frac {1}{2}}\ell (1-b+a^{2})+{\frac {1}{4}}\ell ^{2}a^{2}}}$

$\mu _{2}={\frac {1-{\frac {1}{2}}\ell (1-b+a^{2})-{\frac {1}{4}}\ell ^{2}a^{2}}{1+{\frac {1}{2}}\ell (1-b+a^{2})+{\frac {1}{4}}\ell ^{2}a^{2}}}$

Onde fica claro que os denominadores dos autovalores são sempre positivos quando $1-b+a^{2}>0$ and $\ell >0$. As inequações

$|\mu _{1}|<1\quad$ e $\quad |\mu _{2}|<1$

São verdadeiras sempre que $1-b+a^{2}=0$. Portanto, uma condição suficiente para o ponto fixo $\left(a,{\frac {b}{a}}\right)$ atrair a sequência gerada pelo sistema é $1-b+a^{2}>0$.

Ainda em [Twizell] o modelo reação-difusão Brusselator foi discretizado e a análise dos pontos fixos concluiu que o sistema converge para $u(x,t)=a$ e $v(x,t)={\frac {b}{a}}$, sendo esse o único estado estacionário do sistema.

Concluiu que também que o sistema apresenta estado oscilatório quando

$1-b+a<0$

Estado em que o sistema não converge para nenhum ponto.

Método FTCS

O FTCS (Forward Time Centered Space) é um método de diferença finita que utiliza a derivada à direita ("para frente") no tempo e a derivada segunda centralizada no espaço para discretizar as variáveis. As derivadas no tempo e no espaço bidimensional ficam:

${\frac {\partial f(x,y,t)}{\partial t}}\to {\frac {f(x,y,t+\Delta t)-f(x,y,t)}{\Delta t}}+{\mathcal {O}}(\Delta t^{2})$

${\frac {\partial ^{2}f(x,y,t)}{\partial x^{2}}}\to {\frac {f(x-\Delta x,y,t)-2f(x,y,t)+f(x+\Delta x,y,t)}{(\Delta x)^{2}}}+{\mathcal {O}}(\Delta x^{3})$

${\frac {\partial ^{2}f(x,y,t)}{\partial y^{2}}}\to {\frac {f(x,y-\Delta y,t)-2f(x,y,t)+f(x,y+\Delta y,t)}{(\Delta y)^{2}}}+{\mathcal {O}}(\Delta y^{3})$

Substituindo nas equações do Brusselator

${\frac {u(x,y,t+\Delta t)-u(x,y,t)}{\Delta t}}=f(u,v)+D_{u}\left({\frac {u(x-\Delta x,y,t)-2u(x,y,t)+u(x+\Delta x,y,t)}{(\Delta x)^{2}}}+{\frac {u(x,y-\Delta y,t)-2u(x,y,t)+u(x,y+\Delta y,t)}{(\Delta y)^{2}}}\right)$

${\frac {v(x,y,t+\Delta t)-v(x,y,t)}{\Delta t}}=g(u,v)+D_{v}\left({\frac {v(x-\Delta x,y,t)-2v(x,y,t)+v(x+\Delta x,y,t)}{(\Delta x)^{2}}}+{\frac {v(x,y-\Delta y,t)-2v(x,y,t)+v(x,y+\Delta y,t)}{(\Delta y)^{2}}}\right)$

onde $f(u,v)$ e $g(u,v)$ são as funções que representam a reação sem difusão.

Utilizamos discretização do tipo

$t=0,1\Delta t,2\Delta t,3\Delta t,...,t_{max}$

$x=0,1\Delta x,2\Delta x,3\Delta x,...,N_{x}$

$y=0,1\Delta y,2\Delta y,3\Delta y,...,N_{y}$

Utilizando a notação $f(i\Delta x,j\Delta y,n\Delta t)=f_{i,j}^{n}$, assumindo $\Delta x=\Delta y=\Delta s$ e rearranjando os termos, reescrevemos as equações como

$u_{i,j}^{n+1}=u_{i,j}^{n}+f(u_{i,j}^{n},v_{i,j}^{n})\Delta t+K_{u}(u_{i-1,j}^{n}+u_{i+1,j}^{n}+u_{i,j-1}^{n}+u_{i,j+1}^{n}-4u_{i,j}^{n})$

$v_{i,j}^{n+1}=v_{i,j}^{n}+g(u_{i,j}^{n},v_{i,j}^{n})\Delta t+K_{v}(v_{i-1,j}^{n}+v_{i+1,j}^{n}+v_{i,j-1}^{n}+v_{i,j+1}^{n}-4v_{i,j}^{n})$

onde $K_{u}={\frac {D_{u}\Delta t}{(\Delta s)^{2}}}$ e $K_{v}={\frac {D_{v}\Delta t}{(\Delta s)^{2}}}$.

---

Resultados

Nos gráficos foram utilizados (exceto onde for indicado outro valor)':

$N_{x}=N_{y}=50$

Onde N é o limite do "recipiente" que os reagentes se encontram.

Implementação

O método foi implementado em Python, considerando $\Delta t=0.1,\Delta s=1,N_{x}=N_{y}=50$, variando as constantes $a$ e $b$ e as condições iniciais do problema.

• Código completo no GitHub[1]

"""
Esta é uma versão reduzida do código, sem a parte da formação dos gifs e de algumas imagens.
Para a versão oficial utilizada no trabalho, acesse o GitHub forncecido.
"""

import numpy as np
import matplotlib.pyplot as plt

# Constantes
Nx = Ny = 25
a = 1
b = 1.7

# Valores iniciais
u0 = 1
v0 = 2
t = 0

# Constantes do sistema
t_max = 40
dt = 0.1
ds = 1

# Constantes dos reagentes e da estabilidade
Du = 0.1
Dv = 1
ku = Du * dt / (ds ** 2)
kv = Dv * dt / (ds ** 2)


# Pedaço da equação sem derivada parcial
def f(u, v):
    return a - (b + 1) * u + u * u * v


# Pedaço da equação sem derivada parcial
def g(u, v):
    return b * u - u * u * v


# vetores no tempo n
u_n = np.zeros((Nx, Ny))
v_n = np.zeros((Nx, Ny))

# vetores no tempo n+1
u_n1 = np.zeros((Nx, Ny))
v_n1 = np.zeros((Nx, Ny))

# Nove pontos centrais (u0)
mid = int(Nx / 2)  # Centro
mov = int(Nx / 4)  # Movendo para cima e para os lados
u_n[mid, mid] = u_n[mid + mov, mid + mov] = u_n[mid + mov, mid] = u_n[mid, mid + mov] = u_n[mid + mov, mid - mov] = u0
u_n[mid - mov, mid - mov] = u_n[mid - mov, mid] = u_n[mid, mid - mov] = u_n[mid - mov, mid + mov] = u0

# Toda a borda (v0)
for i in range(Nx):
    v_n[0, i] = v0
    v_n[i, 0] = v0
    v_n[Nx - 1, i] = v0
    v_n[i, Nx - 1] = v0

# Algumas listas são extras, não precisam realmente estar ali, estão apenas para organização.
lista_t = []
lista_u = []
lista_v = []

# Calculando concentrações com FTCS
while t < t_max:
    for i in range(Nx):
        i_e = (i - 1) % Nx  # vizinho a esquerda de 0 é o da ultima posicao
        i_d = (i + 1) % Nx  # vizinho a direita da ultima posicao é o zero

        for j in range(Ny):
            j_e = (j - 1) % Ny
            j_d = (j + 1) % Ny

            u_n1[i, j] = u_n[i, j] + dt * f(u_n[i, j], v_n[i, j]) \
                         + ku * (u_n[i_e, j] + u_n[i_d, j] + u_n[i, j_e] + u_n[i, j_d] - 4 * u_n[i, j])
            v_n1[i, j] = v_n[i, j] + dt * g(u_n[i, j], v_n[i, j]) \
                         + kv * (v_n[i_e, j] + v_n[i_d, j] + v_n[i, j_e] + v_n[i, j_d] - 4 * v_n[i, j])

    lista_u.append(u_n1[0][0])
    lista_v.append(v_n1[0][0])

    # atualizar u_n e v_n
    for i in range(Nx):
        for j in range(Ny):
            u_n[i, j] = u_n1[i, j]
            v_n[i, j] = v_n1[i, j]

    t += dt
    lista_t.append(t)

    print(f'{round(t / t_max * 100, 3)}%')

plt.plot(lista_t, lista_u, color='red', label='u(t)')
plt.plot(lista_t, lista_v, color='blue', label='v(t)')
plt.grid(True)
plt.suptitle(f'Reação-Difusão')
plt.title(f'$u_0$ = {u0} | $v_0$ = {v0} | a = {a} | b = {b}')
plt.xlabel('Tempo')
plt.ylabel('Concentrações')
plt.legend()
plt.savefig('Reação-Difusão')
plt.show()