Modelo de Gray-Scott

Descrição do Modelo

O modelo de Gray-Scott descreve uma reação autocatalítica. Sejam duas substâncias químicas cujas concentrações em um dado ponto do espaço são dadas pelas variáveis $u$ e $v$, a reação pode ser representada como

$u+2v\to 3v$

Isso significa que uma molécula da substância $u$ é transformada em uma molécula da substância $v$ por meio da ação de outras duas moléculas da substância $v$, ou seja, $v$ é um catalisador de sua própria produção (daí o termo autocatálise). Além dessa reação, ambas substâncias se difundem pelo meio (por isso esse modelo pertence à classe mais geral de modelos reativos-difusivos) e, portanto, as concentrações $u$ e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} mudam com o tempo e diferem em cada ponto. Por simplicidade, assume-se que a reação reversa (i.e., Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3v \to u + 2v} ) não ocorre.

O comportamento geral do sistema pode ser descrito pelas equações abaixo:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{\partial{u}}{\partial{t}} & = - uv^2 + F(1-u) + D_u\nabla^2u\\ \frac{\partial{v}}{\partial{t}} & = uv^2 - (F+k)v + D_v\nabla^2v \quad (1)\\ \end{align}}

A primeira das equações acima pode ser interpretada da seguinte forma. Em um dado ponto, a variação na concentração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} aumenta proporcionalmente ao laplaciano de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} naquele ponto, i.e., quando a concentração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} na vizinhança desse ponto é alta; e proporcionalmente à taxa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} de reposição de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} (taxa de alimentação, ou feed rate). A concentração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} diminui com o termo reativo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -uv^2} , que representa a reação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u + 2v \to 3v} .

De outro lado, na segunda das equações acima, a concentração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} aumenta com o termo reativo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle uv^2} e também proporcionalmente ao laplaciano de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} naquele ponto, mas diminui com a remoção de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} a uma taxa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F+k} , mais rápida, portanto, do que a reposição de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} .

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} são os parâmetros do modelo, juntamente com os coeficientes de difusão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{u}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{v}} .

O sistema pode ser imaginado como consistindo em duas substâncias Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} , envoltas por uma membrana semipermeável e imersas em um meio em que essas mesmas duas substâncias estão presentes. A membrana permite a entrada da substância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} , mas não da substância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} , e permite a saída da substância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} , mas não da substância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} .

Análise de estabilidade

Nota: A análise em toda esta seção pressupõe sempre que os parâmetros e coeficientes de difusão são positivos.

Soluções estacionárias sem difusão

O modelo de Gray-Scott depende dos parâmetros Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F, k} e dos coeficientes de difusão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{u}, D_{v}} das espécies químicas. Ignorando em um primeiro momento os termos de difusão, percebe-se que, por inspeção, o sistema possui uma solução estacionária em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}, v^{*}) = (1, 0)} para quaisquer valores dos parâmetros. Esse ponto, no entanto, não é a única solução estacionária do sistema; para encontrar as outras, é necessário impor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial u/\partial t = \partial v/\partial t = 0} nas equações do sistema. Fazendo isso e dispensando os termos de difusão (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{u} = D_{v} = 0} ), obtém-se o seguinte sistema de equações:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} - & uv^2 + F(1-u) = 0\\ & uv^2 - (F+k)v = 0 \quad (2)\\ \end{align}}

Somando essas duas equações, relacionamos as variáveis Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(1-u) - (F+k)v = 0 \Rightarrow u = 1 - \gamma v \quad (3) }

onde definiu-se o parâmetro auxiliar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = \frac{F+k}{F}} .

Substituindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} na segunda equação do sistema (2) (e reescrevendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F+k =\gamma F} ), ficamos com:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(1 - \gamma v \right)v^2 -\gamma F v = 0 \Rightarrow -\gamma v^3 + v^2 - \gamma F v = 0 \quad (4)}

Evidentemente, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = 0} é solução dessa equação, implicando em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = 1} , como já havíamos inspecionado. Alternativamente, considerando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \neq 0} , podemos dividir (4) por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} , ficando com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\gamma v^2 + v - \gamma F = 0} . Resolvendo esta equação quadrática, obtemos duas novas soluções estacionárias para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{\pm} = \frac{1}{2\gamma}(1 \pm \sqrt{1 - 4\gamma^2 F})}

Disso, pela relação (3), temos que os valores correspondentes para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} são:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{\mp} = \frac{1}{2}(1 \mp \sqrt{1 - 4\gamma^2 F})}

É necessário apontar que, para que as duas últimas soluções (não-triviais) existam — isto é, sejam números reais — o fator dentro da raiz quadrada tem de ser positivo ( Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 - 4\gamma^2 F \geq 0} ). Por consequência:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4\gamma^2 F \leq 1 \Rightarrow 4 \left(\frac{F+k}{F}\right)^2 F \leq 1 \Rightarrow F \geq 4(F+k)^2} , para que existam as soluções não-triviais.

Nesse caso, então, há três soluções estacionárias Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{i}, v^{*}_{i})} do sistema:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} & u^{*}_{0} = 1 & v^{*}_{0} & = 0 & \\ & u^{*}_{1} = \frac{1}{2}(1 + \sqrt{1 - 4\gamma^2 F}) & v^{*}_{1} & = \frac{1}{2\gamma}(1 - \sqrt{1 - 4\gamma^2 F}) &\quad (5) \\ & u^{*}_{2} = \frac{1}{2}(1 - \sqrt{1 - 4\gamma^2 F}) & v^{*}_{2} & = \frac{1}{2\gamma}(1 + \sqrt{1 - 4\gamma^2 F}) & \\ \end{align}}

Estabilidade dos estados estacionários (sem difusão)

Para avaliar a estabilidade das soluções acima, faz-se necessário obter a matriz Jacobiana dos termos de reação, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{i}(u,v)} . Explicitamente, analisando o sistema (1) de equações, temos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{1}(u,v) = -uv^2 + F(1-u)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{2}(u,v) = uv^2 - (F+k)v} . A matriz Jacobiana do sistema é então dada por:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{R}(u,v) = \begin{bmatrix}\partial_{u} R_{1}& \partial_{v} R_{1}\\ \partial_{u} R_{2}& \partial_{v} R_{2}\end{bmatrix} = \begin{bmatrix} -v^2 -F& -2uv\\ v^2 & 2uv - (F+k)\end{bmatrix} \quad (6)}

Analisemos a estabilidade para os três pares Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{i},v^{*}_{i})} de soluções estacionárias:

• Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{0},v^{*}_{0}) = (1, 0)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{R}(u^{*}_{0},v^{*}_{0}) = \begin{bmatrix}-F& 0\\ 0 & -(F+k)\end{bmatrix} \quad (7)}

Por essa ser uma matriz diagonal, os autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{i}} são justamente as entradas das diagonais; ou seja, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{1} = -F} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{2} = -(F+k)} . Uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} são parâmetros positivos, os dois autovalores são reais e negativos, e portanto o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{0},v^{*}_{0})} é sempre estável.

• Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{1,2},v^{*}_{1,2}) = \left(\frac{1}{2}(1 \pm \sqrt{1 - 4\gamma^2 F}), \frac{1}{2\gamma}(1 \mp \sqrt{1 - 4\gamma^2 F})\right)} , podemos utilizar uma estratégia que simplifica as contas. Em particular, nota-se que os dois pontos obedecem à segunda equação do sistema (2) com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \neq 0} . Desse modo, se dividirmos tal equação por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} , percebemos que ambos os pontos obedecem a:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^{*}_{i} v^{*}_{i} - (F+k) = 0 \quad (8)}

Dessa equação, podemos calcular as entradas da segunda coluna da matriz jacobiana com facilidade:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2u^{*}_{i} v^{*}_{i} = -2(F+k)}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2u^{*}_{i} v^{*}_{i} - (F+k) = (F+k)}

Assim, a matriz jacobiana desses pontos fica:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{R}(u^{*}_{i},v^{*}_{i}) = \begin{bmatrix} -(v^{*}_{i})^2 - F & -2(F+k)\\ (v^{*}_{i})^2 & (F+k)\end{bmatrix}, \quad i = 1,2 \quad (9)}

Sabemos que o produto dos autovalores dessa matriz é igual ao seu determinante. Calculando-o, obtém-se:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{i} := \operatorname{det}\left(J_{R}(u^{*}_{i},v^{*}_{i})\right) = (F+k)\left[(v^{*}_{i})^2 -F \right] \quad (10)}

Dividindo por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(F+k)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta_{i}}{F(F+k)} = \frac{(v^{*}_{i})^2}{F} -1 = \left[\frac{1 \mp \sqrt{1-4(\gamma \sqrt{F})^2}}{2(\gamma \sqrt{F})} \right]^2 -1 = \left[\frac{1 \mp \sqrt{1-4a^2}}{2a} \right]^2 -1}

onde se definiu Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = \gamma \sqrt{F}} (observação: este é o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} definido no Gros). Nota-se que a condição de existência Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^2 \leq 1/4} para os dois pontos não-triviais é equivalente a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F \geq 4(F+k)^2} . Expandindo os termos, é possível mostrar que a expressão acima pode ser reescrita como:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta_{i}}{F(F+k)} = \frac{\sqrt{1-4a^2}}{2a^2} \left(\sqrt{1-4a^2} \mp 1\right) \quad (11)}

• Para o caso Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = 1} (sinal negativo em (11)), temos a cota superior Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-4a^2 < 1} . Portanto, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{1} < 0} para todo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} que satisfaça a condição de existência. Como o determinante é negativo, sabemos que os autovalores são reais (comentário: como as entradas da matriz são reais, se os autovalores fossem complexos, seriam também conjugados, de modo que o produto deles fosse igual ao módulo ao quadrado de qualquer um, que seria um valor positivo). Ademais, como seu produto é negativo, eles têm sinais opostos; isto é, um deles é positivo, de modo que o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{1}, v^{*}_{1})} nunca seja estável. Depreendemos desse raciocínio que o determinante da matriz jacobiana de entradas reais ser positivo é uma condição necessária para que haja estabilidade do ponto.

• Já para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = 2} (sinal positivo em (11)), temos sempre que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{2} > 0} . Para verificar a estabilidade, temos que agora calcular o traço da matriz jacobiana, pois o traço é a soma dos autovalores: se os autovalores são reais, eles têm o mesmo sinal por seu determinante ser positivo, de modo que o traço compartilhe o sinal com os dois autovalores; se os autovalores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{i}} são complexos, eles serão conjugados e o traço será Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{Tr}(J_{R}) = 2 \operatorname{Re}(\lambda_{i})} , de modo que a parte real dos autovalores tenha o mesmo sinal do traço. Assim, basta que o traço seja negativo para que o ponto seja estável, e que seja positivo para que seja instável.

No caso, temos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{Tr}(J_{R}(u^{*}_{2},v^{*}_{2})) = k - (v^{*}_{2})^2} . Esse traço é negativo quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (v^{*}_{2})^2 > k} e positivo quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (v^{*}_{2})^2 < k} ; ou seja, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{2}, v^{*}_{2})} é estável quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^{*}_{2} > \sqrt{k}} e instável quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^{*}_{2} < \sqrt{k}} (lembrando que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^{*}_{2} > 0} para todo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} ). Desse modo, pode-se caracterizar uma transição de estabilidade quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^{*}_{2} = \sqrt{k}} .

Utilizando simultaneamente as equações (3) e (8), obtemos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{F+k}{v^{*}_{2}} = u^{*}_{2} = 1 - \gamma v^{*}_{2} = 1 - \frac{F+k}{F} v^{*}_{2} \Rightarrow (F+k)\frac{F+ (v^{*}_{2})^2}{F} = v^{*}_{2}}

Substituindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^{*}_{2} = \sqrt{k}} , obteremos ao final:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (F+k)^2 = F \sqrt{k} \quad (12)}

Que é uma relação entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} que caracteriza a fronteira de estabilidade para o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{2},v^{*}_{2})} .

Estabilidade dos estados estacionários (com difusão)

Precisamos agora analisar a estabilidade dos pontos estacionários na presença de difusão, como prescreve o sistema de equações (1), que descreve o modelo. Para isso, é necessário levar em consideração, para cada um dos estados de equilíbrio, os autovalores da matriz Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(J_{R} - D \omega^2\right)\Bigg|_{(u^{*}_{i}, v^{*}_{i})}} , em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} é a matriz diagonal cujas entradas são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{u}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{v}} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = \begin{bmatrix} D_{u} & 0 \\ 0 & D_{v} \end{bmatrix}}

Se escrevermos, genericamente, que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{R}(u^{*}_{i}, v^{*}_{i}) = \begin{bmatrix} a & b \\ c & d \end{bmatrix}} , teremos a seguinte matriz jacobiana de reação-difusão:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(J_{R} - D \omega^2\right)\Bigg|_{(u^{*}_{i}, v^{*}_{i})} = \begin{bmatrix} a - D_{u}\omega^2 & b \\ c & d - D_{v}\omega^2 \end{bmatrix}}

Como já detalhado acima, para que o ponto seja estável, tal matriz tem que ter a parte real de todos os seus autovalores negativa, de modo que seu determinante seja positivo (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{det}\left(J_{R} - D \omega^2\right) > 0} ) e seu traço negativo (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{Tr}\left(J_{R} - D \omega^2\right) < 0} ). Impondo tais condições à matriz acima, obteremos, após manipulações:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} a D_{v}\omega^2 + d D_{u}\omega^2 - D_{u} D_{v}\omega^4 & < \operatorname{det}(J_{R}) & \quad (13)\\ D_{u}\omega^2 + D_{v}\omega^2 & > \operatorname{Tr}(J_{R}) & \quad(14)\\ \end{align}}

Se o traço é negativo, vemos que a segunda equação é imediatamente satisfeita, pois o lado esquerdo é positivo em qualquer situação. Investiguemos, agora, se os estados estacionários que eram estáveis condicional ou incondicionalmente, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{0},v^{*}_{0})} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{2},v^{*}_{2})} , permanecem estáveis após a introdução da difusão.

• Para o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{0},v^{*}_{0})} , utilizamos a matriz (7), obtendo as seguintes desigualdades:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} -FD_{v}\omega^2 -(F+k) D_{u}\omega^2 - D_{u} D_{v}\omega^4 & < F(F+k)\\ D_{u}\omega^2 + D_{v}\omega^2 & > -2F-k \\ \end{align}}

Que são, evidentemente, satisfeitas, por análise simples de sinais de cada lado. Portanto, conclui-se que o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{0},v^{*}_{0})} é sempre estável, inclusive na presença de difusão.

Esse é um resultado, à primeira vista, surpreendente. Em geral, o surgimento de padrões complexos e não homogêneos em sistemas reativos-difusivos está relacionado à desestabilização de um ou mais estados de equilíbrio homogêneo causada pela introdução dos coeficientes de difusão (conhecida como instabilidade de Turing). Entretanto, no caso do modelo de Gray-Scott, o surgimento de padrões complexos e não homogêneos não decorre da instabilidade de Turing, uma vez que o surgimento de padrões não-triviais neste modelo ocorre mesmo quando apenas o estado de equilíbrio trivial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u^{*}_{0}, v^{*}_{0}) = (1, 0)} existir.

Implementação

O método usado para integrar as equações diferenciais parciais do modelo foi o FTCS (Foward Time Central Space). Como existem explicações do método em toda literatura e em outras entradas da Wiki (ver, por exemplo, Modelo de Turing), a explicação aqui será sucinta.

O método consiste em discretizar a derivada parcial em relação ao tempo para frente e discretizar as derivadas parciais de segunda ordem em relação ao espaço centralmente (isto é, levando em consideração os pontos adjacentes ao ponto em que ela é calculada). Para uma função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,y,t)} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f}{\partial t} \approx \frac{f(x, y, t + \Delta t) - f(x, y, t)}{\Delta t}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 f}{\partial x^2} \approx \frac{f(x + \Delta x, y, t) - 2f(x, y, t) + f(x - \Delta x, y, t)}{\Delta x^2}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 f}{\partial y^2} \approx \frac{f(x, y + \Delta y,t) - 2f(x,y,t) + f(x, y - \Delta y,t)}{\Delta y^2}}

Das duas últimas equações acima, é fácil mostrar que o laplaciano em duas dimensões, presente nas equações do sistema (1) deste trabalho, pode ser escrito como

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^2 f(x,y,t) \approx \frac{f(x + \Delta x, y, t) - 2f(x, y, t) + f(x - \Delta x, y, t)}{\Delta x^2} + \frac{f(x, y + \Delta y, t) - 2f(x, y, t) + f(x, y - \Delta y, t)}{\Delta y^2}}

Utilizando passos de mesmo tamanho nas direções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , ou seja, fazendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x = \Delta y = \Delta h} , pode-se simplificar a discretização do laplaciano para

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^2 f(x,y,t) \approx \frac{1}{\Delta h^2} \left[f(x + \Delta h, y, t) + f(x - \Delta h, y, t) + f(x, y + \Delta h,t) + f(x, y - \Delta h,t) - 4f(x, y, t) \right]}

Usando a notação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_{i}, y_{j}, t_{n}) \equiv f^{n}_{i, j}} e definindo as separações de pontos como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{n+1} = t_{n} + \Delta t} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{i+1} = x_{i} + \Delta h} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{j+1} = y_{j} + \Delta h} , fica possível então escrever as equações do modelo de forma discretizada:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} u_{i,j}^{n+1} = u_{i,j}^{n} & + \left[ -u_{i,j}^{n}(v_{i,j}^{n})^{2} + F(1-u_{i,j}^{n}) + D_u\frac{u_{i+1,j}^{n} + u_{i-1,j}^{n} + u_{i,j+1}^{n} + u_{i,j-1}^{n} - 4u_{i,j}^{n}}{\Delta h^2}\right]\Delta t\\ v_{i,j}^{n+1} = v_{i,j}^{n} & + \left[ u_{i,j}^{n}(v_{i,j}^{n})^{2} - (F+k)v_{i,j}^{n} + D_v\frac{v_{i+1,j}^{n} + v_{i-1,j}^{n} + v_{i,j+1}^{n} + v_{i,j-1}^{n} - 4v_{i,j}^{n}}{\Delta h^2}\right]\Delta t\\ \end{align}}

Utilizou-se uma rede quadrada de tamanho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 69 \times 69} . O estado inicial do sistema é aquele em que todos os pontos estão no estado de equilíbrio estável trivial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u, v) = (1, 0)} , exceto o ponto central, em que é introduzida uma perturbação com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u, v) = (0, 1)} . Foram usadas condições de fronteira conforme a Figura 1.

Figura 1 - Grid para exemplificar as condições de fronteira usadas na simulação.

Cada elemento na matriz tem quatro vizinhos, denominados por U (Up), D (Down), L (Left), R (Right). Na Figura 1, o elemento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} , possui os vizinhos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=D=5} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=L=6} ; o elemento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2} possui como vizinhos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=1} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=L=9} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=10} ; o elemento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3} tem vizinhos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=D=7} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=8} ; e, finalmente, os vizinhos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4} são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=3} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=12} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=11} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=2} .

Essas condições de fronteira e a condição inicial explicada acima buscam reproduzir as mesmas condições usadas na simulação de Sayama.

Resultados e discussão

As simulações abaixo reproduzem algumas condições simuladas por Sayama.

Simulações do Modelo de Gray-Scott para a concentração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} , com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (D_u, D_v) = (2\times10^{-5}, 10^{-5})} . A concentração é maior nas áreas mais claras.

Concentração de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (F, k) = (0.015, 0.055)} , de t=0 até t=2000.

Concentração de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (F, k) = (0.02, 0.05)} , de t=0 até t=2000.

Simulações do Modelo de Gray-Scott para a concentração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} , com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (D_u, D_v) = (2\times10^{-5}, 10^{-5})} . Nos dois casos abaixo, a concentração é menor nas áreas mais claras.

Concentração de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (F, k) = (0.030, 0.055)} , de t=0 até t=2000.

Concentração de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (F, k) = (0.030, 0.060)} , de t=0 até t=2000.

Em geral, todas as simulações apresentaram boa concordância qualitativa com os padrões simulados por Sayama; entretanto, as imagens não são isomorficamente equivalentes. Seguem abaixo alguns outros exemplos de simulações:

Figura 2. Exemplos de outras simulações realizadas para outros valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} .

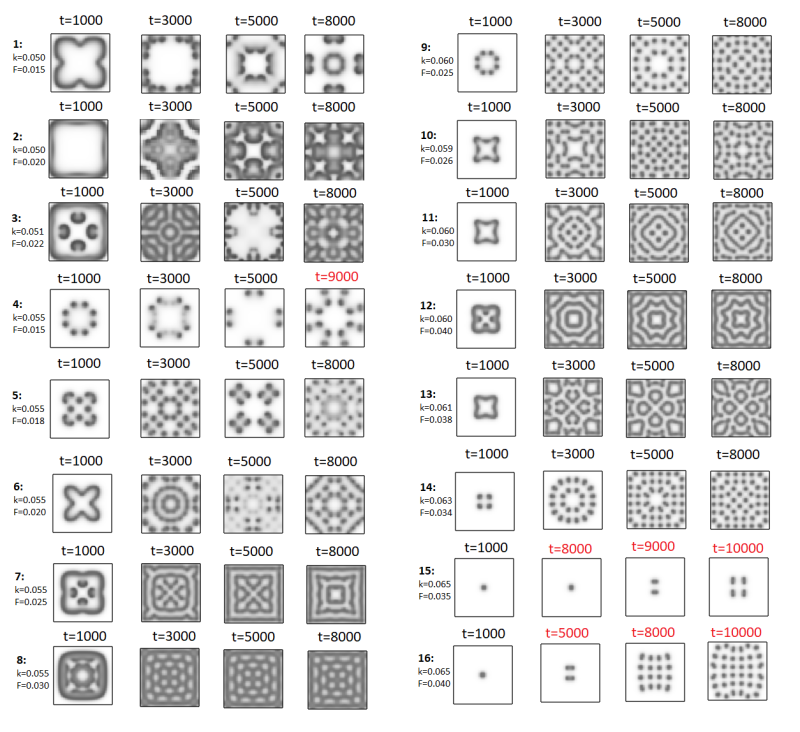
Uma explicação possível para as discrepâncias observadas é o tamanho do grid utilizado e a aplicação das condições iniciais. Possivelmente, Sayama usou um grid de tamanho par, como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100 \times 100} , por exemplo, e escolheu dois ou quatro pontos no centro da matriz como condição inicial. Como se trata da simulação de um sistema não linear, os resultados são muito sensíveis às condições iniciais. Além disso, observamos uma forte dependência dos padrões formados em relação à resolução espacial, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta h} .

Segue abaixo uma amostragem de algumas simulações realizadas e suas posições no diagrama de fases do modelo:

Figura 3. Diagrama de fases do modelo de Gray-Scott. Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} está no eixo das ordenadas, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} no eixo das abcissas. Ver [1]. A linha sólida é a curva Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=4(F+k)^{2}} .

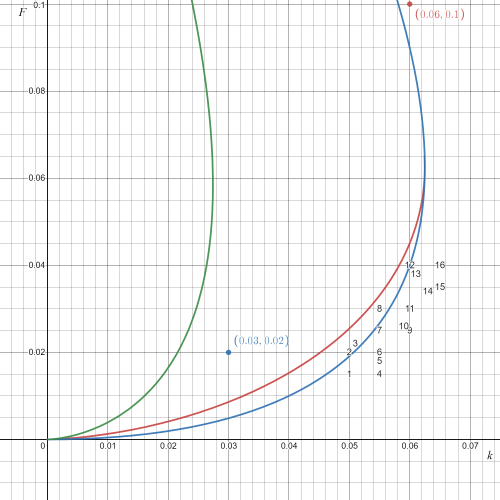
Na Figura 3 é possível observar que a grande maioria das condições que geram padrões complexos está na vizinhança da curva Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=4(F+k)^{2}} , próximo à saliência, no intervalo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.07<k<0.04} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.015<F<0.06} . Os pontos testados são os seguintes (não incluindo os pontos em azul e vermelho que já estão discriminados no gráfico):

(k,F) = {(0.050, 0.015), (0.050, 0.020), (0.051, 0.022), (0.055, 0.015), (0.055, 0.018), (0.055, 0.020), (0.055, 0.025), (0.055, 0.015), (0.060, 0.025), (0.059, 0.026), (0.0594, 0.046), (0.060, 0.030), (0.060, 0.040), (0.061, 0.038), (0.062, 0.061), (0.063, 0.054), (0.065, 0.035), (0.065, 0.040), (0.067, 0.046)}

Nota-se que, de fato, muitos padrões são gerados com a condição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F>4(F+k)^{2}} , ou seja, na região onde o único estado de equilíbrio é o estado trivial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u, v) = (1, 0)} . Como esse estado é sempre estável (ver [2]), independentemente dos valores dos coeficientes de difusão, a instabilidade de Turing não explica a formação de padrões no modelo de Gray-Scott.

Ainda em relação à Figura 3, o ponto em vermelho (classificado como "R" por Pearson - INCLUIR REFERÊNCIA), com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (k, F) = (0.06, 0.1)} , é um exemplo em que a taxa de alimentação de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} é muito grande em relação à taxa de eliminação (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F+k} ) de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} , de modo que o sistema rapidamente atinge o equilíbrio trivial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u, v) = (1, 0)} em todos os pontos. De outro lado, o ponto em azul (classificado como "B" por Pearson - INCLUIR REFERÊNCIA), com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (k, F) = (0.03, 0.02)} , é um exemplo contrário, em que a taxa de eliminação (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F+k} ) de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} é muito grande em relação à taxa de alimentação de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} , de modo que, para tempos longos, também não há formação de padrões, mas o estado que se atinge é tal que a concentração de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} é próxima de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} .

O modelo de Gray-Scott é reconhecido por exibir grande riqueza de padrões. Esses padrões foram originalmente classificados por Pearson. Uma classificação aprimorada, mais recente, pode ser encontrada nas referências. A classificação, de acordo com letras do alfabeto grego (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} , etc), leva em consideração a dinâmica e a formação de padrões complexos estáveis ou não para tempos longos, em que os sistemas, para dadas condições, atingem uma espécie de equilíbrio. Alguns dos padrões formados são linhas (stripes), manchas, pontos, padrões hexagonais. Essas formas estão em constante transformação por um período, interagindo umas com as outras, dividindo-se, mesclando-se. Eventualmente, dependendo das condições, alguns sistemas atingem um padrão estável; outros nunca se estabilizam. Alguns são mais lentos, outros mais rápidos. Por exemplo, padrões do tipo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} levam muito tempo para se formar (não conseguimos observar padrões desse tipo). Outros sistemas dependem muito mais do que outros do tamanho do grid e das condições iniciais (por exemplo, sistemas do tipo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} , que também não conseguimos observar).

No geral, a simulação conseguiu reproduzir o comportamento qualitativo de todos os pontos mostrados no espaço de fases da Figura 3, o que é um resultado notável para um método tão simples como o FCTS, com um grid pequeno e tempo/recurso computacional limitados.

Programa

Simulação do Modelo de Gray-Scott

Bibliografia

• C. Gros, "Complex and Adaptive Dynamical Systems". Springer-Verlag, Berlim, 2015.
• H. Sayama, "Introduction to the Modeling and Analysis of Complex Systems". Open SUNY Textbooks, Geneseo, NY, 2015.