Algoritmo de Wang-Landau: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 3: | Linha 3: | ||
Ao contrário dos métodos convencionais de Monte Carlo, que geram diretamente uma distribuição canônica <math>g(E) e^{-E/k_B T}</math> a uma dada temperatura <math>T</math>, a abordagem de Wang-Landau estima a densidade de estados <math>g(E)</math> diretamente por meio de um passeio aleatório, que produz um histograma plano no espaço de energia <math>H(E)</math>. | Ao contrário dos métodos convencionais de Monte Carlo, que geram diretamente uma distribuição canônica <math>g(E) e^{-E/k_B T}</math> a uma dada temperatura <math>T</math>, a abordagem de Wang-Landau estima a densidade de estados <math>g(E)</math> diretamente por meio de um passeio aleatório, que produz um histograma plano no espaço de energia <math>H(E)</math>. | ||
== | ==Amostragem de Wang-Landau== | ||
No início da simulação, <math>g(E)</math> é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir <math>g(E) = 1</math> para todas as energias possíveis <math>E</math>. A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando aleatoriamente seu estado. | No início da simulação, <math>g(E)</math> é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir <math>g(E) = 1</math> para todas as energias possíveis <math>E</math>. A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando aleatoriamente seu estado. | ||
| Linha 21: | Linha 21: | ||
onde <math>1 / g (E1)</math> é a probabilidade na energia <math>E_1</math> e <math>p (E_1\rightarrow E_2)</math> é a probabilidade de transição de <math>E_1</math> para <math>E_2</math>. | onde <math>1 / g (E1)</math> é a probabilidade na energia <math>E_1</math> e <math>p (E_1\rightarrow E_2)</math> é a probabilidade de transição de <math>E_1</math> para <math>E_2</math>. | ||
====Algoritmo==== | |||
Resumindo, o passo a passo do algoritmo pode ser escrito como: | |||
1. Seto <math>g(E) = 1</math> e um fator de modificação <math>f=e</math>; | |||
2. Aleatoriamente, flipo um spin com probabilidade <math> p(E_1 \to E_2) = min(g(E_1)/g(E_2), 1) </math>; | |||
3. Modifico a densidade de estados <math> g(E) \to g(E) \times f </math> e atualizo o histograma <math>H(E)</math>; | |||
4. Continuo até o histograma estar reto, então diminuo o valor de <math>f</math> e reseto o valor de <math>H(E)</math>; | |||
5. Repito 2-4 até <math> \ln f \approx 1 </math>. | |||
==Aplicação ao Modelo de Ising 2D== | ==Aplicação ao Modelo de Ising 2D== | ||
====Modelo de Ising==== | ====Modelo de Ising==== | ||
Uma rede 2D que consiste de uma variável discreta em cada sítio que pode ser usada para representar o momento de dipolo magnético de um átomo. | |||
Cada sítio pode ter o valor de spin <math>+1</math> ou <math>-1</math>. | |||
O hamiltoniano pode ser calculado por | |||
<math> \mathcal{H} = -J \sum_{\langle ij \rangle}\sigma_i \sigma_j </math> | |||
A soma ocorre sobre todos sítios vizinhos e a interação é ferromagnética para <math>J>0</math> e antiferromagnética para <math>J<0</math>. | |||
====Implementação==== | ====Implementação==== | ||
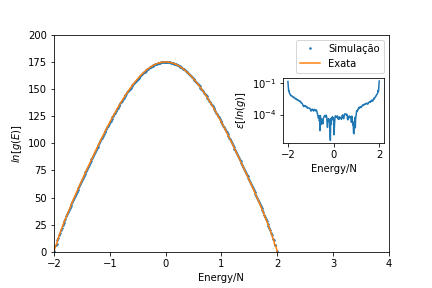
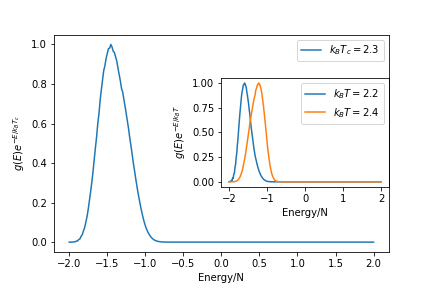
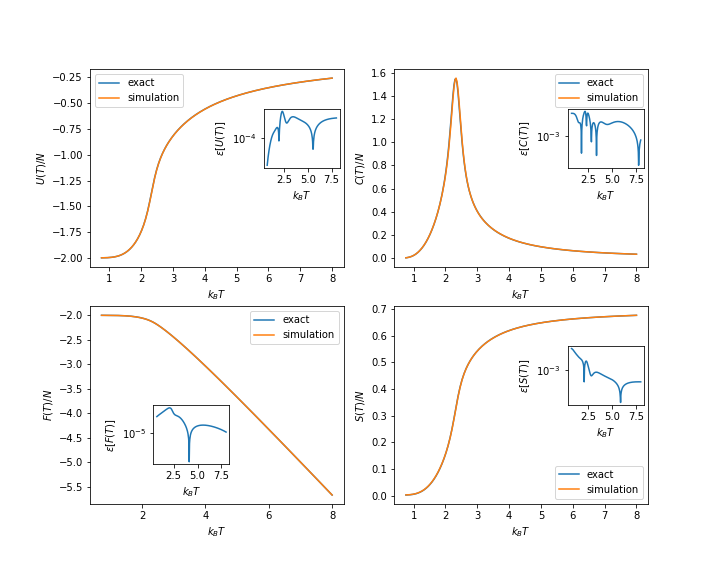
====Resultados==== | ====Resultados==== | ||
Edição das 14h44min de 28 de novembro de 2021
Introdução
Ao contrário dos métodos convencionais de Monte Carlo, que geram diretamente uma distribuição canônica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(E) e^{-E/k_B T}} a uma dada temperatura , a abordagem de Wang-Landau estima a densidade de estados diretamente por meio de um passeio aleatório, que produz um histograma plano no espaço de energia .
Amostragem de Wang-Landau
No início da simulação, é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir para todas as energias possíveis . A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando aleatoriamente seu estado.
Cada vez que uma energia Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} é visitada, a entrada correspondente em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(E)} é incrementada em 1. A estimativa de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(E)} é então modificada por um fator multiplicativo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} , e o valor atualizado realiza um passeio aleatório adicional no espaço de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} .
Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} são energias antes e depois de um valor de spin ser alterado, a probabilidade de transição da energia Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} é
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(E_1 \rightarrow E_2) = min \left( \frac{g(E_1)}{g(E_2)}, 1\right).}
A razão das probabilidades de transição de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} e de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} podem ser calculados como
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{p(E_1 \rightarrow E_2)}{p(E_2 \rightarrow E_1)} = \frac{g(E_1)}{g(E_2)}.}
Logo, o algoritmo de passeio aleatório satisfaz o equilíbrio detalhado:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{g(E_1)}p(E_1 \rightarrow E_2) = \frac{1}{g(E_2)}p(E_2 \rightarrow E_1),}
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 / g (E1)} é a probabilidade na energia Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p (E_1\rightarrow E_2)} é a probabilidade de transição de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} .
Algoritmo
Resumindo, o passo a passo do algoritmo pode ser escrito como:
1. Seto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(E) = 1} e um fator de modificação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=e} ;
2. Aleatoriamente, flipo um spin com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(E_1 \to E_2) = min(g(E_1)/g(E_2), 1) } ;
3. Modifico a densidade de estados Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(E) \to g(E) \times f } e atualizo o histograma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(E)} ;
4. Continuo até o histograma estar reto, então diminuo o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} e reseto o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(E)} ;
5. Repito 2-4 até Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln f \approx 1 } .
Aplicação ao Modelo de Ising 2D
Modelo de Ising
Uma rede 2D que consiste de uma variável discreta em cada sítio que pode ser usada para representar o momento de dipolo magnético de um átomo.
Cada sítio pode ter o valor de spin Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle +1} ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1} .
O hamiltoniano pode ser calculado por
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = -J \sum_{\langle ij \rangle}\sigma_i \sigma_j }
A soma ocorre sobre todos sítios vizinhos e a interação é ferromagnética para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J>0} e antiferromagnética para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J<0} .