Equação de Cahn-Hilliard

Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David e Guilherme Hoss

O objetivo deste trabalho é resolver computacionalmente a equação de Cahn-Hilliard, que descreve o processo de decomposição espinodal de uma mistura binária, utilizando o método FTCS (Forward Time Centered Space).

Decomposição Espinodal

Decomposição espinodal é o nome dado ao processo no qual uma pequena perturbação de um sistema faz com que, uma fase homogênea termodinamicamente instável, diminua sua energia e separe-se espontaneamente em duas outras fases coexistentes, esse é um processo que ocorre sem nucleação, ou seja, é instantâneo. Ela é observada, por exemplo, em misturas de metais ou polímeros e pode ser modelada pela equação de Cahn-Hilliard.

A Equação de Cahn-Hilliard

A equação de Cahn-Hilliard descreve o processo de decomposição espinodal de uma mistura binária. Em outras palavras, é uma equação que descreve o processo de separação de fase entre dois componentes de um fluido binário que se separam de maneira espontânea.

Consideraremos - de início - uma mistura binária de dois componentes A e B descritas pelas concentrações dos fluidos $c_{a}(x,t)$ e $c_{b}(x,t)$, respectivamente.

Além disso, podemos considerar que - para uma mistura binária - $c_{a}(x,t)+c_{b}(x,t)=1$ e portanto podemos simplificar para apenas uma concentração $c(x,t)$:

$c_{a}(x,t)=c(x,t),c_{b}(x,t)=1-c(x,t)$

Tendo isso em vista, podemos agora utilizar a primeira lei de Fick da difusão:

$J=-D\nabla c$

juntamente da equação da continuidade:

${\frac {\partial c}{\partial t}}+\nabla \cdot {\vec {J}}=0$

Onde $D$ é o coeficiente de difusão e ${\vec {J}}$ é o fluxo de difusão. Em seguida, ao combinarmos ambas as equações anteriores o resultado gera a segunda lei de Fick da difusão:

${\frac {\partial c}{\partial t}}=D{\nabla }^{2}c$

Por definição, verificou-se que a concentração não poderia ser a razão da difusão, portanto outra força estaria presente. E, nesse caso, encontrou-se que a principal força responsável pela difusão negativa é o potencial químico. Portanto, outra equação pode ser derivada para generalizar a primeira lei de Fick:

$J=-M\nabla \mu$

Onde $M$ é a mobilidade das partículas (análoga à D) e $\mu$ é o potencial químico. Com essa nova equação podemos agora também deduzir uma nova equação para a segunda lei de Fick:

${\frac {\partial c}{\partial t}}=M{\nabla }^{2}\mu$

Essa equação também é conhecida como equação de Cahn-Hilliard.

Nessa equação, podemos usar a definição do potencial químico através da densidade da energia livre de Gibbs como:

$\mu ={\frac {\partial g}{\partial c}}$

Onde $g$ é a densidade da energia livre de Gibbs e $c$ é a concentração.

Tendo em vista a substituição do termo $\mu$ por um termo que envolva a concentração dos fluidos, utiliza-se uma equação que descreve a densidade de energia desse sistema através da concentração dos mesmos:

$G=\int _{V}^{}f(c)+{\kappa |\nabla c|}^{2}dV$

Nesse caso, $G$ é a energia livre de Gibbs, $f(c)$ é a densidade de energia livre devido à contribuições de ambas as fases homogêneas e ${\kappa |\nabla c|}^{2}$ é a densidade de energia livre devido ao gradiente de concentração na interface (ou energia de interface).

Além disso, a função $f(c)$ tem o formato de um poço de potencial duplo, que pode ser representado pela seguinte equação:

$f(c)={\frac {(c^{2}-1)^{2}}{4}}$

Levando essas informações em conta e - utilizando um parâmetro $\gamma$ análogo à largura da interface - que é descrito por $\kappa =\gamma ^{2}$ é possível encontrar uma equação que descreve a densidade de energia livre de Gibbs para um sistema duplo-fásico:

$g(c)=f(c)+{\gamma }^{2}{|\nabla c|}^{2}$

Com essas igualdades agora se torna possível o cálculo de $\mu$ em função da concentração dos fluidos:

$\mu ={\frac {\partial g}{\partial c}}={\frac {\partial f(c)}{\partial c}}+{\frac {\partial {(\gamma }^{2}{|\nabla c|}^{2})}{\partial c}}={\frac {\partial ({\frac {(c^{2}-1)^{2}}{4}})}{\partial c}}+{\gamma }^{2}{\nabla }^{2}c=c^{3}-c+{\gamma }^{2}{\nabla }^{2}c$

Finalmente - utilizando a última expressão encontrada - torna-se possível reescrever o potencial químico em função da mobilidade de suas partículas ($M$) e a concentração do fluido:

${\frac {\partial c}{\partial t}}=M{\nabla }^{2}(c^{3}-c-\gamma {\nabla }^{2}c)$

Essa equação final é chamada de equação de Cahn-Hilliard. A equação dependente da difusão é análoga e também funcional:

${\frac {\partial c}{\partial t}}=D{\nabla }^{2}(c^{3}-c-\gamma {\nabla }^{2}c)$

Método FTCS (Forward Time Centered Space)

O FTCS é um método numérico utilizado para resolver equações diferenciais parciais, tais como a difusão do calor e do transporte de massa, traduzindo, significa "Progressivo no tempo, avançado no espaço". Uma das formas que o método pode ser utilizado é a forma explícita que está descritas abaixo.

$n\to \Delta t$

$j\to \Delta x$

FTCS Explicito

${\frac {\partial f}{\partial t}}\to {\frac {f_{j}^{n+1}-f_{j}^{n}}{\Delta t}}$

${\frac {\partial ^{2}f}{\partial x^{2}}}\to {\frac {f_{j-1}^{n}-2f_{j}^{n}+f_{j+1}^{n}}{\Delta x^{2}}}$

Para difusão:

$f_{j}^{n+1}=f_{j}^{n}+{\frac {D\Delta t}{(\Delta x)^{2}}}(f_{j-1}^{n}-2f_{j}^{n}+f_{j+1}^{n})$

Resolução da equação de Cahn-Hilliard para FTCS explicito somente para x:

$\displaystyle {\frac {\partial c}{\partial t}}=D\nabla ^{2}(c^{3}-c-\gamma ^{2}\nabla ^{2}c)$

$\displaystyle {\frac {c_{j}^{n+1}-c_{j}^{n}}{\Delta t}}=D\displaystyle {\frac {\partial ^{2}}{\partial x^{2}}}(c^{3}-c-\gamma ^{2}\displaystyle {\frac {\partial ^{2}c}{\partial x^{2}}})$

$\displaystyle {\frac {c_{j}^{n+1}-c_{j}^{n}}{\Delta t}}=D{\frac {u_{j-1}^{n}-2u_{j}^{n}+u_{j+1}^{n}}{(\Delta x)^{2}}}$

$\displaystyle {\frac {c_{j}^{n+1}-c_{j}^{n}}{\Delta t}}=D\left({\frac {(c_{j-1}^{n})^{3}-2(c_{j}^{n})^{3}+(c_{j+1}^{n})^{3}}{(\Delta x)^{2}}}-{\frac {c_{j-1}^{n}-2c_{i}^{n}+c_{j+1}^{n}}{(\Delta x)^{2}}}-\gamma ^{2}{\frac {c_{j-2}^{n}-4c_{j-1}^{n}+6c_{j}^{n}-4c_{j+1}^{n}+c_{j+2}^{n}}{(\Delta x)^{4}}}\right)$

$c_{j}^{n+1}=D\Delta t\left({\frac {(c_{j-1}^{n})^{3}-2(c_{i}^{n})^{3}+(c_{j+1}^{n})^{3}}{(\Delta x)^{2}}}-{\frac {c_{j-1}^{n}-2c_{j}^{n}+c_{j+1}^{n}}{(\Delta x)^{2}}}-\gamma ^{2}{\frac {c_{j-2}^{n}-4c_{j-1}^{n}+6c_{j}^{n}-4c_{j+1}^{n}+c_{j+2}^{n}}{(\Delta x)^{4}}}\right)+c_{j}^{n}$

$c_{j}^{n+1}={\frac {D\Delta t}{(\Delta x)^{2}}}\left((c_{j-1}^{n})^{3}-2(c_{i}^{n})^{3}+(c_{j+1}^{n})^{3}-{c_{j-1}^{n}+2c_{j}^{n}-c_{j+1}^{n}}-\gamma ^{2}{\frac {c_{j-2}^{n}-4c_{j-1}^{n}+6c_{j}^{n}-4c_{j+1}^{n}+c_{j+2}^{n}}{(\Delta x)^{2}}}\right)+c_{j}^{n}$

Condição de Estabilidade

A estabilidade dessa equação mostra-se muito mais complicada de se estipular por ela ser uma equação diferencial de quarta ordem se comparada a equação de difusão, Portanto só iremos analisar a seção 3.3 (Experimental and theoretical stability conditions) do artigo Numerical methods for the implentation of the Cahn-Hilliard equation in one dimension and a dynamic boundary condition in two dimensions [1].

Após a linearização e aplicação do teorema de Gershgorin temos que a condição para estabilidade da equação linear para $D=1$ é:

$\Delta t<\displaystyle {\frac {(\Delta x)^{2}}{4+{\frac {8\gamma ^{2}}{\Delta x^{2}}}}}$

Importante atentar que essa é a condição de estabilidade somente para a equação de Cahn-Hilliard linearizada, não para a original. Tanto que a literatura sobre a equação propõem que $\Delta t$ $\varpropto$ $(\Delta x)^{4}$, que é o que acontece na condição estabilidade linear quando $\gamma >>\Delta x$.

O artigo compara os dados experimentais de estabilidade com a estabilidade da equação linearizada relacionado na seção 3.3.4 e conclui que para valores de ${\frac {\gamma }{\Delta x}}\in [0.25,8]$ a condição teórica encontrada a partir da linearização é uma boa aproximação.

Resultados

Com o intuito de testar o comportamento da equação, variou-se o coeficiente de difusão para que fossem analisados seus gráficos.

Gráfico 1: Resultados da simulação variando os coeficientes de difusão (D) para tempos máximos diferentes, $\gamma =3.4/128,\Delta t=1/500000$

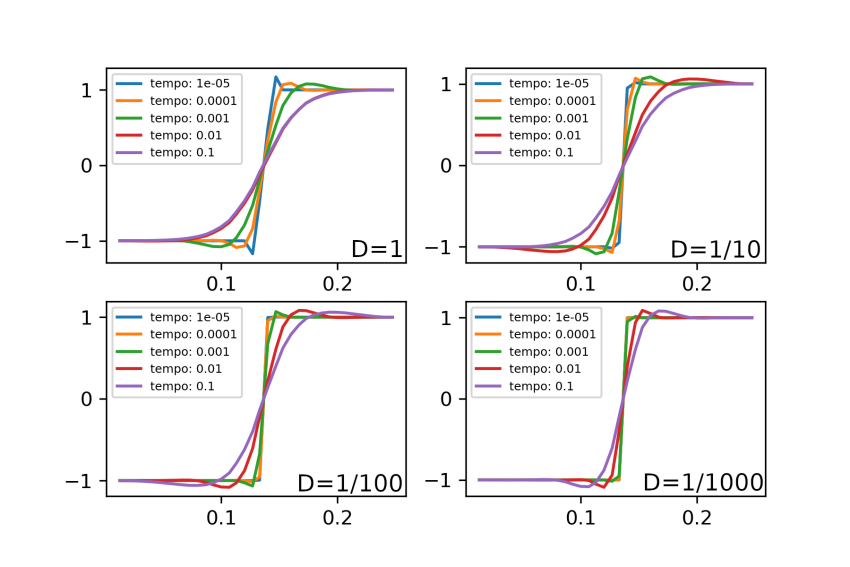
Nos gráficos, é possível observar que quanto maior o coeficiente de difusão maior é a velocidade em que a mistura atinge a estabilidade. Além disso, vemos que valores baixos de t produzem soluções mais íngremes que valores altos de t.

Discussão de Resultados

Uma propriedade observada no gráfico 1 é a de que os valores das soluções obtidas utilizando o método FTCS excedem os valores máximos e mínimos permitidos ( C=1 e C=-1), se estivesse modelando uma situação real isso iria contra a lei de conservação de massa, o que pode ocasionar erros nos resultados que exigem uma grande precisão.

Valores de D acima O método FTCS explícito, limita-se por causa da condição de estabilidade, por isso esse método não é recomendado para modelos com alto $\gamma$. Para tais modelos, o método FTCS implícito é mais recomendado por ser incondicionalmente estável.

Implementção

def vector_declaration(L,dx):
  c = [[],[]] # vetor concentração
  espaco = []
  # Condições iniciais
  for i in range(int(L/dx)+4):##+4 pois usaremos dois valores antes e depois do ultimo elemento do vetor c
    if (i<1/2*L/dx+2):
      c[0].append(-1)
      c[1].append(-1)
    else:
      c[0].append(1)
      c[1].append(1)
    espaco.append(round(i/150,3))
  return c, espaco

def CH_equation(gamma, D, dx, dt, L, TEMPO_MAX): # resolução numérica da equação

  c, espaco = vector_declaration(L, dx)
  i = 0
  for time in [t*dt/TEMPO_MAX for t in range(int(TEMPO_MAX/dt))]:
    for l in range(2,len(c[1][2:-2])):
      c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][l+1]**3
      c2 = -c[i][l-1] + 2*c[i][l] - c[i][l+1]
      c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][l+1] + c[i][l+2]
      c[1-i][l] = D*dt/(dx**2)*(c1+c2-gamma**2*c3/(dx**2)) + c[i][l]
   i = 1-i

  return(espaco[2:-2],c[1-i][2:-2]) ##retirando os elementos a mais do vetor

tempo=1
tamanho=1/3.5
Difuse= 1
gamma=3.4*1/128
dt=1/500000
dx = 1/128

figure, axis = plt.subplots(2, 2)
plt.figure(dpi=500)

axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000))
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
axis[0, 0].legend(loc="upper left", prop={'size': 6})

axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000))
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
axis[0, 1].legend(loc="upper left", prop={'size': 6})

axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000))
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
axis[1, 0].legend(loc="upper left", prop={'size': 6})


axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000))
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
axis[1, 1].legend(loc="upper left", prop={'size': 6})

plt.show()
plt.savefig('graficosDIFUSAO.png', dpi=500)

Referências

[1] SIBBING, Zimo. Numerical methods for the implentation of the Cahn-Hilliard equation in one dimension and a dynamic boundary condition in two dimensions, tese de bacharelado, 2015.

[2] MARKUS, Wilczek. The Cahn-Hilliard Equation, 2015.

[3] CAHN, John W.; HILLIARD, John E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. The Journal of Chemical Physics, 1958.

[4] https://pt.wikipedia.org/wiki/Lei_de_Fick

[5] https://en.wikipedia.org/wiki/Spinodal_decomposition

[6] https://pt.qaz.wiki/wiki/Cahn%E2%80%93Hilliard_equation