Interpolação e extrapolação

Dado um conjunto de dados $(X_{1},Y_{1}),(X_{2},Y_{2}),\cdots (X_{N},Y_{N})$, onde $\;Y_{i}$ corresponde ao valor da grandeza $\;Y$ em $\;X=X_{i}$, aproximações podem ser desenvolvidas para se obter estimativas de $\;Y(X)$, em valores de $\;X$ que não constam do conjunto. Se $X_{1}\leq X\leq X_{N}$ esta estimativa é denominada interpolação, caso contrário, chamamos de extrapolação. Usualmente, os mesmos algoritmos são usados nos dois casos.

Em geral, extrapolações são mais perigosas, uma vez que deve-se presumir o comportamento da função em regiões onde não se conhece nada sobre ela. Supõe-se que o comportamento perto da fronteira da região conhecida se estende até o ponto de interesse, o que constitui um "ato de fé". Embora seja extremamente útil para se estimar valores da grandeza além da região conhecida, cabe ressaltar que atrasos significativos no desenvolvimento de grande parte da física moderna teriam ocorrido se tivéssemos nos limitado a extrapolações ao invés de se realizar medidas pois muitos comportamentos diferentes, provenientes de um física nova, foram observados. Apesar disto, extrapolações cuidadosas constituem uma poderosa ferramenta em várias áreas, como por exemplo, na resolução numérica de equações diferencias.

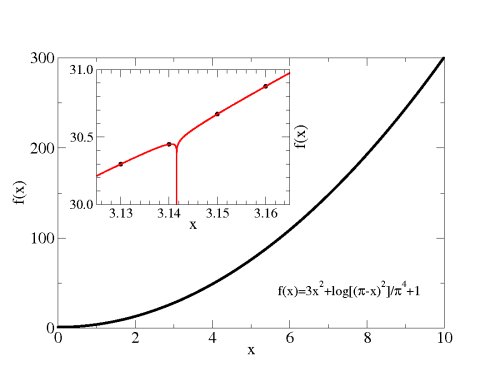
Embora a interpolação possa parecer inofensiva, dificuldades também podem ser encontradas. Um exemplo clássico, evocado no livro Numerical Recipes, é a função:

$f(x)=3x^{2}+{\frac {\log[(\pi -x)^{2}]}{\pi ^{4}}}+1$

A figura abaixo mostra valores de $f(x)$ calculados a partir desta fórmula, usando valores de $X_{i}$ igualmente espaçados em $0.01$, no intervalo $0\leq X\leq 10$. Note que, este nível de detalhe de conhecimento sobre a função é, em geral, muito satisfatório tanto em cálculos numéricos quanto em medidas experimentais. Contudo, embora a função pareça crescer monotonamente, o detalhe mostrado no interior da figura revela claramente que erros grosseiros serão cometidos por fórmulas de interpolação na região $x\approx \pi$. A curva em vermelho corresponde à fórmula acima, enquanto que os pontos representam os valores tabulados. Isto mostra que, como sempre, em se tratando de aproximações numéricas, todas as "receitas" devem sempre ser analisadas cuidadosamente em cada aplicação.

Além dos aspectos sutis levantados acima, outra regra importante a ser observada em cálculos numéricos é que polinômios de grau elevado devem ser evitados. Embora seu uso permita a imposição de várias propriedades desejadas, como a imposição da continuidade das derivadas da função, por exemplo, um polinômio de grau $\;n$ possui o mesmo número de raízes. Isto faz com que eles oscilem fortemente. Logo, isto pode levar a comportamentos indesejados em extrapolações.

No caso da interpolação, este efeito também ocorre. Ou seja, o uso de polinômios de grau elevado por causar problemas. Por construção, os valores da função são reproduzidos nos pontos $\;X_{i}$. No entanto, ainda assim podem ocorrer fortes oscilaçõesê entre 2 pontos adjacentes se a ordem do polinômio for muito elevada. Não há regras simples para se determinar, no caso geral, qual é o melhor grau a ser utilizado. Os teoremas matemáticos genéricos requerem tanta informação sobre a função que, na verdade, se as conhecessemos, não precisaríamos fazer aproximações polinomiais. Uma boa receita para se evitar dificuldades consiste em se utilizar o polinômio de ordem mais baixa possível que garanta as propriedades e precisão desejadas. No caso em que os dados em consideração são obtidos a partir de cálculos numéricos, maior precisão pode ser obtida aumentando-se o número de pontos do conjunto de dados, mantendo-se o grau do polinômio empregado. Em se tratando de dados experimentais, onde em geral pode não ser simples (até mesmo por razões de custo) se obter mais pontos intermediários, aumentar um pouco o grau do polinômio pode ser uma solução aceitável. Se ainda assim isto não for suficiente, cabe ressaltar que existem outros métodos vai além de aproximações polinomiais e que técnicas baseadas em razões entre polinômios diferentes ou envolvendo funções mais complexas podem ser utilizadas com segurança.

No link a seguir, "Interpolação polinomial e Fórmula de Lagrange", há um exemplo de interpolação / extrapolação polinomial.

Este assunto é muito vasto para ser tratado nesta abordagem introdutória. Uma discussão mais completa pode ser encontrada, por exemplo, no livro Numerical Recipes. Em particular, boa parte da discussão a seguir, sobre a Fórmula de Lagrange e Spline cúbico, é fortemente baseada na apresentação deste livro.

---

Voltar para o índice de Métodos computacionais.