Pêndulos Estocásticos: mudanças entre as edições
(Criou página com ''''Grupo :''' Gustavo H. Guesser, Joshua L. Kipper, Marcos Pasa. == Pêndulo Simples == Primeiramente vamos inserir ruído em um pêndulo simples, que é constituído de uma barra de comprimento <math>l</math>, sem massa e rígida que contém uma massa <math>m</math> pontual em sua ponta, conforme ilustrado na figura a seguir. <center> thumb|upright=2|center|Esquema de um pêndulos simples em um campo gravitacional constante. </center>...') |
|||
| Linha 2: | Linha 2: | ||
== Pêndulo Simples == | == Pêndulo Simples == | ||
===Equação de movimento=== | |||
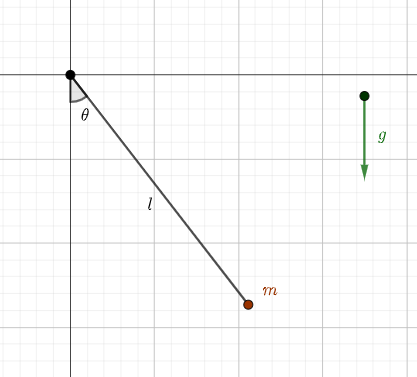
Primeiramente vamos inserir ruído em um pêndulo simples, que é constituído de uma barra de comprimento <math>l</math>, sem massa e rígida que contém uma massa <math>m</math> pontual em sua ponta, conforme ilustrado na figura a seguir. | Primeiramente vamos inserir ruído em um pêndulo simples, que é constituído de uma barra de comprimento <math>l</math>, sem massa e rígida que contém uma massa <math>m</math> pontual em sua ponta, conforme ilustrado na figura a seguir. | ||
| Linha 8: | Linha 9: | ||
</center> | </center> | ||
Considerando que a força de resistência que atua na massa é <math>- | Considerando que o pêndulo está sob o efeito da gravidade e se encontra submerso em um fluido viscoso (como o ar), tal que a força de resistência que atua na massa é <math>-2b\vec v</math>, a equação de movimento é dada por: | ||
<center> | <center> | ||
<math> | <math> | ||
\theta(t) = -\frac{2b}{m}\dot \theta - \frac{g}{l}sen(\theta) </math> | \ddot \theta(t) = -\frac{2b}{m}\dot \theta - \frac{g}{l}sen(\theta) </math> | ||
</center> | |||
Vamos supor que existe uma força ruidosa atuando em <math>m</math> (<math>F_r(t)</math>), que pode ser modelada por um ruído branco gaussiano <math>\xi(t)</math> da seguinte forma | |||
<center> | |||
<math> | |||
F_r(t) = m \alpha \xi(t) | |||
</math> | |||
</center> | |||
em que <math>\alpha</math> é a intensidade do ruído. <math>\xi(t)</math> é caracterizado pelas seguintes propriedades: | |||
<center> | |||
<math> | |||
\langle \xi(t) \rangle = 0,~~ \langle \xi(t_2)\xi(t_1) \rangle = \delta(t_2 -t_1) | |||
</math> | |||
</center> | |||
Adicionando essa nova força nas equações de movimento, ficamos com | |||
<center> | |||
<math> | |||
\ddot \theta(t) = -\frac{2b}{m}\dot \theta - \frac{g}{l}sen(\theta) + \frac{\alpha}{l}\xi(t) </math> | |||
</center> | |||
A partir de agora, por questão de simplicidade, vamos supor que <math>g = l = 1 </math>, então | |||
<center> | |||
<math> | |||
\ddot \theta(t) = -2b\dot \theta - sen(\theta) + \alpha\xi(t) </math> | |||
</center> | |||
===Método de integração=== | |||
Vamos montar um métodos para integrar o sistema no tempo. Primeiramente vamos dividir a equação em duas equações diferencias de primeira ordem, introduzindo a variável <math>\omega := \dot \theta </math>, então ficamos com o seguinte sistema | |||
<center> | |||
<math> | |||
\begin{aligned} | |||
\dot \theta &= \omega \\ | |||
\dot \omega &= -2b\dot \theta - sen(\theta) + \alpha\xi(t) | |||
\end{aligned} | |||
</math> | |||
</center> | </center> | ||
Edição das 16h29min de 18 de agosto de 2024
Grupo : Gustavo H. Guesser, Joshua L. Kipper, Marcos Pasa.
Pêndulo Simples
Equação de movimento
Primeiramente vamos inserir ruído em um pêndulo simples, que é constituído de uma barra de comprimento , sem massa e rígida que contém uma massa pontual em sua ponta, conforme ilustrado na figura a seguir.
Considerando que o pêndulo está sob o efeito da gravidade e se encontra submerso em um fluido viscoso (como o ar), tal que a força de resistência que atua na massa é , a equação de movimento é dada por:
Vamos supor que existe uma força ruidosa atuando em (), que pode ser modelada por um ruído branco gaussiano da seguinte forma
em que é a intensidade do ruído. é caracterizado pelas seguintes propriedades:
Adicionando essa nova força nas equações de movimento, ficamos com
A partir de agora, por questão de simplicidade, vamos supor que , então
Método de integração
Vamos montar um métodos para integrar o sistema no tempo. Primeiramente vamos dividir a equação em duas equações diferencias de primeira ordem, introduzindo a variável , então ficamos com o seguinte sistema