Equação de Schrödinger Unidimensional: mudanças entre as edições

Edição das 14h28min de 23 de abril de 2024

Conhecer o estado de uma partícula, na Mecânica Clássica, é saber, em um determinado momento, sua velocidade e sua posição. A partir destes valores, é possível determinar os seus futuros estados utilizando as relações fornecidas pelas Leis de Newton. Na Mecânica Quântica, porém, o estado físico não é mais caracterizado por uma quantidade discreta de valores numéricos, e sim, por uma função. A chamada Função de Onda, $\Psi$ , nos informa a evolução temporal do estado quântico de uma partícula, seguindo a Equação de Schrödinger. Em uma dimensão, a Equação de Schrödinger é dada por:

$-{\frac {\hbar }{2m}}{\frac {\partial ^{2}\Psi }{\partial x^{2}}}+V(x)\Psi =i\hbar {\frac {\partial \Psi }{\partial t}}$

O Método De Crank-Nicolson

A fim de resolvê-la numericamente para diferentes tipos de potenciais, usou-se o Método de Crank-Nicolson de resolução de EDPs. Este método baseia-se em combinar os métodos explícito e implícito (com igual contribuição) para aumentar sua estabilidade.

O método explícito FTCS (Forward Time Central Space) consiste em tomar derivadas temporais "para frente" e manter a derivada espacial centrada.

${\frac {\partial \Psi (x,t)}{\partial t}}={\frac {\Psi (x,t+\Delta t)-\Psi (x,t)}{\Delta t}}$

${\frac {\partial \Psi (x,t)}{\partial x}}={\frac {\Psi (x+\Delta x,t)-\Psi (x,t)}{\Delta x}}$ ; ${\frac {\partial ^{2}\Psi (x,t)}{\partial ^{2}x}}={\frac {(\Psi (x+\Delta x,t)-\Psi (x+\Delta x-\Delta x,t))-(\Psi (x,t)-\Psi (x-\Delta x,t))}{\Delta x\Delta x}}={\frac {\Psi (x+\Delta x,t)+\Psi (x-\Delta x,t)-2\Psi (x,t)}{\Delta x^{2}}}$

Tomando $\hbar =m=1$ (unidades atômicas), ao inserirmos as expressões acima na Equação de Schrödinger, temos que:

${\frac {i}{2}}{\frac {\Psi (x+\Delta x,t)+\Psi (x-\Delta x,t)-2\Psi (x,t)}{\Delta x^{2}}}-iV(x)\Psi (x,t)={\frac {\Psi (x,t+\Delta t)-\Psi (x,t)}{\Delta t}}$

Simplificando a notação para $\Psi (x,t)=\Psi _{j}^{n}$ , onde $j$ representa a posição e $n$ o tempo, e reorganizando os termos, ficamos com:

$\Psi _{j}^{n+1}=\Psi _{j}^{n}+{\frac {i\Delta t}{2\Delta x^{2}}}(\Psi _{j+1}^{n}+\Psi _{j-1}^{n}-2\Psi _{j}^{n})-i\Delta tV_{j}\Psi _{j}^{n}$

O método implícito é semelhante, porém a derivada temporal é "para trás".

${\frac {\partial \Psi (x,t)}{\partial t}}={\frac {\Psi (x,t)-\Psi (x,t-\Delta t)}{\Delta t}}$

O que nos leva a ter:

$\Psi _{j}^{n}=\Psi _{j}^{n-1}+{\frac {i\Delta t}{2\Delta x^{2}}}(\Psi _{j+1}^{n}+\Psi _{j-1}^{n}-2\Psi _{j}^{n})-i\Delta tV_{j}\Psi _{j}^{n}$

que, com uma substituição de variável (que é muda), nos dá, enfim:

$\Psi _{j}^{n+1}=\Psi _{j}^{n}+{\frac {i\Delta t}{2\Delta x^{2}}}(\Psi _{j+1}^{n+1}+\Psi _{j-1}^{n+1}-2\Psi _{j}^{n+1})-i\Delta tV_{j}\Psi _{j}^{n+1}$

Como dito, o Método de Crank-Nicolson é uma combinação dos métodos implícito e explícito, cada um tendo o mesmo peso de 1/2. Ao somarmos as duas equações (cada uma multiplicada por 0.5), ficaremos com a seguinte expressão:

$\Psi _{j}^{n+1}=\Psi _{j}^{n}+{\frac {i\Delta t}{4\Delta x^{2}}}(\Psi _{j+1}^{n}+\Psi _{j-1}^{n}-2\Psi _{j}^{n}+\Psi _{j+1}^{n+1}+\Psi _{j-1}^{n+1}-2\Psi _{j}^{n+1})-{\frac {i\Delta t}{2}}V_{j}(\Psi _{j}^{n}+\Psi _{j}^{n+1})$

que, ao reorganizarmos para isolar os $\Psi _{j}^{n+1}$ , resulta em:

 $\left(1+{\frac {i\Delta t}{2\Delta x^{2}}}+{\frac {i\Delta t}{2}}V_{j}\right)\Psi _{j}^{n+1}-{\frac {i\Delta t}{4\Delta x^{2}}}\Psi _{j+1}^{n+1}-{\frac {i\Delta t}{4\Delta x^{2}}}\Psi _{j-1}^{n+1}=\left(1-{\frac {i\Delta t}{2\Delta x^{2}}}-{\frac {i\Delta t}{2}}V_{j}\right)\Psi _{j}^{n}+{\frac {i\Delta t}{4\Delta x^{2}}}\Psi _{j+1}^{n}+{\frac {i\Delta t}{4\Delta x^{2}}}\Psi _{j-1}^{n}$

Para resolver a equação em simultaneamente para ambos os tempos e em todos os pontos, escrevemos a equação em forma matricial:

{\begin{pmatrix}1+2b+{\frac {i\Delta tV_{j}}{2}}&-b&0&\cdots &0&0&0\\-b&1+2b+{\frac {i\Delta tV_{j}}{2}}&-b&0&\cdots &0&0\\\vdots &\vdots &\ddots &\ddots &\ddots &\vdots &\vdots \\0&0&0&\cdots &0&-b&1+2b+{\frac {i\Delta tV_{j}}{2}}\end{pmatrix}}{\begin{pmatrix}\Psi _{1}^{n+1}\\\Psi _{2}^{n+1}\\\vdots \\\Psi _{j}^{n+1}\end{pmatrix}}={\begin{pmatrix}1-2b-{\frac {i\Delta tV_{j}}{2}}&+b&0&\cdots &0&0&0\\+b&1-2b-{\frac {i\Delta tV_{j}}{2}}&+b&0&\cdots &0&0\\\vdots &\vdots &\ddots &\ddots &\ddots &\vdots &\vdots \\0&0&0&\cdots &0&+b&1-2b-{\frac {i\Delta tV_{j}}{2}}\end{pmatrix}}{\begin{pmatrix}\Psi _{1}^{n}\\\Psi _{2}^{n}\\\vdots \\\Psi _{j}^{n}\end{pmatrix}};

com $b={\frac {i\Delta t}{4\Delta x^{2}}}$ .

Podemos notar que a diferença entre as matrizes que multiplicam $\Psi _{j}^{n+1}$ e $\Psi _{j}^{n}$ é somente o sinal das componente imaginárias. Assim, a equação final pode ser escrita como:

 $A\Psi _{j}^{n+1}=A^{*}\Psi _{j}^{n}$ , onde A é a matriz  ${\begin{pmatrix}1+2b+{\frac {i\Delta tV_{j}}{2}}&-b&0&\cdots &0&0&0\\-b&1+2b+{\frac {i\Delta tV_{j}}{2}}&-b&0&\cdots &0&0\\\vdots &\vdots &\ddots &\ddots &\ddots &\vdots &\vdots \\0&0&0&\cdots &0&-b&1+2b+{\frac {i\Delta tV_{j}}{2}}\end{pmatrix}}$

Estabilidade do Método de Crank-Nicolson

Para verificar a estabilidade, devemos primeiro olhar para a equação que define o método:

 $\left(1+{\frac {i\Delta t}{2\Delta x^{2}}}+{\frac {i\Delta t}{2}}V_{j}\right)\Psi _{j}^{n+1}-{\frac {i\Delta t}{4\Delta x^{2}}}\Psi _{j+1}^{n+1}-{\frac {i\Delta t}{4\Delta x^{2}}}\Psi _{j-1}^{n+1}=\left(1-{\frac {i\Delta t}{2\Delta x^{2}}}-{\frac {i\Delta t}{2}}V_{j}\right)\Psi _{j}^{n}+{\frac {i\Delta t}{4\Delta x^{2}}}\Psi _{j+1}^{n}+{\frac {i\Delta t}{4\Delta x^{2}}}\Psi _{j-1}^{n}$

Para simplificar, chamaremos ${\frac {i\Delta t}{4\Delta x^{2}}}$ de b. Nesse caso, temos:

 $\left(1+2b+{\frac {i\Delta t}{2}}V_{j}\right)\Psi _{j}^{n+1}-b\Psi _{j+1}^{n+1}-b\Psi _{j-1}^{n+1}=\left(1-2b-{\frac {i\Delta t}{2}}V_{j}\right)\Psi _{j}^{n}+b\Psi _{j+1}^{n}+b\Psi _{j-1}^{n}$

Definimos os Modos de Fourier:

$\Psi _{j}^{n}\approx A^{n}e^{iqjh}$

Assim, obtemos:

$\left(1+2b+{\frac {i\Delta t}{2}}V_{j}\right)A^{n+1}e^{iqjh}-bA^{n+1}e^{iq(j-1)h}-bA^{n+1}e^{iq(j+1)h}=\left(1-2b-{\frac {i\Delta t}{2}}V_{j}\right)A^{n}e^{iqjh}+bA^{n}e^{iq(j-1)h}+bA^{n}e^{iq(j+1)h}$

Dividindo tudo por $e^{iqjh}$ :

$\left(1+2b+{\frac {i\Delta t}{2}}V_{j}\right)A^{n+1}-bA^{n+1}e^{-iqh}-bA^{n+1}e^{iqh}=\left(1-2b-{\frac {i\Delta t}{2}}V_{j}\right)A^{n}+bA^{n}e^{-iqh}+bA^{n}e^{iqh}$

Escrito de outra forma:

$A^{n+1}\left[1+{\frac {i\Delta t}{2}}V_{j}-b(e^{-iqh}-2+e^{iqh})\right]=A^{n}\left[1+{\frac {i\Delta t}{2}}V_{j}+b(e^{-iqh}-2+e^{iqh})\right]$

Utilizando relações trigonométricas:

$A^{n+1}\left[1+{\frac {i\Delta t}{2}}V_{j}-b(-sin^{2}({\frac {qh}{2}}))\right]=A^{n}\left[1+{\frac {i\Delta t}{2}}V_{j}+b(-sin^{2}({\frac {qh}{2}}))\right]$

Assim, obtemos o fator de amplificação:

${\frac {A^{n+1}}{A^{n}}}={\frac {1+{\frac {i\Delta t}{2}}V_{j}-b(sin^{2}({\frac {qh}{2}}))}{1+{\frac {i\Delta t}{2}}V_{j}+b(sin^{2}({\frac {qh}{2}}))}}\leq 1$

Portanto, o método é estavel

Exemplos de Potenciais

Oscilador Harmônico

O oscilador harmônico quântico consiste de uma partícula em uma zona onde o potencial possui comportamento harmônico, ou seja, depende de $x^{2}$ . Em nosso exemplo, inserimos um pacote de formato gaussiano no interior de um potencial harmônico e observamos sua evolução temporal.

Abaixo encontra-se o código usado em Júlia.

using Plots

dt = 0.1
dx = 0.25
L = 50
x = collect(0:dx:L)
size(x)	

function V_Oh(x)
    return 0.005(x-L/2)^2
end

b = dt*im/(4*dx^2)
A = [if i==j; 1 - 2b  - V_Oh(i)*dt*im/2 elseif i==dx+j || i==j-dx; b else 0 end for i=0:dx:L, j=0:dx:L]
B = @. conj(A)
IB = inv(B)

len = length(x)
ψ = [(sqrt(1/(2*pi))*exp(-(val - L/3)^2/(2))*exp(-im*75*(val-L/3))) for val in x]  
for (i,num) in enumerate(ψ)
    if abs(num)<1e-10; 
        ψ[i]=0 
    end
end

ves = @. V_Oh(x)

t=0
@gif for t in 0:dt:65
    ψ[2:end-1] = IB[2:end-1,2:end-1]*A[2:end-1,2:end-1]*ψ[2:end-1]

    plot(x,abs2.(ψ),c="red")
    #plot!([x for x=0:dx:L],imag(ψ),c="blue")
    plot!([x for x=0:dx:L],ves,c="blue")
    plot!(ylim=[0,0.5],title="t=$t")
end every 3

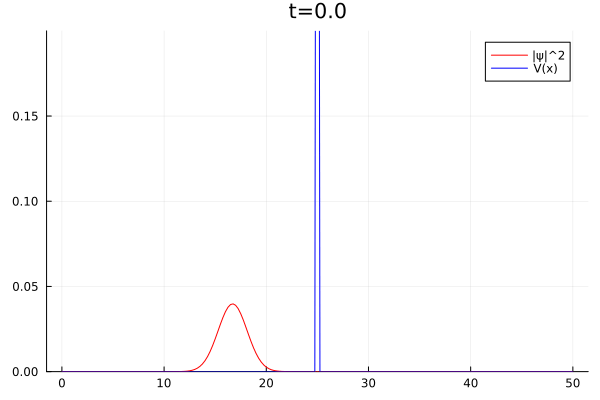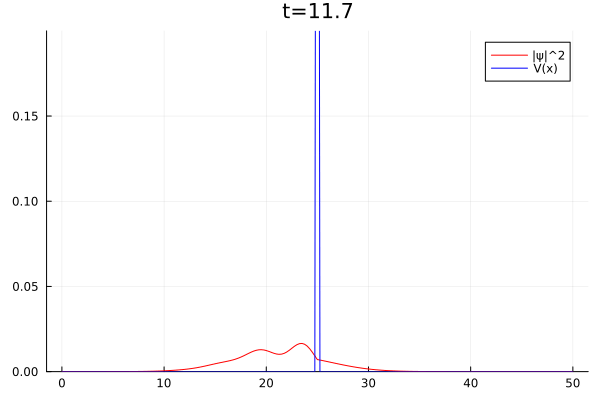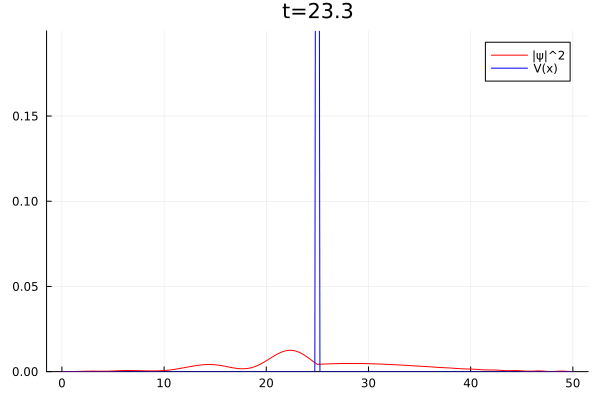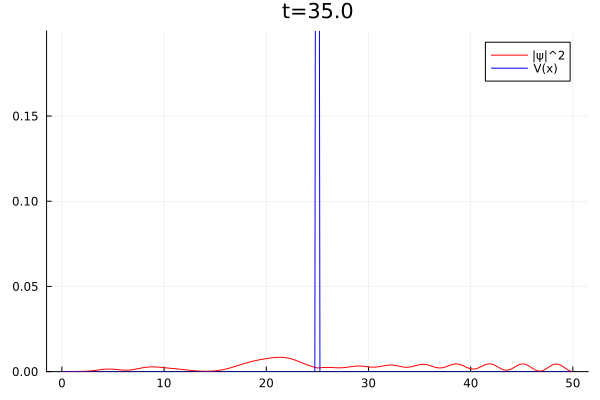
Barreira (Tunelamento)

Na mecânica quântica partículas podem existir, mesmo que com baixa probabilidade, em regiões que classicamente seriam proibidas. Este é o caso da barreira, onde uma partícula atravessa uma região onde sua energia total é negativa. Chamamos este fenômeno de tunelamento. A seguir, há um exemplo onde inserimos um pacote de formato gaussiano se deslocando em direção a uma barreira de potencial, de forma que parte da onda é refletida de volta e outra tunela pela barreira.

Abaixo encontra-se o código usado em Júlia.

using Plots

dt = 0.1
dx = 0.25
L = 50
x = collect(0:dx:L)
size(x)	

function V_b(x)
    if x==L/2
        return 1
    else
        return 0
    end
end

b = dt*im/(4*dx^2)
A_b = [if i==j; 1 - 2b  - V_b(i)*dt*im/2 elseif i==dx+j || i==j-dx; b else 0 end for i=0:dx:L, j=0:dx:L]
B_b = @. conj(A_b)
IB_b = inv(B_b)

len = length(x)
ψ = [(sqrt(1/(8*pi))*exp(-(val - L/3)^2/(8))*exp(-im*75*(val-L/3))) for val in x]  
for (i,num) in enumerate(ψ)
    if abs(num)<1e-10; 
        ψ[i]=0 
    end
end

ves_b = @. V_b(x)

t=0
@gif for t in 0:dt:35
    ψ[2:end-1] = IB_b[2:end-1,2:end-1]*A_b[2:end-1,2:end-1]*ψ[2:end-1]
for (i,num) in enumerate(ψ)
    if abs(num)<1e-10; 
        ψ[i]=0 
    end
end
    plot(x,abs2.(ψ),c="red",label="|ψ|^2")
    #plot!([x for x=0:dx:L],imag(ψ),c="blue")
    plot!([x for x=0:dx:L],ves_b,c="blue",label="V(x)")
    plot!(ylim=[0,0.2],title="t=$t")
end

Poço Finito

O contrário da barreira é o chamado de poço de potencial. Ao invés da partícula atravessá-lo por completo, uma parte do pacote de onda é refletido, uma parte é transmitido e outra ainda fica preso no meio do poço. Veja o exemplo.

Abaixo encontra-se o código usado em Júlia.

using Plots

dt = 0.1
dx = 0.25
L = 50
x = collect(0:dx:L)
size(x)	

function V_p(x)
    if x<L/3
        return 0.1
    elseif x>2L/3
        return 0.1
    else
        return 0
    end
end

b = dt*im/(4*dx^2)
A_p = [if i==j; 1 - 2b  - V_p(i)*dt*im/2 elseif i==dx+j || i==j-dx; b else 0 end for i=0:dx:L, j=0:dx:L]
B_p = @. conj(A_p)
IB_p = inv(B_p)

len = length(x)
ψ = [(sqrt(1/(8*pi))*exp(-(val - L/4)^2/(8))*exp(-im*75*(val-L/4))) for val in x]  
for (i,num) in enumerate(ψ)
    if abs(num)<1e-10; 
        ψ[i]=0 
    end
end

ves_p = @. V_p(x)

t=0
@gif for t in 0:dt:50
    ψ[2:end-1] = IB_p[2:end-1,2:end-1]*A_p[2:end-1,2:end-1]*ψ[2:end-1]
for (i,num) in enumerate(ψ)
    if abs(num)<1e-10; 
        ψ[i]=0 
    end
end
    plot(x,abs2.(ψ),c="red",label="|ψ|^2")
    #plot!([x for x=0:dx:L],imag(ψ),c="blue")
    plot!([x for x=0:dx:L],ves_p,c="blue",label="V(x)")
    plot!(ylim=[0,0.15],title="t=$t")
end

@@ Linha 64: / Linha 64: @@
 ==Estabilidade do Método de Crank-Nicolson==
+Para verificar a estabilidade, devemos primeiro olhar para a equação que define o método:
+ <math> \left(1+\frac{i \Delta t}{2 \Delta x^2}+\frac{i\Delta t}{2} V_j\right)\Psi_j^{n+1} - \frac{i \Delta t}{4 \Delta x^2}\Psi_{j+1}^{n+1} - \frac{i \Delta t}{4 \Delta x^2} \Psi_{j-1}^{n+1} = \left(1-\frac{i \Delta t}{2 \Delta x^2}-\frac{i\Delta t}{2} V_j\right)\Psi_{j}^{n} + \frac{i \Delta t}{4 \Delta x^2}\Psi_{j+1}^{n} +\frac{i \Delta t}{4 \Delta x^2} \Psi_{j-1}^{n}</math>
+Para simplificar, chamaremos <math>\frac{i \Delta t}{4 \Delta x^2}</math> de b. Nesse caso, temos:
+ <math> \left(1+2b+\frac{i\Delta t}{2} V_j\right)\Psi_j^{n+1} - b\Psi_{j+1}^{n+1} - b\Psi_{j-1}^{n+1} = \left(1-2b-\frac{i\Delta t}{2} V_j\right)\Psi_{j}^{n} + b\Psi_{j+1}^{n} +b\Psi_{j-1}^{n}</math>
+Definimos os Modos de Fourier:
+<math>\Psi_{j}^{n} \approx A^{n}e^{iqjh}</math>
+Assim, obtemos:
+<math> \left(1+2b+\frac{i\Delta t}{2} V_j\right)A^{n+1}e^{iqjh}- bA^{n+1}e^{iq(j-1)h} - bA^{n+1}e^{iq(j+1)h} = \left(1-2b-\frac{i\Delta t}{2} V_j\right)A^{n}e^{iqjh} + bA^{n}e^{iq(j-1)h} +bA^{n}e^{iq(j+1)h}</math>
+Dividindo tudo por <math>e^{iqjh}</math>:
+<math> \left(1+2b+\frac{i\Delta t}{2} V_j\right)A^{n+1}- bA^{n+1}e^{-iqh} - bA^{n+1}e^{iqh} = \left(1-2b-\frac{i\Delta t}{2} V_j\right)A^{n} + bA^{n}e^{-iqh} +bA^{n}e^{iqh}</math>
+Escrito de outra forma:
+<math> A^{n+1}\left[1+\frac{i\Delta t}{2} V_j -b(e^{-iqh}-2+e^{iqh})\right] = A^{n}\left[1+\frac{i\Delta t}{2} V_j +b(e^{-iqh}-2+e^{iqh})\right] </math>
+Utilizando relações trigonométricas:
+<math> A^{n+1}\left[1+\frac{i\Delta t}{2} V_j -b(-sin^2(\frac{qh}2))\right] = A^{n}\left[1+\frac{i\Delta t}{2} V_j +b(-sin^2(\frac{qh}2))\right]</math>
+Assim, obtemos o fator de amplificação:
+<math>\frac{A^{n+1}}{A^n} = \frac{1+\frac{i\Delta t}{2} V_j -b(sin^2(\frac{qh}2))}{1+\frac{i\Delta t}{2} V_j +b(sin^2(\frac{qh}2))} \leq 1</math>
+Portanto, o método é estavel
 == Exemplos de Potenciais ==

Equação de Schrödinger Unidimensional: mudanças entre as edições

Edição das 14h28min de 23 de abril de 2024

Índice

O Método De Crank-Nicolson

Estabilidade do Método de Crank-Nicolson

Exemplos de Potenciais

Oscilador Harmônico

Barreira (Tunelamento)

Poço Finito

Menu de navegação

Equação de Schrödinger Unidimensional: mudanças entre as edições

Edição das 14h28min de 23 de abril de 2024

O Método De Crank-Nicolson

Estabilidade do Método de Crank-Nicolson

Exemplos de Potenciais

Oscilador Harmônico

Barreira (Tunelamento)

Poço Finito

Menu de navegação

Pesquisa