Equação de Cahn-Hilliard em 2D: mudanças entre as edições
| Linha 63: | Linha 63: | ||
== Resultados em uma dimensão e discussão== | == Resultados em uma dimensão e discussão== | ||
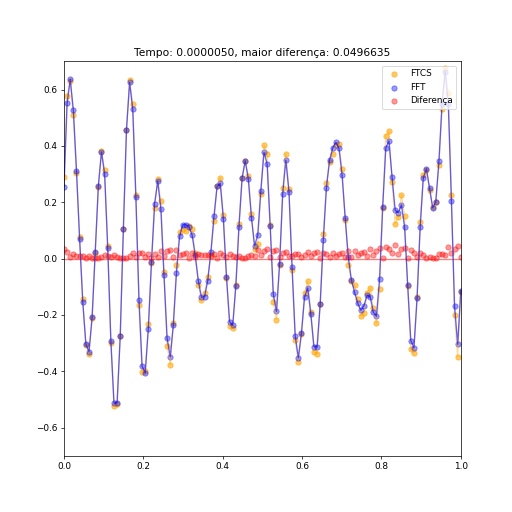
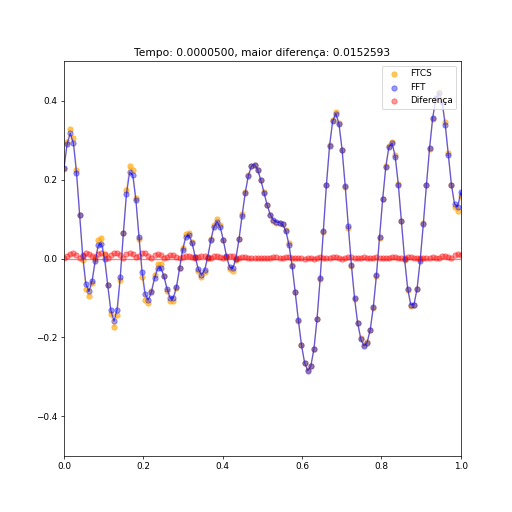
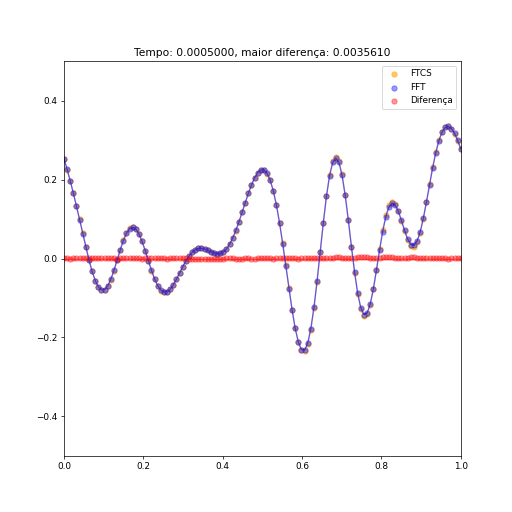
Como já há um trabalho que trata em detalhes a implementação unidimensional e seus resultados, irei comparar aqui ambas implementações. Abaixo, vemos alguns instantes comparando ambos métodos a partir de uma condição inicial aleatória, utillizando condições de contorno periódicas, com o maior valor de erro destacado no topo. O valor das constantes relevantes são: <math>\Delta t = \frac{1}{22 \ | Como já há um trabalho que trata em detalhes a implementação unidimensional e seus resultados, irei comparar aqui ambas implementações. Abaixo, vemos alguns instantes comparando ambos métodos a partir de uma condição inicial aleatória, utillizando condições de contorno periódicas, com o maior valor de erro destacado no topo. O valor das constantes relevantes são: <math>\Delta t = \frac{1}{22 \cdot 10^{6}}, \Delta x = \frac{1}{128}, D = 1, \gamma = (\frac{3.4}{128})^2, x_{max} = 1</math>. | ||
[[Arquivo:1d100passos.png]] [[Arquivo:1d1000passos.png]] [[Arquivo:1d10000.png]] | [[Arquivo:1d100passos.png]] [[Arquivo:1d1000passos.png]] [[Arquivo:1d10000.png]] | ||
Edição das 15h09min de 25 de setembro de 2022
Leonardo Dasso Migottto WORK IN PROGRESS
O objetivo deste trabalho é resolver computacionalmente a equação de Cahn-Hilliard, utilizando a Transformada Rápida de Fourier [1] em uma e (principalmente) em duas dimensões. Será explorado as variações em concentração inicial e seus respectivos padrões formados, dados coeficientes de difusão e largura da superfície fixos.
Esta equação já foi tratada em detalhes por colegas anteriores a mim [2], e a leitura do trabalho por eles desenvolvido é recomendada para maior entendimento da equação. O foco deste trabalho é explorar a solução numérica para a equação quando tratada em duas dimensões, onde a formação de padrões apresenta resultados mais interessantes. No entanto, a fim de facilitar a implementação e entendimento em duas dimensões, também será exibido uma implementação em uma dimensão.
Equação de Cahn-Hiliiard utilizando Transformada de Fourier
Para encontrar a equação que implementaremos com o uso da Transformada Rápida de Fourier, precisamos encontrar a nossa equação representada no espaço de Fourier. Seguirei a literatura de S. Bulent Biner [3], onde há um capítulo dedicado a resolver equações de difusão com métodos que utilizam esta transformada. Primeiro, resolveremos em uma dimensão a equação, que segue abaixo:
Em uma dimensão, os laplacianos podem ser substituídos pela derivada segunda em relação a , resultando na seguinte equação:
Para solucioná-la numericamente, aplicaremos a Transformada de Fourier à frente em ambos os lados, da maneira descrita abaixo, onde k é o respectivo coeficiente de Fourier):
Em seguida, substituimos as derivadas espaciais pela sua equivalente no espaço de Fourier:
Assim, obtemos a seguinte equação:
O próximo passo é fazer a derivada à direita quanto ao tempo da seguinte maneira:
Substituindo na equação e reescrevendo-a a fim de isolar , obtemos a equação final:
Dado que conhecemos a forma da equação em uma dimensão, podemos encontrar sua equivalente bidimensional com maior facilidade. A única diferença entre as duas equações está no laplaciano, que resultará na derivada no eixo aparecer também. No entanto, a notação da transformada permanece a mesma, e representará um vetor com coordenada com módulo , onde e são os coeficientes em e respectivamente.
Código em uma dimensão
O código completo está disponível no final desta página. Abaixo há o excerto da funcão, em Python, que calcula o instante seguinte do nosso sistema, utilizando as funções RFFT e IRFFT do pacote Scipy.
def cahnfourier1d(cc, k2, k4):
cct = rfft(cc)
cct3 = rfft(cc**3 - cc)
cct = cct + difd*dt*(-k2*(cct3) - k4*cct)
cc = irfft(cct)
return cc
No código, k2 e k4 são os coeficientes elevados às respectivas potências, porém k4 está multiplicado pelo valor de gamma. Calculando estas constantes préviamente é possível evitar cálculos reduntantes durante o código. É importante destacar que ambas funções funcionam utilizando o vetor completo de pontos para fazer os cálculos, eliminando qualquer necessidade de iteração sobre o vetor de valores (uma diferença notável do método FTCS).
Resultados em uma dimensão e discussão
Como já há um trabalho que trata em detalhes a implementação unidimensional e seus resultados, irei comparar aqui ambas implementações. Abaixo, vemos alguns instantes comparando ambos métodos a partir de uma condição inicial aleatória, utillizando condições de contorno periódicas, com o maior valor de erro destacado no topo. O valor das constantes relevantes são: .
Como podemos ver, a diferença dos valores entre os resultados obtidos pelo método FTCS e o método das transformadas é minúscula (após poucos instantes o maior módulo da diferença é menor que 0,01). É interessante citar que a escolha de como um valor tão específico não é em vão: a função RFFT utilizada no código apresenta maior rapidez de execução quando o vetor utilizado é de tamanho . Com este valor de , nosso vetor é composto de 128 elementos, ou elementos, fazendo uso dessa vantagem. Dado a escala do sistema na qual ambos métodos foram utilizados, os tempos de processamento são mínimos, e não há merito em compará-los. No entanto, para sistemas maiores, onde o número de operações necessárias aumenta drasticamente, o método das transformadas, sob as condições corretas, será extremamente rápido. E isso será observado com clareza quando o sistema for bidimensional.
Código em duas dimensões
Todos códigos estão disponíveis na íntegra no final desta página. A fim de poupar tempo, quatro programas foram criados:
- - Um programa que gera, a partir de valores aleatórios parametrizados, valores até um certo instante de tempo, salvando-os em um arquivo.
- - Um programa que, lê um arquivo de valores já gerados e gera mais valores até um certo instante de tempo, salvando-os neste mesmo arquivo.
- - Um programa que lê um arquivo gerado préviamente, criando uma animação dos valores salvos no arquivo.
- - Um programa que lê um arquivo gerado préviamente, criando frames dos valores salvos no arquivo.
Um padrão de arquivo de formato .npy é foi criado, que armazena as informações necessárias para gerar mais valores ou plotar os gráficos, atém de um .txt que serve como uma consulta local dos valores pelo usuário (arquivos .npy não podem ser lidos sem um código). Um arquivo .npy com tais informações é salvo para ser lido pelos programas. Todos arquivos são salvos em pastas individuias cujo nome é um número aleatório único, sendo este número o nome do arquivo de texto e o arquivo com os valores calculados. Abaixo há o excerto da funcão, em Python, que calcula o instante seguinte do nosso sistema, utilizando as funções RFFT2 e IRFFT2 do pacote Scipy.
def cahnfourier2d(aa, kk2, kk4):
cct = rfft2(aa)
cct3 = rfft2(aa**3)
cct = cct + difd*dt*(-kk2*(cct3 - cct) - kk4*cct)
ccn = irfft2(cct)
return ccn
No código, kk2 e kk4 são os coeficientes elevados às respectivas potências, porém kk4 está multiplicado pelo valor de gamma. Vale destacar a semelhança entre este código e o unidimensional, fruto da discretização quase idêntica.
Resultados em duas dimensões
Para todos resultados abaixo, foram utilizados as seguintes constantes relevantes: . Também foram utilizadas condições de contorno periódicas. Como observado anteriormente, o valor de escolhido serve para que nosso array de valores possua elementos, também fazendo uso da eficiência completa da função RFFT2 (equivalente bidimensional da função RFFT). Segue abaixo uma IMAGEM ? da difusão sob estes parâmetros com concentração média 0.
INSERIR IMAGEM AQUI (NÃO PODE GIF, MUITO PESADO)
Aqui há uma animação de um gráfico com concentração média inicial 0.5 (como se houvesse 75% em uma fase e 25% em outra).
Discussão dos resultados em duas dimensões
Podemos notar que há a formação de "listras" conforme passa o tempo, de modo que estas listras tornam-se mais largas. Também nota-se que, quanto mais tempo se passa, menor é o movimento das concentrações, por elas estarem se aproximando da estabilidade. É intuitivo que, neste caso, o estado de equilíbrio do sistema seja quando há somente dois "blocos", um de cada cor, de modo que as "listras" (dois grandes blocos, neste caso) não tenham como se tornar mais largas.
Referências
- ↑ https://fiscomp.if.ufrgs.br/index.php/FFT
- ↑ https://fiscomp.if.ufrgs.br/index.php/Equa%C3%A7%C3%A3o_de_Cahn-Hilliard
- ↑ S_Bulent_Biner_Programming_Phase_Field_Modeling_Springer_2017