Belousov-Zhabotinsky: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 1: | Linha 1: | ||
== Belousov-Zhabotinsky Reaction == | == Belousov-Zhabotinsky Reaction == | ||
A reação de Belousov-Zhabotinsky (BZ) consiste em uma família de reações químicas oscilatórias descobertas inicialmente por Belousov, e posteriormente analisadas por Zhabotinsky. A reação consiste em 3BrO<sub>3</sub><sup>−</sup> + 5CH<sub>2</sub>(CO<sub>2</sub>H)<sub>2</sub> + 3H<sup>+</sup> → 3BrCH(CO<sub>2</sub>H)<sub>2</sub> + 4CO<sub>2</sub> + 5H<sub>2</sub>O + 2CH<sub>2</sub>O<sub>2</sub>, e demonstra um comportamento oscilatório não linear até atingir o equilíbrio químico. A interação entre a reação e a difusão dos produtos químicos no espaço resultará na auto-organização de ondas viajantes dinâmicas. Seu mecanismo original, foi descrito através de 27 espécies químicas e um total de 80 reações. | A reação de Belousov-Zhabotinsky<ref name=Sayama260>H. Sayama, "Introduction to the Modeling and Analysis of Complex Systems", p. 287. Open SUNY Textbooks, Geneseo, NY, 2015.</ref> <ref name=Paper>HArzola-Flores J.A., García E., Rojas J.F, Spatial and temporal dynamics of Belousov-Zhabotinsky reaction: A STEM approach (2020), Revista Mexicana de Física E 17 (2) 178–190 </ref> (BZ) consiste em uma família de reações químicas oscilatórias descobertas inicialmente por Belousov, e posteriormente analisadas por Zhabotinsky. A reação consiste em 3BrO<sub>3</sub><sup>−</sup> + 5CH<sub>2</sub>(CO<sub>2</sub>H)<sub>2</sub> + 3H<sup>+</sup> → 3BrCH(CO<sub>2</sub>H)<sub>2</sub> + 4CO<sub>2</sub> + 5H<sub>2</sub>O + 2CH<sub>2</sub>O<sub>2</sub>, e demonstra um comportamento oscilatório não linear até atingir o equilíbrio químico. A interação entre a reação e a difusão dos produtos químicos no espaço resultará na auto-organização de ondas viajantes dinâmicas. Seu mecanismo original, foi descrito através de 27 espécies químicas e um total de 80 reações. | ||
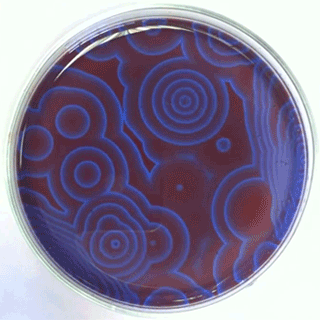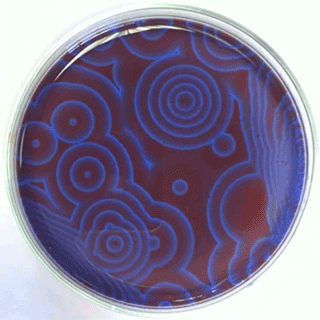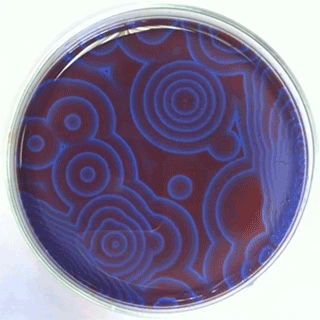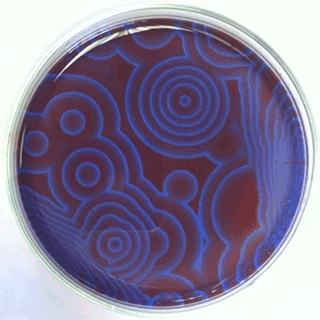
[[Arquivo:BZReaction.gif|thumb|center|none|alt=Alt text|Reação de Belousov-Zhabotinsky em uma placa de Petri.|480px]] | [[Arquivo:BZReaction.gif|thumb|center|none|alt=Alt text|Reação de Belousov-Zhabotinsky em uma placa de Petri.|480px]] | ||
== Oregonator == | == Oregonator == | ||
Oregonator é um modelo matemático utilizado para descrever de forma mais simples a dinâmica da reação BZ, desenvolvido por Field e Noyes (1974). Foi um modelo não espacial originalmente composto por três variáveis de estado, onde posteriormente, vemos que tornam-se apenas duas. O mecanismo é, inicialmente composto por cinco etapas irreversíveis, onde, A = 3BrO<sub>3</sub> <sup>-</sup>, B = 5CH<sub>2</sub>(COOH)<sub>2</sub>; 2HCOOH, 3BrCH(COOH)<sub>2</sub> (no geral, estas e demais espécies orgânicas); P = HOBr; X = HBrO<sub>2</sub>; Y = Br<sup>-</sup>; Z = forma oxidada do catalisador e f = Coeficiente estequiométrico. | Oregonator<ref name=Paper>HArzola-Flores J.A., García E., Rojas J.F, Spatial and temporal dynamics of Belousov-Zhabotinsky reaction: A STEM approach (2020), Revista Mexicana de Física E 17 (2) 178–190 </ref> é um modelo matemático utilizado para descrever de forma mais simples a dinâmica da reação BZ, desenvolvido por Field e Noyes (1974). Foi um modelo não espacial originalmente composto por três variáveis de estado, onde posteriormente, vemos que tornam-se apenas duas. O mecanismo é, inicialmente composto por cinco etapas irreversíveis, onde, A = 3BrO<sub>3</sub> <sup>-</sup>, B = 5CH<sub>2</sub>(COOH)<sub>2</sub>; 2HCOOH, 3BrCH(COOH)<sub>2</sub> (no geral, estas e demais espécies orgânicas); P = HOBr; X = HBrO<sub>2</sub>; Y = Br<sup>-</sup>; Z = forma oxidada do catalisador e f = Coeficiente estequiométrico. | ||
{| | {| | ||
| Linha 50: | Linha 50: | ||
|} | |} | ||
Onde <math>\epsilon \equiv \tfrac{k_{5}[B]}{k-{3}[A]}</math>, <math> \epsilon ' \equiv \tfrac{2k_{4}k_{5}[B]}{k_{2}k_{3}[A]}</math> e <math>q \equiv \tfrac{2k_{4}k_{1}}{k_{2}k_{3}}</math>. Como parâmetro <math>\epsilon' \approx 10^{-5}</math>, é possível considerar a aproximação do estado estacionário da variável y, portanto, <math>y \equiv \tfrac{fz}{q+x}</math> então as equações são reduzidos para: | Onde <math>\epsilon \equiv \tfrac{k_{5}[B]}{k-{3}[A]}</math>, <math> \epsilon ' \equiv \tfrac{2k_{4}k_{5}[B]}{k_{2}k_{3}[A]}</math> e <math>q \equiv \tfrac{2k_{4}k_{1}}{k_{2}k_{3}}</math>. Como parâmetro <math>\epsilon' \approx 10^{-5}</math>, é possível considerar a aproximação do estado estacionário da variável y<ref name=Oreg>http://www.scholarpedia.org/article/Oregonator#Eq-4</ref> | ||
, portanto, <math>y \equiv \tfrac{fz}{q+x}</math> então as equações são reduzidos para: | |||
: <math> \epsilon \frac{dx}{dt}= x(1-x) + f\frac{q-x}{q+x}z </math> | : <math> \epsilon \frac{dx}{dt}= x(1-x) + f\frac{q-x}{q+x}z </math> | ||
| Linha 67: | Linha 68: | ||
Antes de discretizarmos a equação para que assim possamos utiliza-la em um código, explicaremos brevemente métodos e fórmulas utilizados para isso. | Antes de discretizarmos a equação para que assim possamos utiliza-la em um código, explicaremos brevemente métodos e fórmulas utilizados para isso. | ||
=== Método FTCS (Forward Time Centered Space) === | === Método FTCS (Forward Time Centered Space)<ref name=wiki>https://pt.wikipedia.org/wiki/Esquema_FTCS</ref> === | ||
De modo a resolver numericamente as equações descritas acima, serão utilizado o método FTCS (Forward Time Centered Space), que consiste em um método para resolver equações parciais através da derivada parcial de primeira ordem no tempo por uma diferença finita e progressiva e a derivada parcial de segunda ordem no espaço por uma diferença centrada, como vemos logo abaixo: | De modo a resolver numericamente as equações descritas acima, serão utilizado o método FTCS (Forward Time Centered Space), que consiste em um método para resolver equações parciais através da derivada parcial de primeira ordem no tempo por uma diferença finita e progressiva e a derivada parcial de segunda ordem no espaço por uma diferença centrada, como vemos logo abaixo: | ||
| Linha 92: | Linha 93: | ||
:<math> u_{i,j}^{n+1} = u_{C} + \left[u_{C}(1-u_{C}) + f\frac{q-u_{C}}{q+u_{C}}v_{C} + D_{u} \left(\frac{u_{R}+u_{L}+u_{U}+u_{D}-4u_{C}}{Dh^{2}}\right)\right]\frac{Dt}{\epsilon}</math> | :<math> u_{i,j}^{n+1} = u_{C} + \left[u_{C}(1-u_{C}) + f\frac{q-u_{C}}{q+u_{C}}v_{C} + D_{u} \left(\frac{u_{R}+u_{L}+u_{U}+u_{D}-4u_{C}}{Dh^{2}}\right)\right]\frac{Dt}{\epsilon}</math> | ||
| Linha 111: | Linha 111: | ||
== teste == | == teste == | ||
condições iniciais | condições iniciais | ||
| Linha 124: | Linha 124: | ||
<math> v_{i,j}^{n+1} = v_{i,j}^{n} + (u_{i,j}^{n} - v_{i,j}^{n} + \nabla v (\frac{(v_{i+1,j}^{n} + v_{i-1,j}^{n} + v_{i,j+1}^{n} + v_{i,j-1}^{n} - 4v_{i,j}^{n})}{Dh^2})dt </math> | <math> v_{i,j}^{n+1} = v_{i,j}^{n} + (u_{i,j}^{n} - v_{i,j}^{n} + \nabla v (\frac{(v_{i+1,j}^{n} + v_{i-1,j}^{n} + v_{i,j+1}^{n} + v_{i,j-1}^{n} - 4v_{i,j}^{n})}{Dh^2})dt </math> | ||
== Referências == | |||
<references/> | |||
Edição das 10h30min de 30 de março de 2021
Belousov-Zhabotinsky Reaction
A reação de Belousov-Zhabotinsky[1] [2] (BZ) consiste em uma família de reações químicas oscilatórias descobertas inicialmente por Belousov, e posteriormente analisadas por Zhabotinsky. A reação consiste em 3BrO3− + 5CH2(CO2H)2 + 3H+ → 3BrCH(CO2H)2 + 4CO2 + 5H2O + 2CH2O2, e demonstra um comportamento oscilatório não linear até atingir o equilíbrio químico. A interação entre a reação e a difusão dos produtos químicos no espaço resultará na auto-organização de ondas viajantes dinâmicas. Seu mecanismo original, foi descrito através de 27 espécies químicas e um total de 80 reações.
Oregonator
Oregonator[2] é um modelo matemático utilizado para descrever de forma mais simples a dinâmica da reação BZ, desenvolvido por Field e Noyes (1974). Foi um modelo não espacial originalmente composto por três variáveis de estado, onde posteriormente, vemos que tornam-se apenas duas. O mecanismo é, inicialmente composto por cinco etapas irreversíveis, onde, A = 3BrO3 -, B = 5CH2(COOH)2; 2HCOOH, 3BrCH(COOH)2 (no geral, estas e demais espécies orgânicas); P = HOBr; X = HBrO2; Y = Br-; Z = forma oxidada do catalisador e f = Coeficiente estequiométrico.
| A + Y | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \longrightarrow} | X + P | ||
| X + Y | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \longrightarrow} | 2 P | ||
| A + X | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \longrightarrow} | 2 X + 2 Z | ||
| 2 X | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \longrightarrow} | A + P | ||
| B + Z | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \longrightarrow} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}f} Y |
Aplicando, então, as equações de taxa, onde v é a taxa da reação e ki corresponde às constantes de taxa de reação:
| v1 = k1 [A][Y] | v2 = k2 [X][Y] | v3 = k3 [A][X] | v4 = k4 [X]2 | v5 = k5 [B][Z] |
Para construir o modelo Oregonator, é necessário supor que as concentrações de A e B permaneçam constantes (estão associadas às concentrações iniciais dos precursores). Posteriormente, deve-se aplicar as técnicas padrão de cinética química para obter o modelo dinâmico considerando X, Y e Z como variáveis dinâmicas, assumindo que as reações químicas são elementares, ou seja, os coeficientes estequiométricos coincidem com a potência das variáveis dinâmicas. Considerando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} como o tempo, vemos as seguintes equações de velocidade:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d [X]}{d\tau}= k_1 [A] [Y] - k_{2} [X] [Y] + k_{3} [A] [X] - 2k_{4} [X]^2 }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d [Y]}{d\tau}= -k_1 [A] [Y] - k_{2} [X] [Y] + \frac{1}{2}f k_5 [B] [Z]}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d [Z]}{d\tau}= 2k_{3} [A] [X] - k_5 [B] [Z] }
A análise é simplificada convertendo essas equações em uma forma adimensional:
| Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \equiv \tfrac{2k_{4}[X]}{k_{3}[Y]}} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y \equiv \tfrac{k_{2}[X]}{k_{3}[A]}} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z \equiv \tfrac{k_{5}k_{4}[B][Z]}{(k_{3}[A])^{2}}} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t \equiv k_{5}[B] \tau} |
A partir de operações algébricas com as equações acima, obtemos para x, y e z, o seguinte sistema de equações diferenciais não lineares:
| Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{dx}{dt} = \tfrac{qy - xy + x(1-x)}{\epsilon}} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{dy}{dt} = \tfrac{-qy - xy + fz}{\epsilon '}} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{dz}{dt} = x - z} |
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \equiv \tfrac{k_{5}[B]}{k-{3}[A]}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon ' \equiv \tfrac{2k_{4}k_{5}[B]}{k_{2}k_{3}[A]}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q \equiv \tfrac{2k_{4}k_{1}}{k_{2}k_{3}}} . Como parâmetro Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon' \approx 10^{-5}} , é possível considerar a aproximação do estado estacionário da variável y[3] , portanto, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y \equiv \tfrac{fz}{q+x}} então as equações são reduzidos para:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \frac{dx}{dt}= x(1-x) + f\frac{q-x}{q+x}z }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dz}{dt}= x-z}
Dessa forma, o modelo de Oregonator mostra a forma típica de um sistema de feedback químico, ou seja, a variável x, que será reescrito como u, funciona como um ativador, enquanto a variável z, que será reescrita como v, tem o papel de inibidor. Se para as equações termos associados à difusão são adicionados, onde Du e Dv são os coeficientes de difusão adimensionais, e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^{2}}
é o operador Laplaciano, então, o sistema torna-se:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \frac{du}{dt}= u(1-u) + f\frac{q-u}{q+u}v + D_{u} \nabla^{2}u}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dv}{dt}= u-v + D_{v} \nabla^{2}v}
Implementação
Antes de discretizarmos a equação para que assim possamos utiliza-la em um código, explicaremos brevemente métodos e fórmulas utilizados para isso.
Método FTCS (Forward Time Centered Space)[4]
De modo a resolver numericamente as equações descritas acima, serão utilizado o método FTCS (Forward Time Centered Space), que consiste em um método para resolver equações parciais através da derivada parcial de primeira ordem no tempo por uma diferença finita e progressiva e a derivada parcial de segunda ordem no espaço por uma diferença centrada, como vemos logo abaixo:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f}{\partial t} \approx \frac{f(h,t+dt) - f(h,dt)}{\Delta t} = \frac{f_{i}^{n+1} - f_{i}^{n}}{\Delta t}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^{2}f}{\partial h^{2}} \approx \frac{f(h, t-dt) - 2f(h, t) + f(h, t+1)}{\Delta h^{2}} = \frac{f_{i}^{n-1} - 2f_{i}^{n} + f_{i}^{n+1}}{\Delta h^{2}}}
Laplaciano
...para a aplicação em vetores de duas dimensões, o laplaciano será aplicado desta forma:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^{2}f(h,t) = \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2}f}{\partial y^{2}}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^{2}f(h,t) = \frac{f(x+dh,y,t)+f(x-dh,y,t)+f(x,y+dh,t)+f(x,y-dh,t)-4f(x,y,t)}{dh^{2}} }
De modo a simplificar a expressão para analises posteriores, reescreveremos desta forma, considerando uma analise 2D:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^{2}f(h,t) = \frac{f_{R}+f_{L}+f_{U}+f_{D}-4f_{C}}{dh^{2}} }
Aplicação dos Métodos para a Reação de Belousov-Zhabotinsky
Considerando a equação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \frac{\partial u}{\partial t}= u(1-u) + f\frac{q-u}{q+u}v + D_{u} \nabla^{2}u} :
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \frac{u_{i,j}^{n+1} - u_{i,j}^{n}}{Dt}= u_{C}(1-u_{C}) + f\frac{q-u_{C}}{q+u_{C}}v_{C} + D_{u} \left(\frac{u_{R}+u_{L}+f_{U}+u_{D}-4u_{C}}{Dh^{2}}\right)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{i,j}^{n+1} - u_{i,j}^{n}= \left[u_{C}(1-u_{C}) + f\frac{q-u_{C}}{q+u_{C}}v_{C} + D_{u} \left(\frac{u_{R}+u_{L}+u_{U}+u_{D}-4u_{C}}{Dh^{2}}\right)\right]\frac{Dt}{\epsilon}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{i,j}^{n+1} = u_{C} + \left[u_{C}(1-u_{C}) + f\frac{q-u_{C}}{q+u_{C}}v_{C} + D_{u} \left(\frac{u_{R}+u_{L}+u_{U}+u_{D}-4u_{C}}{Dh^{2}}\right)\right]\frac{Dt}{\epsilon}}
Considerando a equação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial v}{\partial t}= u-v + D_{v} \nabla^{2}v}
:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{v_{i,j}^{n+1} - v_{i,j}^{n}}{Dt}= u_{C}-v_{C} + D_{v} \left(\frac{v_{R}+v_{L}+v_{U}+v_{D}-4v_{C}}{Dh^{2}}\right) }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{i,j}^{n+1} - v_{i,j}^{n}= \left[ u_{C}-v_{C} + D_{v} \left(\frac{v_{R}+v_{L}+v_{U}+v_{D}-4v_{C}}{Dh^{2}} \right)\right] Dt }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{i,j}^{n+1} = v_{C} + \left[ u_{C}-v_{C} + D_{v} \left(\frac{v_{R}+v_{L}+v_{U}+v_{D}-4v_{C}}{Dh^{2}} \right)\right] Dt }
teste
condições iniciais
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{i,j}^{0} = 1 } se 0 < 8(0.01i - 0.5) < (0.01j - 0.5) senão = 0
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{i,j}^{0} = 1 } se 0 < -(0.01j - 0.5) < 8(0.01i - 0.5) senão = 0
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{i,j}^{n+1} = u_{i,j}^{n} + \frac{(u_{i,j}^{n}( 1 - u_{i,j}^{n}) - fv_{i,j}^{n}(u_{i,j}^{n} - q)}{(u_{i,j}^{n} + q) + \nabla u(\frac{(u_{i+1,j}^{n} + u_{i-1,j}^{n} + u_{i,j+1}^{n} + u_{i,j-1}^{n} - 4u_{i,j}^{n})}{Dh^2})}\frac{dt}{e} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{i,j}^{n+1} = v_{i,j}^{n} + (u_{i,j}^{n} - v_{i,j}^{n} + \nabla v (\frac{(v_{i+1,j}^{n} + v_{i-1,j}^{n} + v_{i,j+1}^{n} + v_{i,j-1}^{n} - 4v_{i,j}^{n})}{Dh^2})dt }
Referências
- ↑ H. Sayama, "Introduction to the Modeling and Analysis of Complex Systems", p. 287. Open SUNY Textbooks, Geneseo, NY, 2015.
- ↑ 2,0 2,1 HArzola-Flores J.A., García E., Rojas J.F, Spatial and temporal dynamics of Belousov-Zhabotinsky reaction: A STEM approach (2020), Revista Mexicana de Física E 17 (2) 178–190
- ↑ http://www.scholarpedia.org/article/Oregonator#Eq-4
- ↑ https://pt.wikipedia.org/wiki/Esquema_FTCS