Pêndulos Estocásticos: mudanças entre as edições
| Linha 142: | Linha 142: | ||
[[Arquivo:Power.png|frame|center|Potência em função do ruído (<math>\alpha</math>). O painel da esquerda possui eixos em escala linear e o da direita em escala logarítmica.]] | [[Arquivo:Power.png|frame|center|Potência em função do ruído (<math>\alpha</math>). O painel da esquerda possui eixos em escala linear e o da direita em escala logarítmica.]] | ||
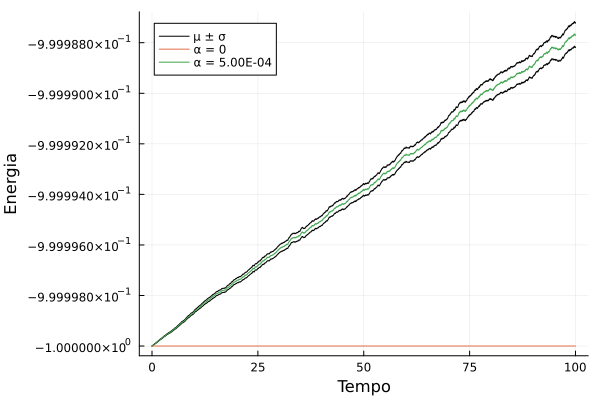
Portanto, <math>\bar P</math> aumenta, aproximadamente, de forma quadrática com <math>\alpha</math>. | Portanto, <math>\bar P</math> aumenta, aproximadamente, de forma quadrática com <math>\alpha</math>. Por fim, gostaríamos de mostrar que mesmo para <math> \alpha</math> muito pequeno, ainda existe energia sendo injetada no sistema com taxa constante, e isso não é um artefato da simulação. Para tal, foram realizadas 700 simulações com <math>\alpha=5\cdot10^{-4}</math> e os resultados foram comparados com <math> \alpha = 0</math> | ||
[[Arquivo:Test_low_alpha.png|frame|center|Energia média para <math>\alpha</math> muito pequeno comparado com <math>\alpha</math> nulo.]] | |||
===Energia (Com amortecimento)=== | ===Energia (Com amortecimento)=== | ||
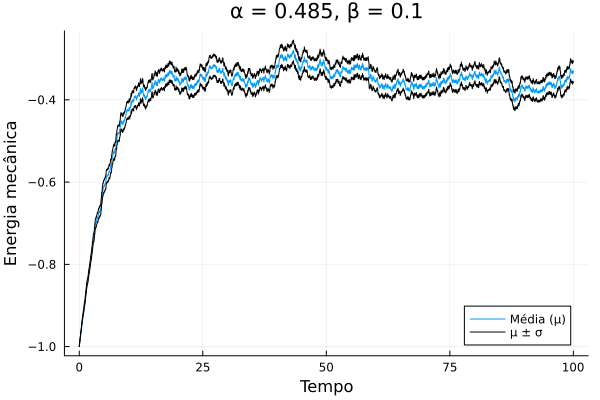
Até o momento, o amortecimento foi negligenciado. Vamos, então, introduzi-lo e rodar várias simulações (700, neste caso) e observar como a média temporal da energia evolui ao longo do tempo, assim como foi feita na seção anterior. Utilizando <math>\beta =0.1</math> e <math>\alpha = 0.485</math> foi obtido o seguinte resultado | |||
[[Arquivo:Energy_beta_example.png|frame|center|Energia mecânica média em função do tempo com amortecimento.]] | |||
claramente o comportamento neste caso é diferente do observado sem amortecimento, agora a anergia aumenta até um certo valor e permanece nele. Para explorar este novo fenômeno, os seguintes passos foram feitos para cada valor de <math>\beta = 0.01, 0.1, 0.2 </math>: | |||
* Para diversos valores de <math>\alpha</math>, executar 700 simulações até a energia estabilizar, salvando a média da energia entre as simulações. | |||
* Para cada conjunto de dados gerados por um determinado <math>\alpha</math>, selecionar um intervalo de tempo onde a energia está estabilizada e calcular a sua média (<math>\langle E \rangle</math>). | |||
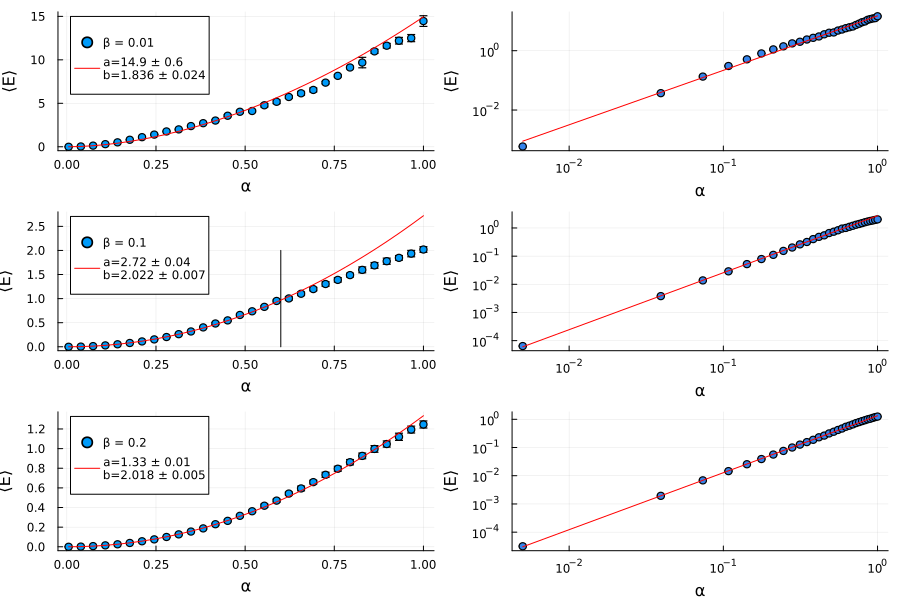
Produzindo o gráfico de <math>\langle E \rangle \times \alpha</math> obtemos | |||
[[Arquivo:Power_beta_mosaic.png|frame|center|Energia estabilizada média em função de <math>\alpha</math> para diferentes valores de amortecimento. Os painéis da esquerda possui eixos em escala linear e os da direita em escala logarítmica.]] | |||
as linhas vermelhas são os melhores ajustas de leis de potência na forma <math>\langle E \rangle = a \alpha^b </math>. Para <math>\beta=0.1</math> os dados utilizados no ajuste foram apenas até <math>\alpha = 0.6</math> (indicado pela reta preta vertical no gráfico), pois após esse limite, a lei de potência deixa de ser um ótimo ajuste. É chamativo o fato de todos os coeficientes, independente de <math>\beta</math>, serem aproximadamente 2. | |||
Edição das 23h47min de 19 de agosto de 2024
Grupo : Gustavo H. Guesser, Joshua L. Kipper, Marcos Pasa.
Pêndulo Simples
Equação de movimento
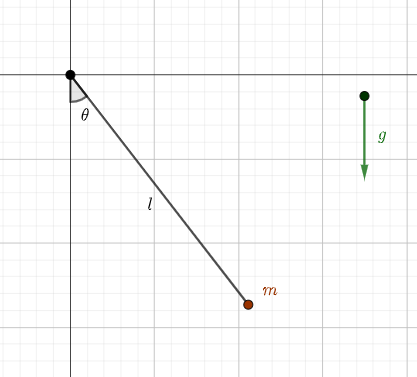
Primeiramente vamos inserir ruído em um pêndulo simples, que é constituído de uma barra de comprimento , sem massa e rígida que contém uma massa pontual em sua ponta, conforme ilustrado na figura a seguir.
Considerando que o pêndulo está sob o efeito da gravidade e se encontra submerso em um fluido viscoso (como o ar), tal que a força de resistência que atua na massa é , a equação de movimento é dada por:
Vamos supor que existe uma força ruidosa atuando em (), que pode ser modelada por um ruído branco gaussiano da seguinte forma
em que é a intensidade do ruído. é caracterizado pelas seguintes propriedades:
Adicionando essa nova força nas equações de movimento, ficamos com
A partir de agora, por questão de simplicidade, vamos supor que , então
Método de integração
Vamos montar um métodos para integrar o sistema no tempo. Primeiramente vamos dividir a equação em duas equações diferencias de primeira ordem, introduzindo a variável , então ficamos com o seguinte sistema
que pode ser escrito na forma diferencial
mas é o incremento do processo de Wiener (), então
Discretizando o tempo e lembrando que a densidade de probabilidade de transição de para tem desvio padrão igual a
em que é uma amostra de uma distribuição gaussiana com média 0 e variância 1, e o método de Euler foi utilizado para a parte determinística da equação.
Nas próximas seções será analisado a energia do sistema, e como o método de Euler não é muito bom para preservar a energia de sistemas conservativos, será utilizado o método preditor corretor (com adição do método de Heun para ) para a parte determinística da equação, que consiste nos seguintes passos:
- Calcular um theta intermediário:
- Com calcular um theta médio e utilizá-lo para obter um omega intermediário:
- Em que é a expressão do método de Euler visto logo acima.
- Recalcular theta utilizando um omega intermediário
- Recalcular omega com um theta intermediário atualizado
- OBS: No cálculo de e foi utilizado o mesmo .
Energia (Sem amortecimento)
Logo após terminar a implementação do método numérico, rapidamente notamos que a adição do ruído aumento a energia mecânica do pêndulo (), vamos explorar esse fenômeno, sempre utilizando . Para ilustrar esse efeito, segue uma animação do pêndulo partindo do repouso na configuração de equilíbrio estável () com
Para realizar uma exploração quantitativa, o seguinte procedimento foi feito para vários valores de :
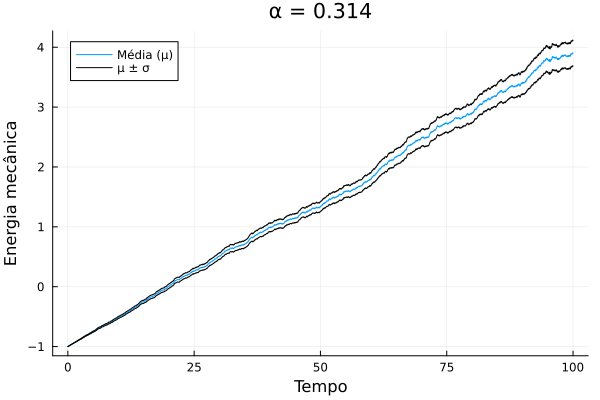
- Utilizando , integrar o sistema até , calculando e armazenando a energia em cada passo temporal. Repetir essa integração 700 vezes para fazer médias temporais. Como exemplo, segue os dados obtidos da energia em função do tempo (com a média temporal feita) para um determinado utilizado
- O gráfico nos indica que o ruído gera uma potência média sobre o pêndulo.
- Realizar um ajuste linear nos dados para obter o coeficiente angular, que corresponde a potência média gerada pelo ruído ().
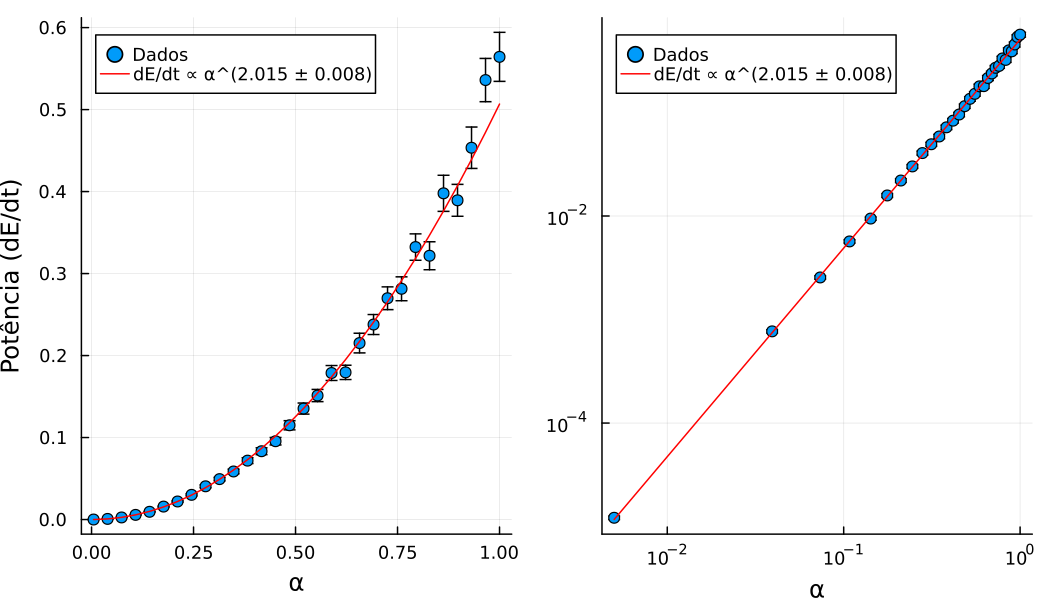
Com as simulações executadas, foi realizado o gráfico . Notamos que os dados se alinham em linha reta com os eixos em escala logarítmica, ou seja, os mesmos seguem uma lei de potência ), então foi realizado outro ajuste linear para encontra o expoente , a figura a seguir ilustra os dados e os resultados do ajuste:
Portanto, aumenta, aproximadamente, de forma quadrática com . Por fim, gostaríamos de mostrar que mesmo para muito pequeno, ainda existe energia sendo injetada no sistema com taxa constante, e isso não é um artefato da simulação. Para tal, foram realizadas 700 simulações com e os resultados foram comparados com
Energia (Com amortecimento)
Até o momento, o amortecimento foi negligenciado. Vamos, então, introduzi-lo e rodar várias simulações (700, neste caso) e observar como a média temporal da energia evolui ao longo do tempo, assim como foi feita na seção anterior. Utilizando e foi obtido o seguinte resultado
claramente o comportamento neste caso é diferente do observado sem amortecimento, agora a anergia aumenta até um certo valor e permanece nele. Para explorar este novo fenômeno, os seguintes passos foram feitos para cada valor de :
- Para diversos valores de , executar 700 simulações até a energia estabilizar, salvando a média da energia entre as simulações.
- Para cada conjunto de dados gerados por um determinado , selecionar um intervalo de tempo onde a energia está estabilizada e calcular a sua média ().
Produzindo o gráfico de obtemos
as linhas vermelhas são os melhores ajustas de leis de potência na forma . Para os dados utilizados no ajuste foram apenas até (indicado pela reta preta vertical no gráfico), pois após esse limite, a lei de potência deixa de ser um ótimo ajuste. É chamativo o fato de todos os coeficientes, independente de , serem aproximadamente 2.