Pêndulos Estocásticos

Grupo : Gustavo H. Guesser, Joshua L. Kipper, Marcos Pasa.

Pêndulo Simples

Equação de movimento

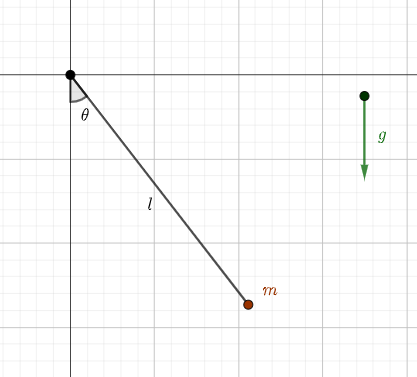
Primeiramente vamos inserir ruído em um pêndulo simples, que é constituído de uma barra de comprimento $l$, sem massa e rígida que contém uma massa $m$ pontual em sua ponta, conforme ilustrado na figura a seguir.

Esquema de um pêndulos simples em um campo gravitacional constante.

Considerando que o pêndulo está sob o efeito da gravidade e se encontra submerso em um fluido viscoso (como o ar), tal que a força de resistência que atua na massa é $-2b\overrightarrow{v}$, a equação de movimento é dada por:

$\ddot{\theta }(t)=-\frac{2b}{m}\dot{\theta }-\frac{g}{l}sen(\theta )$

Vamos supor que existe uma força ruidosa atuando em $m$ ($F_r(t)$), que pode ser modelada por um ruído branco gaussiano $\xi (t)$ da seguinte forma

$F_r(t)=m\alpha \xi (t)$

em que $\alpha$ é a intensidade do ruído. $\xi (t)$ é caracterizado pelas seguintes propriedades:

$⟨\xi (t)⟩=0,⟨\xi (t_2)\xi (t_1)⟩=\delta (t_2-t_1)$

Adicionando essa nova força nas equações de movimento, ficamos com

$\ddot{\theta }(t)=-\frac{2b}{m}\dot{\theta }-\frac{g}{l}sen(\theta )+\frac{\alpha }{l}\xi (t)$

A partir de agora, por questão de simplicidade, vamos supor que $g=l=1$, então

$\ddot{\theta }(t)=-2b\dot{\theta }-sen(\theta )+\alpha \xi (t)$

Método de integração

Vamos montar um métodos para integrar o sistema no tempo. Primeiramente vamos dividir a equação em duas equações diferencias de primeira ordem, introduzindo a variável $\omega :=\dot{\theta }$, então ficamos com o seguinte sistema

$\begin{array}{rl}\dot{\theta }& =\omega \\ \dot{\omega }& =-2b\omega -sen(\theta )+\alpha \xi (t)\end{array}$

que pode ser escrito na forma diferencial

$\begin{array}{rl}d\theta & =\omega dt\\ d\omega & =(-2b\omega -sen(\theta ))dt+\alpha \xi (t)dt\end{array}$

mas $\xi (t)dt$ é o incremento do processo de Wiener ($W(t)=\underset{0}{\overset{t}{\int }}\xi (t^{\prime })d{t}^{\prime }$), então

$\begin{array}{rl}d\theta & =\omega dt\\ d\omega & =(-2b\omega -sen(\theta ))dt+\alpha dW(t)\end{array}$

Discretizando o tempo e lembrando que a densidade de probabilidade de transição de $W(t)$ para $W(t+\mathrm{\Delta }t)$ tem desvio padrão igual a $\sqrt{\mathrm{\Delta }t}$

$\begin{array}{rl}{\theta }_{j+1}& ={\theta }_j+{\omega }_j\mathrm{\Delta }t\\ {\omega }_{j+1}& ={\omega }_j+(-2b{\omega }_j-sen({\theta }_j))\mathrm{\Delta }t+\alpha {R_G}_j\sqrt{\mathrm{\Delta }t}\end{array}$

em que $R_G$ é uma amostra de uma distribuição gaussiana com média 0 e variância 1, e o método de Euler foi utilizado para a parte determinística da equação.

Nas próximas seções será analisado a energia do sistema, e como o método de Euler não é muito bom para preservar a energia de sistemas conservativos, será utilizado o método preditor corretor (com adição do método de Heun para $\theta$) para a parte determinística da equação, que consiste nos seguintes passos:

• Calcular um theta intermediário:

   ${\theta }_{j+1}^{(2)}={\theta }_j+{\omega }_j\mathrm{\Delta }t$

• Com ${\theta }_{j+1}^{(2)}$ calcular um theta médio e utilizá-lo para obter um omega intermediário:

   $\begin{array}{rl}{\overline{\theta }}_j& =\frac{{\theta }_{j+1}^{(2)}+{\theta }_j}{2}\\ {\omega }_{j+1}^{(2)}& ={\omega }_j+f({\overline{\theta }}_j,{\omega }_j,{R_G}_j)\end{array}$

Em que $f$ é a expressão do método de Euler visto logo acima.

• Recalcular theta utilizando um omega intermediário

   $\begin{array}{rl}{\overline{\omega }}_j& =\frac{{\omega }_{j+1}^{(2)}+{\omega }_j}{2}\\ {\theta }_{j+1}& ={\theta }_j+{\overline{\omega }}_j\mathrm{\Delta }t\end{array}$

• Recalcular omega com um theta intermediário atualizado

   $\begin{array}{rl}{\overline{\theta }}_j^{(2)}& =\frac{{\theta }_{j+1}+{\theta }_j}{2}\\ {\omega }_{j+1}& ={\omega }_j+f({\overline{\theta }}_j^{(2)},{\overline{\omega }}_j,{R_G}_j)\end{array}$

OBS: No cálculo de ${\omega }_{j+1}^{(2)}$ e ${\omega }_{j+1}$ foi utilizado o mesmo ${R_G}_j$.