Método Leapfrog: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 5: | Linha 5: | ||
<center><math> | <center><math> | ||
u_i^{n+1} = u_i^{n-1} + r (u_{i+1}^{n} - u_{i-1}^{n}) | u_i^{n+1} = u_i^{n-1} + r (u_{i+1}^{n} - u_{i-1}^{n}) | ||
</math></center> | </math></center> | ||
= Esquema de Matsuno = | = Esquema de Matsuno = | ||
| Linha 13: | Linha 13: | ||
<center><math> | <center><math> | ||
\frac{u_i^{(n+1)^*} - u_i^{n}}{\Delta t} = -v \frac{u_{i+1}^{n} - u_{i-1}^{n}}{2\Delta x} | \frac{u_i^{(n+1)^*} - u_i^{n}}{\Delta t} = -v \frac{u_{i+1}^{n} - u_{i-1}^{n}}{2\Delta x} | ||
</math></center> | </math></center> | ||
Assim, esses valores aproximados são empregados em um esquema atrasado, o qual | Assim, esses valores aproximados são empregados em um esquema atrasado, o qual | ||
| Linha 19: | Linha 19: | ||
<center><math> | <center><math> | ||
\frac{u_i^{n+1} - u_i^{n}}{\Delta t} = -v \frac{u_{i+1}^{(n+1)^*} - u_{i-1}^{(n+1)^*}}{2\Delta x} | \frac{u_i^{n+1} - u_i^{n}}{\Delta t} = -v \frac{u_{i+1}^{(n+1)^*} - u_{i-1}^{(n+1)^*}}{2\Delta x} | ||
</math></center> | </math></center> | ||
substituindo valores dados pelo esquema avançado, com o subscrito <math>i</math> substituído por <math>i+1</math>, temos: | substituindo valores dados pelo esquema avançado, com o subscrito <math>i</math> substituído por <math>i+1</math>, temos: | ||
| Linha 25: | Linha 25: | ||
<center><math> | <center><math> | ||
u_i^{n+1} = u_i^{n} - \frac{r}{2}(u_{i+1}^{n} - u_{i-1}^{n}) + \frac{r^2}{2}(u_{i+2}^{n} - u_{i}^{n} + u_{i-2}^{n}) | u_i^{n+1} = u_i^{n} - \frac{r}{2}(u_{i+1}^{n} - u_{i-1}^{n}) + \frac{r^2}{2}(u_{i+2}^{n} - u_{i}^{n} + u_{i-2}^{n}) | ||
</math></center> | </math></center> | ||
<source lang = "python"> | <source lang = "python"> | ||
Edição atual tal como às 19h45min de 5 de fevereiro de 2024
O termo "leapfrog" é utilizado devido aos níveis de tempo presentes na sua derivação, que superam os níveis de tempo no termo derivado do espaço. O método requer que e sejam armazenados para calcular .
Dessa forma, em relação à equação de advecção, temos:
Esquema de Matsuno
Primeiramente, os valores aproximados de serão calculados utilizando o esquema avançado, representado pela equação:
Assim, esses valores aproximados são empregados em um esquema atrasado, o qual
substituindo valores dados pelo esquema avançado, com o subscrito substituído por , temos:
# Solução pelo método Leapfrog para equação de advecção
def Leapfrogad(L, tf, v, Nx, Nt):
"""
Parâmetros:
- L: comprimento
- tf: tempo final
- v: velocidade de propagação
- Nx: número de pontos na direção espacial
- Nt: número de pontos na direção temporal
Retorna:
- Matriz com a solução da equação da onda
"""
dx = L / Nx
dt = tf / Nt
r = v * dt / dx
u = np.zeros((Nt, Nx+1))
# Condição inicial: u(x,0) = f(x)
x = np.linspace(0, L, Nx+1)
u[0, :] = 1 - np.cos(x) # Função que descreve a perturbação da onda
# Iteração no tempo
for n in range(0, Nt - 1):
for i in range(0, Nx+1):
# Condições de contorno
ip = i + 1 if i < Nx else 0 # índice i+1 (volta para 0 na borda)
ia = i - 1 if i > 0 else Nx # índice i-1 (volta para Nx na borda)
u[n+1, i] = u[n, i] + (r/2) * (u[n, ip] - u[n, ia]) - (r/2)**2 * (u[n, (ip+1) % (Nx + 1)] - u[n, i] + u[n, (ia-1) % (Nx + 1)])
return u
Ideia
- Se i é igual a Nx, então ip = Nx+1 e (ip+1) % (Nx + 1) se torna (Nx + 2) % (Nx + 1), que é equivalente a 0. Da mesma forma, se i é igual a 0, então ia = -1 e (ia-1) % (Nx + 1) se torna Nx;
- Quando i atinge o valor máximo Nx ou o valor mínimo 0, as expressões (ip+1) % (Nx + 1) e (ia-1) % (Nx + 1) garantem que os índices não ultrapassem os limites da matriz. O operador % (módulo) faz com que o índice retorne ao início (quando excede o limite superior) ou ao final (quando é menor que o limite inferior) da matriz.
# Parâmetros
L = 2*np.pi
tf =1
v = 1 # -1. muda direção de propagação
Nx = 100
Nt = 500
solv5 = Leapfrogad(L, tf, v, Nx, Nt)
listX = np.linspace(0, L, Nx+1)
listT = np.linspace(0, tf, Nt)
X, T = np.meshgrid(listX, listT)
plt.figure(figsize=(10, 6))
plt.pcolormesh(X, T, solv5, cmap='viridis', shading='auto')
plt.colorbar(label='Amplitude(u)')
plt.xlabel('Posição (x)')
plt.ylabel('Tempo (t)')
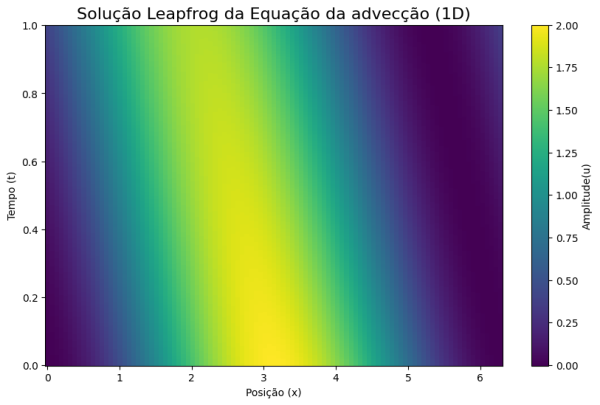
plt.title('Solução Leapfrog da Equação da advecção (1D)', fontsize=16)
plt.show()
# Teste: Plota todas as curvas amplitude por posição de todos os tempos:
for tt in range(len(listT-1)):
amplitudes_tt = solv5[ tt,:]
plt.plot(listX, amplitudes_tt)
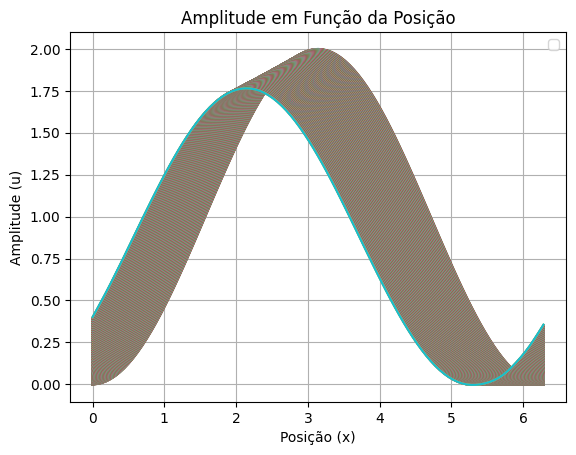
plt.title('Amplitude em Função da Posição')
plt.xlabel('Posição (x)')
plt.ylabel('Amplitude (u)')
plt.legend()
plt.grid(True)
plt.show()
Como é possível observar ele tem um efeito do amortecimento. Deste modo, o esquema do Matsuno não parece conveniente para resolver a equação da advecção, pois impõe um amortecimento na solução numérica, que não é observada na solução analítica. [Projeto PAE – Bolsista Simone E. Teleginski Ferraz. pg 5]