Equação de Cahn-Hilliard em 2D: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| (346 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Leonardo Dasso | '''Leonardo Dasso Migotto''' | ||
O objetivo deste trabalho é resolver computacionalmente a equação de Cahn-Hilliard | O objetivo deste trabalho é resolver computacionalmente a equação de Cahn-Hilliard utilizando a Transformada Rápida de Fourier <ref>https://fiscomp.if.ufrgs.br/index.php/FFT</ref> em uma e (principalmente) em duas dimensões. Será explorado as variações em concentração inicial e seus respectivos padrões formados, dados coeficientes de difusão e dimensões da superfície fixos. | ||
[[Arquivo: | [[Arquivo:NOPBC03.gif|thumb|Cahn-Hilliard bidimensional com condições de contorno periódicas.]] | ||
Esta equação já foi tratada em detalhes por colegas anteriores a mim <ref>https://fiscomp.if.ufrgs.br/index.php/Equa%C3%A7%C3%A3o_de_Cahn-Hilliard</ref>, | A equação de Cahn-Hilliard descreve a decomposição espinoidal<ref>CAHN, John W.; HILLIARD, John E. '''Spinodal decomposition: A reprise'''Acta Metallurgica, Volume 19, Issue 2, 1971</ref> em uma mistura binária, originando da primeira lei de Fick e a energia livre de Gibbs<ref>CAHN, John W.; HILLIARD, John E. '''Free Energy of a Nonuniform System. I. Interfacial Free Energy'''. The Journal of Chemical Physics, 1958.</ref>. Esta equação já foi tratada em detalhes por colegas anteriores a mim <ref>https://fiscomp.if.ufrgs.br/index.php/Equa%C3%A7%C3%A3o_de_Cahn-Hilliard</ref>, onde os aspectos físicos da equação são explicados em detalhes. Recomendo a leitura completa da página para melhor entendimento dos processos envolvidos na equação. O foco deste trabalho é explorar a solução numérica para a equação quando tratada em duas dimensões, onde a formação de padrões apresenta resultados mais interessantes. No entanto, a fim de facilitar a implementação e entendimento em duas dimensões, também será exibida uma implementação em uma dimensão. | ||
Todos | '''Todos códigos desenvolvidos para duas dimensões foram feitos a fim de que qualquer pessoa, com Python e as bibliotecas necessárias instaladas, possa executá-los sem nenhum conhecimento prévio. Estes códigos podem ser encontrados no final desta página.''' | ||
== Equação de Cahn-Hiliiard | == Equação de Cahn-Hiliiard Utilizando Transformada de Fourier == | ||
Para encontrar a equação que implementaremos com o uso da Transformada Rápida de Fourier, precisamos encontrar a nossa equação representada no espaço de Fourier. Seguirei a literatura de S. Bulent Biner <ref> | Para encontrar a equação que implementaremos com o uso da Transformada Rápida de Fourier, precisamos encontrar a nossa equação representada no espaço de Fourier. Seguirei a literatura de S. Bulent Biner <ref>BINER, S. Bulent. Programming Phase-Field Modeling. Idaho National Laboratory, Idaho Falls, ID, USA: Springer, 2017. 400 p. ISBN 978-3-319-41196-5.</ref>, onde há um capítulo dedicado a resolver equações de difusão com métodos desse tipo. Primeiro, resolveremos a equação em uma dimensão, que segue abaixo: | ||
:<math> | :<math> | ||
\frac{\partial c}{\partial t} = D {\nabla}^2 (c^3 - c - \gamma {\nabla}^2 c) | \frac{\partial c}{\partial t} = D {\nabla}^2 (c^3 - c - \gamma {\nabla}^2 c). | ||
</math> | </math> | ||
Lembrando que, conforme explicado no trabalho anterior a este, <math>c</math> é a soma da concentração de duas fases, e seu valor varia de -1 (presença de só uma das fases) a +1 (presença somente da outra fase), e <math>\gamma</math> é um valor relacionado à largura da interface das concentrações. | |||
Em uma dimensão, os laplacianos podem ser substituídos pela derivada segunda em relação a <math>x</math>, resultando na seguinte equação: | Em uma dimensão, os laplacianos podem ser substituídos pela derivada segunda em relação a <math>x</math>, resultando na seguinte equação: | ||
:<math> | :<math> | ||
\frac{\partial c}{\partial t} = D \Bigl( \frac{\partial^2 (c^3 - c)}{\partial x^2} - \gamma \frac{\partial^4 c}{\partial x^4} \Bigr) | \frac{\partial c}{\partial t} = D \Bigl( \frac{\partial^2 (c^3 - c)}{\partial x^2} - \gamma \frac{\partial^4 c}{\partial x^4} \Bigr). | ||
</math> | </math> | ||
| Linha 25: | Linha 27: | ||
:<math> | :<math> | ||
\frac{\partial \{c\}_k}{\partial t} = D \Bigl( \Bigl\{ \frac{ \partial^2 c^3 - c}{\partial x^2} \Bigr\}_k - \gamma \Bigl\{ \frac{\partial^4 c}{\partial x^4} \Bigr\}_k \Bigr) | \frac{\partial \{c\}_k}{\partial t} = D \Bigl( \Bigl\{ \frac{ \partial^2 c^3 - c}{\partial x^2} \Bigr\}_k - \gamma \Bigl\{ \frac{\partial^4 c}{\partial x^4} \Bigr\}_k \Bigr). | ||
</math> | </math> | ||
| Linha 31: | Linha 33: | ||
:<math> | :<math> | ||
\Bigl\{ \frac{\partial^n c}{\partial x^n} \Bigr\}_k \to (ik)^n \{c\}_k | \Bigl\{ \frac{\partial^n c}{\partial x^n} \Bigr\}_k \to (ik)^n \{c\}_k. | ||
</math> | </math> | ||
| Linha 37: | Linha 39: | ||
:<math> | :<math> | ||
\frac{\partial \{c\}_k}{\partial t} = D \bigl(-k^2 (\{c^3\}_k - \{c\}_k) - \gamma k^4 \{c\}_k \bigr) | \frac{\partial \{c\}_k}{\partial t} = D \bigl(-k^2 (\{c^3\}_k - \{c\}_k) - \gamma k^4 \{c\}_k \bigr). | ||
</math> | </math> | ||
O próximo passo é fazer a derivada à direita quanto ao tempo da seguinte maneira: | O próximo passo é fazer a derivada à direita quanto ao tempo, da seguinte maneira: | ||
:<math> | :<math> | ||
\frac{\partial \{c\}_k}{\partial t}\to \frac{\{c\}_k^{n+1}-\{c\}_k^n}{\Delta t} | \frac{\partial \{c\}_k}{\partial t}\to \frac{\{c\}_k^{n+1}-\{c\}_k^n}{\Delta t}. | ||
</math> | </math> | ||
| Linha 49: | Linha 51: | ||
:<math> | :<math> | ||
\{c\}_k^{n+1} = \{c\}_k^n + D \Delta t \bigl(-k^2 (\{c^3\}_k^n - \{c\}_k^n) - \gamma k^4 \{c\}_k^n \bigr) | \{c\}_k^{n+1} = \{c\}_k^n + D \Delta t \bigl(-k^2 (\{c^3\}_k^n - \{c\}_k^n) - \gamma k^4 \{c\}_k^n \bigr). | ||
</math> | </math> | ||
A equação que descobrimos para uma dimensão possui a mesma forma quando em duas dimensões. No entanto, <math>k</math> representará um vetor com coordenada <math>(k_{1}, k_{2})</math> com módulo <math>\sqrt{k_1^2 + k_2^2}</math>, onde <math>k_1</math> e <math>k_2</math> são os coeficientes em <math>x</math> e <math>y</math> respectivamente. | |||
== Código em | == Código em Uma Dimensão == | ||
O código completo está disponível no final desta página. Abaixo há o excerto da funcão, em Python, que calcula o instante seguinte do nosso sistema, utilizando as funções RFFT e IRFFT do pacote Scipy. | O código completo está disponível no final desta página. Abaixo há o excerto da funcão, em Python, que calcula o instante seguinte do nosso sistema, utilizando as funções RFFT e IRFFT do pacote Scipy. | ||
<source lang="python"> | <source lang="python"> | ||
| Linha 64: | Linha 66: | ||
return cc | return cc | ||
</source> | </source> | ||
No código, k2 e k4 são os coeficientes elevados às respectivas potências, | Gostaria de destacar que, para o uso correto do método, é necessário, para o termo cúbico, calcular a transformada '''após''' elevá-lo à potência, e não elevar o valor transformado à potência. No código, k2 e k4 são os coeficientes elevados às respectivas potências, além de que k4 está multiplicado pelo valor de <math>\gamma</math>. Calcular o quadrado de k2 e multiplica-lo por gamma fora da função evita que essas multiplicações sejam feito toda vez que a função é chamada. Também é importante destacar que as funções RFFT e IRFFT funcionam utilizando o vetor completo de pontos para fazer os cálculos, assim como os vetores completos de frequências, eliminando qualquer necessidade de iteração sobre o vetor de valores (uma diferença notável do método FTCS, onde é necessário iterar sobre o vetor). | ||
== Resultados em | == Resultados em Uma Dimensão e Discussão== | ||
Como já há um trabalho que trata em detalhes a implementação unidimensional e seus resultados, irei comparar aqui ambas implementações. Abaixo, vemos alguns instantes comparando ambos métodos a partir de uma condição inicial aleatória, utillizando condições de contorno periódicas, com o maior valor | Como já há um trabalho que trata em detalhes a implementação unidimensional e seus resultados, irei comparar aqui ambas implementações. Abaixo, vemos alguns instantes comparando ambos métodos (FTCS e por Transformadas de Fourier) a partir de uma condição inicial aleatória, utillizando condições de contorno periódicas, com o maior valor da diferença entre os dois métodos destacado no topo. O valor das constantes relevantes são: | ||
<math>\Delta t = \frac{1}{22 \cdot 10^{6}}, \Delta x = \frac{1}{128}, D = 1, \gamma = \Bigl(\frac{3.4}{128}\Bigr)^2, x_{max} = 1</math>. | |||
É interessante citar que a escolha de <math>\Delta x</math> como um valor tão específico não é em vão: a função RFFT utilizada no código apresenta maior rapidez de execução quando o vetor utilizado é de tamanho <math>2^n , n = 1, 2, 3, ...</math>. Com este valor de <math>\Delta x</math>, nosso vetor é composto de 128 elementos, ou <math>2^7</math> elementos, fazendo uso dessa vantagem. | |||
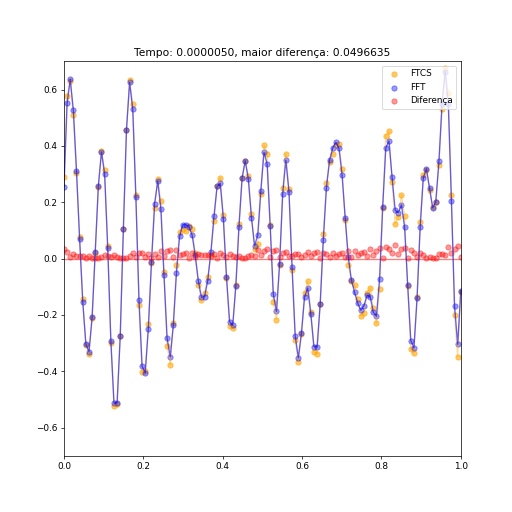
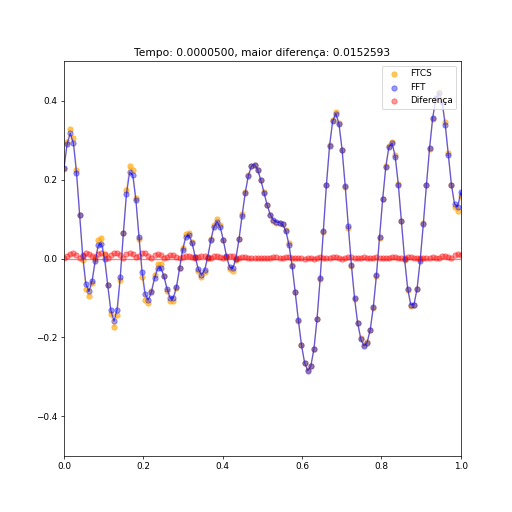
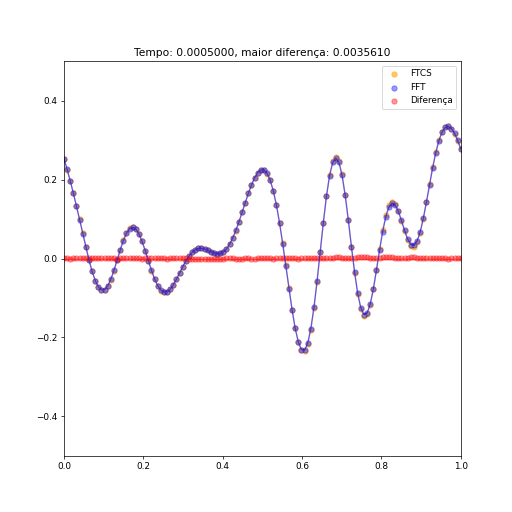
[[Arquivo:1d100passos.png]] [[Arquivo:1d1000passos.png]] [[Arquivo:1d10000.png]] | [[Arquivo:1d100passos.png]] [[Arquivo:1d1000passos.png]] [[Arquivo:1d10000.png]] | ||
Como podemos ver, a diferença dos valores entre os resultados obtidos pelo método FTCS e o método das transformadas é | Repare na mudança de limites no eixo vertical dos gráficos, a fim de ressaltar a posição dos valores maiores da diferença. Como podemos ver, a diferença dos valores entre os resultados obtidos pelo método FTCS e o método das transformadas é pequena (após poucos instantes o maior módulo da diferença aproxima-se de 0,01). A fim de avaliar com maior precisão a diferença entre ambos métodos, quatro pontos foram escolhidos ao acaso, e a diferença de valor entre ambos métodos sob cada ponto foram graficadas, e podem ser vistas abaixo. | ||
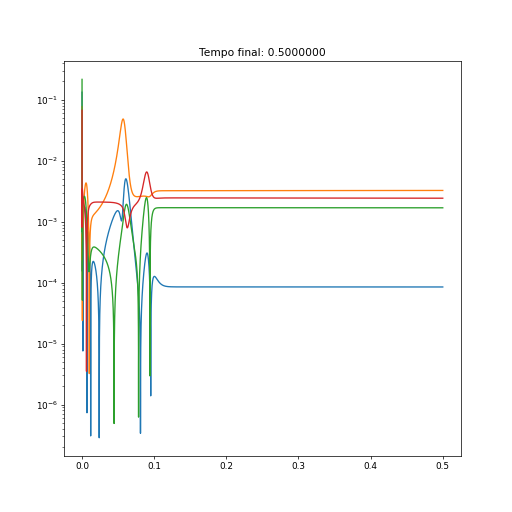
[[Arquivo:diferencalog.png]] | |||
No gráfico acima, vemos que a diferença entre os valores varia erráticamente até logo após um tempo de 0.1. Repare que, logo em seguida, a diferença entre os pontos estabiliza em um certo valor. O comportamento do erro torna evidente que a diferença numérica entre ambos métodos se dá principalmente nos instantes iniciais, enquanto as concentrações aleatórias estão começando o processo de difusão. A estabilização da diferença indica que ambos métodos, para tempos mais longos, possuem diferença numérica mínima, somente preservando a diferença obtida no tempo inicial. | |||
É interessante citar que a escolha de <math>\Delta x</math> como um valor tão específico não é em vão: a função RFFT utilizada no código apresenta maior rapidez de execução quando o vetor utilizado é de tamanho <math>2^n , n = 1, 2, 3, ...</math>. Com este valor de <math>\Delta x</math>, nosso vetor é composto de 128 elementos, ou <math>2^7</math> elementos, fazendo uso dessa vantagem. Dado a escala utilizada no sistema acima, os tempos de processamento foram pequenos. No entanto, para sistemas maiores (como o bidimensional), onde o número de operações necessárias aumenta drasticamente, o método das transformadas será distintamente ágil. | |||
== Código em | == Código em Duas Dimensões == | ||
Todos códigos estão disponíveis na íntegra no final desta página. A fim de poupar tempo, quatro programas foram criados: | Todos códigos estão disponíveis na íntegra no final desta página. A fim de poupar tempo, quatro programas foram criados: | ||
:- Um programa que gera, a partir de valores aleatórios parametrizados, | :- Um programa que gera, a partir de valores aleatórios parametrizados, dados até um certo instante de tempo, salvando-os em um arquivo. | ||
:- Um programa que, lê um arquivo de valores já gerados e gera mais valores até um certo instante de tempo, salvando-os neste mesmo arquivo. | :- Um programa que, lê um arquivo de valores já gerados e gera mais valores até um certo instante de tempo, salvando-os neste mesmo arquivo. | ||
:- Um programa que lê um arquivo gerado | :- Um programa que lê um arquivo gerado previamente, criando frames dos valores salvos no arquivo. | ||
:- Um programa que lê um arquivo gerado | :- Um programa que lê um arquivo gerado previamente, criando uma animação dos valores salvos no arquivo. | ||
Dois arquivos de formato .npy são criados, para armazenar os arrays e as informações necessárias para gerar mais valores ou plotar os gráficos, além de um .txt que serve como uma consulta local dos valores pelo usuário (arquivos .npy não podem ser lidos no bloco de notas). Todos arquivos são salvos em pastas individuias cujo nome é um número aleatório único, sendo este número o nome do arquivo de texto, o do arquivo .npy e o arquivo com os valores calculados. | |||
Abaixo há o excerto da funcão, em Python, que calcula o instante seguinte do nosso sistema, utilizando as funções RFFT2 e IRFFT2 do pacote Scipy. | Abaixo há o excerto da funcão, em Python, que calcula o instante seguinte do nosso sistema, utilizando as funções RFFT2 e IRFFT2 do pacote Scipy. | ||
<source lang="python"> | <source lang="python"> | ||
| Linha 90: | Linha 102: | ||
return ccn | return ccn | ||
</source> | </source> | ||
No código, kk2 e kk4 são os coeficientes elevados às respectivas potências, | No código, kk2 e kk4 são os coeficientes elevados às respectivas potências, além de que k4 está multiplicado pelo valor de <math>\gamma</math>. Vale destacar a semelhança entre este código e o unidimensional, fruto da discretização quase idêntica. | ||
== Resultado em Duas Dimensões: Concentração Média 0 == | |||
Para todos resultados abaixo, foram utilizados as seguintes constantes relevantes: | |||
<math>\Delta t = \frac{1.8}{10^7}, \Delta x = \Delta y = \frac{1}{128}, D = 1, \gamma = 0.01^2, x_{max} = 1</math>. | |||
Também foram utilizadas condições de contorno periódicas. Como observado anteriormente, o valor de <math>\Delta x</math> escolhido serve para que nosso array de valores possua <math>10^{14}</math> elementos, também fazendo uso da eficiência completa da função RFFT2 (equivalente bidimensional da função RFFT). | |||
O motivo de não explorarmos valores diferentes de <math>\gamma</math> nem de <math>D</math> está na sensibilidade da estabilidade da equação: pequenas mudanças na ordem de grandeza de qualquer uma das constantes pode resultar num sistema instável. | |||
Segue abaixo mídias da difusão sob estes parâmetros com concentração média 0. As cores variam de vermelho (-1) a violeta (+1), de modo que as cores variam de acordo com o espectro visível, onde a cor amarela corresponde a 0. A "baixa qualidade" das imagens se dá pelo tamanho de array utilizado (128x128), de modo que cada célula é distintamente visível nas mídias. Mesmo "pequeno", o tamanho de array escolhido já permite a análise dos dados, além de ter um tempo de processamento rápido. | |||
[[Arquivo: NOPBCINICIAL.png|thumb|none|256px|Instante inicial com concentrações aleatórias.]] | |||
[[Arquivo: PBC BEM CEDO1.png|thumb|none|384px|Instante expandido a fim de demonstrar as condições de contorno periódicas. Esta imagem é composta por uma grade 3x3 de imagens iguais das de tamanho menor, dando origem a uma imagem de resolução 384x384.]] | |||
[[Arquivo: FINALDOGIF1.png|frame|left|256px|Tempo: 0.011. Repare na rápida formação das fases.]][[Arquivo: NOPBCCURTO.gif|frame|center|256px|Tempo máximo da animação: 0.011.]] | |||
[[Arquivo: FINALDOGIF2.png|frame|left|256px|Tempo: 0.3.]][[Arquivo: NOPBC03.gif|frame|center|256px|Tempo máximo da animação: 0.3. Este vídeo está acelerado em relação ao anterior. Repare na difusão das "bolhas" que não entraram em contato com outras concentrações. Repare que as outras concentrações crescem de tamanho conforme a bolha "difunde" no meio.]] | |||
[[Arquivo: FINALDOGIF3.png|frame|left|256px|Tempo: 3. Repare no arredondamento da concentração singular que se formou.]] [[Arquivo: NOPBC3NOVO.gif|frame|center|256px|Tempo máximo da animação: 3. Este vídeo está acelerado em relação ao anterior.]] | |||
[[Arquivo: PBCFINAL5050.png|frame|none|384px|Tempo: 6. Aqui, as fases já atingiram a estabilidade. Utilizando da visualização expandida, podemos ver que uma das fases formou uma concentração circular, enquanto a outra ocupou o espaço remanescente.]] [[Arquivo: MOSTRANDO ESTABILIDADE.gif|frame|none|512px|Tempo máximo da animação: 6. Este vídeo está acelerado em relação ao anterior.]] | |||
== Resultado em Duas Dimensões: Concentração Média 0.5 == | |||
Abaixo seguem mídias da simulação de condições iniciais idênticas às anteriores, porém com concentração média inicial 0.5 (equivalente a 75% em uma fase e 25% em outra). | |||
[[Arquivo: FRAMEINICIAL.png|thumb|none|256px|Instante inicial com concentrações aleatórias. Repare nas cores serem majoritariamente verdes ou azuis, relativas à concentrações de valor positivo.]] | |||
[[Arquivo: DESTAQUEPBC.png|thumb|none|384px|Instante expandido a fim de demonstrar as condições de contorno periódicas. Esta imagem é composta por uma grade 3x3 de imagens iguais das de tamanho menor, dando origem a uma imagem de resolução 384x384.]] | |||
[[Arquivo: FRAMENOVO10.png|frame|left|256px|Tempo: 0.010. Repare na rápida formação de concentrações pequenas da fase em minoria.]] [[Arquivo: TEMPOCURTO.gif|frame|center|256px|Tempo máximo da animação: 0.010.]] | |||
[[Arquivo: FRAMENOVO11.png|frame|left|256px|Tempo: 0.3. Repare na homogenização da fase em maior quantidade.]] [[Arquivo: TMAX03.gif|frame|center|256px|Tempo máximo da animação: 0.3. Este vídeo está acelerado em relação ao anterior. Repare na difusão das "bolhas" que não entraram em contato com outras concentrações.]] | |||
[[Arquivo: FRAMENOVO12.png|frame|left|256px|Tempo: 3. Repare na formação de 3 concentrações já circulares de forma.]] [[Arquivo: TMAX3.gif|frame|center|256px|Tempo máximo da animação: 3. Este vídeo está acelerado em relação ao anterior. Repare no início da difusão de uma das concentrações.]] | |||
[[Arquivo: FINALPEQUENOCONC.png|thumb|none|384px|Tempo: 7. As fases já atingiram a estabilidade.]] | |||
[[Arquivo:GIFINAL GRANDE.gif|frame|none|512px|Tempo máximo da animação: 7. Este vídeo está acelerado em relação ao anterior.]] | |||
== Discussão dos resultados em duas dimensões== | == Discussão dos resultados em duas dimensões== | ||
Dado que, utilizando valores aleatórios, nosso sistema é equivalente a uma mistura homogênea com perturbações, percebemos instantaneamente a formação das regiões das diferentes fases. | |||
Após poucos instantes, já percebemos a separação completa das fases, com exceção das fronteiras, que apresentam uma mistura de ambas. É importante destacar que, conforme maiores as concentrações de fases se tornam, menor a velocidade que elas se "movem". Ao lembrar que a equação de Cahn-Hilliard descreve a separação de fases em um sistema homogêneo termodiamicamente instável, que reduz sua energia conforme a separação delas, fica evidente que a desaçeleração da separação ocorre pela aproximação da sua energia atual à energia mínima do sistema. A redução da energia com o tempo pode ser visto no livro de S. Bulent Biner. | |||
Também percebemos que concentrações menores difundiam, quando não entravam em contato com outra concentração maior. Mesmo aparentando, em alguns momentos, desaparecer, na realidade a área das outras concentrações aumenta, de modo que a quantidade de cada fase se mantem igual. | |||
Percebemos que o estado de menor energia é uma concentração circular, enquanto o restante do meio é ocupado pela outra. Mesmo sem saber que este é o estado estacionário, poderíamos intuir que seria ele ao ver os instantes iniciais da simulação: o círculo é a forma que possui maior área por perímetro, e vimos que as fases diferentes difundem de modo a diminuir sua interface. No caso de uma quantidade diferente entre as fases, a de menor volume (ou neste caso, área) total, forma o círculo, caso contrário, a concentração que forma é escolhida "aleatoriamente" (depende dos locais das perturbações, que, no nosso caso, são aleatórias). O motivo de ambas fases poderem formar a concentração circular é o fato da equação possuir todos termos de expoente ímpar, de modo que valores positivos ou negativos são tradados da mesma maneira (ao contrário de termos com expoente par, que retornam um valor positivo independente do sinal, agindo de forma diferente dependendo do sinal do valor original). | |||
== Códigos == | |||
Todos códigos para resolução numérica em duas dimensões possuem, nas primeiras linhas, comentários que destacam quais valores o usuário é recomendado a alterar, além da semente aleatória utilizada para gerar as mídias vistas na página. Caso você não possua experiência com programação, é recomendado não alterar as linhas de código abaixo dos locais indicados. | |||
:'''[[cahn2dfourier]]''' Programa utilizado para gerar valores sem partir de nenhum arquivo anterior. Os dados são identificados por um código numérico único, e serão salvos em uma pasta com nome de tal código, onde ali se encontrarão: | |||
:- O arquivo código.npy principal, que consiste nos arrays. | |||
:- O arquivo valcódigo.npy, que consiste em um arquivo que é lido pelos outros programas contendo informações cruciais. | |||
:- O arquivo código.txt, que contém tais informações cruciais em um formato legível ao usuário. | |||
Utilizado em conjunto com os programas "framer" e "animador", você pode gerar imagens como as vistas neste trabalho. | |||
:'''[[cahn2dfouriercontinue]]''' Programa utilizado para gerar valores partindo de outros já antes calculados. O arquivo com os dados novos (concatenados aos antigos) se encontrará na pasta original, substituindo o arquivo antigo. Recomendado para gerar valores por tempos longos sem precisar deixar o programa executando por longas horas sem intervalo. | |||
:'''[[cahn2dframer]]''' Programa utilizado para gerar as imagens estáticas vistas neste trabalho. Ele salvará os frames em uma pasta dentro da pasta com nome do código do arquivo, e serão numerados de acordo com qual frame da simulação ela se refere. | |||
:'''[[cahn2danimador]]''' Programa utilizado para gerar as animações vistas neste trabalho. Os gifs são salvos em uma pasta dentro da pasta com nome do código do arquivo, com o nome dele identificando algumas características dele. Atente que, para computadores sem placa de vídeo dedicada, a renderização dos gifs pode levar muito tempo, em casos como este recomendo gerar as animações em menor resolução ou com intervalos maiores entre as imagens. | |||
:'''[[cahn1dcompare]]''' Código utilizado para gerar o frame de comparação em uma dimensão. Não recomendo acessá-lo, por não possuir um resultado interessante, além de não estar otimizado nem comentado. | |||
:'''[[cahn1ddiflog]]''' Código utilizado para avaliar a diferença entre os métodos em escala logarítmica. Não recomendo acessá-lo, por não possuir um resultado interessante, além de não estar otimizado nem comentado. | |||
'''As bibliotecas utilizadas que requerem instalação são: Numpy, Scipy e Matplotlib. O renderizador de vídeo FFMPEG foi utilizado, porém na maioria dos computadores modernos executando Windows, na ausência deste, outro renderizador será utilizado sem necessidade de alterar o código. Porém, caso seja necessário instalar o renderizador, este link possui um tutorial simples em inglês para Windows: [https://stackoverflow.com/posts/65860115/revisions]''' | |||
== Referências == | == Referências == | ||
<references/> | <references/> | ||
Edição atual tal como às 16h14min de 22 de julho de 2024
Leonardo Dasso Migotto
O objetivo deste trabalho é resolver computacionalmente a equação de Cahn-Hilliard utilizando a Transformada Rápida de Fourier [1] em uma e (principalmente) em duas dimensões. Será explorado as variações em concentração inicial e seus respectivos padrões formados, dados coeficientes de difusão e dimensões da superfície fixos.
A equação de Cahn-Hilliard descreve a decomposição espinoidal[2] em uma mistura binária, originando da primeira lei de Fick e a energia livre de Gibbs[3]. Esta equação já foi tratada em detalhes por colegas anteriores a mim [4], onde os aspectos físicos da equação são explicados em detalhes. Recomendo a leitura completa da página para melhor entendimento dos processos envolvidos na equação. O foco deste trabalho é explorar a solução numérica para a equação quando tratada em duas dimensões, onde a formação de padrões apresenta resultados mais interessantes. No entanto, a fim de facilitar a implementação e entendimento em duas dimensões, também será exibida uma implementação em uma dimensão.
Todos códigos desenvolvidos para duas dimensões foram feitos a fim de que qualquer pessoa, com Python e as bibliotecas necessárias instaladas, possa executá-los sem nenhum conhecimento prévio. Estes códigos podem ser encontrados no final desta página.
Equação de Cahn-Hiliiard Utilizando Transformada de Fourier
Para encontrar a equação que implementaremos com o uso da Transformada Rápida de Fourier, precisamos encontrar a nossa equação representada no espaço de Fourier. Seguirei a literatura de S. Bulent Biner [5], onde há um capítulo dedicado a resolver equações de difusão com métodos desse tipo. Primeiro, resolveremos a equação em uma dimensão, que segue abaixo:
Lembrando que, conforme explicado no trabalho anterior a este, é a soma da concentração de duas fases, e seu valor varia de -1 (presença de só uma das fases) a +1 (presença somente da outra fase), e é um valor relacionado à largura da interface das concentrações.
Em uma dimensão, os laplacianos podem ser substituídos pela derivada segunda em relação a , resultando na seguinte equação:
Para solucioná-la numericamente, aplicaremos a Transformada de Fourier à frente em ambos os lados, da maneira descrita abaixo, onde k é o respectivo coeficiente de Fourier):
Em seguida, substituimos as derivadas espaciais pela sua equivalente no espaço de Fourier:
Assim, obtemos a seguinte equação:
O próximo passo é fazer a derivada à direita quanto ao tempo, da seguinte maneira:
Substituindo na equação e reescrevendo-a a fim de isolar , obtemos a equação final:
A equação que descobrimos para uma dimensão possui a mesma forma quando em duas dimensões. No entanto, representará um vetor com coordenada com módulo , onde e são os coeficientes em e respectivamente.
Código em Uma Dimensão
O código completo está disponível no final desta página. Abaixo há o excerto da funcão, em Python, que calcula o instante seguinte do nosso sistema, utilizando as funções RFFT e IRFFT do pacote Scipy.
def cahnfourier1d(cc, k2, k4):
cct = rfft(cc)
cct3 = rfft(cc**3 - cc)
cct = cct + difd*dt*(-k2*(cct3) - k4*cct)
cc = irfft(cct)
return cc
Gostaria de destacar que, para o uso correto do método, é necessário, para o termo cúbico, calcular a transformada após elevá-lo à potência, e não elevar o valor transformado à potência. No código, k2 e k4 são os coeficientes elevados às respectivas potências, além de que k4 está multiplicado pelo valor de . Calcular o quadrado de k2 e multiplica-lo por gamma fora da função evita que essas multiplicações sejam feito toda vez que a função é chamada. Também é importante destacar que as funções RFFT e IRFFT funcionam utilizando o vetor completo de pontos para fazer os cálculos, assim como os vetores completos de frequências, eliminando qualquer necessidade de iteração sobre o vetor de valores (uma diferença notável do método FTCS, onde é necessário iterar sobre o vetor).
Resultados em Uma Dimensão e Discussão
Como já há um trabalho que trata em detalhes a implementação unidimensional e seus resultados, irei comparar aqui ambas implementações. Abaixo, vemos alguns instantes comparando ambos métodos (FTCS e por Transformadas de Fourier) a partir de uma condição inicial aleatória, utillizando condições de contorno periódicas, com o maior valor da diferença entre os dois métodos destacado no topo. O valor das constantes relevantes são:
.
É interessante citar que a escolha de como um valor tão específico não é em vão: a função RFFT utilizada no código apresenta maior rapidez de execução quando o vetor utilizado é de tamanho . Com este valor de , nosso vetor é composto de 128 elementos, ou elementos, fazendo uso dessa vantagem.
Repare na mudança de limites no eixo vertical dos gráficos, a fim de ressaltar a posição dos valores maiores da diferença. Como podemos ver, a diferença dos valores entre os resultados obtidos pelo método FTCS e o método das transformadas é pequena (após poucos instantes o maior módulo da diferença aproxima-se de 0,01). A fim de avaliar com maior precisão a diferença entre ambos métodos, quatro pontos foram escolhidos ao acaso, e a diferença de valor entre ambos métodos sob cada ponto foram graficadas, e podem ser vistas abaixo.
No gráfico acima, vemos que a diferença entre os valores varia erráticamente até logo após um tempo de 0.1. Repare que, logo em seguida, a diferença entre os pontos estabiliza em um certo valor. O comportamento do erro torna evidente que a diferença numérica entre ambos métodos se dá principalmente nos instantes iniciais, enquanto as concentrações aleatórias estão começando o processo de difusão. A estabilização da diferença indica que ambos métodos, para tempos mais longos, possuem diferença numérica mínima, somente preservando a diferença obtida no tempo inicial.
É interessante citar que a escolha de como um valor tão específico não é em vão: a função RFFT utilizada no código apresenta maior rapidez de execução quando o vetor utilizado é de tamanho . Com este valor de , nosso vetor é composto de 128 elementos, ou elementos, fazendo uso dessa vantagem. Dado a escala utilizada no sistema acima, os tempos de processamento foram pequenos. No entanto, para sistemas maiores (como o bidimensional), onde o número de operações necessárias aumenta drasticamente, o método das transformadas será distintamente ágil.
Código em Duas Dimensões
Todos códigos estão disponíveis na íntegra no final desta página. A fim de poupar tempo, quatro programas foram criados:
- - Um programa que gera, a partir de valores aleatórios parametrizados, dados até um certo instante de tempo, salvando-os em um arquivo.
- - Um programa que, lê um arquivo de valores já gerados e gera mais valores até um certo instante de tempo, salvando-os neste mesmo arquivo.
- - Um programa que lê um arquivo gerado previamente, criando frames dos valores salvos no arquivo.
- - Um programa que lê um arquivo gerado previamente, criando uma animação dos valores salvos no arquivo.
Dois arquivos de formato .npy são criados, para armazenar os arrays e as informações necessárias para gerar mais valores ou plotar os gráficos, além de um .txt que serve como uma consulta local dos valores pelo usuário (arquivos .npy não podem ser lidos no bloco de notas). Todos arquivos são salvos em pastas individuias cujo nome é um número aleatório único, sendo este número o nome do arquivo de texto, o do arquivo .npy e o arquivo com os valores calculados. Abaixo há o excerto da funcão, em Python, que calcula o instante seguinte do nosso sistema, utilizando as funções RFFT2 e IRFFT2 do pacote Scipy.
def cahnfourier2d(aa, kk2, kk4):
cct = rfft2(aa)
cct3 = rfft2(aa**3)
cct = cct + difd*dt*(-kk2*(cct3 - cct) - kk4*cct)
ccn = irfft2(cct)
return ccn
No código, kk2 e kk4 são os coeficientes elevados às respectivas potências, além de que k4 está multiplicado pelo valor de . Vale destacar a semelhança entre este código e o unidimensional, fruto da discretização quase idêntica.
Resultado em Duas Dimensões: Concentração Média 0
Para todos resultados abaixo, foram utilizados as seguintes constantes relevantes:
.
Também foram utilizadas condições de contorno periódicas. Como observado anteriormente, o valor de escolhido serve para que nosso array de valores possua elementos, também fazendo uso da eficiência completa da função RFFT2 (equivalente bidimensional da função RFFT).
O motivo de não explorarmos valores diferentes de nem de está na sensibilidade da estabilidade da equação: pequenas mudanças na ordem de grandeza de qualquer uma das constantes pode resultar num sistema instável.
Segue abaixo mídias da difusão sob estes parâmetros com concentração média 0. As cores variam de vermelho (-1) a violeta (+1), de modo que as cores variam de acordo com o espectro visível, onde a cor amarela corresponde a 0. A "baixa qualidade" das imagens se dá pelo tamanho de array utilizado (128x128), de modo que cada célula é distintamente visível nas mídias. Mesmo "pequeno", o tamanho de array escolhido já permite a análise dos dados, além de ter um tempo de processamento rápido.
Resultado em Duas Dimensões: Concentração Média 0.5
Abaixo seguem mídias da simulação de condições iniciais idênticas às anteriores, porém com concentração média inicial 0.5 (equivalente a 75% em uma fase e 25% em outra).
Discussão dos resultados em duas dimensões
Dado que, utilizando valores aleatórios, nosso sistema é equivalente a uma mistura homogênea com perturbações, percebemos instantaneamente a formação das regiões das diferentes fases.
Após poucos instantes, já percebemos a separação completa das fases, com exceção das fronteiras, que apresentam uma mistura de ambas. É importante destacar que, conforme maiores as concentrações de fases se tornam, menor a velocidade que elas se "movem". Ao lembrar que a equação de Cahn-Hilliard descreve a separação de fases em um sistema homogêneo termodiamicamente instável, que reduz sua energia conforme a separação delas, fica evidente que a desaçeleração da separação ocorre pela aproximação da sua energia atual à energia mínima do sistema. A redução da energia com o tempo pode ser visto no livro de S. Bulent Biner.
Também percebemos que concentrações menores difundiam, quando não entravam em contato com outra concentração maior. Mesmo aparentando, em alguns momentos, desaparecer, na realidade a área das outras concentrações aumenta, de modo que a quantidade de cada fase se mantem igual.
Percebemos que o estado de menor energia é uma concentração circular, enquanto o restante do meio é ocupado pela outra. Mesmo sem saber que este é o estado estacionário, poderíamos intuir que seria ele ao ver os instantes iniciais da simulação: o círculo é a forma que possui maior área por perímetro, e vimos que as fases diferentes difundem de modo a diminuir sua interface. No caso de uma quantidade diferente entre as fases, a de menor volume (ou neste caso, área) total, forma o círculo, caso contrário, a concentração que forma é escolhida "aleatoriamente" (depende dos locais das perturbações, que, no nosso caso, são aleatórias). O motivo de ambas fases poderem formar a concentração circular é o fato da equação possuir todos termos de expoente ímpar, de modo que valores positivos ou negativos são tradados da mesma maneira (ao contrário de termos com expoente par, que retornam um valor positivo independente do sinal, agindo de forma diferente dependendo do sinal do valor original).
Códigos
Todos códigos para resolução numérica em duas dimensões possuem, nas primeiras linhas, comentários que destacam quais valores o usuário é recomendado a alterar, além da semente aleatória utilizada para gerar as mídias vistas na página. Caso você não possua experiência com programação, é recomendado não alterar as linhas de código abaixo dos locais indicados.
- cahn2dfourier Programa utilizado para gerar valores sem partir de nenhum arquivo anterior. Os dados são identificados por um código numérico único, e serão salvos em uma pasta com nome de tal código, onde ali se encontrarão:
- - O arquivo código.npy principal, que consiste nos arrays.
- - O arquivo valcódigo.npy, que consiste em um arquivo que é lido pelos outros programas contendo informações cruciais.
- - O arquivo código.txt, que contém tais informações cruciais em um formato legível ao usuário.
Utilizado em conjunto com os programas "framer" e "animador", você pode gerar imagens como as vistas neste trabalho.
- cahn2dfouriercontinue Programa utilizado para gerar valores partindo de outros já antes calculados. O arquivo com os dados novos (concatenados aos antigos) se encontrará na pasta original, substituindo o arquivo antigo. Recomendado para gerar valores por tempos longos sem precisar deixar o programa executando por longas horas sem intervalo.
- cahn2dframer Programa utilizado para gerar as imagens estáticas vistas neste trabalho. Ele salvará os frames em uma pasta dentro da pasta com nome do código do arquivo, e serão numerados de acordo com qual frame da simulação ela se refere.
- cahn2danimador Programa utilizado para gerar as animações vistas neste trabalho. Os gifs são salvos em uma pasta dentro da pasta com nome do código do arquivo, com o nome dele identificando algumas características dele. Atente que, para computadores sem placa de vídeo dedicada, a renderização dos gifs pode levar muito tempo, em casos como este recomendo gerar as animações em menor resolução ou com intervalos maiores entre as imagens.
- cahn1dcompare Código utilizado para gerar o frame de comparação em uma dimensão. Não recomendo acessá-lo, por não possuir um resultado interessante, além de não estar otimizado nem comentado.
- cahn1ddiflog Código utilizado para avaliar a diferença entre os métodos em escala logarítmica. Não recomendo acessá-lo, por não possuir um resultado interessante, além de não estar otimizado nem comentado.
As bibliotecas utilizadas que requerem instalação são: Numpy, Scipy e Matplotlib. O renderizador de vídeo FFMPEG foi utilizado, porém na maioria dos computadores modernos executando Windows, na ausência deste, outro renderizador será utilizado sem necessidade de alterar o código. Porém, caso seja necessário instalar o renderizador, este link possui um tutorial simples em inglês para Windows: [1]
Referências
- ↑ https://fiscomp.if.ufrgs.br/index.php/FFT
- ↑ CAHN, John W.; HILLIARD, John E. Spinodal decomposition: A repriseActa Metallurgica, Volume 19, Issue 2, 1971
- ↑ CAHN, John W.; HILLIARD, John E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. The Journal of Chemical Physics, 1958.
- ↑ https://fiscomp.if.ufrgs.br/index.php/Equa%C3%A7%C3%A3o_de_Cahn-Hilliard
- ↑ BINER, S. Bulent. Programming Phase-Field Modeling. Idaho National Laboratory, Idaho Falls, ID, USA: Springer, 2017. 400 p. ISBN 978-3-319-41196-5.